Предисловие
Совсем недавно в этом блоге была опубликована статья, посвященная алгоритму поведения роя пчел. Данная статья рассказывает о другом алгоритме роевого интеллекта, называемом муравьиным алгоритмом. Она состоит из введения, вкратце рассказывающего о заимствованном природном механизме, описания оригинального алгоритма Марко Дориго, обзора других муравьиных алгоритмов и заключения, в котором указываются области применения муравьиных алгоритмов и перспективные направления в их исследованиях.
Введение
Муравья нельзя назвать сообразительным. Отдельный муравей не в состоянии принять ни малейшего решения. Дело в том, что он устроен крайне примитивно: все его действия сводятся к элементарным реакциям на окружающую обстановку и своих собратьев. Муравей не способен анализировать, делать выводы и искать решения.
Эти факты, однако, никак не согласуются с успешностью муравьев как вида. Они существуют на планете более 100 миллионов лет, строят огромные жилища, обеспечивают их всем необходимым и даже ведут настоящие войны. В сравнении с полной беспомощностью отдельных особей, достижения муравьев кажутся немыслимыми.
Добиться таких успехов муравьи способны благодаря своей социальности. Они живут только в коллективах – колониях. Все муравьи колонии формируют так называемый роевой интеллект. Особи, составляющие колонию, не должны быть умными: они должны лишь взаимодействовать по определенным – крайне простым – правилам, и тогда колония целиком будет эффективна.
В колонии нет доминирующих особей, нет начальников и подчиненных, нет лидеров, которые раздают указания и координируют действия. Колония является полностью самоорганизующейся. Каждый из муравьев обладает информацией только о локальной обстановке, не один из них не имеет представления обо всей ситуации в целом – только о том, что узнал сам или от своих сородичей, явно или неявно. На неявных взаимодействиях муравьев, называемых стигмергией, основаны механизмы поиска кратчайшего пути от муравейника до источника пищи.
Каждый раз проходя от муравейника до пищи и обратно, муравьи оставляют за собой дорожку феромонов. Другие муравьи, почувствовав такие следы на земле, будут инстинктивно устремляться к нему. Поскольку эти муравьи тоже оставляют за собой дорожки феромонов, то чем больше муравьев проходит по определенному пути, тем более привлекательным он становится для их сородичей. При этом, чем короче путь до источника пищи, тем меньше времени требуется муравьям на него – а следовательно, тем быстрее оставленные на нем следы становятся заметными.
В 1992 году в своей диссертации Марко Дориго (Marco Dorigo) предложил заимствовать описанный природный механизм для решения задач оптимизации [1]. Имитируя поведение колонии муравьев в природе, муравьиные алгоритмы используют многоагентные системы, агенты которых функционируют по крайне простым правилам. Они крайне эффективны при решении сложных комбинаторных задач – таких, например, как задача коммивояжера, первая из решенных с использованием данного типа алгоритмов.
Классический муравьиный алгоритм для решения задачи коммивояжера
Как было сказано выше, муравьиный алгоритм моделирует многоагентную систему. Ее агентов в дальнейшем будем называть муравьями. Как и настоящие муравьи, они довольно просто устроены: для выполнения своих обязанностей они требуют небольшое количество памяти, а на каждом шаге работы выполняют несложные вычисления.
Каждый муравей хранит в памяти список пройденных им узлов. Этот список называют списком запретов (tabu list) или просто памятью муравья. Выбирая узел для следующего шага, муравей «помнит» об уже пройденных узлах и не рассматривает их в качестве возможных для перехода. На каждом шаге список запретов пополняется новым узлом, а перед новой итерацией алгоритма – то есть перед тем, как муравей вновь проходит путь – он опустошается.
Кроме списка запретов, при выборе узла для перехода муравей руководствуется «привлекательностью» ребер, которые он может пройти. Она зависит, во-первых, от расстояния между узлами (то есть от веса ребра), а во-вторых, от следов феромонов, оставленных на ребре прошедшими по нему ранее муравьями. Естественно, что в отличие от весов ребер, которые являются константными, следы феромонов обновляются на каждой итерации алгоритма: как и в природе, со временем следы испаряются, а проходящие муравьи, напротив, усиливают их.
Пусть муравей находится в узле
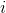 , а узел
, а узел 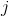 – это один из узлов, доступных для перехода:
– это один из узлов, доступных для перехода:  . Обозначим вес ребра, соединяющего узлы
. Обозначим вес ребра, соединяющего узлы 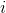 и
и 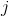 , как
, как  , а интенсивность феромона на нем – как
, а интенсивность феромона на нем – как 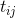 . Тогда вероятность перехода муравья из
. Тогда вероятность перехода муравья из 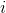 в
в 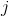 будет равна:
будет равна: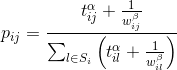
где
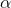 и
и 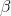 – это регулируемые параметры, определяющие важность составляющих (веса ребра и уровня феромонов) при выборе пути. Очевидно, что при
– это регулируемые параметры, определяющие важность составляющих (веса ребра и уровня феромонов) при выборе пути. Очевидно, что при  алгоритм превращается в классический жадный алгоритм, а при
алгоритм превращается в классический жадный алгоритм, а при  он быстро сойдется к некоторому субоптимальному решению. Выбор правильного соотношения параметров является предметом исследований, и в общем случае производится на основании опыта.
он быстро сойдется к некоторому субоптимальному решению. Выбор правильного соотношения параметров является предметом исследований, и в общем случае производится на основании опыта.После того, как муравей успешно проходит маршрут, он оставляет на всех пройденных ребрах след, обратно пропорциональный длине пройденного пути:
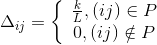 ,
,где
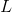 – длина пути, а
– длина пути, а 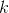 – регулируемый параметр. Кроме этого, следы феромона испаряются, то есть интенсивность феромона на всех ребрах уменьшается на каждой итерации алгоритма. Таким образом, в конце каждой итерации необходимо обновить значения интенсивностей:
– регулируемый параметр. Кроме этого, следы феромона испаряются, то есть интенсивность феромона на всех ребрах уменьшается на каждой итерации алгоритма. Таким образом, в конце каждой итерации необходимо обновить значения интенсивностей:\cdot t_{ij} +\Delta t_{ij})
Обзор модификаций классического алгоритма
Результаты первых экспериментов с применением муравьиного алгоритма для решения задачи коммивояжера были многообещающими, однако далеко не лучшими по сравнению с уже существовавшими методами. Однако простота классического муравьиного алгоритма (названного «муравьиной системой») оставляла возможности для доработок – и именно алгоритмические усовершенствования стали предметом дальнейших исследований Марко Дориго и других специалистов в области комбинаторной оптимизации. В основном, эти усовершенствования связаны с большим использованием истории поиска и более тщательным исследованием областей вокруг уже найденных удачных решений. Ниже рассмотрены наиболее примечательные из модификаций.
Elitist Ant System
Одним из таких усовершенствований является введение в алгоритм так называемых «элитных муравьев». Опыт показывает, что проходя ребра, входящие в короткие пути, муравьи с большей вероятностью будут находить еще более короткие пути. Таким образом, эффективной стратегией является искусственное увеличение уровня феромонов на самых удачных маршрутах. Для этого на каждой итерации алгоритма каждый из элитных муравьев проходит путь, являющийся самым коротким из найденных на данный момент.
Эксперименты показывают, что, до определенного уровня, увеличение числа элитных муравьев является достаточно эффективным, позволяя значительно сократить число итераций алгоритма. Однако, если число элитных муравьев слишком велико, то алгоритм достаточно быстро находит субоптимальные решение и застревает в нем [3]. Как и другие изменяемые параметры, оптимальное число элитных муравьев следует определять опытным путем.
Ant-Q
Лука Гамбарделла (Luca M. Gambardella) и Марко Дориго опубликовали в 1995 году работу, в которой они представили муравьиный алгоритм, получивший свое название по аналогии с методом машинного обучения Q-learning [4]. В основе алгоритма лежит идея о том, что муравьиную систему можно интерпретировать как систему обучения с подкреплением. Ant-Q усиливает эту аналогию, заимствуя многие идеи из Q-обучения.
Алгоритм хранит Q-таблицу, сопоставляющую каждому из ребер величину, определяющую «полезность» перехода по этому ребру. Эта таблица изменяется в процессе работы алгоритма – то есть обучения системы. Значение полезности перехода по ребру вычисляется исходя из значений полезностей перехода по следующим ребрам в результате предварительного определения возможных следующих состояний. После каждой итерации полезности обновляются исходя из длин путей, в состав которых были включены соответствующие ребра.
Ant Colony System
В 1997 году те же исследователи опубликовали работу, посвященную еще одному разработанному ими муравьиному алгоритму [5]. Для повышения эффективности по сравнению с классическим алгоритмом, ими были введены три основных изменения.
Во-первых, уровень феромонов на ребрах обновляется не только в конце очередной итерации, но и при каждом переходе муравьев из узла в узел. Во-вторых, в конце итерации уровень феромонов повышается только на кратчайшем из найденных путей. В-третьих, алгоритм использует измененное правило перехода: либо, с определенной долей вероятности, муравей безусловно выбирает лучшее – в соответствие с длиной и уровнем феромонов – ребро, либо производит выбор так же, как и в классическом алгоритме.
Max-min Ant System
В том же году Томас Штютцле (Tomas Stützle) и Хольгер Хоос (Holger Hoos) предложили муравьиный алгоритм, в котором повышение концентрации феромонов происходит только на лучших путях из пройденных муравьями [6]. Такое большое внимание к локальным оптимумам компенсируется вводом ограничений на максимальную и минимальную концентрацию феромонов на ребрах, которые крайне эффективно защищают алгоритм от преждевременной сходимости к субоптимальным решениям.
На этапе инициализации, концентрация феромонов на всех ребрах устанавливается равной максимальной. После каждой итерации алгоритма только один муравей оставляет за собой след – либо наиболее успешный на данной итерации, либо, аналогично алгоритму с элитизмом, элитный. Этим достигается, с одной стороны, более тщательное исследование области поиска, с другой – его ускорение.
ASrank
Бернд Бульнхаймер (Bernd Bullnheimer), Рихард Хартл (Richard F. Hartl) и Кристине Штраусс (Christine Strauß) разработали модификацию классического муравьиного алгоритма, в котором в конце каждой итерации муравьи ранжируются в соответствие с длинами пройденных ими путей [7]. Количество феромонов, оставляемого муравьем на ребрах, таким образом, назначается пропорционально его позиции. Кроме того, для более тщательного исследования окрестностей уже найденных удачных решений, алгоритм использует элитных муравьев.
Заключение
Задача коммивояжера является, возможно, наиболее исследуемой задачей комбинаторной оптимизации. Неудивительно, что именно она была выбрана первой для решения с использованием подхода, заимствующего механизмы поведения муравьиной колонии. Позже этот подход нашел применение в решении многих других комбинаторных проблем, в числе которых задачи о назначениях, задача раскраски графа, задачи маршрутизации, задачи из областей data mining и распознавания образов и другие.
Эффективность муравьиных алгоритмов сравнима с эффективностью общих метаэвристических методами, а в ряде случаев – и с проблемно-ориентированными методами. Наилучшие результаты муравьиные алгоритмы показывают для задач с большими размерностями областей поиска. Муравьиные алгоритмы хорошо подходят для применения вместе с процедурами локального поиска, позволяя быстро находить начальные точки для них.
Наиболее перспективными направлениями дальнейших исследований в данном направлении следует считать анализ способа выбора настраиваемых параметров алгоритмов. В последние годы предлагаются различные способы адаптации параметров алгоритмов «на лету» [8]. Поскольку от выбора параметров сильно зависит поведение муравьиных алгоритмов, именно к этой проблеме обращено наибольшее внимание исследователей на данный момент.
Литература
[1] M. Dorigo, “Ottimizzazione, apprendimento automatico, ed algoritmi basati su metafora naturale (Optimization, Learning, and Natural Algorithms)”, диссертация на соискание ученой степени “Doctorate in Systems and Information Electronic Engineering”, Politecnico di Milano, 1992 г.
[2] A. Colorni, M. Dorigo, V. Maniezzo, “Distributed Optimization by Ant Colonies” // Proceedings of the First European Conference on Artificial Life, Paris, France, Elsevier Publishing, стр. 134-142, 1991 г.
[3] M. Dorigo, V. Maniezzo, A. Colorni, “The Ant System: Optimization by a colony of cooperating agents” // IEEE Transactions on Systems, Man, and Cybernetics-Part B, 26, 1, стр. 29-41, 1996 г.
[4] L. M. Gambardella, M. Dorigo, “Ant-Q: A Reinforcement Learning Approach to the Traveling Salesman Problem” // Twelfth International Conference on Machine Learning, Morgan Kaufmann, стр. 252-260, 1995 г.
[5] M. Dorigo, L. M. Gambardella, Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem // IEEE Transactions on Evolutionary Computation Vol. 1, 1, стр. 53-66, 1997 г.
[6] T. Stützle, H. Hoos, “MAX-MIN Ant System and local search for the traveling salesman problem” // IEEE International Conference on Evolutionary Computation, стр. 309-314, 1997 г.
[7] Bernd Bullnheimer, Richard F. Hartl, Christine Strauß, “A new rank based version of the Ant System. A computational study” // Adaptive Information Systems and Modelling in Economics and Management Science, 1, 1997 г.
[8] T. Stützle, M. López-Ibáñez, P. Pellegrini, M. Maur, M. de Oca, M. Birattari, Michael Maur, M. Dorigo, “Parameter Adaptation in Ant Colony Optimization” // Technical Report, IRIDIA, Université Libre de Bruxelles, 2010 г.