Предисловие
— Кибердворник дядя Федя силой ровно в три медведя, — сообщил Поль, извлекая из недр кибердворника блок регулировки. — Я тут уже знаю одного Федю. Приятный такой, веснушчатый. Очень, очень асептический молодой человек. Это не твой родственник?
Аркадий и Борис Стругацкие (Полдень. ХХII век).
Статья посвящена вопросу применимости генетических алгоритмов к проблеме идентификации динамической системы.
Обновлено: опубликовано продолжение ТАУ-Дарвинизм: реализация на Ruby
Введение
Идентификация структуры математической модели, как часть анализа физических систем, означает отыскание алгебраического выражения (уравнения), описывающего физическую модель объекта. Многие методы идентификации систем относятся к параметрическим, т.е. определяется структура модели идентифицируемого объекта и по заданным формулам вычисляются значения параметров этой модели. В данной статье изложен метод подбора оптимальной математической модели объекта с использованием генетического программирования.
Преимуществом ГА в данном вопросе является то, что данные алгоритмы не ограничивают перечень систем, которые с их помощью можно идентифицировать и могут быть применены к любому набору данных, представляющих систему «вход-выход». При использовании ГА нет необходимости заранее определять структуру идентифицируемого объекта. Оптимальная структура модели будет найдена в процессе эволюционирования случайно сгенерированой популяции особей (моделей).
Терминология
- популяция — конечное множество особей;
- особь — организм, структура данных, представленная одной или более хромосом, каждая из которых есть точка в многомерном пространстве параметров решаемой задачи;
- хромосома — упорядоченный набор генов;
- ген — характеризуется позицией в хромосоме и содержит значение некоторого свойства (параметра);
- генотип — карта генов по совокупности хромосом;
- фенотип — набор возможных сочетаний генов в данном генотипе, т.е. облако точек в пространстве параметров задачи;
- аллели — набор возможных значений для каждого из генов, т.е. совокупность значений некоторого конкретного свойства;
- локус — позиция гена в хромосоме.
Объект идентификации
В качестве исходной математической модели идентифицируемего объекта будет рассматриваться неоднородное дифференциальное уравнение. Для простоты в качестве примера будет использовано дифференциальное уравнение второй степени:
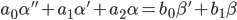 |
(1) |
В формуле (1) " ' " (апостроф) означает производную по времени — оператор d/dt; α — выходная координата (например, отклонение чувствительного элемента от положения равновесия); β — входное воздействие, управление (например, сила действующая на ЧЭ и приводящая к его отклонению).
В операторной форме записи (s = d/dt) это уравнение будет иметь вид:
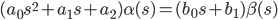 |
(2) |
По выражению (2) составляется передаточная функция — отношение выхода ко входу:
 |
(3) |
В (3) знаменатель является «характеристическим уравнением» системы. Оно определяет главные характеристики динамики (к примеру, устойчивость). Корни этого уравнения называются полюсами динамической системы. Корни числителя называются нулями динамической системы.
Передаточную функцию (3) можно переписать в виде дроби, числитель и знаменатель которой представляют собой произведения двух- и трехчленов:
 |
(4) |
В данном случае и числитель и знаменатель содержат по одному многочлену, но в общем случае для уравнений порядка 4 и более их будет несколько. При этом каждому из них соответствует точка на комплексной плоскости. Двучлену соответствует точка на вещественной оси, а трехчлену — точка, не лежащая на вещественной оси. Последнее утверждение верно только в случае, когда трехчлен имеет лишь два комплексно сопряженных корня. Иначе этот трехчлен можно будет представить в виде произведения двух двучленов.
В выражении (4) коэффициенты «T» — это постоянные времени, а коэффициент η — декремент затухатния колебаний (он же показатель колебательности или коэффициент дэмпфирования).
Генетическое кодирование
Для записи математической модели идентифицируемого объекта в форме (2) удобно использовать схему кодирования генов действительными числами. При этом количество аллелей каждого гена будет определяться разрядностью (количеством бит бинарного представления) действительных чисел в программной реализации алгоритмов.
Пусть математическую модель вида (2) кодируют две хромосомы — одна для входа (правая часть) и другая для выхода (левая часть). Гены в хромосомах соответствуют одному из слагаемых в уравнениях (2). Значение гена равно значению коэффициента при переменных в уравнениях. При этом количество генов в хромосомах может быть любым. При использовании такого подхода можно закодировать систему с входом и выходом любых порядков. В итоге это позволит закодировать динамическую систему с любой топологией и любым количеством обратных связей. Нужно лишь соблюдать правило физической реализуемости — порядок входа меньше или равен порядку выхода.
Недостатком такого подхода является то, что усложняется контроль характеристик динамики. Если сравнить (3) и (4), то легко заметить, что каждый из коэффициентов в (3) является комбинацией нескольких коэффициентов в (4). Поэтому с точки зрения синтеза оптимального регулятора может оказаться более выгодным использование записи модели в виде (4) даже в контексте ГА. В таком случае гены будут содержать значение полюса или нуля ПФ, причем значение это будет комплексным. При таком подходе к идентификации с использованием генетического программирования ожидается увеличение устойчивости особей в популяции и скорости сходимости алгоритма к оптимальному результату.
Независимо от выбора формы записи ПФ при использовании кодирования действительными (или комплексными) числами хромосома будет представлять собой массив чисел. Можно ввести и двоичное кодирование, задав квантование по уровню и приведя вещественные числа к целым в двоичном представлении («код Грэя» [2]). Однако часто в передаточных функциях соседствующие коэффициенты отличаются друг от друга на несколько порядков, поэтому могут возникнуть проблемы с точностью. Другим способом двоичного кодирования является логарифмическое (также см. в [2]), в котором первые два бита кодируют знаки числа и показателя степенной функции, а остальные — значение самого показателя степени. Использование двоичного кодирования с одной стороны усложнит алгоритм при использовании комплексных чисел, но с другой позволит использовать классические генетические операторы, требующие двоичного представления данных.
Функция приспособленности
Одним из главных понятий в ГА является понятие «функции приспособленности» или «фитнесс-функции». Она показывает насколько хорошо решение, представленное данной особью, удовлетворяет условиям поставленной задачи. В контексте задачи синтеза оптимального регулятора в качестве основного критерия оценки «приспособленности» особи можно использовать качество регулирования, т.е. хорошее сочетание сглаженности переходного процесса и его длительности. В задаче же идентификации более важна степень приближения реакции модели на входное воздействие к реакции реального (идентифицируемого) объекта на тоже воздействие. Оценивать степень приближенности можно по среднеквадратическому критерию, вычисляя среднеквадратическое отклонение реакции модели от записанного выходного сигнала идентифицтруемого объекта. В таком случае фитнесс-функция будет иметь вид формулы вычисления дисперсии:
 |
(5) |
В выражении (5) n — это число отсчетов в записанном выходном сигнале идентифицируемого объекта; xср — среднеарифметическое значение отклонения реакции данной особи от выходного сигнала идентифицируемого объекта.
Процедура вычисления «приспособленности» особи сводится к следующему. Сначала необходимо декодировать хромосому, т.е. по зашифрованным в ней значениям создать сначала непрерывную передаточную функцию (ПФ с непрерывным временем), а затем по этой ПФ составить дискретную модель, удобную для проведения численного моделирования. Мне удобнее всего пользоваться дискретной моделью в пространстве состояний [5].
На вход составленной дискретной модели подается воздействие, идентичное поданному на вход идентифицируемого объекта. Делается запись реакции особи на это воздействие. При этом модель особи составляется с периодом квантования по времени, равным периоду квантования выходного сигнала объекта. Далее нужно воспользоваться формулой (5), предварительно вычтя почленно из полученного массива элементы массива с записью выходного сигнала объекта, после чего можно разделить единицу на полученную дисперсию, если более приспособленными считаются особи с более высокими значениями фитнесс-функции.
Дополнительно можно ввести в фитнесс-функцию особое шкалирование (например, степенное) для того, чтобы самые плохо приспособленные особи отсеивались медленнее. Это необходимо сделать для поддержания генного разнообразия на должном уровне. Также необходимо добавить проверку особи на жизнеспособность. В качестве критериев такой оценки могут быть использованы следующие:
- порядок входа и выхода — нам не нужны модели со слишком большим порядком, а также модели, у которых порядок входа больше порядка выхода;
- длительность переходного процесса — приблизительно оценить время ПП можно не проводя моделирование (численный эксперимент) с участием данной модели; слишком длительный ПП нас также не устраивает;
- перерегулирование — отношение разности максимума реакции и установившегося значения к установившемуся значению;
- колебательность — нам не нужна модель с медленно затухающими автоколебаниями;
- устойчивость — легко определяется с помощью критерия Гурвица [4].
Скрещивание и мутация
В публикации [2, стр. 134] описан алгоритм одноточечного скрещивания. Он заключается в выборе локуса, в котором произойдет «слипание» хромосом и обмене полученными таким образом ветвями между хромосомами. В результате получатся две хромосомы, каждая из которых содержит в себе гены от обоих родителей. Можно создать по одной особи для каждой из хромосом или только одну особь для одной из хромосом.
В той же публикации описывается многоточечный метод скрещивания. Суть остается той же — создаются точки слипания и производится рекомбинация генных цепочек. Разница лишь в количестве возможных комбинаций генов и, соответственно в количестве получаемых комбинированных хромосом. Опять же можно создавать несколько особей (необязательно для каждой из хромосом), а можно лишь одну.
Сам алгоритм обмена генными цепочками можно модифицировать. Если вместо простой замены значений использовать вычисление некоторого взвешенного среднего, то будет создано подобие механизма конкуренции генов (доминантные гены и рецессивные). С той лишь разницей, что доминантность генов будет определяться приспособленностью особи.
Оператор мутации можно реализовать простым вычислением случайного значения для случайно выбранного гена, можно вычислять случайную прибавку к текущему значению гена, а можно применить инвертирование бита. Первый способ нежелателен, т.к. значения коэффициентов в передаточных функциях могут варьироваться в широком диапазоне, а смена значения одного коэффициента с очень малого на большое приведет к резкому изменению значения функции приспособленности и потере устойчивости модели. Та же опасность имеется и у бинарной мутации — смена бита, отвечающего за знак числа, может привести к потери устойчивости. Поэтому более оптимальным в данном случае является алгоритм вычисления случайной прибавки, приведенной к текущему значению гена. Данный подход означает, что диапазон, в котором выбирается случайное число, пропорционально текущему значению гена. Коэффициент пропорциональности можно выбрать равным нескольким единицам.
Эволюция популяции
На странице 211 в [2] представлен псевдокод эволюционирования популяции:

На каждом шаге итераций над особями популяции производятся стандартные процедуры генетического программирования: вычисление фитнесс-функций, селекция, скрещивание, мутация. Для эволюции популяции в целом ключевую роль играет процедура селекции. От нее зависит с какой скоростью и будет ли вообще популяция двигаться к глобальному оптимуму или застрянет в локальном экстремуме. Существует несколько подходов:
- колесо рулетки — каждая особь представлена на колесе сектором, величина которого пропорциональна значению фитнесс-функции особи;
- турнирный метод — популяция разбивается на подгруппы, внутри которых производится отбор по значению фитнесс-функции;
- ранговый метод — по значению фитнесс-функции особи назначается ранг, при этом чем больше ранг особи, тем меньше ее копий войдет в популяцию на следующем шаге итераций;
- комбинированные методы.
Следует заметить, что желательно ввести механизм защиты особей с наивысшими значениями фитнесс-функции от случайного выбывания. В классическом генетическом алгоритме существует небольшая вероятность того, что самая приспособленная особь не войдет в новую популяцию. Поэтому особь с максимальным значением фитнесс-функции должна быть защищена от случайного выбывания. Такая стратегия называется «элитарной».
Существует также стратегия перехода части особей в новую популяцию без применения к ним генетических операций, т.е. родители не погибают сразу после рождения потомства. В дополнение к этой стратегии можно ввести в фитнесс-функцию возрастной штраф, т.е. уменьшение ее значения пропорционально возрасту особи.
Еще одной важной модификацией ГА является «нишевание». В соответствии с ней в фитнесс-функцию добавляется коэффициент, обратно пропорциональный количеству и близости соседей в многомерном пространстве оптимизируемых параметров. В результате модифицированная фитнесс-функция будет иметь вид:
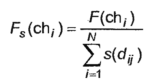 |
(6) |
Если особь находится в своей нише в одиночестве, т.е. нет похожих на нее соседей, то значение фитнесс-функции не будет изменено. В противном случае ее значение будет уменьшено пропорционально близости и количеству соседей по нише. При этом степень близости можно оценивать различными способами.
Введение нишевания позволяет найти несколько экстремумов, т.е. сразу несколько оптимальных моделей, близких по характеристикам динамики к идентифицируемому объекту, но при этом отличающиеся друг от друга.
Заключение
В заключение хотелось бы сказать, что в настоящее время генетические алгоритмы вместе с различными модификациями, часть из которых рассмотрены в данной статье, и эволюционные стратегии объединены под одним общим названием «эволюционные алгоритмы». Изначально генетические алгоритмы и эволюционные стратегии развивались независимо друг от друга. Но позже специалисты стали комбинировать методики из этих двух областей. В настоящее время разница между ними не столь заметна. Многое из изложенного в статье правильнее было бы отнести к эволюционным стратегиям, но для простоты восприятия было решено оставить все как есть.
Спасибо за внимание! Ваши комментарии…
Update 1: по просьбам читателей расширяю список литературы.
Список литературы
1. Stephan WINKLER, Michael AFFENZELLER, Stefan WAGNER. NEW METHODS FOR THE IDENTIFICATION OF NONLINEAR MODEL STRUCTURES BASED UPON GENETIC PROGRAMMING TECHNIQUES // Institute of Systems Theory and Simulation, Johannes Kepler University Linz, Austria {winkler,ma,sw}@cast.uni-linz.ac.at
2. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. — М.: Горячая линия — Телеком, 2006. — 452 с.: ил.
3. Ход «Voronoi»
4. Критерий устойчивости Рауса-Гурвица
5. Пространство состояний (теория управления)
6. Концепции практического использования генетических алгоритмов
7. «Hello world!» с помощью генетических алгоритмов
8. Генетический алгоритм
9. Эволюционные алгоритмы