Аннотация
В данной статье рассказывается об уникальном фильтре, статья о котором появилась в 1990 году: Маслов А.М., Сергеев В.В. Идентификация линейной искажающей системы с использованием ранговой обработки сигналов // Компьютерная оптика. — М., 1990. — Вып.6. — С.97-102. Данный алгоритм получил название «Алгоритм ранговой обработки» и по факту является обобщением медианного фильтра.
Применение данного фильтра оправдано в двух случая — для подавления шума и для уменьшения смаза.
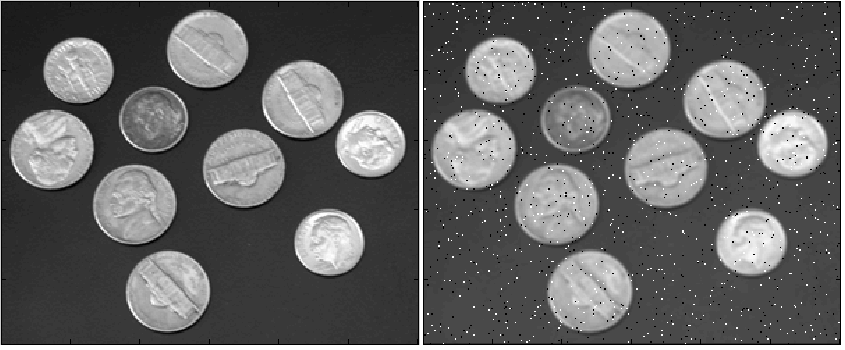
Рисунок 1 — исходное изображение, 2 — смазанное и зашумленное солью.
Алгоритм ранговой обработки сигнала — экстремальный фильтр
Алгоритм заключается в обработке изображения локальным окном с записью результата обработки в новое изображение:
- Пусть мы находимся в точке изображения с координатами (I,J) - текущий отсчет
- Вокруг текущего отсчета рассматривается локальная окрестность размера NxN
- По значениям точек в лоальной окрестности строится вариационный ряд, который обозначим p. Размер данного ряда N*N.
- В результирующем изображении текущий отсчет принимает значение по следующему правилу:
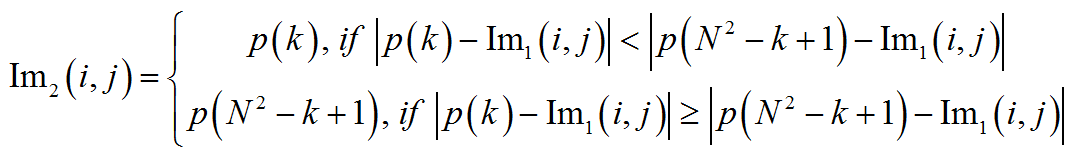
где k — параметр алгоритма, N — нечетное число, Im1 — исходное изображение, Im2 — результирующее изображение.
Если k = (N^2+1)/2 — то есть центр вариационного ряда — данный фильтр становится известным медианным фильтром. В дальнейшем этот параметр будем называть отступом.
Свойства экстремального фильтра
Свойства данного фильтр очень полезны на практике, так как фильтр позволяет компенсировать не только шум но устранять (частично) последствия смаза изображения. Предельным случаем этого фильтра при k = (N^2+1)/2 мы имеем медианный фильтр, который только устраняет шум, но не трогает границы, и если изображение смазанное, то смаз так и останется.
При k < (N^2+1)/2 шум фильтруется несколько хуже, зато повышается резкость изображения, а при k = 0 шум и вовсе не фильтруется, но смаз устранятся самым сильным образом.
Дабы не утруждать читателей элементарной реализацией данного алгоритма, я приведу здесь код на Matlab.
Тестирующий скрипт будет читать изображение, смазывать его, и добавлять шум. Затем изображение восстанавливается данным экстремальным фильтров.
- I1 = imread('coins.png');
- h = ones(3,3) / 9;
- I2 = imfilter(I1,h) ;
- I3 = imnoise(I2,'salt & pepper',0.02);
- I4 = im2_rang_filter (I3, 1, 2);
-
- figure; imagesc(I1);
- colormap gray;
- figure; imagesc(I3);
- colormap gray;
- figure; imagesc(I4)
- colormap gray;
* This source code was highlighted with Source Code Highlighter.
Код функции фильтра im2_rang_filter:
- function outImage= im2_rang_filter (aImage, aHalfWindowSize, aOtsup)
- [ver,hor] = size(aImage);
- wsize = (aHalfWindowSize*2+1)^2;
- result = zeros(ver,hor);
- for i = aHalfWindowSize+1 : (ver - aHalfWindowSize)
- for j = aHalfWindowSize+1 : (hor - aHalfWindowSize)
-
- wind = aImage((i-aHalfWindowSize) : (i + aHalfWindowSize), (j-aHalfWindowSize) : (j + aHalfWindowSize));
- vec = reshape(wind,1,wsize);
- vec = sort(vec);
-
- if (abs(vec(aOtsup+1) - aImage(i,j)) < abs(vec(wsize - aOtsup) - aImage(i,j)) )
- result(i,j) = vec(aOtsup+1);
- else result(i,j) = vec(wsize - aOtsup);
- end;
-
- end;
- end;
- outImage = result;
* This source code was highlighted with Source Code Highlighter.
Экперименты
Ниже показаны результаты фильтрации окном 3 на 3 при варьировании параметра k = 1,2,5. Первый рисунок — исходное изображение, второй рисунок — искаженное, далее друг за другом идут отфильтрованные при k=1, 2, 5:
Исходное:

Искаженное:
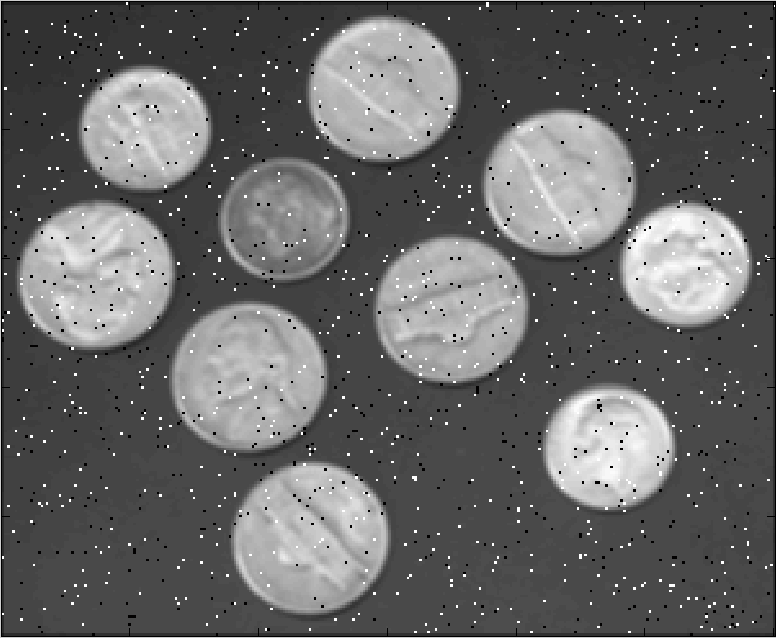
Восстановленное при k=1:

Восстановленное при k=2:

Восстановленное при k=5:

Мне этот фильтр очень нравится и я активно использую его на практике. Интересно мнение читателей об это фильтре.