Введение
Алгоритмы нечеткого поиска (также известного как поиск по сходству или fuzzy string search) являются основой систем проверки орфографии и полноценных поисковых систем вроде Google или Yandex. Например, такие алгоритмы используются для функций наподобие «Возможно вы имели в виду …» в тех же поисковых системах.
В этой обзорной статье я рассмотрю следующие понятия, методы и алгоритмы:
- Расстояние Левенштейна
- Расстояние Дамерау-Левенштейна
- Алгоритм Bitap с модификациями от Wu и Manber
- Алгоритм расширения выборки
- Метод N-грамм
- Хеширование по сигнатуре
- BK-деревья
Итак...
Нечеткий поиск является крайне полезной функцией любой поисковой системы. Вместе с тем, его эффективная реализация намного сложнее, чем реализация простого поиска по точному совпадению.
Задачу нечеткого поиска можно сформулировать так:
«По заданному слову найти в тексте или словаре размера n все слова, совпадающие с этим словом (или начинающиеся с этого слова) с учетом k возможных различий».
Например, при запросе «Машина» с учетом двух возможных ошибок, найти слова «Машинка», «Махина», «Малина», «Калина» и так далее.
Алгоритмы нечеткого поиска характеризуются метрикой — функцией расстояния между двумя словами, позволяющей оценить степень их сходства в данном контексте. Строгое математическое определение метрики включает в себя необходимость соответствия условию неравенства треугольника (X — множество слов, p — метрика):
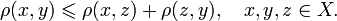
Между тем, в большинстве случаев под метрикой подразумевается более общее понятие, не требующее выполнения такого условия, это понятие можно также назвать расстоянием.
В числе наиболее известных метрик — расстояния Хемминга, Левенштейна и Дамерау-Левенштейна. При этом расстояние Хемминга является метрикой только на множестве слов одинаковой длины, что сильно ограничивает область его применения.
Впрочем, на практике расстояние Хемминга оказывается практически бесполезным, уступая более естественным с точки зрения человека метрикам, о которых и пойдет речь ниже.
Расстояние Левенштейна
Наиболее часто применяемой метрикой является расстояние Левенштейна, или расстояние редактирования, алгоритмы вычисления которого можно найти на каждом шагу.
Тем не менее, стоит сделать несколько замечаний относительно наиболее популярного алгоритма расчета — метода Вагнера-Фишера.
Исходный вариант этого алгоритма имеет временную сложность O(mn) и потребляет O(mn) памяти, где m и n — длины сравниваемых строк. Весь процесс можно представить следующей матрицей:
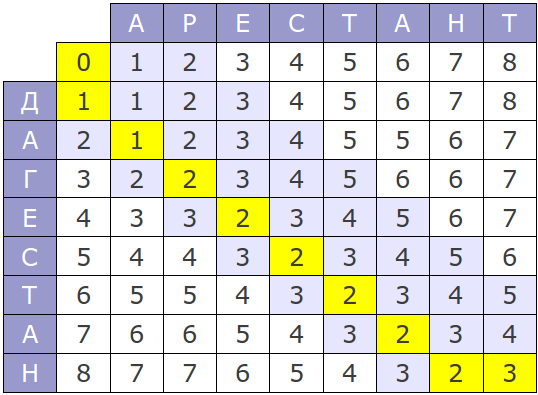
Если посмотреть на процесс работы алгоритма, несложно заметить, что на каждом шаге используются только две последние строки матрицы, следовательно, потребление памяти можно уменьшить до O(min(m, n)).
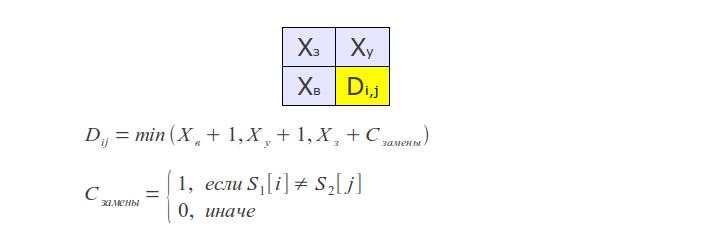
Но это еще не всё — можно дальше оптимизировать алгоритм, если стоит задача нахождения не более k различий. В этом случае нужно вычислять в матрице лишь диагональную полосу шириной 2k+1 (отсечение Укконена), что сводит временную сложность к O(k min(m, n)).
Префиксное расстояние
Также бывает необходимо вычислять расстояние между префиксом-образцом и строкой — т. е. найти расстояние между заданным префиксом и ближайшим префиксом строки. В этом случае необходимо взять наименьшее из расстояний от префикса-образца до всех префиксов строки. Очевидно, что префиксное расстояние не может считаться метрикой в строгом математическом смысле, что ограничивает его применение.
Зачастую при нечетком поиске важно не столько само значение расстояния, сколько факт того, превышает оно или нет определенную величину.
Расстояние Дамерау-Левенштейна
Эта вариация вносит в определение расстояния Левенштейна еще одно правило — транспозиция (перестановка) двух соседних букв также учитывается как одна операция, наряду со вставками, удалениями и заменами.
Еще пару лет назад Фредерик Дамерау мог бы гарантировать, что большинство ошибок при наборе текста — как раз и есть транспозиции. Поэтому именно данная метрика дает наилучшие результаты на практике.

Чтобы вычислять такое расстояние, достаточно немного модифицировать алгоритм нахождения обычного расстояния Левенштейна следующим образом: хранить не две, а три последних строки матрицы, а также добавить соответствующее дополнительное условие — в случае обнаружения транспозиции при расчете расстояния также учитывать и её стоимость.
Кроме рассмотренных выше, существует еще множество других, иногда применяющихся на практике расстояний, таких как метрика Джаро-Винклера, многие из которых доступны в библиотеках SimMetrics и SecondString.
Алгоритмы нечеткого поиска без индексации (Онлайн)
Эти алгоритмы предназначены для поиска по заранее неизвестному тексту, и могут быть использованы, например, в текстовых редакторах, программах для просмотра документов или в веб-браузерах для поиска по странице. Они не требуют предварительной обработки текста и могут работать с непрерывным потоком данных.
Линейный поиск
Простое последовательное применение заданной метрики (например, метрики Левенштейна) к словам из входного текста. При использовании метрики с ограничением, этот метод позволяет добиться оптимальной скорости работы. Но, при этом, чем больше k, тем сильнее возрастает время работы. Асимптотическая оценка времени — O(kn).
Bitap (также известный как Shift-Or или Baeza-Yates-Gonnet, и его модификация от Wu-Manber)
Алгоритм Bitap и различные его модификации наиболее часто используются для нечеткого поиска без индексации. Его вариация используется, например, в unix-утилите agrep, выполняющей функции аналогично стандартному grep, но с поддержкой ошибок в поисковом запросе и даже предоставляя ограниченные возможности для применения регулярных выражений.
Впервые идею этого алгоритма предложили граждане Ricardo Baeza-Yates и Gaston Gonnet, опубликовав соответствующую статью в 1992 году.
Оригинальная версия алгоритма имеет дело только с заменами символов, и, фактически, вычисляет расстояние Хемминга. Но немного позже Sun Wu и Udi Manber предложили модификацию этого алгоритма для вычисления расстояния Левенштейна, т.е. привнесли поддержку вставок и удалений, и разработали на его основе первую версию утилиты agrep.
Операция Bitshift
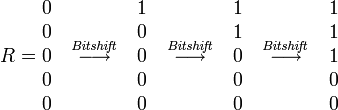
Вставки
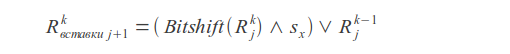
Удаления
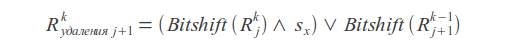
Замены

Результирующее значение
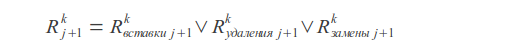
Где k — количество ошибок, j — индекс символа, sx — маска символа (в маске единичные биты располагаются на позициях, соответствующих позициям данного символа в запросе).
Совпадение или несовпадение запросу определяется самым последним битом результирующего вектора R.
Высокая скорость работы этого алгоритма обеспечивается за счет битового параллелизма вычислений — за одну операцию возможно провести вычисления над 32 и более битами одновременно.
При этом тривиальная реализация поддерживает поиск слов длиной не более 32. Это ограничение обуславливается шириной стандартного типа int (на 32-битных архитектурах). Можно использовать и типы больших размерностей, но это может в некоторой степени замедлить работу алгоритма.
Не смотря на то, что асимптотическое время работы этого алгоритма O(kn) совпадает с таковым у линейного метода, он значительно быстрее при длинных запросах и количестве ошибок k более 2.
Тестирование
Тестирование осуществлялось на тексте 3.2 млн слов, средняя длина слова — 10.
Точный поиск
Время поиска: 3562 мсПоиск с использованием метрики Левенштейна
Время поиска при k=2: 5728 мсВремя поиска при k=5: 8385 мс
Поиск с использованием алгоритма Bitap с модификациями Wu-Manber
Время поиска при k=2: 5499 мсВремя поиска при k=5: 5928 мс
Очевидно, что простой перебор с использованием метрики, в отличие от алгоритма Bitap, сильно зависит от количества ошибок k.
Тем не менее, если речь заходит о поиске в неизменных текстах большого объема, то время поиска можно значительно сократить, произведя предварительную обработку такого текста, также называемую индексацией.
Алгоритмы нечеткого поиска с индексацией (Оффлайн)
Особенностью всех алгоритмов нечеткого поиска с индексацией является то, что индекс строится по словарю, составленному по исходному тексту или списку записей в какой-либо базе данных.
Эти алгоритмы используют различные подходы к решению проблемы — одни из них используют сведение к точному поиску, другие используют свойства метрики для построения различных пространственных структур и так далее.
Прежде всего, на первом шаге по исходному тексту строится словарь, содержащий слова и их позиции в тексте. Также, можно подсчитывать частоты слов и словосочетаний для улучшения качества результатов поиска.
Предполагается, что индекс, как и словарь, целиком загружен в память.
Тактико-технические характеристики словаря:
- Исходный текст — 8.2 гигабайта материалов библиотеки Мошкова (lib.ru), 680 млн слов;
- Размер словаря — 65 мегабайт;
- Количество слов — 3.2 млн;
- Средняя длина слова — 9.5 символов;
- Средняя квадратичная длина слова (может быть полезна при оценке некоторых алгоритмов) — 10.0 символов;
- Алфавит — заглавные буквы А-Я, без Ё (для упрощения некоторых операций). Слова, содержащие символы не из алфавита, не включены в словарь.

Алгоритм расширения выборки
Этот алгоритм часто применяется в системах проверки орфографии (т.е. в spell-checker'ах), там, где размер словаря невелик, либо же где скорость работы не является основным критерием.
Он основан на сведении задачи о нечетком поиске к задаче о точном поиске.
Из исходного запроса строится множество «ошибочных» слов, для каждого из которых затем производится точный поиск в словаре.
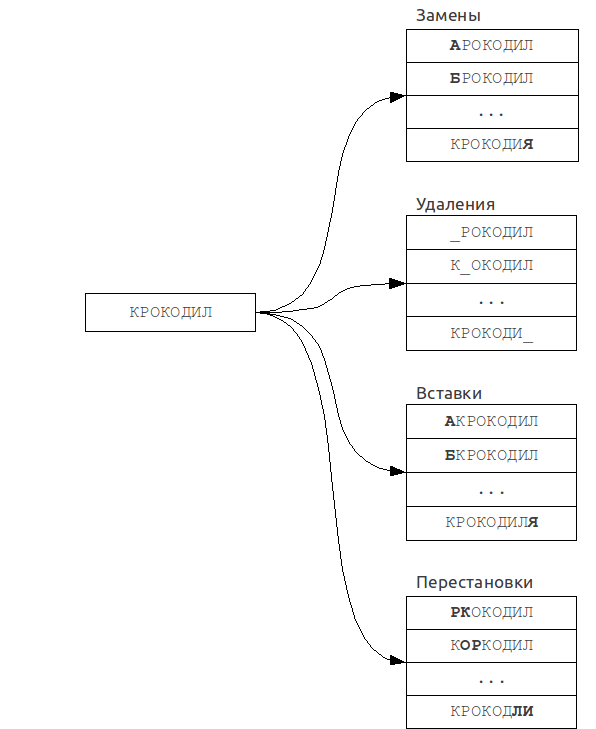
Время его работы сильно зависит от числа k ошибок и от размера алфавита A, и в случае использования бинарного поиска по словарю составляет:
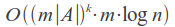
Например, при k = 1 и слова длины 7 (например, «Крокодил») в русском алфавите множество ошибочных слов будет размером около 450, то есть будет необходимо сделать 450 запросов к словарю, что вполне приемлемо.
Но уже при k = 2 размер такого множества будет составлять более 115 тысяч вариантов, что соответствует полному перебору небольшого словаря, либо же 1 / 27 в нашем случае, и, следовательно, время работы будет достаточно велико. При этом не нужно забывать еще и о том, что для каждого из таких слов необходимо провести поиск на точное совпадение в словаре.
Особенности:
Алгоритм может быть легко модифицирован для генерации «ошибочных» вариантов по произвольным правилам, и, к тому же, не требует никакой предварительной обработки словаря, и, соответственно, дополнительной памяти.Возможные улучшения:
Можно генерировать не всё множество «ошибочных» слов, а только те из них, которые наиболее вероятно могут встретиться в реальной ситуации, например, слова с учетом распространенных орфографических ошибок или ошибок набора.Метод N-грамм
Этот метод был придуман довольно давно, и является наиболее широко используемым, так как его реализация крайне проста, и он обеспечивает достаточно хорошую производительность. Алгоритм основывается на принципе:
«Если слово А совпадает со словом Б с учетом нескольких ошибок, то с большой долей вероятности у них будет хотя бы одна общая подстрока длины N».
Эти подстроки длины N и называются N-граммами.
Во время индексации слово разбивается на такие N-граммы, а затем это слово попадает в списки для каждой из этих N-грамм. Во время поиска запрос также разбивается на N-граммы, и для каждой из них производится последовательный перебор списка слов, содержащих такую подстроку.
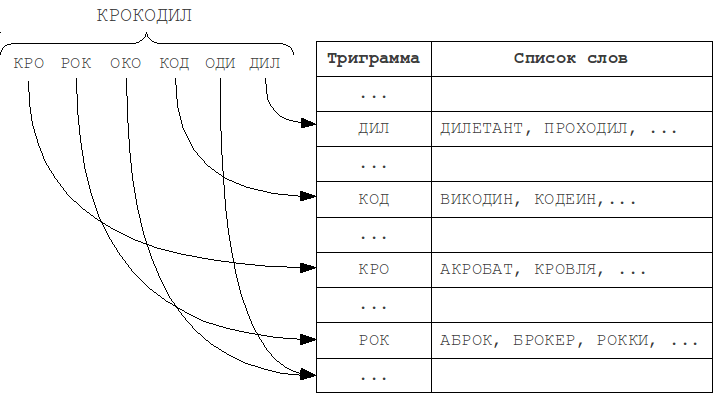
Наиболее часто используемыми на практике являются триграммы — подстроки длины 3. Выбор большего значения N ведет к ограничению на минимальную длину слова, при которой уже возможно обнаружение ошибок.
Особенности:
Алгоритм N-грамм находит не все возможные слова с ошибками. Если взять, например, слово ВОТКА, и разложить его на триграммы: ВОТКА → ВОТ ОТК ТКА — то можно заметить, что они все содержат ошибку Т. Таким образом, слово «ВОДКА» найдено не будет, так как оно не содержит ни одной из этих триграмм, и не попадет в соответствующие им списки. Таким образом, чем меньше длина слова и чем больше в нем ошибок, тем выше шанс того, что оно не попадет в соответствующие N-граммам запроса списки, и не будет присутствовать в результате.Между тем, метод N-грамм оставляет полный простор для использования собственных метрик с произвольными свойствами и сложностью, но за это приходится платить — при его использовании остается необходимость в последовательном переборе около 15% словаря, что достаточно много для словарей большого объема.
Возможные улучшения:
Можно разбивать хеш-таблицы N-грамм по длине слов и по позиции N-граммы в слове (модификация 1). Как длина искомого слова и запроса не могут отличаться более чем на k, так и позиции N-граммы в слове могут различаться не более чем на k. Таким образом, необходимо будет проверить лишь таблицу, соответствующую позиции этой N-граммы в слове, а также k таблиц слева и k таблиц справа, т.е. всего 2k+1 соседних таблиц.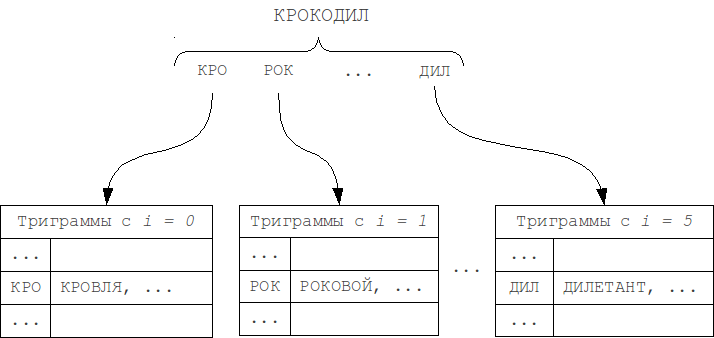
Можно еще немного уменьшить размер необходимого для просмотра множества, разбив таблицы по длине слова, и аналогичным образом просматривая только соседние 2k+1 таблицы (модификация 2).
Хеширование по сигнатуре
Этот алгоритм описан в статье Бойцова Л.М. «Хеширование по сигнатуре». Он базируется на достаточно очевидном представлении «структуры» слова в виде битовых разрядов, используемой в качестве хеша (сигнатуры) в хеш-таблице.
При индексации такие хеши вычисляются для каждого из слов, и в таблицу заносится соответствие списка словарных слов этому хешу. Затем, во время поиска, для запроса вычисляется хеш и перебираются все соседние хеши, отличающиеся от исходного не более чем в k битах. Для каждого из таких хешей производится перебор списка соответствующих ему слов.
Процесс вычисления хеша — каждому биту хеша сопоставляется группа символов из алфавита. Бит 1 на позиции i в хеше означает, что в исходном слове присутствует символ из i-ой группы алфавита. Порядок букв в слове абсолютно никакого значения не имеет.
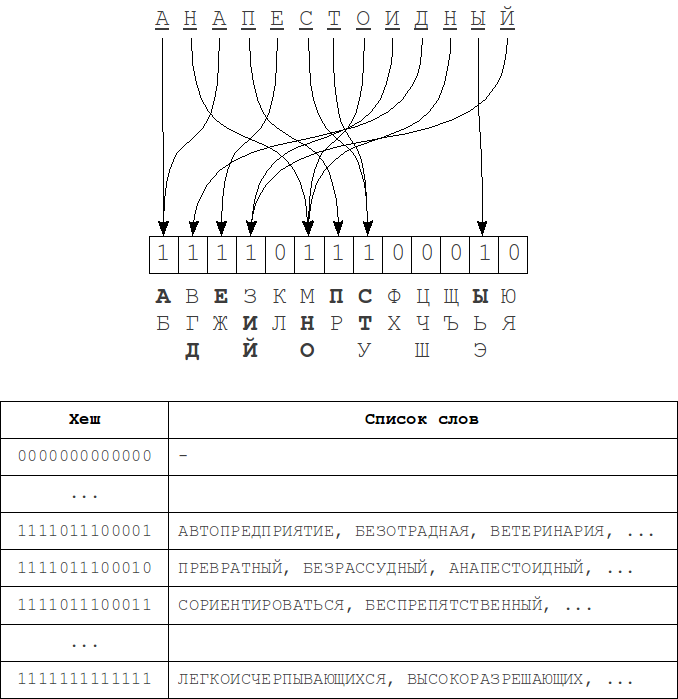
Удаление одного символа либо не изменит значения хеша (если в слове еще остались символы из той же группы алфавита), либо же соответствующий этой группе бит изменится в 0. При вставке, аналогичным образом либо один бит встанет в 1, либо никаких изменений не будет. При замене символов всё немного сложнее — хеш может либо вовсе остаться неизменным, либо же изменится в 1 или 2 позициях. При перестановках никаких изменений и вовсе не происходит, потому что порядок символов при построении хеша, как и было замечено ранее, не учитывается. Таким образом, для полного покрытия k ошибок нужно изменять не менее 2k бит в хеше.
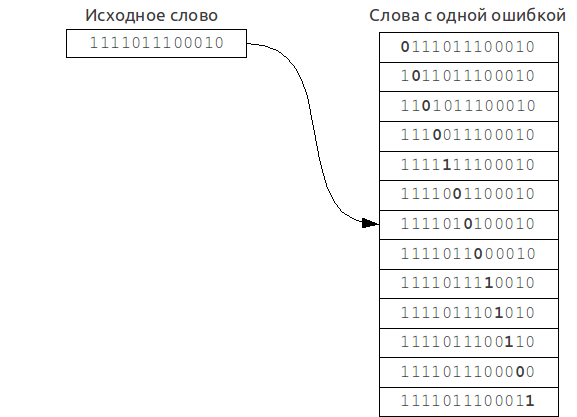
Время работы, в среднем, при k «неполных» (вставки, удаления и транспозиции, а также малая часть замен) ошибках:
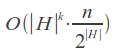
Особенности:
Из того, что при замене одного символа могут изменятся сразу два бита, алгоритм, реализующий, например, искажения не более 2 битов одновременно в действительности не будет выдавать полного объема результатов из-за отсутствия значительной (зависит от отношения размера хеша к алфавиту) части слов с двумя заменами (и чем больше размер хеша, тем чаще замена символа будет приводить к искажению сразу двух бит, и тем менее полным будет результат). К тому же, этот алгоритм не позволяет проводить префиксный поиск.BK-деревья
Деревья Burkhard-Keller являются метрическими деревьями, алгоритмы построения таких деревьев основаны на свойстве метрики отвечать неравенству треугольника:
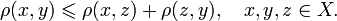
Это свойство позволяет метрикам образовывать метрические пространства произвольной размерности. Такие метрические пространства не обязательно являются евклидовыми, так, например, метрики Левенштейна и Дамерау-Левенштейна образуют неевклидовы пространства. На основании этих свойств можно построить структуру данных, осуществляющую поиск в таком метрическом пространстве, которой и являются деревья Баркхарда-Келлера.
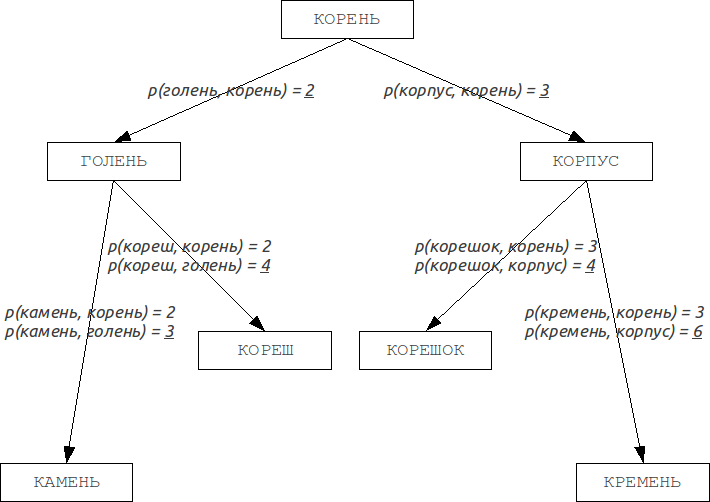
Улучшения:
Можно использовать возможность некоторых метрик вычислять расстояние с ограничением, устанавливая верхний предел, равный сумме максимального расстояния к потомкам вершины и результирующего расстояния, что позволит немного ускорить процесс: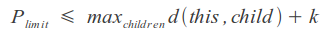
Тестирование
Тестирование осуществлялось на ноутбуке с Intel Core Duo T2500 (2GHz/667MHz FSB/2MB), 2Gb ОЗУ, ОС — Ubuntu 10.10 Desktop i686, JRE — OpenJDK 6 Update 20.
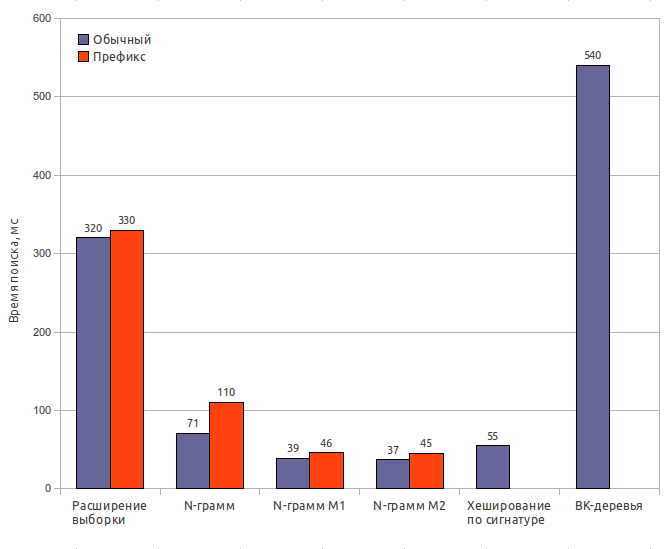
Тестирование осуществлялось с использованием расстояния Дамерау-Левенштейна и количеством ошибок k = 2. Размер индекса указан вместе со словарем (65 Мб).
Расширение выборки
Размер индекса: 65 МбВремя поиска: 320 мс / 330 мс
Полнота результатов: 100%
N-грамм (оригинальный)
Размер индекса: 170 МбВремя создания индекса: 32 с
Время поиска: 71 мс / 110 мс
Полнота результатов: 65%
N-грамм (модификация 1)
Размер индекса: 170 МбВремя создания индекса: 32 с
Время поиска: 39 мс / 46 мс
Полнота результатов: 63%
N-грамм (модификация 2)
Размер индекса: 170 МбВремя создания индекса: 32 с
Время поиска: 37 мс / 45 мс
Полнота результатов: 62%
Хеширование по сигнатуре
Размер индекса: 85 МбВремя создания индекса: 0.6 с
Время поиска: 55 мс
Полнота результатов: 56.5%
BK-деревья
Размер индекса: 150 МбВремя создания индекса: 120 с
Время поиска: 540 мс
Полнота результатов: 63%
Итого
Большинство алгоритмов нечеткого поиска с индексацией не являются истинно сублинейными (т.е. имеющими асимптотическое время работы O(log n) или ниже), и их скорость работы обычно напрямую зависит от N. Тем не менее, множественные улучшения и доработки позволяют добиться достаточного малого времени работы даже при весьма больших объемах словарей.
Существует также еще множество разнообразных и неэффективных методов, основанных, помимо всего прочего, на адаптации различных, уже где-либо применяемых техник и приемов к данной предметной области. В числе таких методов — адаптация префиксных деревьев (Trie) к задачам нечеткого поиска, которую я оставил без внимания в виду её малой эффективности. Но есть и алгоритмы, основанные на оригинальных подходах, например, алгоритм Маасса-Новака, который хоть и имеет сублинейное асимптотическое время работы, но является крайне неэффективным из-за огромных констант, скрывающихся за такой временной оценкой, которые проявляются в виде огромного размера индекса.
Практическое использование алгоритмов нечеткого поиска в реальных поисковых системах тесно связано с фонетическими алгоритмами, алгоритмами лексического стемминга — выделения базовой части у различных словоформ одного и того же слова (например, такую функциональность предоставляют Snowball и Яндекс mystem), а также с ранжированием на основе статистической информации, либо же с использованием сложных изощренных метрик.
По ссылке http://code.google.com/p/fuzzy-search-tools можно найти мои реализации на Java:
- Расстояние Левенштейна (с отсечением и префиксным вариантом);
- Расстояние Дамерау-Левенштейна (с отсечением и префиксным вариантом);
- Алгоритм Bitap (Shift-OR / Shift-AND с модификациями Wu-Manber);
- Алгоритм расширения выборки;
- Метод N-грамм (оригинальный и с модификациями);
- Метод хеширования по сигнатуре;
- BK-деревья.
Стоит заметить, что в процессе изучения этой темы у меня появились кое-какие собственные наработки, позволяющие на порядок сократить время поиска за счет умеренного увеличения размера индекса и некоторого ограничения в свободе выбора метрик. Но это уже совсем другая история.
Ссылки:
- Исходные коды к статье на Java. http://code.google.com/p/fuzzy-search-tools
- Расстояние Левенштейна. http://ru.wikipedia.org/wiki/Расстояние_Левенштейна
- Расстояние Дамерау-Левенштейна. http://en.wikipedia.org/wiki/Damerau–Levenshtein_distance
- Хорошее описание Shift-Or c модификациями Wu-Manber, правда, на немецком. http://de.wikipedia.org/wiki/Baeza-Yates-Gonnet-Algorithmus
- Метод N-грамм. http://www.cs.helsinki.fi/u/ukkonen/TCS92.pdf
- Хеширование по сигнатуре. http://itman.narod.ru/articles/rtf/confart.zip
- Сайт Леонида Моисеевича Бойцова, целиком посвященный нечеткому поиску. http://itman.narod.ru/
- Реализация Shift-Or и некоторых других алгоритмов. http://johannburkard.de/software/stringsearch/
- Fast Text Searching with Agrep (Wu & Manber). http://www.at.php.net/utils/admin-tools/agrep/agrep.ps.1
- Damn Cool Algorithms — автомат Левенштейна, BK-деревья, и еще кое-какие алгоритмы. http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
- BK-деревья на Java. http://code.google.com/p/java-bk-tree/
- Алгоритм Маасса-Новака. http://yury.name/internet/09ia-seminar.ppt
- Библиотека метрик SimMetrics. http://staffwww.dcs.shef.ac.uk/people/S.Chapman/simmetrics.html
- Библиотека метрик SecondString. http://sourceforge.net/projects/secondstring/
English version: Fuzzy string search