Сегодня на Хабре появилась очень интересная статья, о поиске минимального (максимального) значения на отрезке в массиве. Так как статья оказалось интересной и популярной, я решил с вами поделиться ещё одним алгоритмом поиска в массиве некоторых «специальных» значений.
Наверняка каждому встречалась задача нахождения k-ого наименьшего элемента в массиве. k-ый элемент характеризуется тем, что он больше (или равен) k элементов массива и меньше или равен N-k оставшихся элементов (где N – число элементов в массиве).
Задача нахождения k-ого наименьшего элемента обычно связывается с задачей сортировки, так как очевидный метод нахождения этого элемента состоит в сортировке N элементов и выборе k-ого.
Но мы с вами пойдём немного другим путём. Я предполагаю, что читатели знают, как работает алгоритм быстрой сортировки, но на всякий случай напомню. В массиве выбирается случайный элемент x, и выполнется просмотр массива слева, пока не найдётся элемент a[i]>x, затем выполняется просмотр справа, пока не будет найден элемент a[j]<x. Как только два таких элемента найдены, выполняется их обмен и просмотр продолжается до тех пор, пока индексы i,j не станут равны где-то в середине массива. В результате получается массив левая часть которого содержит элементы <=x, а правая часть содержит элементы >=x. Описанная процедура применяется рекурсивно для левой и правой части и продолжается до тех пор, пока не будет получен полностью отсортированный массив. (Немного подробнее о эффективных алгоритмах сортировки).
Процедура разделения, используемая в быстрой сортировке, даёт потенциальную возможность находить искомый (k-ый) элемент гораздо быстрее.
Этот алгоритм работает следующим образом. На первом шаге вызывается процедура разделения с L=1 и R=N (т.е. разделение выполняется для всего массива), причём в качестве разделяющего значения x выбирается a[k]. После разделения получаются значения индексов i,j такие, что
a[h]<x для всех h<i
a[h]>x для всех h>j
i>j
Здесь возможны три случая:
•Разделяющее значение x оказалось слишком мало. В результате граница между двумя частями меньше нужного значения k. Тогда операцию разделения нужно повторить с элементами a[i]…a[R].

•Выбранное значение x оказалось слишком велико. Тогда операцию разделения нужно повторить с элементами a[L]…a[j].
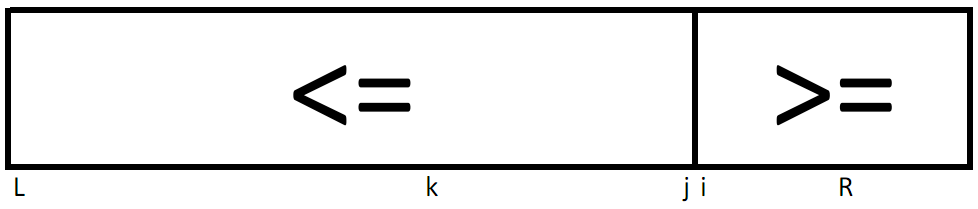
•Элемент a[k] разбивает массив на две части в нужной пропорции и поэтому является искомым значением.

Операцию разделения нужно повторять, пока не реализуется случай 3. Этот цикл выражается следующим фрагментом (прошу прощения за Pascal, но мои ученики пока знают только его):
Если предположить, что в среднем каждое разбиение делит пополам размер части массива, в которой находится искомое значение, то необходимое число сравнений будет N+N/2+N/4+…+1=2N. Это объясняет эффективность приведённой процедуры для поиска медиан и прочих величин, а также объясняет её превосходство над простым методом, состоящем в предварительной сортировке всего массива с последующим выбором k-ого элемента (где наилучшее поведение имеет порядок N*log(N)).
Надеюсь, этот алгоритм поможет вам сделать ваши программы более эффективными и быстрыми. Спасибо за внимание.
Наверняка каждому встречалась задача нахождения k-ого наименьшего элемента в массиве. k-ый элемент характеризуется тем, что он больше (или равен) k элементов массива и меньше или равен N-k оставшихся элементов (где N – число элементов в массиве).
Задача нахождения k-ого наименьшего элемента обычно связывается с задачей сортировки, так как очевидный метод нахождения этого элемента состоит в сортировке N элементов и выборе k-ого.
Но мы с вами пойдём немного другим путём. Я предполагаю, что читатели знают, как работает алгоритм быстрой сортировки, но на всякий случай напомню. В массиве выбирается случайный элемент x, и выполнется просмотр массива слева, пока не найдётся элемент a[i]>x, затем выполняется просмотр справа, пока не будет найден элемент a[j]<x. Как только два таких элемента найдены, выполняется их обмен и просмотр продолжается до тех пор, пока индексы i,j не станут равны где-то в середине массива. В результате получается массив левая часть которого содержит элементы <=x, а правая часть содержит элементы >=x. Описанная процедура применяется рекурсивно для левой и правой части и продолжается до тех пор, пока не будет получен полностью отсортированный массив. (Немного подробнее о эффективных алгоритмах сортировки).
Процедура разделения, используемая в быстрой сортировке, даёт потенциальную возможность находить искомый (k-ый) элемент гораздо быстрее.
Этот алгоритм работает следующим образом. На первом шаге вызывается процедура разделения с L=1 и R=N (т.е. разделение выполняется для всего массива), причём в качестве разделяющего значения x выбирается a[k]. После разделения получаются значения индексов i,j такие, что
a[h]<x для всех h<i
a[h]>x для всех h>j
i>j
Здесь возможны три случая:
•Разделяющее значение x оказалось слишком мало. В результате граница между двумя частями меньше нужного значения k. Тогда операцию разделения нужно повторить с элементами a[i]…a[R].

•Выбранное значение x оказалось слишком велико. Тогда операцию разделения нужно повторить с элементами a[L]…a[j].
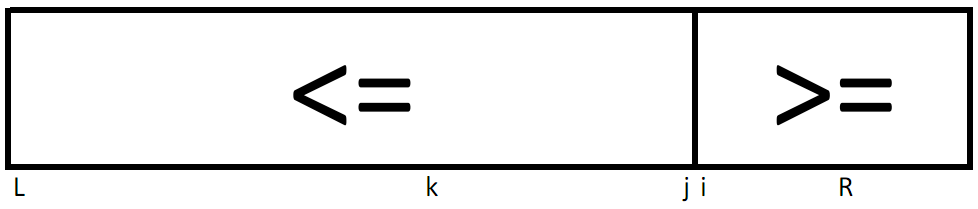
•Элемент a[k] разбивает массив на две части в нужной пропорции и поэтому является искомым значением.

Операцию разделения нужно повторять, пока не реализуется случай 3. Этот цикл выражается следующим фрагментом (прошу прощения за Pascal, но мои ученики пока знают только его):
- procedure Find(k: integer);
- var
- L,R,i,j: integer;
- w,x: integer;
- begin
- L:=1; R:=N;
- while L<R-1 do
- begin
- x:=a[k];
- i:=L;
- j:=R;
- REPEAT
- while a[i]<x do
- i:=i+1;
- while x<a[j] do
- j:=j-1;
- if i<=j then
- begin
- w:=a[i];
- a[i]:=a[j];
- a[j]:=w;
- i:=i+1;
- j:=j-1;
- end;
- UNTIL i>j;
- if j<k then
- L:=i;
- if k<i then
- R:=j;
- end;
- end;
Если предположить, что в среднем каждое разбиение делит пополам размер части массива, в которой находится искомое значение, то необходимое число сравнений будет N+N/2+N/4+…+1=2N. Это объясняет эффективность приведённой процедуры для поиска медиан и прочих величин, а также объясняет её превосходство над простым методом, состоящем в предварительной сортировке всего массива с последующим выбором k-ого элемента (где наилучшее поведение имеет порядок N*log(N)).
Надеюсь, этот алгоритм поможет вам сделать ваши программы более эффективными и быстрыми. Спасибо за внимание.