
Некоторое время назад я сходил на собеседование в одну довольно большую и уважаемую компанию. Собеседование прошло хорошо и понравилось как мне, так и, надеюсь, людям его проводившим. Но на следующий день, в процессе разбора полетов, я обнаружил, что в ходе собеседования ответ на как минимум один вопрос был неверен.
Вопрос: Почему поиск в python dict на больших объемах данных быстрее чем итерация по индексированному массиву?
Ответ: В dict хранятся хэши от ключей. Каждый раз, когда мы ищем в dict значение по ключу, мы сначала вычисляем его хэш, а потом (внезапно), выполняем бинарный поиск. Таким образом, сложность составляет O(lg(N))!
На самом деле никакого бинарного поиска тут нет. И сложность алгоритма не O(lg(N)), а Amort. O(1) — так как в основе dict питона лежит структура под названием Hash Table.
Причиной неверного ответа было то, что я не удосужился досконально изучить те структуры, которые лежат в основе работы с коллекциями моего любимого языка. Правда, по результатам опроса нескольких знакомых разработчиков, оказалось что это не только моя проблема, очень многие вообще не задумываются, как работают коллекции в их любимых ЯП. А ведь используем мы их каждый день и не по разу. Так родилась идея этой статьи.
Пара слов о классификации структур в статье. Если вы изучите источники, которые перечислены в списке использованной информации, то заметите, что классификация в данной статье не соответствует классификации ни в одном из источников (в некоторых источниках ее нет вовсе). Это вызвано тем, что мне показалось более целесообразным рассматривать структуры в контексте их использования. Например ассоциативный массив в PHP/Python/С++ или список в .Net/Python.
Итак, поехали.
1. Array — он же индексированный массив.
Array — это коллекция фиксированного размера, состоящая из элементов одинакового типа.
Интерфейс:
- get_element_at(i): сложность O(1)
- set_element_at(i, value): сложность O(1)
Поиск в массиве осуществляется путем перебора элементов по индексам => сложность O(N).
Почему время доступа к элементу по индексу постоянно? Массив состоит из элементов одного типа, имеет фиксированный размер и располагается в непрерывной области памяти => чтобы получить j-й элемент массива, нам достаточно взять указатель на начало массива и прибавить к нему размер элемента умноженный на его индекс. Результат этого несложного вычисления будет указывать как раз на искомый элемент массива.
*aj = beginPointer + elementSize*j-1
Примеры:
с/с++: int i_array[10];
java/C#: int[10] i_array;
Python: array.array
php: SplFixedArray
2. List (список).
List — это список элементов произвольного типа переменной длины (то есть мы можем в любой момент добавить элемент в список или удалить его). Список позволяет перебирать элементы, получать элементы по индексу, а так же добавлять и удалять элементы. Реализации у List возможны разные, основные — это (Single/Bidirectional) Linked List и Vector. Классический List предоставляет возможность работы с ним напрямую и через итератор, интерфейсы обоих классов рассмотрим ниже.
Интерфейс List :
- prepend(item): Добавить элемент в начало списка.
- append(item): Добавить элемент в конец списка.
- insert_after(List Iterator, item): Добавить элемент после текущего.
- remove_firts(): Удалить первый элемент.
- remove_after(List Iterator): Удалить элемент после текущего.
- is_empty(): Пуст ли List.
- get_size(): Возвращает размер списка.
- get_nth(n): Вернуть n-й элемент.
- set_nth(n, value): Задать значение n-му элементу.
Интерфейс List Iterator:
- get_value(): получить значение текущего элемента.
- set_value(): задать значение текущему элементу.
- move_next(): переместиться к следующему элементу.
- equal(List Iterator): проверяет — ссылается ли другой итератор на тот же элемент списка.
Надо отметить, что в некоторых (в основном интерпретируемых), языках программирования эти два интерфейса «склеены» и «обрезаны». Например в python объект типа list можно итерировать, но у него же можно и получить значение обратившись непосредственно по индексу.
Перейдем к реализациям списка.
2.1 Single Linked List

Однонаправленный связный список (односвязный список) представляет из себя цепочку контейнеров. Каждый контейнер содержит внутри себя ссылку на элемент и ссылку на следующий контейнер, таким образом, мы всегда можем переместиться по односвязному списку вперед и всегда можем получить значение текущего элемента. Контейнеры могут располагаться в памяти как им угодно => добавление в односвязный список нового элемента тривиально.
Стоимость операций:
- prepend: O(1)
- insert_after: O(1)
- remove_first/remove_after: O(1)
- get_nth/set_nth: O(N)
Примеры:
с/с++: std::list //Bidirectional Linked List
Java: java.util.LinkedList
c#: System.Collection.Generic.LinkedList //Bidirectional Linked List
php: SplDoublyLinkedList // Bidirectional Linked List
Bidirectional Linked List мы подробно рассматривать не будем, вся разница между ним и Single Linked List заключается в том, что в контейнерах есть ссылка не только на следующий, но и на предыдущий контейнер, что позволяет перемещаться по списку не только вперед, но и назад.
2.2 Vector
Vector — это реализация List через расширение индексированного массива.
Стоимость операций:
- prepend: O(N)
- append: Amort.O(1)
- insert_after: O(N)
- remove_first/remove_after: O(1)
- get_nth/set_nth: O(1)
Очевидно, что главное преимущество Vector'а — быстрый доступ к элементам по индексу, унаследовано им от обычного индексированного массива. Итерировать Vector так же достаточно просто, достаточно увеличивать некий счетчик на единицу и осуществлять доступ по индексу. Но за скорость доступа к элементам приходиться платить временем их добавления. Для того чтобы вставить элемент в середину Vector'a (insert-after) необходимо скопировать все элементы между текущим положением итератора и концом массива, как следствие время доступа в среднем O(N). То же и с удалением элемента в середине массива, и с добавлением элемента в начало массива. Добавление элемента в конец массива при этом может быть выполнено за O(1), но может и не быть — если опять таки потребуется копирование массива в новый, потому говорится, что добавление элемента в конец Vector'а происходит за Amort. O(1).
Примеры:
с/с++: std::vector
Java: java.util.ArrayList
C#: System.Collections.ArrayList, System.Collections.List
Python: list
3. Ассоциативный массив(Словарь/Map)
Коллекция пар ключ=>значение. Элементы (значения) могут быть любого типа, ключи обычно только строки/целые числа, но в некоторых реализация диапазон объектов, которые могут быть использованы в качестве ключа, может быть шире. Размер ассоциативного массива можно изменять путем добавления/удаления элементов.
Интерфейс:
- add(key, value) — добавить элемент
- reassign(key, value) — заменить элемент
- delete(key) — удалить элемент
- lookup(key) — найти элемент
Существует две основные реализации Ассоциативного массива: HashMap и Binary Tree.
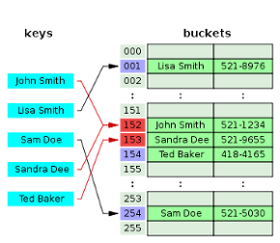
3.1 Hash Table

Как можно догадаться из названия, тут используются хэши. Механика работы Hash Table следующая: в основе лежит все тот же индексированный массив, в котором индексом работает значение хэша от ключа, а значением — ссылка на объект, содержащий ключ и хранимый элемент (bucket). При добавлении элемента — хэш функция вычисляет хэш от ключа и сохраняет ссылку на добавляемый элемент в ячейку массива с соответствующим индексом. Для получения доступа к элементу мы опять таки берем хэш от ключа и, работая так же как с обычным массивом получаем ссылку на элемент.
Пытливый читатель может заметить некоторые проблемы, характерные для реализации этой СД.
- Если хэш от ключа равен например 1928132371827612 — это ведь будет означать, что нам надо иметь массив соответствующего размера? А если у нас в нем всего 2 элемента?
- А если у нас хэши от двух разных ключей совпадут?
Эти две проблемы связаны: очевидно, что мы не можем вычислять длинные хэши, если хотим хранить небольшое количество элементов — это приведет к неоправданым затратам памяти, потому хэш функция обычно выглядти как то так:
index = f(key, arrayLength)
То есть, кроме значения ключа, она так же получает текущий размер массива, это необходимо для определения длины хэша: если мы храним всего 3 элемента — нет смысла делать хэш длиной в 32 разряда. Обратная сторона такого поведения хэш функции — возможность коллизий. Коллизии на самом деле характерны для Hash Table, и существует два метода их разрешения:
Chaining:

Каждая ячейка массива H является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.
Open addressing:
В массиве H хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива H в некотором порядке до тех пор, пока не будет найдена первая свободная ячейка, в которую и будет записан новый элемент. Этот порядок вычисляется на лету, что позволяет сэкономить на памяти для указателей, требующихся в хеш-таблицах с цепочками.
Стоимость операций:
- add: Amort.O(1)/O(N)
- reasign: Amort.O(1)/O(N)
- delete: Amort.O(1)/O(N)
- lookup: Amort.O(1)/O(N)
Здесь первое значение — средняя сложность, второе — сложность выполнения операции в худшем случае. Такая разница обусловлена следующим: при добавлении элемента, в случае если массив заполнен, может понадобиться перестроить Hash Table целиком. При поиске элемента может оказаться так, что мы наткнемся на длинную цепочку коллизий, и опять же будем вынуждены перебрать все элементы.
Примеры:
c++: за исключением QHash автору не известныboost::unordered_map/boost::unordered_set (by NickLion)
java: java.util.HashMap<K,V>
c#: System.Collections.Hashtable, System.Collections.Dictionary<K, V>
python: dict
php: array()
3.2 Binary Tree
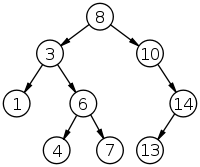
На самом деле не просто Binary Tree, а Self-balancing Binary Tree. Причем следует отметить, что существует несколько различных деревьев, которые могут быть использованы для реализации Ассоциативного массива: red-black tree, AVL-tree и т.д. Мы не будем рассматривать каждое из этих деревьев в деталях, так как это возможно тема еще одной, отдельной статьи, а может и нескольких (если изучать деревья особо тщательно). Опишем только общие принципы.
Определение: двоичное дерево — древовидная структура данных в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. В случае, если у узла нет наследников — он называется листовым узлом.
Для примера возьмем поисковое бинарное дерево (binary search tree): каждый узел представляет из себя контейнер, содержащий три элемента: data — собственно привязанные данные (data содержит как собственно элемент, так и значение ключа), left — ссылка на левый нижележащий узел и right — ссылка на правый нижележащий узел. При этом выполняется такое правило: key[left[X]] < key[X] ≤ key[right[X]] — т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого. При поиске элемента мы обходим дерево, каждый раз сравнивая значение нашего ключа с ключом текущего узла, и, по результатам сравнения определяя в которую сторону нам идти. Несложно подсчитать, что сложность такого поиска — стабильно O(lgN). При добавлении нового узла мы выполняем в целом похожую процедуру пока не найдем, куда воткнуть новый элемент. Правда следует отметить то, что такие деревья еще требуется балансировать — но это мы уже опустим. Пытливый читатель сам найдет необходимую информацию, изучив список источников.
Стоимость операций:
- add: Amort.O(lgN)
- reasign: Amort.O(lgN)
- delete: Amort.O(lgN)
- lookup: Amort.O(lgN)
Примеры:
c++: std::map, std::set
java: java.util.TreeMap<K,V>, так же автора мучает подозрение что java.util.Map<K,V> - из той же оперы
c#: автор теряется в догадках :( SortedDictionary(by NickLion)
python: -
php: -
4. Множество (Set).
Множество — это просто реализация абстракции математического множества, т.е. набора уникальных различимых элементов. (спс. danilI)
Примеры:
c++: std::set
java: java.util.Set
C#: System.Collections.HashSet
python: set/frozenset
Сравнительные характеристики структур данных:

Структуры данных в различных языках программирования:

Ссылки:
Data Structures (en)
Структуры Данных (рус)
Binary search tree (en)
Двоичное дерево поиска (рус)
Так же автор заглянул в исходники PHP и почитал доку по STL.
Upd. Да, в питоне есть обычный индексированный массив (array.array). Спасибо enchantner. С поправкой, тип не обязательно числовой, тип можно указывать.
Upd. Сделано много исправлений по тексту. idemura, zibada, tzlom, SiGMan, freeOne, Slaffko, korvindest, Laplace, enchantner спасибо за правки!
Upd.
Из комментариев zibada:
Да, вот как раз из-за отсутствия описания итерации по Map из статьи вообще непонятно, зачем, казалось бы, нужны деревья, когда есть хэши. (O(logN) против O(1)).
Нужны они затем, что перечислять элементы Map (или Set) можно хотеть:
— в любом, негарантированном порядке (HashMap, встроенные хэши в некоторых скриптовых языках);
— в порядке добавления (LinkedHashMap, встроенные хэши в некоторых других скриптовых языках);
— в порядке возрастания ключей + возможность перебрать только ключи в заданном диапазоне.
А вот для последнего случая альтернатива деревьям — только полная сортировка всей коллекции после каждого изменения или перед запросом.
Что долго и печально для больших коллекций, но вполне работает для небольших — поэтому в скриптовые языки деревья особо и не встраивают.