На каждом этапе эксперимента, начиная от подготовки материала, продолжая проведением PCR и заканчивая секвенированием, происходит накопление ошибки. Нам нужен механизм оценки значимости результата. Какова вероятность, что риды, оказавшиеся на некотором участке генома, оказались там неслучайно? Подход, представленный в этой статье, применим для данных, полученных с помощью DNA-seq, и рассказывает о возможности применения распределения Пуассона для оценки значимости.
Эта иллюстрация схематично изображает процесс подготовки материала для секвенирования. На каждом этапе возможна ошибка, в результате дающая рид на произвольном участке генома.
Файл со всеми ридами, которых миллионы в рамках одного секвенирования, передают в программу bowtie, являющуюся на текущий момент самой быстрой. Строка выполнения программы bowtie может быть такой:
Параметры, указанные в примере, характеризуют следующее поведение программы:
-q — обрабатывает входной файл как FASTQ, а не FASTA
-v — количество допустимых ошибок в риде, в вышеприведенном примере их 2
-m — сколько вхождений (ридов) в геноме искать, в данном случае задано 1
-p — сколько threads задействовать, я исходил из количества ядер процессора — 8
-S — означает, что выходной файл будет записан в формате .sam
/usr/src/bowtie-0.12.7/indexes/hg19 — путь к заранее проиндексированному геному, выполненный программой bowtie-build. Также готовый путь можно скачать из интернета.
— (тире в конце второй строки) означает вывод в стандартный output для передачи программе samtools, которая на лету преобразует его в .bam.
В описании я пропустил параметры --best --strata, которые задают специальный режим работы bowtie: если программа находит более чем одно вхождение рида в геноме с разным количеством ошибок, то она выводит результат с наименьшей ошибкой. Если результатов с наименьшей ошибкой больше одного, то они не выводятся. Это увеличивает время работы программы, но в то же время позволяет повысить чувствительность нахождения ридов в геноме. Вот пример вывода .sam/.bam файла:
Шапка (строки, начинающиеся на @SQ, @HD, @PG) содержит описания: имена хромосом и их длины, сортирован ли файл, команда, с помощью которой был получен файл. Тело состоит из строк, каждая строка — это рид, но уже с координатами в геноме. Более детально прочитать можно тут http://genome.sph.umich.edu/wiki/SAM.
Распределение по геному бывает разное, но в обогащенных участках считается, что эксперимент с большей степенью вероятности прошел удачно, если распределение обладает следующими свойствами: even coverage (равномерное покрытие), high complexity (высокая сложность), continuity of coverage (непрерывное покрытие). Примеры, как риды могут покрывают геном, изображены на рисунках сверху.
Для определения обогащенных участков, воспользуемся следующим рассуждением. Сложим все длины хромосом и вычтем длину повторяющихся участков (примерная длина 2282603114 для hg19), примем получившуюся длину за G. Разобьем длину G на окна шириной по W (для примера 500). Примем за N количество получившихся окон (G/W примерно 4565206.228). Подсчитаем количество ридов в эксперименте, которые были удачно найдены в геноме (пусть будет 4E6 из 4.5E6 всего), примем их количество за S. Тогда среднее количество ридов на окно, обозначим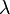
, будет 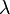=S*W/G=S/N.
Пуассоновское распределение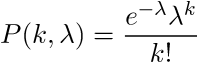
выражает вероятность происхождения заданного числа k событий за промежуток времени при известном среднем происхождении событий. Кумулятивное пуассоновское распределение будет выражать вероятность происхождения событий численностью до k. Будем использовать кумулятивное распределение, так как нас интересует вероятность того, что кол-во ридов в окне меньше k. Нулевая гипотеза: k ридов в окне случайно. Альтернативная гипотеза: k ридов в окне не случайно. Вероятность того, что наша нулевая гипотеза верна ровна 
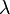. Чем ближе P(k,) к 0, тем меньше вероятность, что риды попали в заданное окно случайно. В нашем примере получаем, что, если количество ридов в окне до 15, то 1-P(15,0.876193)=2.55351E-15, т.е. в окно шириной 500 количество ридов до 15 может попасть случайно с вероятностью 2.55351E-15. Это число ещё называют p value. Следовательно, если ридов больше 15, то они с ещё меньшей вероятностью попадают в окно случайно. Таким образом, в программе можно задать условие: если p value < = 1.e16, значит данные, попавшие в окно, следует оставить для рассмотрения, остальные — отбросить.
Ниже приводится пример программы, которая использует часть классов, описанных в предыдущей статье, и дополняется новым классом PoissonHandler. Дополнительные файлы к первому архиву можно скачать тут. В новой директории poisson набираем qmake, затем make. Собранная программа poisson строит таблицу значимости для окон в 500bp, расположенных за транскрипционным старт-сайтом каждого гена, аннотация выбирается из геном браузера. Более детальную работу с геном браузером рассмотрим в другой статье. Далее выбираются риды из .bam файла, попавшие в наши окна, для них строится пуассоновское распределение. Результат записывается в файл.
PoissonHandler.hpp
PoissonHandler.cpp
Эти небольшие алгоритмы в дальнейшем пригодятся для реализации более сложных, например, таких как ZINBA или SICER. О них мы поговорим в другой статье. Часто задача состоит в нахождении обогащенных участков без использования аннотации. И тогда шаг за шагом нужно отбирать данные, попавшие в окна и прошедшие через фильтр.
Comprehensive comparative analysis of strand-specific RNA sequencing methods
Nat Methods. 2010 September; 7(9): 709–715.
Joshua Z. Levin,1,6 Moran Yassour,1,2,3,6 Xian Adiconis,1 Chad Nusbaum,1Dawn Anne Thompson,1 Nir Friedman,3,4 Andreas Gnirke,1 and Aviv Regev1,2,5
www.ncbi.nlm.nih.gov/pmc/articles/PMC3005310
Genomic Location Analysis by ChIP-Seq
J Cell Biochem. 2009 May 1;107(1):11-8.
Artem Barski* and Keji Zhao*
Laboratory of Molecular Immunology, National Heart, Lung and Blood Institute, NIH, Bethesda, MD 20892
www.ncbi.nlm.nih.gov/pubmed/19173299
An integrated strategy for identification of both sharp and broad peaks from next-generation sequencing data.
Genome Biol. 2011 Jul 25;12(7):120.
Peng W, Zhao K.
Department of Physics, The George Washington University, 725 21st Street NW, Washington, DC 20052, USA. wpeng@gwu.edu
www.ncbi.nlm.nih.gov/pubmed/21787381
A clustering approach for identification of enriched domains from histone modification ChIP-Seq data.
Bioinformatics. 2009 Aug 1;25(15):1952-8. Epub 2009 Jun 8.
Zang C, Schones DE, Zeng C, Cui K, Zhao K, Peng W.
Department of Physics, The George Washington University, Washington, DC 20052, USA.
www.ncbi.nlm.nih.gov/pubmed/19505939
ZINBA integrates local covariates with DNA-seq data to identify broad and narrow regions of enrichment, even within amplified genomic regions.
Genome Biol. 2011 Jul 25;12(7):R67.
Rashid NU, Giresi PG, Ibrahim JG, Sun W, Lieb JD.
Department of Biostatistics, Gillings School of Global Public Health, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA.
www.ncbi.nlm.nih.gov/pubmed/21787385
Review is prepared by Andrey Kartashov, Cincinnati OH, mail: porter@porter.st
Эта иллюстрация схематично изображает процесс подготовки материала для секвенирования. На каждом этапе возможна ошибка, в результате дающая рид на произвольном участке генома.
- А.1 Клетка с ДНК обрабатывается формальдегидом для лучшего закрепления белка. Потом ДНК режется на фрагменты различными способами, в том числе ультразвуком.
- А.2-3 Добавляется антитело, которое чувствительно к белкам. Фрагменты отмеченные белком скрепляются с антителом. Некоторые фрагменты соединяются случайным образом.
- А.4 Происходит осаждение антител с фрагментами ДНК. Очистка фрагментов ДНК от антител и белков.
- B.1-4 Эти пункты показывают шаги по подготовке полученных фрагментов ДНК для секвенирования. Добавление специальных адаптеров. Умножение с помощью PCR. Размещение на слайде.
@HWI-XXXXX_0470:1:1:1761:946#0/1
NCCCTTTGGATTTGTCCTTTCAGATGCATTAGCCAT
+HWI-XXXXX_0470:1:1:1761:946#0/1
BKNNJMHHEJRTRRR_______________Y[[[Y_
Файл со всеми ридами, которых миллионы в рамках одного секвенирования, передают в программу bowtie, являющуюся на текущий момент самой быстрой. Строка выполнения программы bowtie может быть такой:
/usr/src/bowtie-0.12.7/bowtie -q -v 2 -m 1 --best --strata -p 8 -S \
/usr/src/bowtie-0.12.7/indexes/hg19 - |
samtools view -Sb - >${DIRNAME}/${SEQNAME}.bam
Параметры, указанные в примере, характеризуют следующее поведение программы:
-q — обрабатывает входной файл как FASTQ, а не FASTA
-v — количество допустимых ошибок в риде, в вышеприведенном примере их 2
-m — сколько вхождений (ридов) в геноме искать, в данном случае задано 1
-p — сколько threads задействовать, я исходил из количества ядер процессора — 8
-S — означает, что выходной файл будет записан в формате .sam
/usr/src/bowtie-0.12.7/indexes/hg19 — путь к заранее проиндексированному геному, выполненный программой bowtie-build. Также готовый путь можно скачать из интернета.
— (тире в конце второй строки) означает вывод в стандартный output для передачи программе samtools, которая на лету преобразует его в .bam.
В описании я пропустил параметры --best --strata, которые задают специальный режим работы bowtie: если программа находит более чем одно вхождение рида в геноме с разным количеством ошибок, то она выводит результат с наименьшей ошибкой. Если результатов с наименьшей ошибкой больше одного, то они не выводятся. Это увеличивает время работы программы, но в то же время позволяет повысить чувствительность нахождения ридов в геноме. Вот пример вывода .sam/.bam файла:
@HD VN:1.0 SO:unsorted
@SQ SN:chr10 LN:135374737
@SQ SN:chr11 LN:134452384
…
@PG ID:Bowtie VN:0.12.7 CL:"/usr/src/bowtie-0.12.7/bowtie -q -v 1 -m 1 --best --strata -p 8 -S"
USI-EAS21_8_3445_7_1_452_540 0 chr5 39195556 255 23M * 0 0 CTCCAGATTCTCTGGAAAGATGG SSSSSSPSSSSSSSSGNNSJSSL XA:i:0 MD:Z:23 NM:i:0
USI-EAS21_8_3445_7_1_170_242 0 chr14 73509925 255 23M * 0 0 CTGCATTAGACCTAGGCTTAGAA SSSSSSSSSSSSSSSSSSSGSNN XA:i:0 MD:Z:23 NM:i:0
USI-EAS21_8_3445_7_1_290_985 0 chr7 142613233 255 23M * 0 0 AGCTGACTGGCAAGCAACAGAGT JSSSSSSSSSSSPSSGSSLSNSL XA:i:0 MD:Z:23 NM:i:0
USI-EAS21_8_3445_7_1_881_711 4 * 0 0 * * 0 0 ATCGGAAGAGCTCGTATGCCGTC SSSSPSSSSSSSSSSSSSSSSNS XM:i:0
USI-EAS21_8_3445_7_1_897_318 0 chr3 50101427 255 23M * 0 0 GGGCGCAGAACCGCTGCTGCTGC SPSSSSSSSPPSSSSNSPPPLSL XA:i:1 MD:Z:15A7NM:i:1
Шапка (строки, начинающиеся на @SQ, @HD, @PG) содержит описания: имена хромосом и их длины, сортирован ли файл, команда, с помощью которой был получен файл. Тело состоит из строк, каждая строка — это рид, но уже с координатами в геноме. Более детально прочитать можно тут http://genome.sph.umich.edu/wiki/SAM.
Распределение по геному бывает разное, но в обогащенных участках считается, что эксперимент с большей степенью вероятности прошел удачно, если распределение обладает следующими свойствами: even coverage (равномерное покрытие), high complexity (высокая сложность), continuity of coverage (непрерывное покрытие). Примеры, как риды могут покрывают геном, изображены на рисунках сверху.
Для определения обогащенных участков, воспользуемся следующим рассуждением. Сложим все длины хромосом и вычтем длину повторяющихся участков (примерная длина 2282603114 для hg19), примем получившуюся длину за G. Разобьем длину G на окна шириной по W (для примера 500). Примем за N количество получившихся окон (G/W примерно 4565206.228). Подсчитаем количество ридов в эксперименте, которые были удачно найдены в геноме (пусть будет 4E6 из 4.5E6 всего), примем их количество за S. Тогда среднее количество ридов на окно, обозначим
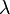, будет 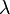=S*W/G=S/N.Пуассоновское распределение
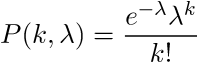выражает вероятность происхождения заданного числа k событий за промежуток времени при известном среднем происхождении событий. Кумулятивное пуассоновское распределение будет выражать вероятность происхождения событий численностью до k. Будем использовать кумулятивное распределение, так как нас интересует вероятность того, что кол-во ридов в окне меньше k. Нулевая гипотеза: k ридов в окне случайно. Альтернативная гипотеза: k ридов в окне не случайно. Вероятность того, что наша нулевая гипотеза верна ровна 
. Чем ближе P(k,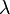) к 0, тем меньше вероятность, что риды попали в заданное окно случайно. В нашем примере получаем, что, если количество ридов в окне до 15, то 1-P(15,0.876193)=2.55351E-15, т.е. в окно шириной 500 количество ридов до 15 может попасть случайно с вероятностью 2.55351E-15. Это число ещё называют p value. Следовательно, если ридов больше 15, то они с ещё меньшей вероятностью попадают в окно случайно. Таким образом, в программе можно задать условие: если p value < = 1.e16, значит данные, попавшие в окно, следует оставить для рассмотрения, остальные — отбросить.Ниже приводится пример программы, которая использует часть классов, описанных в предыдущей статье, и дополняется новым классом PoissonHandler. Дополнительные файлы к первому архиву можно скачать тут. В новой директории poisson набираем qmake, затем make. Собранная программа poisson строит таблицу значимости для окон в 500bp, расположенных за транскрипционным старт-сайтом каждого гена, аннотация выбирается из геном браузера. Более детальную работу с геном браузером рассмотрим в другой статье. Далее выбираются риды из .bam файла, попавшие в наши окна, для них строится пуассоновское распределение. Результат записывается в файл.
PoissonHandler.hpp
#ifndef PoissonHandler_H
#define PoissonHandler_H
#include <config.hpp>
class PoissonHandler : public QState
{
Q_OBJECT
private:
GenomeDescription *sql_input;
GenomeDescription *sam_input;
QSettings setup;
public:
PoissonHandler(GenomeDescription *sql,GenomeDescription *sam,HandledData &output,QState *parent=0);
~PoissonHandler();
protected:
virtual void onEntry(QEvent* event);
};
#endif //
PoissonHandler.cpp
#include "PoissonHandler.hpp"
//-------------------------------------------------------------
//-------------------------------------------------------------
PoissonHandler::~PoissonHandler()
{
}
//-------------------------------------------------------------
//-------------------------------------------------------------
PoissonHandler::PoissonHandler(GenomeDescription *sql,GenomeDescription *sam,HandledData &,QState * parent):
QState(parent),
sql_input(sql),
sam_input(sam)
{
}
//-------------------------------------------------------------
//-------------------------------------------------------------
void PoissonHandler::onEntry(QEvent*)
{
if(!setup.contains("AvgTagWindow"))
setup.setValue("AvgTagWindow",500);
if(!setup.contains("siteShift"))
setup.setValue("siteShift",75);
qint32 window=setup.value("AvgTagWindow").toInt();
qint32 half_window=0;//window/2;
qint32 shift=setup.value("siteShift").toInt();
int c=0;//sense count, even/odd c sense/nonsense
QMap<QString,int> poisson;
QMapIterator<QChar,QMap<QString,QMap<qint32,qint32> > > sense(sql_input->genome);
while(sense.hasNext())
{
sense.next(); c++;
QMapIterator<QString,QMap<qint32,qint32> > dictionary(sense.value());
while(dictionary.hasNext())
{
dictionary.next();
QMapIterator<qint32,qint32> s(dictionary.value()); //sql result for strand+chromosome
if((sam_input->genome['+']).contains(dictionary.key())) //chromosome chr1,chr2...
{
QMapIterator<qint32,qint32> k( (sam_input->genome['+'])[dictionary.key()] );//+ strand,sam file, iteration over strand+chromosome
s.next(); //c++;
k.next();
while (k.hasNext()) // + strand, iteration over strand+chromosome+each position
{
//if align is inside of the segment of the start site
qint32 x1=k.key()- s.key() +half_window +shift;
qint32 x2=x1-window;
if( (x1^x2) < 0 )
{//inside segment
poisson[((sql_input->genome_h[sense.key()])[dictionary.key()])[s.key()]]+=k.value();
k.next();
}
else
{
if((k.key() +shift)>(s.key()+half_window))
{
if(!s.hasNext()) break;
s.next();// c++;
}
else
{
k.next();
}
}
}//while k.hasNext
}//if + strand sam input
if((sam_input->genome['-']).contains(dictionary.key()))
{
QMapIterator<qint32,qint32> j( (sam_input->genome['-'])[dictionary.key()] );//- strand,sam file
s.toFront();
s.next();
j.next();
while (j.hasNext()) // - strand
{
//if align is inside of the segment of the start site
qint32 x1=j.key()- s.key() +half_window -shift;
qint32 x2=x1-window;
if( (x1^x2) < 0 )
{//inside segment
poisson[((sql_input->genome_h[sense.key()])[dictionary.key()])[s.key()]]+=j.value();
j.next();
}
else
{
if((j.key() -shift)>(s.key()+half_window))
{
if(!s.hasNext()) break;
s.next();
}
else
{
j.next();
}
}
}
}//if - strand sam file
}//while dictionary
}//while sense
//Poisson
{
qreal lamda=(qreal)(window*(sam_input->total-sam_input->notAligned))/(sam_input->tot_len*0.741);
QFile _outFile;
_outFile.setFileName(setup.value("outFileName").toString());
_outFile.open(QIODevice::WriteOnly|QIODevice::Truncate);
qreal exp_l=qExp(-lamda);
QString str;
foreach(str,poisson.keys())
{
//P(x,L)=(e**-1)*(L**x)/x!
// qreal pois=exp_l; //qExp(-lamda)*qPow(lamda,poisson[str]);
// for(int i=2; i<= poisson[str];i++)
// pois=pois*lamda/i;
//P(x,L)=(e**-1)*E(1-k)(L**x(i))/x(i)!
qreal pois=exp_l;
qreal delim=1.0;
qreal sum=1.0;
for(int i=1; i<= poisson[str];i++)
{
delim*=lamda/i;
sum+=delim;
}
pois*=sum;
_outFile.write( (QString("%1\t%2\t%3\n").arg(str).arg(poisson[str]).arg(pois,0,'e',20)).toLocal8Bit() );
}
_outFile.flush();
_outFile.close();
}//if(1)
}//end of function
//-------------------------------------------------------------
//-------------------------------------------------------------
Эти небольшие алгоритмы в дальнейшем пригодятся для реализации более сложных, например, таких как ZINBA или SICER. О них мы поговорим в другой статье. Часто задача состоит в нахождении обогащенных участков без использования аннотации. И тогда шаг за шагом нужно отбирать данные, попавшие в окна и прошедшие через фильтр.
Comprehensive comparative analysis of strand-specific RNA sequencing methods
Nat Methods. 2010 September; 7(9): 709–715.
Joshua Z. Levin,1,6 Moran Yassour,1,2,3,6 Xian Adiconis,1 Chad Nusbaum,1Dawn Anne Thompson,1 Nir Friedman,3,4 Andreas Gnirke,1 and Aviv Regev1,2,5
www.ncbi.nlm.nih.gov/pmc/articles/PMC3005310
Genomic Location Analysis by ChIP-Seq
J Cell Biochem. 2009 May 1;107(1):11-8.
Artem Barski* and Keji Zhao*
Laboratory of Molecular Immunology, National Heart, Lung and Blood Institute, NIH, Bethesda, MD 20892
www.ncbi.nlm.nih.gov/pubmed/19173299
An integrated strategy for identification of both sharp and broad peaks from next-generation sequencing data.
Genome Biol. 2011 Jul 25;12(7):120.
Peng W, Zhao K.
Department of Physics, The George Washington University, 725 21st Street NW, Washington, DC 20052, USA. wpeng@gwu.edu
www.ncbi.nlm.nih.gov/pubmed/21787381
A clustering approach for identification of enriched domains from histone modification ChIP-Seq data.
Bioinformatics. 2009 Aug 1;25(15):1952-8. Epub 2009 Jun 8.
Zang C, Schones DE, Zeng C, Cui K, Zhao K, Peng W.
Department of Physics, The George Washington University, Washington, DC 20052, USA.
www.ncbi.nlm.nih.gov/pubmed/19505939
ZINBA integrates local covariates with DNA-seq data to identify broad and narrow regions of enrichment, even within amplified genomic regions.
Genome Biol. 2011 Jul 25;12(7):R67.
Rashid NU, Giresi PG, Ibrahim JG, Sun W, Lieb JD.
Department of Biostatistics, Gillings School of Global Public Health, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA.
www.ncbi.nlm.nih.gov/pubmed/21787385
Review is prepared by Andrey Kartashov, Cincinnati OH, mail: porter@porter.st