
Преобразование Хафа служит для поиска на изображении фигур, заданных аналитически: прямых, окружностей и любых других, для которых вы сможете придумать уравнение с небольшим количеством параметров. О преобразовании Хафа написано немало, и данная статья не ставит цели подробно осветить все аспекты. Я лишь объясню общий принцип, останавливаясь на особенностях, мешающих его реализации на GPU «в лоб» и, конечно же, предложу решение. Те, кто знают проблемы и хотят сразу видеть решение, могут пропустить пару-тройку разделов.
Алгоритм для CPU
Сначала описываем искомую фигуру уравнением. Например, для линии это может быть y = Ax + B.
Затем заводим так называемый аккумулятор: массив с количеством измерений равным количеству параметров в уравнении. В нашем случае – двумерный. Он у нас будет Пространством Хафа (по крайней мере, его частью) – в нем прямые будут представлены своими параметрами. Например, A – по горизонтали и B – по вертикали. Одна прямая в обычном пространстве = одна точка в пространстве Хафа.
Исходное изображение бинаризируем, и для каждой непустой точки (x0, y0) определяем множество прямых, которые через эту точку могут проходить: y0=Ax0 + B. Тут x0 и y0 – постоянные, A и B переменные, и это уравнение определяет прямую в пространстве Хафа. Эту прямую нам нужно «нарисовать» в нашем аккумуляторе – добавить по 1 к каждому элементу, через который она проходит. Такая процедура называется голосованием: точка голосует за те прямые, которые могут через нее проходить.
В итоге получается, что в аккумуляторе собраны все голоса ото всех точек, и можно считать, что «победители голосования» присутствуют на исходном изображении. Тут, конечно, можно и нужно применять пороговую фильтрацию и другие методы для того, чтобы найти максимумы в пространстве Хафа, но основное и наиболее трудоемкое занятие – это именно наполнение аккумулятора.
Иллюстрация из википедии:
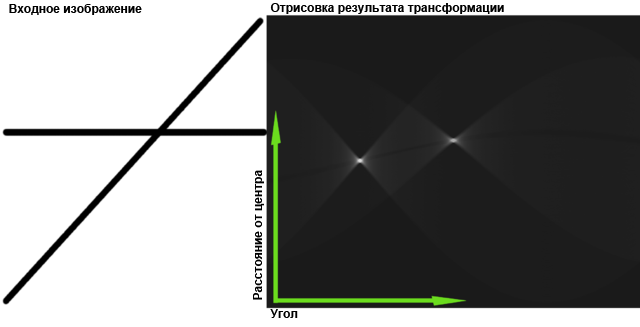
Проблемы с GPU
GPU можно рассматривать как множество (до тысяч) маленьких процессоров, имеющих общую память, и, обычно, алгоритмы делят просто: выделяя каждому процессору свой кусочек работы. Казалось бы, делим исходное изображение на кусочки, даем каждому процессору свой кусочек – и готово. Но нет, мы не можем разделить аккумулятор: в каждом кусочке исходного изображения могут оказаться точки проецирующиеся на любое место пространства Хафа. Писать в общую память процессоры не могут, только читать – иначе будут проблемы с синхронизацией. Выходом было бы дать каждому процессору свой аккумулятор, а после обработки просуммировать аккумуляторы между собой. Но, вы помните, процессоров тысячи. Если даже и найдется столько памяти, время на ее выделение и обработку перекроет выгоды от параллельного выполнения алгоритма.
Другая, меньшая, проблема – алгоритмы «рисования» линий в пространстве Хафа. Они могут быть довольно заковыристыми, но даже самые простые будут содержать циклы и ветвления. А GPU этого не любит: маленькие процессоры не умеют выполнять каждый свою программу, они все выполняют одну (ну не все, но большими группами). Просто каждый оперирует своими данными. Это значит, что выполняются обе ветви ветвления (потом результат ненужной отбрасывается для каждого процессора отдельно). И цикл выполняется столько раз, сколько нужно для наихудшего варианта входных данных. Это ведет к тому, что эффективность использования процессоров падает.
Модификация алгоритма для GPU
Исходная моя идея была такая: почему бы не разделить на «зоны влияния» не исходное изображение, а пространство Хафа? То есть, давайте вычислять значение для каждой точки пространства Хафа отдельно. На первый взгляд, это кажется глупо: любая точка исходного изображения может подать «голос», а, значит, нам придется осмотреть их все. Итого, количество операций чтения = [количество точек исходного изображения] x [количество элементов аккумулятора], тогда как в традиционном способе это лишь [количество точек исходного изображения].
Но зато потенциально уменьшается количество операций записи – [количество элементов аккумулятора] против [количество непустых точек] x [средняя длина образа точки в пространстве Хафа]. Если непустых точек много – разница существенна.
Итого, чтения становится больше, записи меньше, и она становится более упорядоченной. Теперь вспоминаем, в чем еще сила GPU. В скорости чтения! Видеокарты комплектуются быстрой памятью, доступ к ней «спрямлен» до предела — все с целью накладывать текстуры максимально быстро. Правда, это в ущерб латентности – неупорядоченные запросы на чтение выполняются медленнее. Но у нас таких не будет.
Идея вторая. Если уж в пространстве Хафа надо «рисовать» – почему бы не использовать «рисовательные» таланты видеокарт? Давайте наложим исходное изображение на пространство Хафа как текстуру.
Это приводит к тому, что в моем методе не нужны ни код на OpenCL или CUDA, ни шейдеры. Видеокарта даже не обязана их поддерживать, чтобы получить изображение пространства Хафа. Платой за это является неуниверсальность: практически, это два существенно разных метода: один для окружностей и другой, для прямых. Кажется, метод «окружностей» можно применить для любых замкнутых линий и любых фигур с тремя и более параметрами в уравнении, но эффективность может быть разной.
Метод «окружностей»
Окружность описывается уравнением с тремя параметрами – (x-x0)2 + (y-y0)2 = R2. Здесь (x0, y0) – координаты центра, а R – радиус. Пространство Хафа должно иметь три измерения, но мы пока ограничимся двумя и зафиксируем R (допустим, мы его знаем). В этом случае все, что нам нужно найти – это координаты центра(ов).
Возьмем такое исходное изображение (все окружности одного радиуса)

и, сделав почти прозрачным, наложим само на себя следующим образом:

Все изображения смещены от исходного на радиус окружности. Угол между соседними радиусами смещения одинаковый. То есть, допустим, верхние левые углы изображений распределены по окружности того же радиуса, что искомая.
Для наглядности иллюстрации я положил снизу инверсное исходное изображение и отметил важные места красным.
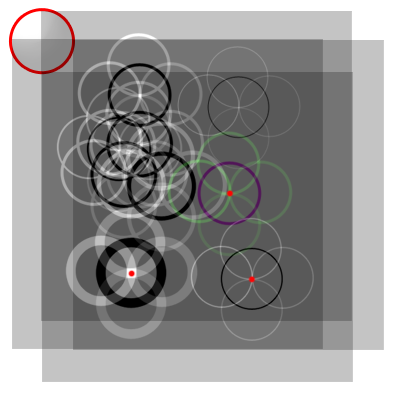
Каждая окружность каждого изображения проходит через центр соответствующей окружности исходного изображения. В этих точках они накладываются друг на друга и получается максимум яркости.
Вот что будет, если проделать эту операцию 32 раза:

И после пороговой фильтрации:

Таким образом, два измерения пространства Хафа мы заполнили. Теперь, варьируя радиус, можно легко заполнить третье. А можно не пытаться накопить все 3 измерения в памяти, а обработать полученную картинку, сохранив положение центров и радиус и освободить память.
Код (Managed DirectX, полная версия – по ссылке ниже), создающий правильно расположенные прямоугольники:
float r = (float)rAbs / targetSize;
for (int i = 0; i < n; i++)
{
double angle = 2 * Math.PI / n * i;
rectangles.Add(new TexturedRect(new Vector2(1f, 1f), new Vector2((float)(Math.Cos(angle) * r), (float)(Math.Sin(angle) * r)), new Vector2(1f, 1f), new Vector2(0f, 0f), 0));
}
Код, устанавливающий альфа-прозрачность правильным образом:
device.RenderState.AlphaBlendEnable = true,
device.RenderState.BlendFactor = (byte)(256.0 * brightness / n)
device.RenderState.BlendOperation = BlendOperation.Add;
device.RenderState.SourceBlend = Blend.BlendFactor;
device.RenderState.DestinationBlend = Blend.One;
Здесь
rAbs задает искомый радиус, brightness – яркость, n – количество слоев.Рендерить все можно в текстуру
new Microsoft.DirectX.Direct3D.Texture(device, targetSize, targetSize, 1, Usage.RenderTarget, cbGray.Checked ? Format.L8 : Format.X8R8G8B8, Pool.Default);
dxPanel.RenderToTexture(new Options()
{
AlphaBlendEnable = true,
BlendFactor = (byte)(256.0 * (tbBrightness.Value / 100.0) / n)
},
rectangles);
А можно использовать 3D текстуру и несколько комплектов слоев для того, чтобы отрендерить все интересующие радиусы и за раз получить трехмерное пространство Хафа (я так делать не пытался).
С прозрачностью есть такой нюанс, что если использовать 8 битный цвет и достаточно большое количество слоев, то BlendFactor будет меньше 10, вплоть до 1. Это может привести к большим погрешностям округления, и ступенчатому изменению яркости, если регулировать общую яркость с помощью BlendFactor. Однако, если яркость не регулировать, то сложно будет подобрать пороговое значение для фильтрации все из-за тех же погрешностей округления. Также, если использовать изображение с оттенками серого, оттенки пострадают, и даже буду потеряны при BlendFactor=1.
Эту проблему можно решить, используя большую глубину цвета для render target (например, 16 или 32 бита), если видеокарта это поддерживает.
Вот еще пример работы на зашумленном изображении. Исходное:

Результат (64 слоя):

Можно заметить, что алгоритм, скорее всего, опрашивает не все точки, составляющие окружность (если только окружность не слишком маленькая). С увеличением количества слоев, процент опрошенных точек и точность определения увеличивается, но возрастает время работы и появляются проблемы описанные выше.
Метод «прямых»
Анизотропная фильтрация
Прежде, чем перейти к описанию самого метода, нужно сделать отступление и рассказать подробнее об анизотропной фильтрации в видеокартах. При накладывании текстуры может случиться, что цвет одного экранного пикселя должны определять несколько точек текстуры (текселей). Это обычно случается либо при большом отдалении полигона от зрителя, либо при сильном наклоне полигона (хороший пример – текстура дороги). И если в первом случае можно заранее отмасштабировать текстуру на несколько разрешений, и потом брать нужный вариант (мип-маппинг), то во втором так сделать не получится так как текстура может оказаться повернута «в сторону зрителя» любой своей стороной.
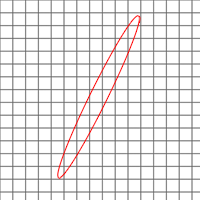
И тут видеокарты применяют всяческие ухищрения, но самый честный путь – взять все тексели из проекции пикселя на текстуру и посчитать их среднее значение. Это называется анизотропной (зависящей от направления) фильтрацией.
Максимальный традиционно поддерживаемый уровень анизотропной фильтрации – 16 (видимо, текселей).
О самом методе
Возьмем наше изображение и «сплющим» его, например, по вертикали. Т.е. отрендерим его целиком на прямоугольнике высотой в 1 пиксель. В идеале, вертикальные прямые превратятся в точки (максимумы). Все остальное размажется. Таким образом, значение одного параметра мы уже получили – это расстояние от левого края изображения до точки (до прямой на исходном изображении).
Теперь возьмем свежий экземпляр изображения, но перед сплющиванием повернем его на некоторый небольшой угол вокруг центра изображения по часовой стрелке. Потом сплющим. Некоторые прямые перейдут в точки. Это будут те прямые, которые наклонены на тот самый угол поворота изображения.
Таким образом, перебрав все углы от 0 до Пи, мы получим значения второго параметра – угла поворота картинки. По этим двум параметрам можно восстановить любую исходную прямую.
Остался только вопрос, как же грамотно сплющить изображение. Если сделать это в лоб – останется только шум – анизотропная фильтрация сработает, но возьмет лишь 16 текселей (пикселей исходной картинки). Это, скорее всего, слишком мало.
Можно порезать изображение на прямоугольники по 16 пикселей шириной, сплющить каждый отдельно,
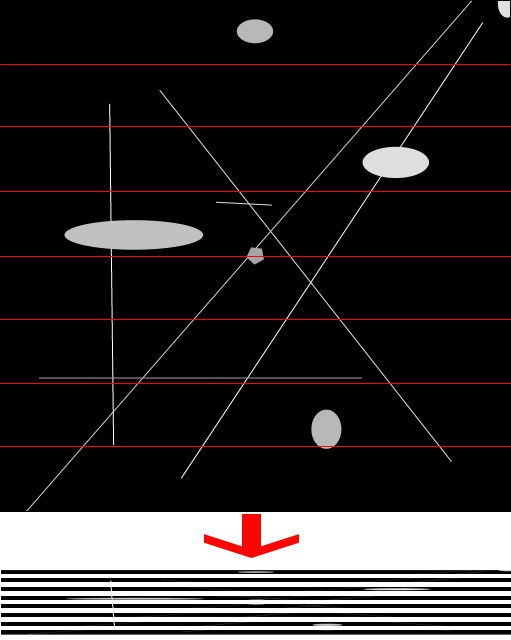
а потом отрисовать их поверх друг друга, как мы это делали в методе с окружностями. Вот это сработает, причем в результате будет учтен каждый пиксел.

(Можно считать, что картинки увеличены в 4 раза, чтоб было видно детали)
Если изображение выше, чем 16*256=4096 пикселей, можно нарезать его на прямоугольники большей высоты, либо использовать большую глубину цвета. Но, скорее всего, такое изображение просто не влезет в текстуру.
Для того, чтобы не потерять линии, находящиеся в углах, либо возле коротких сторон неквадратного изображения нужно брать render target шириной равной диагонали исходного изображения.
Код, настраивающий семплер текстур (поворот я делаю поворотом текстурных координат, поэтому нужно, чтобы семплер возвращал черный цвет, если текстуры где-то просто нет из-за поворота).
device.SamplerState[0].MinFilter = TextureFilter.Anisotropic;
device.SamplerState[0].MaxAnisotropy = 16;
device.SamplerState[0].AddressU = TextureAddress.Border;
device.SamplerState[0].AddressV = TextureAddress.Border;
device.SamplerState[0].AddressW = TextureAddress.Border;
device.SamplerState[0].BorderColor = Color.Black;
Создание прямоугольников
double sourceRectPixelWidth = sourceSize / n;
double targetRectPixelWidth = Math.Ceiling(sourceRectPixelWidth / anizotropy);
int angleValues = (int)Math.Floor(targetSize / targetRectPixelWidth);
float sourceRectWidth = (float)(sourceRectPixelWidth / sourceSize);
float tarectRectWidth = (float)(targetRectPixelWidth / targetSize);
for (int angleNumber = 0; angleNumber < angleValues; angleNumber++)
{
double angle = Math.PI / angleValues * angleNumber;
float targetShift = tarectRectWidth * angleNumber;
for (int sliceNumber = 0; sliceNumber < n; sliceNumber++)
{
float sourceShift = sourceRectWidth * sliceNumber;
rectangles.Add(new TexturedRect(
new Vector2(tarectRectWidth, 1f),
new Vector2(targetShift, 0f),
new Vector2(sourceRectWidth, 1f),
new Vector2(sourceShift, 0f),
(float)angle));
}
}
То же зашумленное изображение, что и в прошлом разделе, но теперь ищем линии (32 слоя, 512 шагов угла поворота):

Расширение метода «окружностей»
Изображения можно смещать не по радиусам окружностей, а более прихотливым способом. Например, выбираем некий произвольный искомый контур (даже не выражаемый с помощью формулы) и некую точку O.
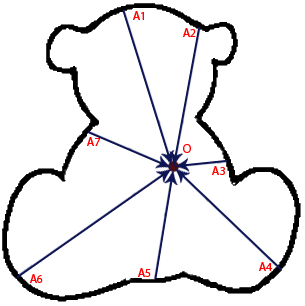
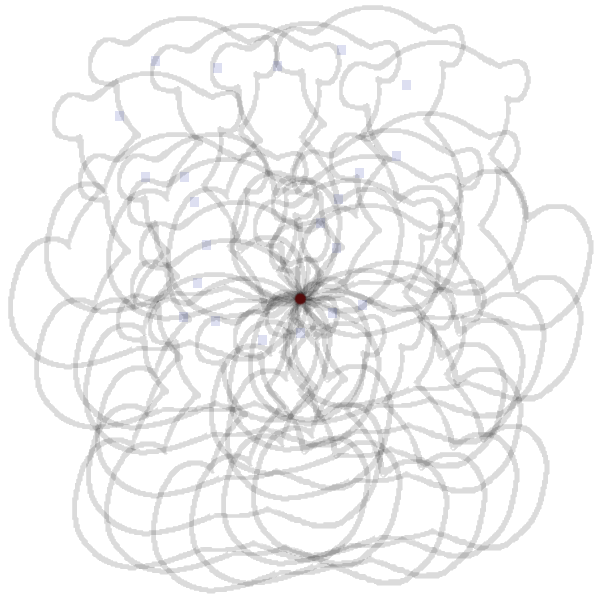
Затем, последовательно выбирая точки A1, A2 на контуре, смещаем слои изображения на вектора AO. Получается, что угол изображений описывает фигуру наподобие такой.

В этом случае будут найдены все мишки на изображении – максимумы придутся на точку, соответствующую точке O оригинального контура.
Дополнительные преимущества перед традиционным способом
- Экономия памяти (можно не копить все измерения в памяти)
- Можно не делать бинаризацию, а использовать оттенки серого. Это не повлияет на скорость работы и может увеличить точность
- Можно равномерно игнорировать часть точек в пользу скорости (В традиционном способе тоже можно так поступить, но придется прибегать к всяческим изощрениям, чтобы добиться равномерности, а не просто пропустить какой-нибудь угол)
- Можно работать с сильно зашумленными изображениями, это не уменьшит скорость
- Бонус. Можно использовать цветные изображения для получения красивых картинок наподобие той, что на КПДВ
Производительность
Будет не очень честно сравнивать производительность чистого подсчета между CPU и GPU, так как одна из тяжелых частей работы с GPU – это загрузка и выгрузка данных. Вряд ли стоит выгружать результаты работы в сыром виде обратно на CPU. Можно попробовать их сначала компактизовать, чтобы выгружать только найденные параметры фигур, а не точки. Однако, компактизация данных — тоже достаточно хитро реализуется на GPU, поэтому я даже не брался за нее пока.
Чисто производительность преобразования Хафа. Вход и выход – 2048*2048, GPU – GeForce GTS250:

Для сравнения результаты детектирования линий с помощью OpenCV. Вход – 2048*2048, выход 2048 шагов расстояния между линиями, CPU — Core i5 750 @ 3700Mhz.

Из этого времени 50-80 ms уходит на детектор границ Канни (после чего обрабатывается уже двуцветное изображение).
Вывод: в детектировании прямых на изображениях с малым количеством деталей GPU быстрее в 5-20 раз. На зашумленных/детализированных изображениях прирост скорости может составлять 100 – 300 раз.
Сравнить скорость детектирования окружностей не получилось, так как OpenCV использует не обычный, а градиентный метод Хафа.
Материалы по теме
Исходники проекта (Чтобы собрать нужен DirectX SDK June 2010)
Преобразование Хафа
Алгоритм Хафа для обнаружения произвольных кривых на изображениях
Hough Transform on GPU
Градиентный метод Хафа в OpenCV
UPD: Да, для того, чтобы запустить приложенный пример нужен .NET и DirectX, но сам принцип к ним не привязан. С тем же успехом можно реализовать его на c++ и OpenGL. CUDA и OpenCL все так же не понадобятся.