Доброго времени суток.
Сегодня я хочу коснуться темы сжатия данных без потерь. Несмотря на то, что на хабре уже были статьи, посвященные некоторым алгоритмам, мне захотелось рассказать об этом чуть более подробно.
Я постараюсь давать как математическое описание, так и описание в обычном виде, для того, чтобы каждый мог найти для себя что-то интересное.
В этой статье я коснусь фундаментальных моментов сжатия и основных типов алгоритмов.
Разумеется, да. Конечно, все мы понимаем, что сейчас нам доступны и носители информации большого объема, и высокоскоростные каналы передачи данных. Однако, одновременно с этим растут и объемы передаваемой информации. Если несколько лет назад мы смотрели 700-мегабайтные фильмы, умещающиеся на одну болванку, то сегодня фильмы в HD-качестве могут занимать десятки гигабайт.
Конечно, пользы от сжатия всего и вся не так много. Но все же существуют ситуации, в которых сжатие крайне полезно, если не необходимо.
Конечно, можно придумать еще множество различных ситуаций, в которых сжатие окажется полезным, но нам достаточно и этих нескольких примеров.
Все методы сжатия можно разделить на две большие группы: сжатие с потерями и сжатие без потерь. Сжатие без потерь применяется в тех случаях, когда информацию нужно восстановить с точностью до бита. Такой подход является единственно возможным при сжатии, например, текстовых данных.
В некоторых случаях, однако, не требуется точного восстановления информации и допускается использовать алгоритмы, реализующие сжатие с потерями, которое, в отличие от сжатия без потерь, обычно проще реализуется и обеспечивает более высокую степень архивации.
Итак, перейдем к рассмотрению алгоритмов сжатия без потерь.
В общем случае можно выделить три базовых варианта, на которых строятся алгоритмы сжатия.
Первая группа методов – преобразование потока. Это предполагает описание новых поступающих несжатых данных через уже обработанные. При этом не вычисляется никаких вероятностей, кодирование символов осуществляется только на основе тех данных, которые уже были обработаны, как например в LZ – методах (названных по имени Абрахама Лемпеля и Якоба Зива). В этом случае, второе и дальнейшие вхождения некой подстроки, уже известной кодировщику, заменяются ссылками на ее первое вхождение.
Вторая группа методов – это статистические методы сжатия. В свою очередь, эти методы делятся на адаптивные (или поточные), и блочные.
В первом (адаптивном) варианте, вычисление вероятностей для новых данных происходит по данным, уже обработанным при кодировании. К этим методам относятся адаптивные варианты алгоритмов Хаффмана и Шеннона-Фано.
Во втором (блочном) случае, статистика каждого блока данных высчитывается отдельно, и добавляется к самому сжатому блоку. Сюда можно отнести статические варианты методов Хаффмана, Шеннона-Фано, и арифметического кодирования.
Третья группа методов – это так называемые методы преобразования блока. Входящие данные разбиваются на блоки, которые затем трансформируются целиком. При этом некоторые методы, особенно основанные на перестановке блоков, могут не приводить к существенному (или вообще какому-либо) уменьшению объема данных. Однако после подобной обработки, структура данных значительно улучшается, и последующее сжатие другими алгоритмами проходит более успешно и быстро.
Все методы сжатия данных основаны на простом логическом принципе. Если представить, что наиболее часто встречающиеся элементы закодированы более короткими кодами, а реже встречающиеся – более длинными, то для хранения всех данных потребуется меньше места, чем если бы все элементы представлялись кодами одинаковой длины.
Точная взаимосвязь между частотами появления элементов, и оптимальными длинами кодов описана в так называемой теореме Шеннона о источнике шифрования(Shannon's source coding theorem), которая определяет предел максимального сжатия без потерь и энтропию Шеннона.
Если вероятность появления элемента si равна p(si), то наиболее выгодно будет представить этот элемент — log2p(si) битами. Если при кодировании удается добиться того, что длина всех элементов будет приведена к log2p(si) битам, то и длина всей кодируемой последовательности будет минимальной для всех возможных методов кодирования. При этом, если распределение вероятностей всех элементов F = {p(si)} неизменно, и вероятности элементов взаимно независимы, то средняя длина кодов может быть рассчитана как

Это значение называют энтропией распределения вероятностей F, или энтропией источника в заданный момент времени.
Однако обычно вероятность появления элемента не может быть независимой, напротив, она находится в зависимости от каких-то факторов. В этом случае, для каждого нового кодируемого элемента si распределение вероятностей F примет некоторое значение Fk, то есть для каждого элемента F= Fk и H= Hk.
Иными словами, можно сказать, что источник находится в состоянии k, которому соответствует некий набор вероятностей pk(si) для всех элементов si.
Поэтому, учитывая эту поправку, можно выразить среднюю длину кодов как
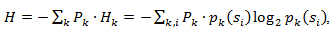
Где Pk — вероятность нахождения источника в состоянии k.
Итак, на данном этапе мы знаем, что сжатие основано на замене часто встречающихся элементов короткими кодами, и наоборот, а так же знаем, как определить среднюю длину кодов. Но что же такое код, кодирование, и как оно происходит?
Коды без памяти являются простейшими кодами, на основе которых может быть осуществлено сжатие данных. В коде без памяти каждый символ в кодируемом векторе данных заменяется кодовым словом из префиксного множества двоичных последовательностей или слов.
На мой взгляд, не самое понятное определение. Рассмотрим эту тему чуть более подробно.
Пусть задан некоторый алфавит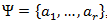 , состоящий из некоторого (конечного) числа букв. Назовем каждую конечную последовательность символов из этого алфавита (A=a1, a2,… ,an) словом, а число n — длиной этого слова.
, состоящий из некоторого (конечного) числа букв. Назовем каждую конечную последовательность символов из этого алфавита (A=a1, a2,… ,an) словом, а число n — длиной этого слова.
Пусть задан также другой алфавит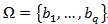 . Аналогично, обозначим слово в этом алфавите как B.
. Аналогично, обозначим слово в этом алфавите как B.
Введем еще два обозначения для множества всех непустых слов в алфавите. Пусть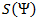 — количество непустых слов в первом алфавите, а
— количество непустых слов в первом алфавите, а 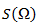 — во втором.
— во втором.
Пусть также задано отображение F, которое ставит в соответствие каждому слову A из первого алфавита некоторое слово B=F(A) из второго. Тогда слово B будет называться кодом слова A, а переход от исходного слова к его коду будет называться кодированием.
Поскольку слово может состоять и из одной буквы, то мы можем выявить соответствие букв первого алфавита и соответствующих им слов из второго:
a1 <-> B1
a2 <-> B2
…
an <-> Bn
Это соответствие называют схемой, и обозначают ∑.
В этом случае слова B1, B2,…, Bn называют элементарными кодами, а вид кодирования с их помощью — алфавитным кодированием. Конечно, большинство из нас сталкивались с таким видом кодирования, пусть даже и не зная всего того, что я описал выше.
Итак, мы определились с понятиями алфавит, слово, код, и кодирование. Теперь введем понятие префикс.
Пусть слово B имеет вид B=B'B''. Тогда B' называют началом, или префиксом слова B, а B'' — его концом. Это довольно простое определение, но нужно отметить, что для любого слова B, и некое пустое слово ʌ («пробел»), и само слово B, могут считаться и началами и концами.
Итак, мы подошли вплотную к пониманию определения кодов без памяти. Последнее определение, которое нам осталось понять — это префиксное множество. Схема ∑ обладает свойством префикса, если для любых 1≤i, j≤r, i≠j, слово Bi не является префиксом слова Bj.
Проще говоря, префиксное множество – это такое конечное множество, в котором ни один элемент не является префиксом (или началом) любого другого элемента. Простым примером такого множества является, например, обычный алфавит.
Итак, мы разобрались с основными определениями. Так как же происходит само кодирование без памяти?
Оно происходит в три этапа.
Одним из канонических алгоритмов, которые иллюстрируют данный метод, является алгоритм Хаффмана.
Алгоритм Хаффмана использует частоту появления одинаковых байт во входном блоке данных, и ставит в соответствие часто встречающимся блокам цепочки бит меньшей длины, и наоборот. Этот код является минимально – избыточным кодом. Рассмотрим случай, когда, не зависимо от входного потока, алфавит выходного потока состоит из всего 2 символов – нуля и единицы.
В первую очередь при кодировании алгоритмом Хаффмана, нам нужно построить схему ∑. Делается это следующим образом:
Шаги 2 и 3 повторяются до тех пор, пока в алфавите не останется только 1 псевдосимвол, содержащий все изначальные символы алфавита. При этом, поскольку на каждом шаге и для каждого символа происходит изменение соответствующего ему слова Bi (путем добавление единицы или нуля), то после завершения этой процедуры каждому изначальному символу алфавита ai будет соответствовать некий код Bi.
Для лучшей иллюстрации, рассмотрим небольшой пример.
Пусть у нас есть алфавит, состоящий из всего четырех символов — { a1, a2, a3, a4}. Предположим также, что вероятности появления этих символов равны соответственно p1=0.5; p2=0.24; p3=0.15; p4=0.11 (сумма всех вероятностей, очевидно, равна единице).
Итак, построим схему для данного алфавита.
Если сделать иллюстрацию этого процесса, получится примерно следующее:
Как вы видите, при каждом объединении мы присваиваем объединяемым символам коды 0 и 1.
Таким образом, когда дерево построено, мы можем легко получить код для каждого символа. В нашем случае коды будут выглядить так:
a1 = 0
a2 = 11
a3 = 100
a4 = 101
Поскольку ни один из данных кодов не является префиксом какого-нибудь другого (то есть, мы получили пресловутое префиксное множество), мы можем однозначно определить каждый код в выходном потоке.
Итак, мы добились того, что самый частый символ кодируется самым коротким кодом, и наоборот.
Если предположить, что изначально для хранения каждого символа использовался один байт, то можно посчитать, насколько нам удалось уменьшить данные.
Пусть на входу у нас была строка из 1000 символов, в которой символ a1 встречался 500 раз, a2 — 240, a3 — 150, и a4 — 110 раз.
Изначально данная строка занимала 8000 бит. После кодирования мы получим строку длинной в ∑pili = 500 * 1 + 240 * 2 + 150 * 3 + 110 * 3 = 1760 бит. Итак, нам удалось сжать данные в 4,54 раза, потратив в среднем 1,76 бита на кодирование каждого символа потока.
Напомню, что согласно Шеннону, средняя длина кодов составляет . Подставив в это уравнение наши значения вероятностей, мы получим среднюю длину кодов равную 1.75496602732291, что весьма и весьма близко к полученному нами результату.
. Подставив в это уравнение наши значения вероятностей, мы получим среднюю длину кодов равную 1.75496602732291, что весьма и весьма близко к полученному нами результату.
Тем не менее, следует учитывать, что помимо самих данных нам необходимо хранить таблицу кодировки, что слегка увеличит итоговый размер закодированных данных. Очевидно, что в разных случаях могут с использоваться разные вариации алгоритма – к примеру, иногда эффективнее использовать заранее заданную таблицу вероятностей, а иногда – необходимо составить ее динамически, путем прохода по сжимаемым данным.
Итак, в этой статье я постарался рассказать об общих принципах, по которым происходит сжатие без потерь, а также рассмотрел один из канонических алгоритмов — кодирование по Хаффману.
Если статья придется по вкусу хабросообществу, то я с удовольствием напишу продолжение, так как есть еще множество интересных вещей, касающихся сжатия без потерь; это как классические алгоритмы, так и предварительные преобразования данных (например, преобразование Барроуза-Уилира), ну и, конечно, специфические алгоритмы для сжатия звука, видео и изображений (самая, на мой взгляд, интересная тема).
Сегодня я хочу коснуться темы сжатия данных без потерь. Несмотря на то, что на хабре уже были статьи, посвященные некоторым алгоритмам, мне захотелось рассказать об этом чуть более подробно.
Я постараюсь давать как математическое описание, так и описание в обычном виде, для того, чтобы каждый мог найти для себя что-то интересное.
В этой статье я коснусь фундаментальных моментов сжатия и основных типов алгоритмов.
Сжатие. Нужно ли оно в наше время?
Разумеется, да. Конечно, все мы понимаем, что сейчас нам доступны и носители информации большого объема, и высокоскоростные каналы передачи данных. Однако, одновременно с этим растут и объемы передаваемой информации. Если несколько лет назад мы смотрели 700-мегабайтные фильмы, умещающиеся на одну болванку, то сегодня фильмы в HD-качестве могут занимать десятки гигабайт.
Конечно, пользы от сжатия всего и вся не так много. Но все же существуют ситуации, в которых сжатие крайне полезно, если не необходимо.
- Пересылка документов по электронной почте (особенно больших объемов документов с использованием мобильных устройств)
- При публикации документов на сайтах, потребность в экономии трафика
- Экономия дискового пространства в тех случаях, когда замена или добавление средств хранения затруднительно. Например, подобное бывает в тех случаях, когда выбить бюджет под капитальные расходы непросто, а дискового пространства не хватает
Конечно, можно придумать еще множество различных ситуаций, в которых сжатие окажется полезным, но нам достаточно и этих нескольких примеров.
Все методы сжатия можно разделить на две большие группы: сжатие с потерями и сжатие без потерь. Сжатие без потерь применяется в тех случаях, когда информацию нужно восстановить с точностью до бита. Такой подход является единственно возможным при сжатии, например, текстовых данных.
В некоторых случаях, однако, не требуется точного восстановления информации и допускается использовать алгоритмы, реализующие сжатие с потерями, которое, в отличие от сжатия без потерь, обычно проще реализуется и обеспечивает более высокую степень архивации.
| Сжатие с потерями |
| Лучшие степени сжатия, при сохранении «достаточно хорошего» качества данных. Применяются в основном для сжатия аналоговых данных — звука, изображений. В таких случаях распакованный файл может очень сильно отличаться от оригинала на уровне сравнения «бит в бит», но практически неотличим для человеческого уха или глаза в большинстве практических применений. |
| Сжатие без потерь |
| Данные восстанавливаются с точностью до бита, что не приводит к каким-либо потерям информации. Однако, сжатие без потерь показывает обычно худшие степени сжатия. |
Итак, перейдем к рассмотрению алгоритмов сжатия без потерь.
Универсальные методы сжатия без потерь
В общем случае можно выделить три базовых варианта, на которых строятся алгоритмы сжатия.
Первая группа методов – преобразование потока. Это предполагает описание новых поступающих несжатых данных через уже обработанные. При этом не вычисляется никаких вероятностей, кодирование символов осуществляется только на основе тех данных, которые уже были обработаны, как например в LZ – методах (названных по имени Абрахама Лемпеля и Якоба Зива). В этом случае, второе и дальнейшие вхождения некой подстроки, уже известной кодировщику, заменяются ссылками на ее первое вхождение.
Вторая группа методов – это статистические методы сжатия. В свою очередь, эти методы делятся на адаптивные (или поточные), и блочные.
В первом (адаптивном) варианте, вычисление вероятностей для новых данных происходит по данным, уже обработанным при кодировании. К этим методам относятся адаптивные варианты алгоритмов Хаффмана и Шеннона-Фано.
Во втором (блочном) случае, статистика каждого блока данных высчитывается отдельно, и добавляется к самому сжатому блоку. Сюда можно отнести статические варианты методов Хаффмана, Шеннона-Фано, и арифметического кодирования.
Третья группа методов – это так называемые методы преобразования блока. Входящие данные разбиваются на блоки, которые затем трансформируются целиком. При этом некоторые методы, особенно основанные на перестановке блоков, могут не приводить к существенному (или вообще какому-либо) уменьшению объема данных. Однако после подобной обработки, структура данных значительно улучшается, и последующее сжатие другими алгоритмами проходит более успешно и быстро.
Общие принципы, на которых основано сжатие данных
Все методы сжатия данных основаны на простом логическом принципе. Если представить, что наиболее часто встречающиеся элементы закодированы более короткими кодами, а реже встречающиеся – более длинными, то для хранения всех данных потребуется меньше места, чем если бы все элементы представлялись кодами одинаковой длины.
Точная взаимосвязь между частотами появления элементов, и оптимальными длинами кодов описана в так называемой теореме Шеннона о источнике шифрования(Shannon's source coding theorem), которая определяет предел максимального сжатия без потерь и энтропию Шеннона.
Немного математики
Если вероятность появления элемента si равна p(si), то наиболее выгодно будет представить этот элемент — log2p(si) битами. Если при кодировании удается добиться того, что длина всех элементов будет приведена к log2p(si) битам, то и длина всей кодируемой последовательности будет минимальной для всех возможных методов кодирования. При этом, если распределение вероятностей всех элементов F = {p(si)} неизменно, и вероятности элементов взаимно независимы, то средняя длина кодов может быть рассчитана как

Это значение называют энтропией распределения вероятностей F, или энтропией источника в заданный момент времени.
Однако обычно вероятность появления элемента не может быть независимой, напротив, она находится в зависимости от каких-то факторов. В этом случае, для каждого нового кодируемого элемента si распределение вероятностей F примет некоторое значение Fk, то есть для каждого элемента F= Fk и H= Hk.
Иными словами, можно сказать, что источник находится в состоянии k, которому соответствует некий набор вероятностей pk(si) для всех элементов si.
Поэтому, учитывая эту поправку, можно выразить среднюю длину кодов как
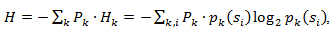
Где Pk — вероятность нахождения источника в состоянии k.
Итак, на данном этапе мы знаем, что сжатие основано на замене часто встречающихся элементов короткими кодами, и наоборот, а так же знаем, как определить среднюю длину кодов. Но что же такое код, кодирование, и как оно происходит?
Кодирование без памяти
Коды без памяти являются простейшими кодами, на основе которых может быть осуществлено сжатие данных. В коде без памяти каждый символ в кодируемом векторе данных заменяется кодовым словом из префиксного множества двоичных последовательностей или слов.
На мой взгляд, не самое понятное определение. Рассмотрим эту тему чуть более подробно.
Пусть задан некоторый алфавит
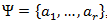 , состоящий из некоторого (конечного) числа букв. Назовем каждую конечную последовательность символов из этого алфавита (A=a1, a2,… ,an) словом, а число n — длиной этого слова.
, состоящий из некоторого (конечного) числа букв. Назовем каждую конечную последовательность символов из этого алфавита (A=a1, a2,… ,an) словом, а число n — длиной этого слова. Пусть задан также другой алфавит
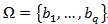 . Аналогично, обозначим слово в этом алфавите как B.
. Аналогично, обозначим слово в этом алфавите как B.Введем еще два обозначения для множества всех непустых слов в алфавите. Пусть
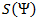 — количество непустых слов в первом алфавите, а
— количество непустых слов в первом алфавите, а 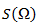 — во втором.
— во втором. Пусть также задано отображение F, которое ставит в соответствие каждому слову A из первого алфавита некоторое слово B=F(A) из второго. Тогда слово B будет называться кодом слова A, а переход от исходного слова к его коду будет называться кодированием.
Поскольку слово может состоять и из одной буквы, то мы можем выявить соответствие букв первого алфавита и соответствующих им слов из второго:
a1 <-> B1
a2 <-> B2
…
an <-> Bn
Это соответствие называют схемой, и обозначают ∑.
В этом случае слова B1, B2,…, Bn называют элементарными кодами, а вид кодирования с их помощью — алфавитным кодированием. Конечно, большинство из нас сталкивались с таким видом кодирования, пусть даже и не зная всего того, что я описал выше.
Итак, мы определились с понятиями алфавит, слово, код, и кодирование. Теперь введем понятие префикс.
Пусть слово B имеет вид B=B'B''. Тогда B' называют началом, или префиксом слова B, а B'' — его концом. Это довольно простое определение, но нужно отметить, что для любого слова B, и некое пустое слово ʌ («пробел»), и само слово B, могут считаться и началами и концами.
Итак, мы подошли вплотную к пониманию определения кодов без памяти. Последнее определение, которое нам осталось понять — это префиксное множество. Схема ∑ обладает свойством префикса, если для любых 1≤i, j≤r, i≠j, слово Bi не является префиксом слова Bj.
Проще говоря, префиксное множество – это такое конечное множество, в котором ни один элемент не является префиксом (или началом) любого другого элемента. Простым примером такого множества является, например, обычный алфавит.
Итак, мы разобрались с основными определениями. Так как же происходит само кодирование без памяти?
Оно происходит в три этапа.
- Составляется алфавит Ψ символов исходного сообщения, причем символы алфавита сортируются по убыванию их вероятности появления в сообщении.
- Каждому символу ai из алфавита Ψ ставится в соответствие некое слово Bi из префиксного множества Ω.
- Осуществляется кодирование каждого символа, с последующим объединением кодов в один поток данных, который будет являться результатам сжатия.
Одним из канонических алгоритмов, которые иллюстрируют данный метод, является алгоритм Хаффмана.
Алгоритм Хаффмана
Алгоритм Хаффмана использует частоту появления одинаковых байт во входном блоке данных, и ставит в соответствие часто встречающимся блокам цепочки бит меньшей длины, и наоборот. Этот код является минимально – избыточным кодом. Рассмотрим случай, когда, не зависимо от входного потока, алфавит выходного потока состоит из всего 2 символов – нуля и единицы.
В первую очередь при кодировании алгоритмом Хаффмана, нам нужно построить схему ∑. Делается это следующим образом:
- Все буквы входного алфавита упорядочиваются в порядке убывания вероятностей. Все слова из алфавита выходного потока (то есть то, чем мы будем кодировать) изначально считаются пустыми (напомню, что алфавит выходного потока состоит только из символов {0,1}).
- Два символа aj-1 и aj входного потока, имеющие наименьшие вероятности появления, объединяются в один «псевдосимвол» с вероятностью p равной сумме вероятностей входящих в него символов. Затем мы дописываем 0 в начало слова Bj-1, и 1 в начало слова Bj, которые будут впоследствии являться кодами символов aj-1 и aj соответственно.
- Удаляем эти символы из алфавита исходного сообщения, но добавляем в этот алфавит сформированный псевдосимвол (естественно, он должен быть вставлен в алфавит на нужное место, с учетом его вероятности).
Шаги 2 и 3 повторяются до тех пор, пока в алфавите не останется только 1 псевдосимвол, содержащий все изначальные символы алфавита. При этом, поскольку на каждом шаге и для каждого символа происходит изменение соответствующего ему слова Bi (путем добавление единицы или нуля), то после завершения этой процедуры каждому изначальному символу алфавита ai будет соответствовать некий код Bi.
Для лучшей иллюстрации, рассмотрим небольшой пример.
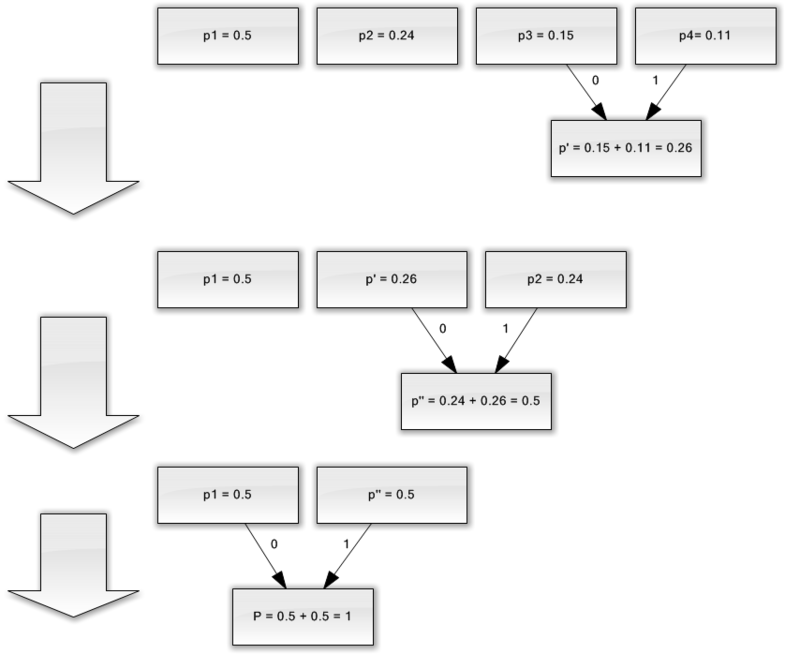
Пусть у нас есть алфавит, состоящий из всего четырех символов — { a1, a2, a3, a4}. Предположим также, что вероятности появления этих символов равны соответственно p1=0.5; p2=0.24; p3=0.15; p4=0.11 (сумма всех вероятностей, очевидно, равна единице).
Итак, построим схему для данного алфавита.
- Объединяем два символа с наименьшими вероятностями (0.11 и 0.15) в псевдосимвол p'.
- Удаляем объединенные символы, и вставляем получившийся псевдосимвол в алфавит.
- Объединяем два символа с наименьшей вероятностью (0.24 и 0.26) в псевдосимвол p''.
- Удаляем объединенные символы, и вставляем получившийся псевдосимвол в алфавит.
- Наконец, объединяем оставшиеся два символа, и получаем вершину дерева.
Если сделать иллюстрацию этого процесса, получится примерно следующее:

Как вы видите, при каждом объединении мы присваиваем объединяемым символам коды 0 и 1.
Таким образом, когда дерево построено, мы можем легко получить код для каждого символа. В нашем случае коды будут выглядить так:
a1 = 0
a2 = 11
a3 = 100
a4 = 101
Поскольку ни один из данных кодов не является префиксом какого-нибудь другого (то есть, мы получили пресловутое префиксное множество), мы можем однозначно определить каждый код в выходном потоке.
Итак, мы добились того, что самый частый символ кодируется самым коротким кодом, и наоборот.
Если предположить, что изначально для хранения каждого символа использовался один байт, то можно посчитать, насколько нам удалось уменьшить данные.
Пусть на входу у нас была строка из 1000 символов, в которой символ a1 встречался 500 раз, a2 — 240, a3 — 150, и a4 — 110 раз.
Изначально данная строка занимала 8000 бит. После кодирования мы получим строку длинной в ∑pili = 500 * 1 + 240 * 2 + 150 * 3 + 110 * 3 = 1760 бит. Итак, нам удалось сжать данные в 4,54 раза, потратив в среднем 1,76 бита на кодирование каждого символа потока.
Напомню, что согласно Шеннону, средняя длина кодов составляет
 . Подставив в это уравнение наши значения вероятностей, мы получим среднюю длину кодов равную 1.75496602732291, что весьма и весьма близко к полученному нами результату.
. Подставив в это уравнение наши значения вероятностей, мы получим среднюю длину кодов равную 1.75496602732291, что весьма и весьма близко к полученному нами результату. Тем не менее, следует учитывать, что помимо самих данных нам необходимо хранить таблицу кодировки, что слегка увеличит итоговый размер закодированных данных. Очевидно, что в разных случаях могут с использоваться разные вариации алгоритма – к примеру, иногда эффективнее использовать заранее заданную таблицу вероятностей, а иногда – необходимо составить ее динамически, путем прохода по сжимаемым данным.
Заключение
Итак, в этой статье я постарался рассказать об общих принципах, по которым происходит сжатие без потерь, а также рассмотрел один из канонических алгоритмов — кодирование по Хаффману.
Если статья придется по вкусу хабросообществу, то я с удовольствием напишу продолжение, так как есть еще множество интересных вещей, касающихся сжатия без потерь; это как классические алгоритмы, так и предварительные преобразования данных (например, преобразование Барроуза-Уилира), ну и, конечно, специфические алгоритмы для сжатия звука, видео и изображений (самая, на мой взгляд, интересная тема).
Литература
- Ватолин Д., Ратушняк А., Смирнов М. Юкин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео; ISBN 5-86404-170-X; 2003 г.
- Д. Сэломон. Сжатие данных, изображения и звука; ISBN 5-94836-027-Х; 2004г.
- www.wikipedia.org