Здравствуй, Хабр.
Большинство из нас так или иначе работает со строками. Этого не избежать — если ты пишешь код, ты обречен каждый день складывать строки, разбивать их на составные части и обращаться к отдельным символам по индексу. Мы давно привыкли что строки — это массивы символов фиксированной длины, а это влечет за собой соответствующие ограничения в работе с ними.
Так, мы не можем быстро объединить две строки — для этого нам потребуется сначала выделить необходимое количество памяти, а потом скопировать туда данные из конкатенируемых строк. Очевидно, что такая операция имеет сложность порядка О(n), где n — суммарная длина строк.
Именно поэтому код
работает так медленно.
Хочешь выполнять конкатенацию гигантских строк быстро? Не нравится, что строка требует для хранения непрерывную область памяти? Надоело использовать буферы для построения строк?
Структура данных, которая нас спасет, называется Rope string, или «веревочная строка». Принцип ее работы очень прост и до него можно догадаться буквально из интуитивных соображений.
Пусть нам требуется сложить две строки:
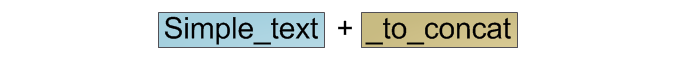
Для классических строк мы просто выделим область памяти необходимого размера, в начало её скопируем содержимое первой строки, а в конец — второй:
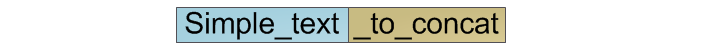
Как уже упоминалось выше, сложность этой операции — O(n).
Но что если мы используем информацию о том что наша результирующая строка — это конкатенация двух исходных? И действительно, создадим объект который предоставляет интерфейс строки и хранит в себе информацию о своих компонентах — исходных строках:

Такой способ объединения строк работает за О(1) — нам нужно лишь создать объект-обертку для исходных строк. Так как этот объект — тоже строка, его можно комбинировать с другими строками для получения нужных нам конкатенаций:
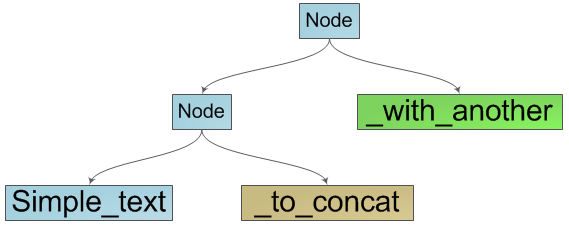
Уже сейчас очевидно что наша структура — это двоичное дерево поиска, в листьях которого находятся элементарные составляющие нашей строки — группы символов. Так же очевидным становится способ перечисления символов строки — это обход дерева в глубину с последовательным перечислением символов в листьях дерева.
Реализуем теперь операцию получения символа строки по его индексу. Для этого введем узлам дерева дополнительную характеристику — вес. Если в узле дерева хранится непосредственно часть символов (узел — лист) то его вес равен количеству этих символов. Иначе, вес узла равен сумме весов его потомков. Иными словами, вес узла — длина строки, которую он представляет.
Нам необходимо получить i-й символ строки, представленной узлом Node. Тогда могут возникнуть два случая:
Теперь мы умеем конкатенировать строки за О(1) и индексировать символы в них за О(h) — высоты дерева. Но для полного счастья необходимо научится быстро выполнять операции разбиения на две строки, удаления и вставки подстроки.
Итак, у нас есть строка и нам крайне необходимо разбить её на две подстроки в некоторой её позиции k (числа на схеме — размеры соответствующих деревьев):
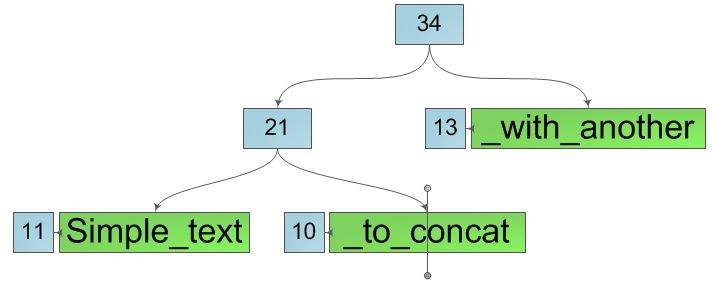
Место «разрыва» строки всегда находится в одном из листьев дерева. Разобьем этот лист на два новых, содержащих подстроки исходного листа. Причем для этой операции нам не понадобится копировать содержимое листа в новые, просто введем такие характеристики листа как offset и length и сохраним в новых листах указатели на массив символов исходного, изменив лишь смещение и длину:
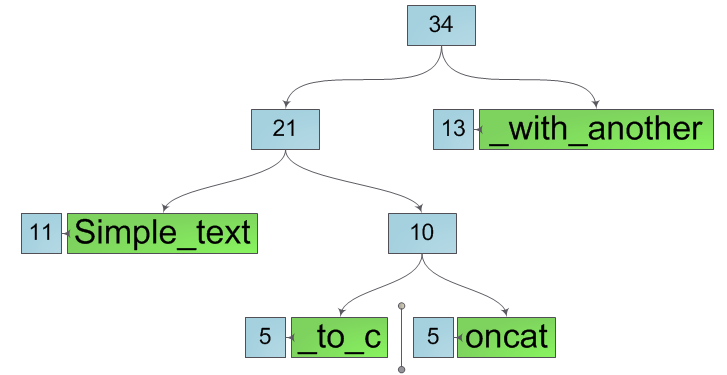
Далее будем расщеплять все узлы на пути от листа к корню, создавая вместо них пары узлов, принадлежащих, соответственно, левой и правой создаваемой подстроке. Причем мы опять же никак не изменяем текущий узел, а лишь создаем вместо него два новых. Это значит операция разделения строки порождает новые подстроки, не затрагивая исходную. После расщепления исходной строки мы получим две новые строки, как на рисунке ниже.
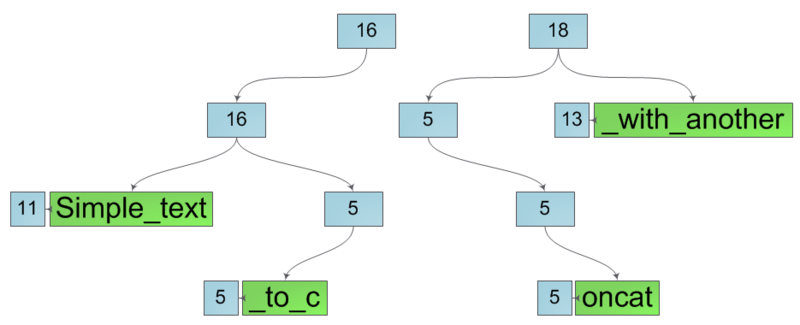
Нетрудно заметить что внутренняя структура таких строк не оптимальна — некоторые явно лишние. Однако исправить это досадное упущение легко — достаточно в обоих подстроках пройтись от места разреза к корню, заменяя каждый узел, имеющий ровно одного потомка этим самым потомком. После этого все лишние узлы пропадут и мы получим требуемые подстроки в их конечном виде:

Сложность же операции разбиения строк составляет, очевидно, О(h).
Благодаря реализованным уже операциям разбиения и слияния удаление и вставка делаются элементарно — для удаления подстроки достаточно разбить исходную строку в местах начала и окончания удаляемого участка и склеить крайние строки. Для вставки в строки в определенную позицию разобьем в ней исходную строку на две подстроки и склеим их со вставляемой в нужном порядке. Обе операции имеют асимптотику О(h).
Внимательный читатель, услышав слово «дерево» неизбежно вспомнил бы и два других — «логарифм» и «балансировка». И, как всегда, чтобы достичь заветной логарифмической асимптотики придется все таки балансировать наше дерево. Действительно, при нынешнем способе слияния строк внутренняя структура дерева будет похожа скорее на «лестницу», например такую, как на рисунке ниже:
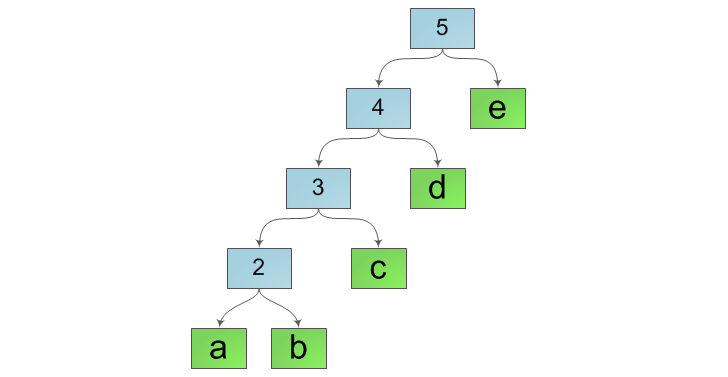
Чтобы этого избежать, будем при каждом объединении строк проверять сбалансированность результата и при необходимости пересобирать все дерево, балансируя его. Хорошее условие сбалансированности — длина строки должна быть не меньше (h+2) — го числа Фибоначчи. Обоснование этого условия а также пара дополнительных модификаций операции склейки были даны Боэмом, Аткинсоном и Плассом в их работе Ropes: an Alternative to Strings
Хранение в памяти узлов дерева вовсе не бесплатно. Если к строке прибавлять по одному символу то мы потратим на хранение информации об узлах дерева на порядок больше памяти, чем на сами символы строки. Во избежание таких ситуаций, а также для уменьшения высоты дерева целесообразно склеивать строки меньше некоторой длины (например, 32) «классическим» способом. Это сильно сэкономит память а также почти не отразится на производительности в целом.
В подавляющем числе случаев мы перебираем символы строки последовательно. В нашем случае, если мы запрашиваем символы по индексам i и i+1 очень велика вероятность того что физически они находятся в одном и том же листе дерева. Это значит что при поиске этих символов мы будем повторять один и тот же путь от корня дерева до листа. Очевидное решение этой проблемы — кэширование. Для этого при поиске очередного символа запомним лист в котором он находится и диапазон индексов, которые этот лист в себе содержит. После, при поиске очередного символа сперва будем проверять, лежит ли наш индекс в запомненном диапазоне и, если это так, будем искать его непосредственно в запомненном листе. Можно даже пойти дальше, запоминая не одну последнюю позицию а несколько, например, в циклическом списке.
Вкупе с предыдущей оптимизацией такая техника позволит нам улучшить асимптотику индексации с O(ln(n)) практически до О(1).
Что же мы в результате получим? Мы получим персистентную реализацию строки, не требующую для своего хранения непрерывной области памяти, с логарифмической асимптотикой вставки, удаления и конкатенации (вместо O(n) у классических строк) и индексацией почти за О(1) — вполне достойный внимания результат.
Ну и напоследок приведу пару полезных ссылок: статья в английской wiki, реализация на Java и описание С++ реализации на сайте SGI.
Use the ropes, Luke!
Большинство из нас так или иначе работает со строками. Этого не избежать — если ты пишешь код, ты обречен каждый день складывать строки, разбивать их на составные части и обращаться к отдельным символам по индексу. Мы давно привыкли что строки — это массивы символов фиксированной длины, а это влечет за собой соответствующие ограничения в работе с ними.
Так, мы не можем быстро объединить две строки — для этого нам потребуется сначала выделить необходимое количество памяти, а потом скопировать туда данные из конкатенируемых строк. Очевидно, что такая операция имеет сложность порядка О(n), где n — суммарная длина строк.
Именно поэтому код
string s = "";
for (int i = 0; i < 100000; i++) s += "a";работает так медленно.
Хочешь выполнять конкатенацию гигантских строк быстро? Не нравится, что строка требует для хранения непрерывную область памяти? Надоело использовать буферы для построения строк?
Структура данных, которая нас спасет, называется Rope string, или «веревочная строка». Принцип ее работы очень прост и до него можно догадаться буквально из интуитивных соображений.
Идея
Пусть нам требуется сложить две строки:
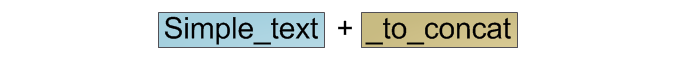
Для классических строк мы просто выделим область памяти необходимого размера, в начало её скопируем содержимое первой строки, а в конец — второй:
Как уже упоминалось выше, сложность этой операции — O(n).
Но что если мы используем информацию о том что наша результирующая строка — это конкатенация двух исходных? И действительно, создадим объект который предоставляет интерфейс строки и хранит в себе информацию о своих компонентах — исходных строках:

Такой способ объединения строк работает за О(1) — нам нужно лишь создать объект-обертку для исходных строк. Так как этот объект — тоже строка, его можно комбинировать с другими строками для получения нужных нам конкатенаций:

Уже сейчас очевидно что наша структура — это двоичное дерево поиска, в листьях которого находятся элементарные составляющие нашей строки — группы символов. Так же очевидным становится способ перечисления символов строки — это обход дерева в глубину с последовательным перечислением символов в листьях дерева.
Индексация
Реализуем теперь операцию получения символа строки по его индексу. Для этого введем узлам дерева дополнительную характеристику — вес. Если в узле дерева хранится непосредственно часть символов (узел — лист) то его вес равен количеству этих символов. Иначе, вес узла равен сумме весов его потомков. Иными словами, вес узла — длина строки, которую он представляет.
Нам необходимо получить i-й символ строки, представленной узлом Node. Тогда могут возникнуть два случая:
- Узел — лист. Тогда он содержит непосредственно данные и нам достаточно вернуть i-й символ «внутренней» строки.
- Узел — составной. Тогда необходимо узнать в каком потомке узла следует продолжить поиск. Если вес левого потомка больше i — искомый символ является i-м символом левой подстроки, иначе он является (i-w)-м символом правой подстроки, где w — вес левого поддерева.
Теперь мы умеем конкатенировать строки за О(1) и индексировать символы в них за О(h) — высоты дерева. Но для полного счастья необходимо научится быстро выполнять операции разбиения на две строки, удаления и вставки подстроки.
Разбиение
Итак, у нас есть строка и нам крайне необходимо разбить её на две подстроки в некоторой её позиции k (числа на схеме — размеры соответствующих деревьев):

Место «разрыва» строки всегда находится в одном из листьев дерева. Разобьем этот лист на два новых, содержащих подстроки исходного листа. Причем для этой операции нам не понадобится копировать содержимое листа в новые, просто введем такие характеристики листа как offset и length и сохраним в новых листах указатели на массив символов исходного, изменив лишь смещение и длину:

Далее будем расщеплять все узлы на пути от листа к корню, создавая вместо них пары узлов, принадлежащих, соответственно, левой и правой создаваемой подстроке. Причем мы опять же никак не изменяем текущий узел, а лишь создаем вместо него два новых. Это значит операция разделения строки порождает новые подстроки, не затрагивая исходную. После расщепления исходной строки мы получим две новые строки, как на рисунке ниже.

Нетрудно заметить что внутренняя структура таких строк не оптимальна — некоторые явно лишние. Однако исправить это досадное упущение легко — достаточно в обоих подстроках пройтись от места разреза к корню, заменяя каждый узел, имеющий ровно одного потомка этим самым потомком. После этого все лишние узлы пропадут и мы получим требуемые подстроки в их конечном виде:

Сложность же операции разбиения строк составляет, очевидно, О(h).
Удаление и вставка
Благодаря реализованным уже операциям разбиения и слияния удаление и вставка делаются элементарно — для удаления подстроки достаточно разбить исходную строку в местах начала и окончания удаляемого участка и склеить крайние строки. Для вставки в строки в определенную позицию разобьем в ней исходную строку на две подстроки и склеим их со вставляемой в нужном порядке. Обе операции имеют асимптотику О(h).
Оптимизация
Балансировка
Внимательный читатель, услышав слово «дерево» неизбежно вспомнил бы и два других — «логарифм» и «балансировка». И, как всегда, чтобы достичь заветной логарифмической асимптотики придется все таки балансировать наше дерево. Действительно, при нынешнем способе слияния строк внутренняя структура дерева будет похожа скорее на «лестницу», например такую, как на рисунке ниже:

Чтобы этого избежать, будем при каждом объединении строк проверять сбалансированность результата и при необходимости пересобирать все дерево, балансируя его. Хорошее условие сбалансированности — длина строки должна быть не меньше (h+2) — го числа Фибоначчи. Обоснование этого условия а также пара дополнительных модификаций операции склейки были даны Боэмом, Аткинсоном и Плассом в их работе Ropes: an Alternative to Strings
Прямое объединение малых строк
Хранение в памяти узлов дерева вовсе не бесплатно. Если к строке прибавлять по одному символу то мы потратим на хранение информации об узлах дерева на порядок больше памяти, чем на сами символы строки. Во избежание таких ситуаций, а также для уменьшения высоты дерева целесообразно склеивать строки меньше некоторой длины (например, 32) «классическим» способом. Это сильно сэкономит память а также почти не отразится на производительности в целом.
Кэширование последней позиции
В подавляющем числе случаев мы перебираем символы строки последовательно. В нашем случае, если мы запрашиваем символы по индексам i и i+1 очень велика вероятность того что физически они находятся в одном и том же листе дерева. Это значит что при поиске этих символов мы будем повторять один и тот же путь от корня дерева до листа. Очевидное решение этой проблемы — кэширование. Для этого при поиске очередного символа запомним лист в котором он находится и диапазон индексов, которые этот лист в себе содержит. После, при поиске очередного символа сперва будем проверять, лежит ли наш индекс в запомненном диапазоне и, если это так, будем искать его непосредственно в запомненном листе. Можно даже пойти дальше, запоминая не одну последнюю позицию а несколько, например, в циклическом списке.
Вкупе с предыдущей оптимизацией такая техника позволит нам улучшить асимптотику индексации с O(ln(n)) практически до О(1).
Итог
Что же мы в результате получим? Мы получим персистентную реализацию строки, не требующую для своего хранения непрерывной области памяти, с логарифмической асимптотикой вставки, удаления и конкатенации (вместо O(n) у классических строк) и индексацией почти за О(1) — вполне достойный внимания результат.
Ну и напоследок приведу пару полезных ссылок: статья в английской wiki, реализация на Java и описание С++ реализации на сайте SGI.
Use the ropes, Luke!