Задайтесь вопросом «ГДЕ?». Где находится центр управления движением галактик или поведением циклона? Где та сила, что объединяет атомы в сложные соединения, те в свою очередь — в цепочки белков, и порождает такие устойчивые и сложные явления как биологическая жизнь, разум, социум.
Под зонтиком теории сложности объединены разнообразные модели, которые описывают, как без центрального контроля из взаимодействия простых начальных элементов, подчиняющихся простым правилам, образуются явления более высокого порядка, обладающие сложно предсказуемым поведением и непредвиденными, но устойчивыми, свойствами.
Статья не предлагает готовых ответов о смысле жизни, сквозит грубыми нестрогими аналогиями, но при этом имеет дерзкую цель расширить кругозор читателя, опираясь на его воображение и некоторые математические факты.
Для начала давайте уясним, как сложное непредсказуемое поведение может возникать на основе простого детерминированного правила. Знакомьтесь, «Logistic Map»:
xn+1 = Rxn(1 — xn)
Спешу упредить возможную мысль «Ну вот скукота! Сейчас будут формулы…». Попытайтесь вникнуть, будет очень интересно.
Logistic Map – описывает итеративный процесс, в котором следующее значение функции аналитически детерминировано ее значением на предыдущем шаге. Построим графики этой функции для различных значений коэффициента “R”, приняв начальное значение X0 = 0.1
1) R = 2. График вырождается в линию:
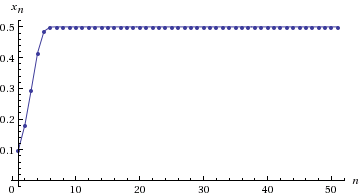
2) R = 3.1. Приходит к состоянию осцилляции между 2 значениями:
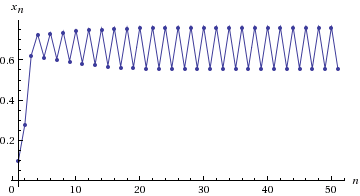
3) R = 3.47. Частота осцилляций 4:
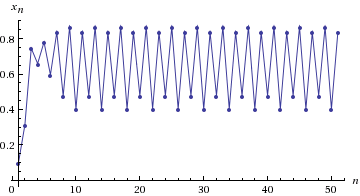
4) R = 3.55. Частота осцилляций 8:
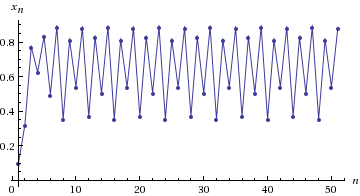
5) А теперь R = 3.999:
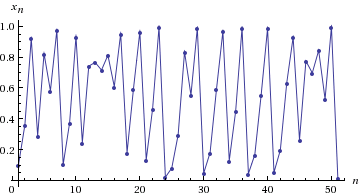
В этом графике нет регулярностей. При R = 3.999 мы наблюдаем хаос. Под хаосом понимают крайнюю чувствительность конечного результата по отношению к начальным данным. Давайте изменим начальное значение X0 = 0.1000000001 (единица в 10 знаке) и построим график красным цветом поверх предыдущего результата.

Эта картинка может служить иллюстрацией т.н. «эффекта бабочки». В результате незначительного изменения начального значения в 10 знаке после запятой уже на 30 итерации мы получаем совершенно другой график. Это свойство настолько примечательно, что его используют в генераторах псевдослучайных чисел.
Мы получим абсолютно разные графики, построив их для некоторого иррационального числа, вычисленного с разной (крайне незначительной) точностью. Не верьте мне на слово, берите (1 / sqrt(2)) и дерзайте!
Таким образом, мы узнали, что сложное хаотическое поведение, кажущееся случайным, может возникать в системах на основе простых детерминированных правил. Причем это поведение невозможно предсказать в долгосрочной перспективе из-за сильной чувствительности поведения к начальным условиям (или неточности физических измерений).
Посмотрим на еще один интересный пример – клеточные автоматы, и в частности, — игру Джона Конвэя «Жизнь».
Правила игры задают только поведение отдельной клетки среди ближайших соседей. Однако имеем, что в игровой клеточной среде без какого-либо изначального предписания возникают устойчивые явления более высокого порядка. Жизнь отдельных клеток, которые строго привязаны к своим позициям, порождает устойчивые возмущения в среде, называемые паттернами. Возмущения могут быть статичными, находится в состоянии осцилляции либо проявлять более сложное поведение. Например, двигаться и сталкиваться, коллапсируя или порождая новые образования с причудливыми свойствами.
Несколько картинок из википедии для поддержания интереса:
Такие свойства или явления, которые не были явно заданы изначально, но возникающие в результате процессов взаимодействия исходных составляющих, называются эмерджентными (дословно, возникающими). Эти свойства создаются и поддерживаются процессами внутри среды. Как только процессы исчезают – свойства также исчезают, как исчезает жизнь если разобрать организм на составляющие, а потом механически попытаться собрать воедино.
Эмерджентные свойства – неотъемлемая особенность сложных систем.
Нырнём глубже и обратимся к работе Стивена Вольфрама, опубликованной в книге «New Kind of Science».
Вольфрам провел эксперименты с самым простым вариантом игры жизнь, в котором среда представляет собой длинную замкнутую ленту шириной в одну клетку. Им двигала идея, что если нельзя понять, что происходит в этом самом простом клеточном автомате, то о более сложных системах и нечего думать.
Правила просты. Клетка может быть живой либо мертвой в зависимости от своего прежнего состояния и состояния двух её соседей. Итого, последующее состояние клетки определяется тремя параметрами.
А теперь потерпите — поупражняемся в комбинаторике…
Из возможных состояний 3 ячеек можно составить лишь 8 возможных комбинаций.
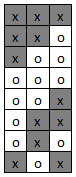
Каждая комбинация может переводить клетку в одно из 2 возможных состояний (вкл. и выкл.) Итого получается небольшое конечное число возможных правил: 256 (28).
На каждом правиле Вольфрам провел серию экспериментов с различными начальными данными и в результате выделил 4 класса правил:
1) Почти все начальные конфигурации устанавливаются в один и тот же финальный паттерн
2) Почти все начальные конфигурации устанавливаются в один и тот же финальный паттерн или циркулируют между несколькими финальными паттернами
3) Большинство начальных конфигураций создают выглядящее случайным поведение, а также порождают треугольники или другие регулярные структуры
4) Последний класс объединяет порядок и случайность, порождая локализованные структуры, которые будучи простыми сами по себе, двигаются и взаимодействуют друг с другом очень сложным образом.
Картинка для поддержания внимания:

Класс 4 является самым интересным. Примером правила 4 класса может служить «правило 110», иллюстрированное выше.
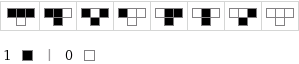
Есть кое-что неожиданное в нём. Ученик Вольфрама Мэтью Кук доказал, что… (барабанная дробь...) это правило является Тьюринг-полным. Иными словами – это простейшая известная на данный момент вычислительная модель.
Вольфрам высказал предположение, что некоторое подобное простое правило может лежать в основе всех законов природы. По его словам, мир представляет собой сложную систему, порожденную этим простым правилом на неком вселенском клеточном автомате от большого взрыва и до мгновения, когда вы читаете эти строки.
Это утверждение упирается в священные споры о том, является ли вселенная вычислимой или вычисление – это лишь ментальная модель, позволяющая нам описывать с некоторой точностью след от «чего-то происходящего как-то».
В статье описаны лишь несколько базовых моделей теории сложности. Эти формализмы позволяют объяснить, как из поведения простейших базовых элементов способны возникать сложные явления на уровне целой системы.
Я не коснулся моделей эволюции, адаптации, социальной самоорганизации, основанной на теории игр и теории сетей. Если статья найдет отклик – возможно, я напишу еще одну, где постараюсь осветить и эти аспекты.
Некоторые компании берут на вооружение самоорганизацию, как способ существования социальной организации. То есть, отказываясь от центрального контроля, они дают полную свободу индивиду выбирать, чем заниматься: примкнуть к готовой проектной группе или, начав свой проект, заниматься поиском и вдохновлением единомышленников. Можно найти аналогию с иммунной системой, атакующей вирусы – интересные задачи находят своих исполнителей. Пока вектор деятельности специалиста совпадает с вектором компании – всё идет впрок, иначе социальная система отторгнет инородное тело :)
Также некоторые модели теории сложности лежат в основе гибких методологий разработки, где в отличие от ватерфола, система не специфицируется полностью заранее, а гибко адаптируется к внешним требованиям.
Complexity. A guided tour
New Kind of Science
Complexity Theory for Software Developers
Видео: Стэнфордские лекции. Emergence and Complexity
Видео: Презентация NKS от Стивена Вольфрама
Видео: вселенная как клеточный автомат
Корпоративная культура в компании Valve
Под зонтиком теории сложности объединены разнообразные модели, которые описывают, как без центрального контроля из взаимодействия простых начальных элементов, подчиняющихся простым правилам, образуются явления более высокого порядка, обладающие сложно предсказуемым поведением и непредвиденными, но устойчивыми, свойствами.
Статья не предлагает готовых ответов о смысле жизни, сквозит грубыми нестрогими аналогиями, но при этом имеет дерзкую цель расширить кругозор читателя, опираясь на его воображение и некоторые математические факты.
Предсказуемая непредсказуемость
Для начала давайте уясним, как сложное непредсказуемое поведение может возникать на основе простого детерминированного правила. Знакомьтесь, «Logistic Map»:
xn+1 = Rxn(1 — xn)
Спешу упредить возможную мысль «Ну вот скукота! Сейчас будут формулы…». Попытайтесь вникнуть, будет очень интересно.
Logistic Map – описывает итеративный процесс, в котором следующее значение функции аналитически детерминировано ее значением на предыдущем шаге. Построим графики этой функции для различных значений коэффициента “R”, приняв начальное значение X0 = 0.1
1) R = 2. График вырождается в линию:

2) R = 3.1. Приходит к состоянию осцилляции между 2 значениями:

3) R = 3.47. Частота осцилляций 4:

4) R = 3.55. Частота осцилляций 8:

5) А теперь R = 3.999:

В этом графике нет регулярностей. При R = 3.999 мы наблюдаем хаос. Под хаосом понимают крайнюю чувствительность конечного результата по отношению к начальным данным. Давайте изменим начальное значение X0 = 0.1000000001 (единица в 10 знаке) и построим график красным цветом поверх предыдущего результата.

Эта картинка может служить иллюстрацией т.н. «эффекта бабочки». В результате незначительного изменения начального значения в 10 знаке после запятой уже на 30 итерации мы получаем совершенно другой график. Это свойство настолько примечательно, что его используют в генераторах псевдослучайных чисел.
Мы получим абсолютно разные графики, построив их для некоторого иррационального числа, вычисленного с разной (крайне незначительной) точностью. Не верьте мне на слово, берите (1 / sqrt(2)) и дерзайте!
Таким образом, мы узнали, что сложное хаотическое поведение, кажущееся случайным, может возникать в системах на основе простых детерминированных правил. Причем это поведение невозможно предсказать в долгосрочной перспективе из-за сильной чувствительности поведения к начальным условиям (или неточности физических измерений).
Игра «Жизнь»
Посмотрим на еще один интересный пример – клеточные автоматы, и в частности, — игру Джона Конвэя «Жизнь».
Правила игры задают только поведение отдельной клетки среди ближайших соседей. Однако имеем, что в игровой клеточной среде без какого-либо изначального предписания возникают устойчивые явления более высокого порядка. Жизнь отдельных клеток, которые строго привязаны к своим позициям, порождает устойчивые возмущения в среде, называемые паттернами. Возмущения могут быть статичными, находится в состоянии осцилляции либо проявлять более сложное поведение. Например, двигаться и сталкиваться, коллапсируя или порождая новые образования с причудливыми свойствами.
Несколько картинок из википедии для поддержания интереса:
 |
 |
 |
Такие свойства или явления, которые не были явно заданы изначально, но возникающие в результате процессов взаимодействия исходных составляющих, называются эмерджентными (дословно, возникающими). Эти свойства создаются и поддерживаются процессами внутри среды. Как только процессы исчезают – свойства также исчезают, как исчезает жизнь если разобрать организм на составляющие, а потом механически попытаться собрать воедино.
Эмерджентные свойства – неотъемлемая особенность сложных систем.
Клеточные автоматы Стивена Вольфрама и «правило 110»
Нырнём глубже и обратимся к работе Стивена Вольфрама, опубликованной в книге «New Kind of Science».
Вольфрам провел эксперименты с самым простым вариантом игры жизнь, в котором среда представляет собой длинную замкнутую ленту шириной в одну клетку. Им двигала идея, что если нельзя понять, что происходит в этом самом простом клеточном автомате, то о более сложных системах и нечего думать.
Правила просты. Клетка может быть живой либо мертвой в зависимости от своего прежнего состояния и состояния двух её соседей. Итого, последующее состояние клетки определяется тремя параметрами.
А теперь потерпите — поупражняемся в комбинаторике…
Из возможных состояний 3 ячеек можно составить лишь 8 возможных комбинаций.

Каждая комбинация может переводить клетку в одно из 2 возможных состояний (вкл. и выкл.) Итого получается небольшое конечное число возможных правил: 256 (28).
На каждом правиле Вольфрам провел серию экспериментов с различными начальными данными и в результате выделил 4 класса правил:
1) Почти все начальные конфигурации устанавливаются в один и тот же финальный паттерн
2) Почти все начальные конфигурации устанавливаются в один и тот же финальный паттерн или циркулируют между несколькими финальными паттернами
3) Большинство начальных конфигураций создают выглядящее случайным поведение, а также порождают треугольники или другие регулярные структуры
4) Последний класс объединяет порядок и случайность, порождая локализованные структуры, которые будучи простыми сами по себе, двигаются и взаимодействуют друг с другом очень сложным образом.
Картинка для поддержания внимания:

Класс 4 является самым интересным. Примером правила 4 класса может служить «правило 110», иллюстрированное выше.

Есть кое-что неожиданное в нём. Ученик Вольфрама Мэтью Кук доказал, что… (барабанная дробь...) это правило является Тьюринг-полным. Иными словами – это простейшая известная на данный момент вычислительная модель.
Вольфрам высказал предположение, что некоторое подобное простое правило может лежать в основе всех законов природы. По его словам, мир представляет собой сложную систему, порожденную этим простым правилом на неком вселенском клеточном автомате от большого взрыва и до мгновения, когда вы читаете эти строки.
Это утверждение упирается в священные споры о том, является ли вселенная вычислимой или вычисление – это лишь ментальная модель, позволяющая нам описывать с некоторой точностью след от «чего-то происходящего как-то».
Заключение
В статье описаны лишь несколько базовых моделей теории сложности. Эти формализмы позволяют объяснить, как из поведения простейших базовых элементов способны возникать сложные явления на уровне целой системы.
Я не коснулся моделей эволюции, адаптации, социальной самоорганизации, основанной на теории игр и теории сетей. Если статья найдет отклик – возможно, я напишу еще одну, где постараюсь осветить и эти аспекты.
Некоторые компании берут на вооружение самоорганизацию, как способ существования социальной организации. То есть, отказываясь от центрального контроля, они дают полную свободу индивиду выбирать, чем заниматься: примкнуть к готовой проектной группе или, начав свой проект, заниматься поиском и вдохновлением единомышленников. Можно найти аналогию с иммунной системой, атакующей вирусы – интересные задачи находят своих исполнителей. Пока вектор деятельности специалиста совпадает с вектором компании – всё идет впрок, иначе социальная система отторгнет инородное тело :)
Также некоторые модели теории сложности лежат в основе гибких методологий разработки, где в отличие от ватерфола, система не специфицируется полностью заранее, а гибко адаптируется к внешним требованиям.
Рекомендуемые источники
Complexity. A guided tour
New Kind of Science
Complexity Theory for Software Developers
Видео: Стэнфордские лекции. Emergence and Complexity
Видео: Презентация NKS от Стивена Вольфрама
Видео: вселенная как клеточный автомат
Корпоративная культура в компании Valve