За последнюю неделю Хабр пополнился сразу несколькими статьями об игре «Жизнь». Что ж, тогда и я поделюсь своими наработками по этой теме.
Минувшим летом мне довелось побывать на летней школе по параллельному программированию, проводимой НГУ. В рамках школы каждый студент должен был подготовить какой-либо проект по одной из тематик, озвученных на лекциях. Меня заинтересовали клеточные автоматы. У меня первая ассоциация при фразе «клеточный автомат» это именно «Жизнь».
Я понимал, что никому не будет интересно наблюдать за черными клеточками, живущими на экране. Да и слишком просто это для такого проекта. Нужно было придумать что-то принципиально новое. Я решил расширить диапазон своих мыслей и выйти за пределы двухмерного пространства. В прямом смысле. Я подумал, а почему бы не сделать эту игру трехмерной? Ведь это гораздо интереснее!
Думаю, здесь все (ну или почти все) представляют себе клеточный автомат. Поэтому мы не будем углубляться в теорию, а сразу перейдем к практике. Единственное, что отличает этот клеточный автомат от самого примитивного это то, что было необходимо распараллелить вычисления. В дальнейшем, правда, будет добавлено еще кое-что, но пока не будем об этом. Клеточный автомат (далее КА) для наших целей должен быть синхронным. К счастью, даже при параллельной реализации алгоритма это не создает никаких неудобств. При работе с OpenMP достаточно просто поместить цикл, вычисляющий значение КА в блок #pragma omp for {}.
Было бы не плохо, если бы все это можно было увидеть воочию. И мне повезло, потому что буквально за месяц до этого я мало-мало освоил работу с OpenGL с использованием библиотеки freeglut. Так же хотелось, чтобы игровое пространство можно было вращать, приближать и отдалять. Управление осуществляется при помощи мышки и клавиатуры. Мышь поворачивает, клавиатура двигает. Так же с клавиатуры происходит управление самой «Жизнью». Так как для восприятия трехмерного пространства требуется больше времени, чем для двухмерного, было решено переходить к очередному шагу по нажатию на клавишу.
Первые тесты визуализатора прошли на ура. Но при попытке подсунуть ему массив из 100*100*100 (или больше, точно не помню) клеток, каждый кадр отрисовывался вплоть до 8 секунд. Это не дело. Тут я вспомнил про пирамиду видимости. К сожалению, отрисовка по этой самой пирамиде занимала почти такое же время, так как большую часть времени пространство полностью было видно. При приближении к центру этого пространства и дельнейшем движении за него время отрисовки уменьшалось значительно.
Время еще оставалось, а проект уже был готов к сдаче. Я понял, что чего-то не хватает. А вот чего именно – вопрос посложнее. Через некоторое время раздумий я решил, что мой КА совсем не похож на настоящую жизнь. Не хватает внешних факторов, влияющих на размножение клеток. В качестве такого фактора была выбрана температура.
Если кратко, то есть некая температура, назовем ее оптимальной, при которой выживаемость и рождаемость максимальные. При уменьшении и увеличении температуры выжить становится труднее. Но просто задать температуру было бы не интересно. И снова прибегнем к КА. В начальном состоянии температура сконцентрирована в центре пространства. С течением времени «теплый воздух» равномерно распределяется по всему пространству. Достигается это диффузией. Да не простой, а целочисленной. В данном случае это заключается в том, что некоторая часть температуры в клетке остается, а остальной частью соседние клетки обмениваются. Такой клеточный автомат уже не может быть синхронным, так как было ты странным, если бы все клетки одновременно поменялись… А чтобы его можно было запрограммировать под несколько процессов, необходимо прибегнуть к хитрости – перейти от асинхронного КА к блочно-синхронному. Смысл в том, что каждому процессу выделяется некоторый блок. Внутри этого блока КА является асинхронным. Но между собой блоки синхронизируются. На картинке клетки одного цвета просчитываются в одно время.

Конечно, данная реализация не является идеальной. Код никак не оптимизирован. В первую очередь можно улучшить визуализатор. Помимо отсечения по пирамиде видимости добавить отсечение по Z-буферу, чтобы те клетки, которые скрыты клетками переднего плана, не рисовались.
Вообще, проект можно раздуть до космических масштабов. Например, хочется добавить дополнительные слои. Если говорить только о внешних воздействиях, то это может быть, например, рельеф. На больших высотах клетки будут находиться с меньшей вероятностью. К тому же, там будет холоднее. Можно добавить слой с растительностью, которая будет служить пищей. А можно клонировать слой с самими клетками и создать несколько видов организмов, которые будут друг друга поедать. Можно добавить мутации и многое-многое другое. Было бы желание.
Теперь, наконец, можно перейти к самому интересному.
Сначала программа тестировалась без температурного слоя, так как к тому времени его просто не было. К сожалению, программа не имеет нормального интерфейса, и мне пришлось написать генератор тестов. Он не представляет особого интереса. Единственная его задача – сделать в центре игрового пространства кубик из клеток. Ниже представлены кубики 3х3х3, 4х4х4 и 5х5х5. Здесь представлены только некоторые шаги, чтоб сложилась общая картина происходящего.
3х3х3, шаг 1:

3х3х3, шаг 4:
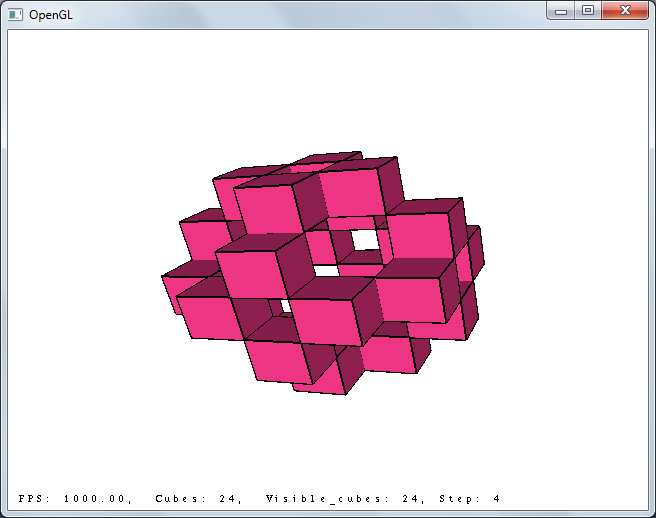
3х3х3, шаги 5 и 6:
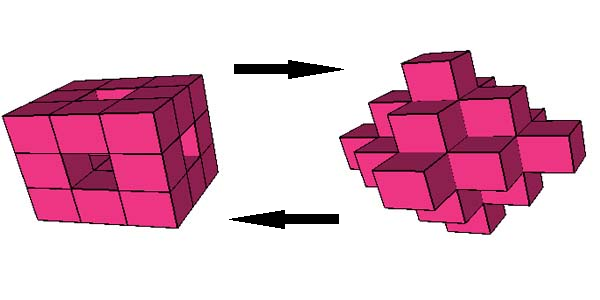
Получается довольно забавная мигалка.
4х4х4, шаг 1:
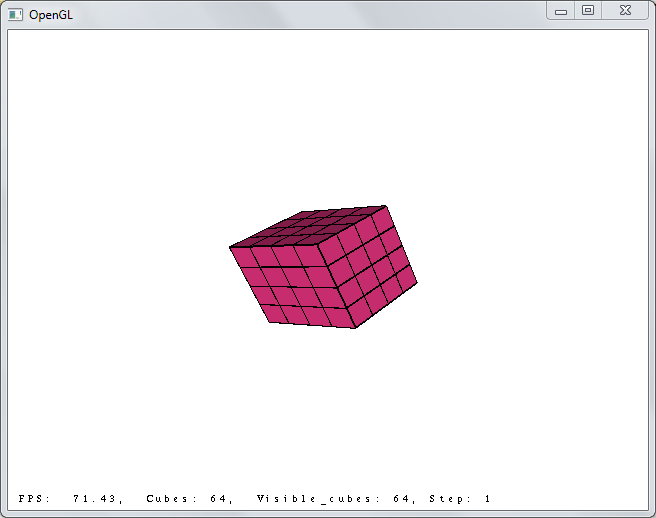
4х4х4, шаг 10:

4х4х4, шаг 100:
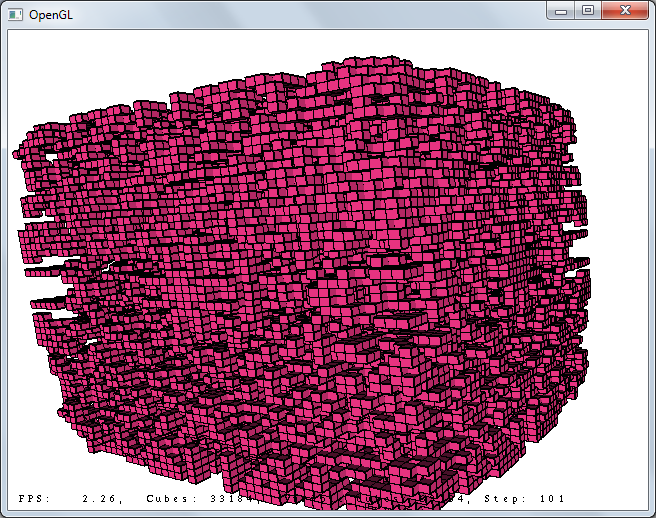
Дальше практически ничего не меняется.
5х5х5, шаг 1:
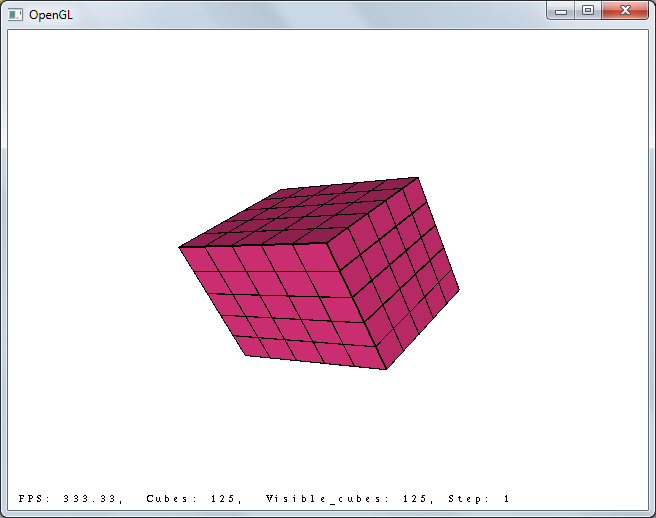
5х5х5, шаг 4:
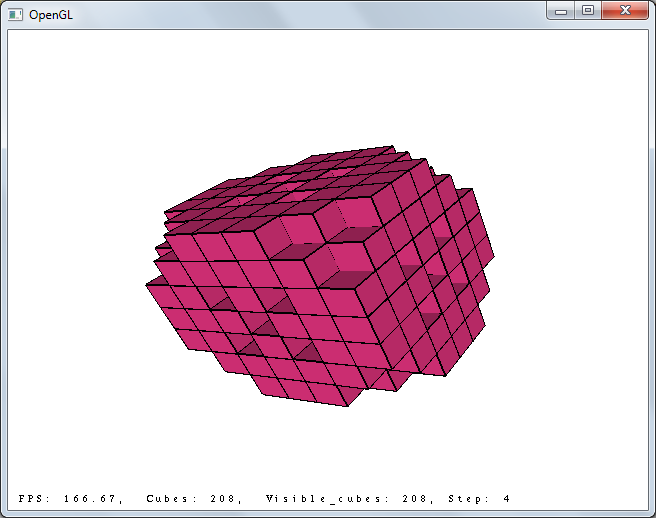
5х5х5, шаг 7:

5х5х5, шаг 8:

На следующем шаге не остается ни одной живой клетки.
Теперь к кубику 4х4х4 добавим температуру. Температурный слой представлен в виде центрального среза. Красный цвет – оптимальная температура, желтый – чуть ниже нормы, розовый – низкая. Игровое пространство имеет размеры 50х50х50, в центре расположен куб 40х40х40 с оптимальной температурой. Вот что получилось.
Шаг 1:

Шаг 10:

Шаг 50:

Шаг 150:

Шаг 200:

Все предельно ясно: воздух остывает, жизнь прекращается.
К сожалению, самой программой поделиться не могу, так как входные данные жестко задаются в генераторе. Зато могу поделиться исходниками, но предупреждаю сразу: код просто ужасен.
Предисловие
Минувшим летом мне довелось побывать на летней школе по параллельному программированию, проводимой НГУ. В рамках школы каждый студент должен был подготовить какой-либо проект по одной из тематик, озвученных на лекциях. Меня заинтересовали клеточные автоматы. У меня первая ассоциация при фразе «клеточный автомат» это именно «Жизнь».
Я понимал, что никому не будет интересно наблюдать за черными клеточками, живущими на экране. Да и слишком просто это для такого проекта. Нужно было придумать что-то принципиально новое. Я решил расширить диапазон своих мыслей и выйти за пределы двухмерного пространства. В прямом смысле. Я подумал, а почему бы не сделать эту игру трехмерной? Ведь это гораздо интереснее!
Этап 1. Клеточный автомат
Думаю, здесь все (ну или почти все) представляют себе клеточный автомат. Поэтому мы не будем углубляться в теорию, а сразу перейдем к практике. Единственное, что отличает этот клеточный автомат от самого примитивного это то, что было необходимо распараллелить вычисления. В дальнейшем, правда, будет добавлено еще кое-что, но пока не будем об этом. Клеточный автомат (далее КА) для наших целей должен быть синхронным. К счастью, даже при параллельной реализации алгоритма это не создает никаких неудобств. При работе с OpenMP достаточно просто поместить цикл, вычисляющий значение КА в блок #pragma omp for {}.
Примерно вот так
#pragma omp parallel shared(Temp, Space, Size) private(Num_of_nbr, x, y, z)
{
#pragma omp for
for (x = 0; x < Size; x++)
for (y = 0; y < Size; y++)
for (z = 0; z < Size; z++)
{
// Neighbors(x, y, z) вычисляет кол-во соседей
//у клетки с координатами x, y и z
Num_of_nbr = Neighbors(x, y, z);
if (Space[x][y][z] == 1)
if (Num_of_nbr <= Smid + Sdiff * Koeff[Int_Temp[x][y][z]] \
&& Num_of_nbr >= Smid - Sdiff * Koeff[Int_Temp[x][y][z]])
Temp[x][y][z] = 1;
else Temp[x][y][z] = 0;
else
if (Num_of_nbr <= Bmid + Bdiff * Koeff[Int_Temp[x][y][z]] \
&& Num_of_nbr >= Bmid - Bdiff * Koeff[Int_Temp[x][y][z]])
Temp[x][y][z] = 1;
else Temp[x][y][z] = 0;
}
#pragma omp for
for (x = 0; x < Size; x++)
for (y = 0; y < Size; y++)
for (z = 0; z < Size; z++)
Space[x][y][z] = Temp[x][y][z];
}
Этап 2. Визуализатор
Было бы не плохо, если бы все это можно было увидеть воочию. И мне повезло, потому что буквально за месяц до этого я мало-мало освоил работу с OpenGL с использованием библиотеки freeglut. Так же хотелось, чтобы игровое пространство можно было вращать, приближать и отдалять. Управление осуществляется при помощи мышки и клавиатуры. Мышь поворачивает, клавиатура двигает. Так же с клавиатуры происходит управление самой «Жизнью». Так как для восприятия трехмерного пространства требуется больше времени, чем для двухмерного, было решено переходить к очередному шагу по нажатию на клавишу.
Первые тесты визуализатора прошли на ура. Но при попытке подсунуть ему массив из 100*100*100 (или больше, точно не помню) клеток, каждый кадр отрисовывался вплоть до 8 секунд. Это не дело. Тут я вспомнил про пирамиду видимости. К сожалению, отрисовка по этой самой пирамиде занимала почти такое же время, так как большую часть времени пространство полностью было видно. При приближении к центру этого пространства и дельнейшем движении за него время отрисовки уменьшалось значительно.
Этап 3. Внешние воздействия
Время еще оставалось, а проект уже был готов к сдаче. Я понял, что чего-то не хватает. А вот чего именно – вопрос посложнее. Через некоторое время раздумий я решил, что мой КА совсем не похож на настоящую жизнь. Не хватает внешних факторов, влияющих на размножение клеток. В качестве такого фактора была выбрана температура.
Если кратко, то есть некая температура, назовем ее оптимальной, при которой выживаемость и рождаемость максимальные. При уменьшении и увеличении температуры выжить становится труднее. Но просто задать температуру было бы не интересно. И снова прибегнем к КА. В начальном состоянии температура сконцентрирована в центре пространства. С течением времени «теплый воздух» равномерно распределяется по всему пространству. Достигается это диффузией. Да не простой, а целочисленной. В данном случае это заключается в том, что некоторая часть температуры в клетке остается, а остальной частью соседние клетки обмениваются. Такой клеточный автомат уже не может быть синхронным, так как было ты странным, если бы все клетки одновременно поменялись… А чтобы его можно было запрограммировать под несколько процессов, необходимо прибегнуть к хитрости – перейти от асинхронного КА к блочно-синхронному. Смысл в том, что каждому процессу выделяется некоторый блок. Внутри этого блока КА является асинхронным. Но между собой блоки синхронизируются. На картинке клетки одного цвета просчитываются в одно время.

Целочисленная диффузия
#pragma omp parallel shared(Size, BlockSize, Int_Temp, PosCell, PosNbr, DiffKoeff)\
private(CellNum, NbrNum, x, y, z, Cell1, Cell2, Rem1, Rem2, Mov1, Mov2)
{
CellNum = rand() % 27;
#pragma omp for
for (x = 1; x < Size; x += BlockSize)
for (y = 1; y < Size; y += BlockSize)
for (z = 1; z < Size; z += BlockSize)
{
NbrNum = rand() % 6;
Cell1 = Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + Size) % Size];
Cell2 = Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size];
//DiffKoeff определяет, какой процент температуры
//останется в клетке, а какой перейдет в соседнюю.
Rem1 = Cell1 * (float)(1.0 - DiffKoeff);
Rem2 = Cell2 * (float)(1.0 - DiffKoeff);
Mov1 = Cell1 * DiffKoeff;
Mov2 = Cell2 * DiffKoeff;
if ((float)Cell1 * DiffKoeff - (float)Mov1 > (float)(rand() % 10) / 10.0)
Rem1++;
else if ((float)Cell1 * DiffKoeff - (float)Mov1)
Mov1++;
if ((float)Cell2 * DiffKoeff - (float)Mov2 > (float)(rand() % 10) / 10.0)
Rem2++;
else if ((float)Cell2 * DiffKoeff - (float)Mov2)
Mov2++;
Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + Size) % Size] = Mov2 + Rem1;
Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size] \
= Mov1 + Rem2;
}
}
Дальнейшие перспективы
Конечно, данная реализация не является идеальной. Код никак не оптимизирован. В первую очередь можно улучшить визуализатор. Помимо отсечения по пирамиде видимости добавить отсечение по Z-буферу, чтобы те клетки, которые скрыты клетками переднего плана, не рисовались.
Вообще, проект можно раздуть до космических масштабов. Например, хочется добавить дополнительные слои. Если говорить только о внешних воздействиях, то это может быть, например, рельеф. На больших высотах клетки будут находиться с меньшей вероятностью. К тому же, там будет холоднее. Можно добавить слой с растительностью, которая будет служить пищей. А можно клонировать слой с самими клетками и создать несколько видов организмов, которые будут друг друга поедать. Можно добавить мутации и многое-многое другое. Было бы желание.
Результаты
Теперь, наконец, можно перейти к самому интересному.
Сначала программа тестировалась без температурного слоя, так как к тому времени его просто не было. К сожалению, программа не имеет нормального интерфейса, и мне пришлось написать генератор тестов. Он не представляет особого интереса. Единственная его задача – сделать в центре игрового пространства кубик из клеток. Ниже представлены кубики 3х3х3, 4х4х4 и 5х5х5. Здесь представлены только некоторые шаги, чтоб сложилась общая картина происходящего.
3х3х3, шаг 1:

3х3х3, шаг 4:

3х3х3, шаги 5 и 6:

Получается довольно забавная мигалка.
4х4х4, шаг 1:

4х4х4, шаг 10:

4х4х4, шаг 100:

Дальше практически ничего не меняется.
5х5х5, шаг 1:

5х5х5, шаг 4:

5х5х5, шаг 7:

5х5х5, шаг 8:

На следующем шаге не остается ни одной живой клетки.
Теперь к кубику 4х4х4 добавим температуру. Температурный слой представлен в виде центрального среза. Красный цвет – оптимальная температура, желтый – чуть ниже нормы, розовый – низкая. Игровое пространство имеет размеры 50х50х50, в центре расположен куб 40х40х40 с оптимальной температурой. Вот что получилось.
Шаг 1:

Шаг 10:

Шаг 50:

Шаг 150:

Шаг 200:

Все предельно ясно: воздух остывает, жизнь прекращается.
К сожалению, самой программой поделиться не могу, так как входные данные жестко задаются в генераторе. Зато могу поделиться исходниками, но предупреждаю сразу: код просто ужасен.
Исходники