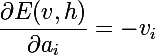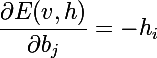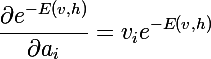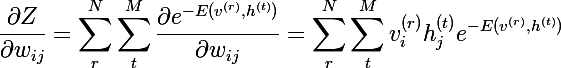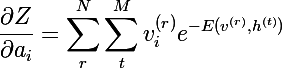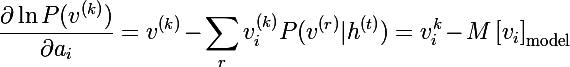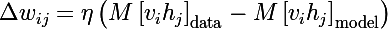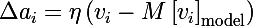Привет. Закончился курс по нейронным сетям. Хороший курс, но мало практики. Так что в этом посте мы рассмотрим, напишем и протестим ограниченную машину Больцмана — стохастическую, генеративную модель нейронной сети. Обучим ее, используя алгоритм Contrastive Divergence (CD-k), разработанный профессором Джеффри Хинтоном, который кстати и ведет тот курс. Тестировать мы будем на наборе печатных английских букв. В следующем посте будет рассмотрен один из недостатков алгоритма обратного распространения ошибки и способ первоначальной инициализации весов с помощью машины Больцмана. Кто не боится формулок и простыней текста, прошу под кат.
Я не буду особо заострять внимание на истории происхождения ограниченной машины Больцмана (RBM), упомяну лишь, что началось все с рекуррентных нейронных сетей, которые представляют из себя сети с обратной связью, которые крайне трудно обучить. Вследствие этого небольшого затруднения в обучении, народ стал выдумывать более ограниченные рекуррентные модели, для которых можно было бы применить более простые алгоритмы обучения. Одной из таких моделей была нейронная сеть Хопфилда, и он же ввел понятие энергии сети, сравнив нейросетевую динамику с термодинамикой:
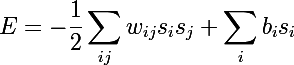
Следующим шагом на пути к RBM были обыкновенные машины Больцмана, они отличаются от сети Хопфилда тем, что имеют стохастическую природу, а нейроны поделены на две группы, описывающие обозреваемые и скрытые состояния (по аналогии со скрытыми моделями Маркова, кстати Хинтон признается в лекциях, что оттуда и позаимствовал слово «скрытый»). Энергия в машинах больцмана выражается следующим образом:
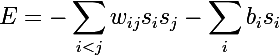
Машина Больцмана представляет из себя полносвязный неориентированный граф, и таким образом, любые две вершины из одной группы зависят друг от друга.
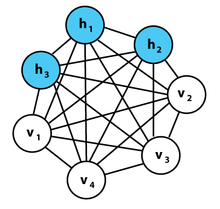
Но если убрать связи внутри группы, чтобы получился двудольный граф, мы получим структуру модели RBM.
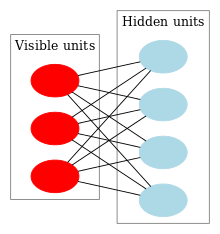
Особенность этой модели в том, что при данном состоянии нейронов одной группы, состояния нейронов другой группы будут независимы друг от друга. Теперь можно перейти к теории, где ключевую роль играет именно это свойство.
RBM интерпретируются аналогично скрытым моделям Маркова. У нас есть ряд состояний, которые мы можем наблюдать (видимые нейроны, которые предоставляют интерфейс для общения с внешней средой) и ряд состояний, которые скрыты, и мы не можем напрямую увидеть их состояние (скрытые нейроны). Но мы можем сделать вероятностный вывод относительно скрытых состояний, опираясь на состояния, которые мы можем наблюдать. Обучив такую модель, мы так же получаем возможность делать выводы относительно видимых состояний, зная скрытые (теорему Байеса никто не отменял =), и тем самым генерировать данные из того вероятностного распределения, на котором обучена модель.
Таким образом, мы можем сформулировать цель обучения модели: необходимо настроить параметры модели так, чтобы восстановленный вектор из исходного состояния был наиболее близок к оригиналу. Под восстановленным понимается вектор, полученный вероятностным выводом из скрытых состояний, которые в свою очередь получены вероятностным выводом из обозреваемых состояний, т.е. из оригинального вектора.
Введем следующие обозначения:
Мы будем рассматривать обучающее множество, состоящее из бинарных векторов, но это легко обобщается до векторов из действительных чисел. Предположим, что у нас n видимых нейронов и m скрытых. Введем понятие энергии для RBM:
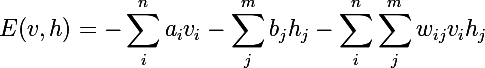
Нейросеть будет вычислять совместную вероятность всевозможных пар v и h следующим образом:

где Z — это статсумма или нормализатор (partition function) следующего вида (предположим, у нас имеется всего N образов v, и M образов h):

Очевидно, что полная вероятность вектора v будет вычисляться суммированием по всем h:

Рассмотрим вероятность того, что при данном v одно из скрытых состояний h_k = 1. Для этого представим один нейрон, тогда энергия системы при 1 будет E1, а при 0 будет E0, а вероятность 1 будет равна сигмоидной функции от линейной комбинации текущего нейрона с вектором состояний обозреваемого слоя вместе со смещением:
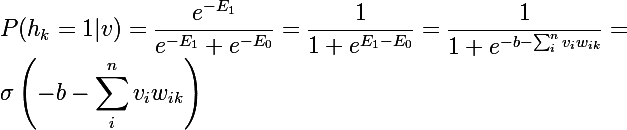
А так как при данном v все h_k не зависят друг от друга, то:

Аналогичный вывод делается и для вероятности v при данном h.
Как мы помним, цель обучения — это сделать так, чтобы восстановленный вектор был наиболее близок к оригиналу, или же, другими словами, максимизировать вероятность p(v). Для этого необходимо вычислить частные производные вероятности по параметрам модели. Начнем с дифференцирования энергии по параметрам модели:
Также нам понадобятся производные экспоненты от отрицательной энергии:
Продифференцируем статсумму:
Мы почти у цели -) Рассмотрим частную производную вероятности v по весам:
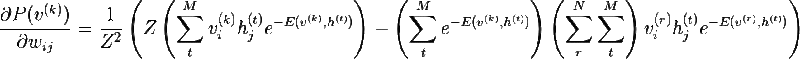
Очевидно, что максимизация вероятности это тоже самое, что максимизация логарифма вероятности, этот трюк поможет прийти к красивому решению. Рассмотрим производную натурального логарифма по весу:
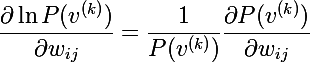
Объединяя две последние формулы, получаем следующее выражение:
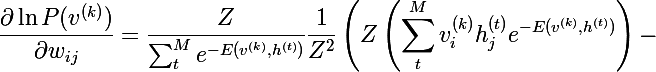
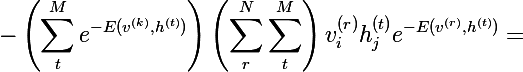

Домножив числитель и знаменатель каждого слагаемого на Z и, упростив до вероятностей, получим следующее выражение:

А по определению математического ожидания мы получаем итоговое выражение (M перед квадратной скобкой — это знак мат. ожидания):
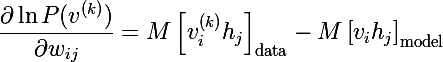
Аналогично выводятся и производные по смещениям нейронов:
И в итоге получаются три правила обновления параметров модели, где эта — это скорость обучения:
PS мог ошибиться малька в индексах, на хабре же нет встроенного редактора =)
редактора =)
Этот алгоритм придуман профессором Хинтоном в 2002 году, и он отличается своей простотой. Главная идея в том, что математические ожидания заменяются вполне определенными значениями. Вводится понятие процесса сэмплирования (Gibbs sampling, чтобы увидеть ассоциацию, можно заглянуть сюда). Процесс CD-k выглядит следующим образом:
В лекциях у Хинтона это выглядит так:

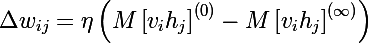
Т.е. чем дольше мы делаем сэмплинг, тем точнее будет наш градиент. В то же время профессор утверждает, что даже для CD-1 (всего одна итерация сэмплинга) уже вполне хороший результат получается. Первое слагаемое называется положительной фазой, а второе со знаком минус называется отрицательной фазой.
Как и в реализации алгоритма обратного распространения ошибки, я использую почти те же интерфейсы. Так что рассмотрим сразу же функцию обучения нейросети. Реализовывать обучение мы будем с использованием момента инерции.
Очень краткий экскурс в историю
Я не буду особо заострять внимание на истории происхождения ограниченной машины Больцмана (RBM), упомяну лишь, что началось все с рекуррентных нейронных сетей, которые представляют из себя сети с обратной связью, которые крайне трудно обучить. Вследствие этого небольшого затруднения в обучении, народ стал выдумывать более ограниченные рекуррентные модели, для которых можно было бы применить более простые алгоритмы обучения. Одной из таких моделей была нейронная сеть Хопфилда, и он же ввел понятие энергии сети, сравнив нейросетевую динамику с термодинамикой:
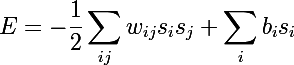
- w — вес между нейронами
- b — смещение нейрона
- s — состояние нейрона
Следующим шагом на пути к RBM были обыкновенные машины Больцмана, они отличаются от сети Хопфилда тем, что имеют стохастическую природу, а нейроны поделены на две группы, описывающие обозреваемые и скрытые состояния (по аналогии со скрытыми моделями Маркова, кстати Хинтон признается в лекциях, что оттуда и позаимствовал слово «скрытый»). Энергия в машинах больцмана выражается следующим образом:
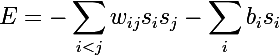
Машина Больцмана представляет из себя полносвязный неориентированный граф, и таким образом, любые две вершины из одной группы зависят друг от друга.

Но если убрать связи внутри группы, чтобы получился двудольный граф, мы получим структуру модели RBM.

Особенность этой модели в том, что при данном состоянии нейронов одной группы, состояния нейронов другой группы будут независимы друг от друга. Теперь можно перейти к теории, где ключевую роль играет именно это свойство.
Интерпретация и цель
RBM интерпретируются аналогично скрытым моделям Маркова. У нас есть ряд состояний, которые мы можем наблюдать (видимые нейроны, которые предоставляют интерфейс для общения с внешней средой) и ряд состояний, которые скрыты, и мы не можем напрямую увидеть их состояние (скрытые нейроны). Но мы можем сделать вероятностный вывод относительно скрытых состояний, опираясь на состояния, которые мы можем наблюдать. Обучив такую модель, мы так же получаем возможность делать выводы относительно видимых состояний, зная скрытые (теорему Байеса никто не отменял =), и тем самым генерировать данные из того вероятностного распределения, на котором обучена модель.
Таким образом, мы можем сформулировать цель обучения модели: необходимо настроить параметры модели так, чтобы восстановленный вектор из исходного состояния был наиболее близок к оригиналу. Под восстановленным понимается вектор, полученный вероятностным выводом из скрытых состояний, которые в свою очередь получены вероятностным выводом из обозреваемых состояний, т.е. из оригинального вектора.
Теория
Введем следующие обозначения:
- w_ij — веc между i-ым нейроном
- a_i — смещение видимого нейрона
- b_j — смещение скрытого нейрона
- v_i — состояние видимого нейрона
- h_j — состояние скрытого нейрона
Мы будем рассматривать обучающее множество, состоящее из бинарных векторов, но это легко обобщается до векторов из действительных чисел. Предположим, что у нас n видимых нейронов и m скрытых. Введем понятие энергии для RBM:
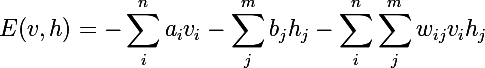
Нейросеть будет вычислять совместную вероятность всевозможных пар v и h следующим образом:

где Z — это статсумма или нормализатор (partition function) следующего вида (предположим, у нас имеется всего N образов v, и M образов h):

Очевидно, что полная вероятность вектора v будет вычисляться суммированием по всем h:

Рассмотрим вероятность того, что при данном v одно из скрытых состояний h_k = 1. Для этого представим один нейрон, тогда энергия системы при 1 будет E1, а при 0 будет E0, а вероятность 1 будет равна сигмоидной функции от линейной комбинации текущего нейрона с вектором состояний обозреваемого слоя вместе со смещением:
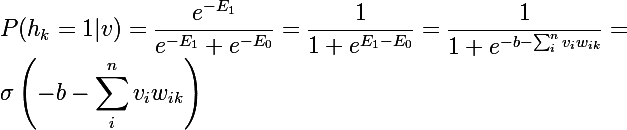
А так как при данном v все h_k не зависят друг от друга, то:

Аналогичный вывод делается и для вероятности v при данном h.
Как мы помним, цель обучения — это сделать так, чтобы восстановленный вектор был наиболее близок к оригиналу, или же, другими словами, максимизировать вероятность p(v). Для этого необходимо вычислить частные производные вероятности по параметрам модели. Начнем с дифференцирования энергии по параметрам модели:
Также нам понадобятся производные экспоненты от отрицательной энергии:
Продифференцируем статсумму:
Мы почти у цели -) Рассмотрим частную производную вероятности v по весам:
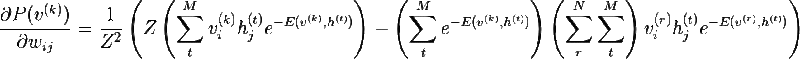
Очевидно, что максимизация вероятности это тоже самое, что максимизация логарифма вероятности, этот трюк поможет прийти к красивому решению. Рассмотрим производную натурального логарифма по весу:
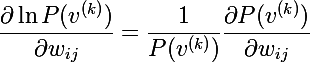
Объединяя две последние формулы, получаем следующее выражение:
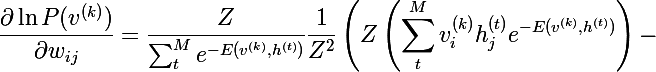
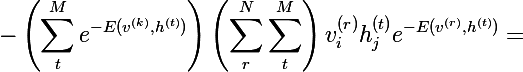

Домножив числитель и знаменатель каждого слагаемого на Z и, упростив до вероятностей, получим следующее выражение:

А по определению математического ожидания мы получаем итоговое выражение (M перед квадратной скобкой — это знак мат. ожидания):
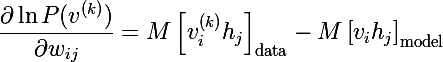
Аналогично выводятся и производные по смещениям нейронов:
И в итоге получаются три правила обновления параметров модели, где эта — это скорость обучения:
PS мог ошибиться малька в индексах, на хабре же нет встроенного
 редактора =)
редактора =) Алгоритм обучения Contrastive Divergence
Этот алгоритм придуман профессором Хинтоном в 2002 году, и он отличается своей простотой. Главная идея в том, что математические ожидания заменяются вполне определенными значениями. Вводится понятие процесса сэмплирования (Gibbs sampling, чтобы увидеть ассоциацию, можно заглянуть сюда). Процесс CD-k выглядит следующим образом:
- состояние видимых нейронов приравнивается к входному образу
- выводятся вероятности состояний скрытого слоя
- каждому нейрону скрытого слоя ставится в соответствие состояние «1» с вероятностью, равной его текущему состоянию
- выводятся вероятности видимого слоя на основании скрытого
- если текущая итерация меньше k, то возврат к шагу 2
- выводятся вероятности состояний скрытого слоя
В лекциях у Хинтона это выглядит так:

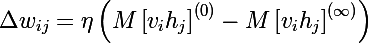
Т.е. чем дольше мы делаем сэмплинг, тем точнее будет наш градиент. В то же время профессор утверждает, что даже для CD-1 (всего одна итерация сэмплинга) уже вполне хороший результат получается. Первое слагаемое называется положительной фазой, а второе со знаком минус называется отрицательной фазой.
Talk is cheap. Show me the code.
Как и в реализации алгоритма обратного распространения ошибки, я использую почти те же интерфейсы. Так что рассмотрим сразу же функцию обучения нейросети. Реализовывать обучение мы будем с использованием момента инерции.
public void Train(IMultilayerNeuralNetwork network, IList<DataItem> data)
Я использую класс с конфигурацией алгоритма обучения, перечислю параметры. Я старался откомментить все в коде, чтобы поменьше текста вписывать в текст поста.
LearningAlgorithmConfig config = new LearningAlgorithmConfig()
{
BatchSize = 10, //размер батча
MaxEpoches = 1000, //максимальное количество эпох до остановки алгоритма
GibbsSamplingChainLength = 30, //как раз параметр k из CD-k
LearningRate = 0.01, //скорость обучения
CostFunctionRecalculationStep = 1, //как часто вычислять ошибку обучения
Momentum = 0.9, //параметр момента
MinError = 0, // минимальная ошибка для остановки алгоритма
MinErrorChange = 0, //минимальное изменение ошибки для остановки алгоритма
UseBiases = true //использовать ли смещения в процессе обучения
};
Перед основным циклом обучения инициализируются различные параметры.
Инициализация
ILayer visibleLayer = network.Layers[0]; //сеть RBM состоит из двух слоев, один это видимые состояния
ILayer hiddenLayer = network.Layers[1]; //и один скрытые состояния
if (!_config.UseBiases) //случай когда смещения учавствуют в обучении
{
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
visibleLayer.Neurons[i].Bias = 0d;
}
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
hiddenLayer.Neurons[i].Bias = 0d;
}
}
//init momentum
//формулу для момента я приведу далее при обновлении весов
double[,] momentumSpeedWeights = new double[visibleLayer.Neurons.Length, hiddenLayer.Neurons.Length];
double[] momentumSpeedVisibleBiases = new double[visibleLayer.Neurons.Length];
double[] momentumSpeedHiddenBiases = new double[hiddenLayer.Neurons.Length];
//init stop factors
bool stopFlag = false;
double lastError = Double.MaxValue; //многие переменные имеют говорящие имена, так что пропущу их описание
double lastErrorChange = double.MaxValue;
double learningRate = _config.LearningRate;
int currentEpoche = 0;
BatchEnumerator<DataItem<double>> batchEnumerator = new BatchEnumerator<DataItem<double>>(data, _config.BatchSize, true);
Текст BatchEnumerator'а можно посмотреть тут, а про батчи описано в предыдущем посте.
Далее начинается основной цикл по эпохам:
Основной цикл
do
{
DateTime dtStart = DateTime.Now;
//start batch processing
foreach (IList<DataItem<double>> batch in batchEnumerator)
{
//batch gradient
//как и в реализации алгоритма обратного распространения из предыдущей статьи, в набле хранится изменения весов/смещений на один батч
double[,] nablaWeights = new double[visibleLayer.Neurons.Length, hiddenLayer.Neurons.Length];
double[] nablaHiddenBiases = new double[hiddenLayer.Neurons.Length];
double[] nablaVisibleBiases = new double[visibleLayer.Neurons.Length];
#region iterate through batch
//...
#endregion
#region compute mean of wights nabla, and update them
//...
#endregion
}
#region Logging and error calculation
//...
#endregion
//условия остановки алгоритма
currentEpoche++;
if (currentEpoche >= _config.MaxEpoches)
{
stopFlag = true;
Logger.Instance.Log("Stop: currentEpoche:" + currentEpoche + " >= _config.MaxEpoches:" + _config.MaxEpoches);
}
else if (_config.MinError >= lastError)
{
stopFlag = true;
Logger.Instance.Log("Stop: _config.MinError:" + _config.MinError + " >= lastError:" + lastError);
}
else if (_config.MinErrorChange >= lastErrorChange)
{
stopFlag = true;
Logger.Instance.Log("Stop: _config.MinErrorChange:" + _config.MinErrorChange + " >= lastErrorChange:" + lastErrorChange);
}
} while (!stopFlag);
Рассмотрим основную часть алгоритма, это как раз Gibbs sampling, вычисление и аккумулирование градиента по параметрам.
#region iterate through batch
//проходим по каждому обучающему примеру из одного батча
foreach (DataItem<double> dataItem in batch)
{
//init visible layer states
//присваиваем обозримым состояниям значения из одного/текущего примера из батча
for (int i = 0; i < dataItem.Input.Length; i++)
{
visibleLayer.Neurons[i].LastState = dataItem.Input[i];
}
#region Gibbs sampling
for (int k = 0; k <= _config.GibbsSamplingChainLength; k++)
{
//calculate hidden states probabilities
//скрытый слой обновляет свои состояния используя состояния обозримого слоя и параметры модели, вычисляются пока только вероятности
hiddenLayer.Compute();
#region accumulate negative phase
//в случае если текущая итерация сэмплинга - это последняя итерация, то необходимо собрать отрицательную часть градиента
if (k == _config.GibbsSamplingChainLength)
{
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
for (int j = 0; j < hiddenLayer.Neurons.Length; j++)
{
//умножение видимых состояний на скрытые
nablaWeights[i, j] -= visibleLayer.Neurons[i].LastState *
hiddenLayer.Neurons[j].LastState;
}
}
if (_config.UseBiases)
{
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
nablaHiddenBiases[i] -= hiddenLayer.Neurons[i].LastState;
}
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
nablaVisibleBiases[i] -= visibleLayer.Neurons[i].LastState;
}
}
break;
}
#endregion
//sample hidden states
//после того как вычислены вероятности, необходимо сделать сэмплирование скрытого слоя, но только если это не последняя итерация, иначе мы бы уже вышли из цикла Gibbs sampling
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
hiddenLayer.Neurons[i].LastState = _r.NextDouble() <= hiddenLayer.Neurons[i].LastState ? 1d : 0d;
}
#region accumulate positive phase
//если это первая итерация, то собираем положительную часть градиента
if (k == 0)
{
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
for (int j = 0; j < hiddenLayer.Neurons.Length; j++)
{
nablaWeights[i, j] += visibleLayer.Neurons[i].LastState*
hiddenLayer.Neurons[j].LastState;
}
}
if (_config.UseBiases)
{
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
nablaHiddenBiases[i] += hiddenLayer.Neurons[i].LastState;
}
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
nablaVisibleBiases[i] += visibleLayer.Neurons[i].LastState;
}
}
}
#endregion
//calculate visible probs
//вычисляем вероятности видимого слоя
visibleLayer.Compute();
//сэмплирование видимого слоя, в статье у Хинтона написано что его сэмплировать вообще говоря не обязательно, от этого только увеличивается дисперсия, но мат. ожидание остается на месте; мои опыты показали что без этого блока работает действительно лучше
//todo: may be not do sampling, like in 3.2 of http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf
//sample visible
//for (int i = 0; i < visibleLayer.Neurons.Length; i++)
//{
// visibleLayer.Neurons[i].LastState = _r.NextDouble() <= visibleLayer.Neurons[i].LastState ? 1d : 0d;
//}
}
#endregion
}
Мы вышли из цикла по обучающим примерам из батча, и нужно обновить веса. Момент используется следующим образом: прошлое изменение параметра модели умножается на постоянную момента (мю) и складывается с текущим градиентом. Затем сумма умножается на скорость обучения.

#region compute mean of wights nabla, and update them
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
for (int j = 0; j < hiddenLayer.Neurons.Length; j++)
{
//запись текущего изменения веса с учетом прошлого, для использования на следующей итерации
momentumSpeedWeights[i, j] = _config.Momentum*momentumSpeedWeights[i, j] +
nablaWeights[i, j]/batch.Count;
//использование текущего изменения веса и скорости обучения
visibleLayer.Neurons[i].Weights[j] += learningRate * momentumSpeedWeights[i, j];
hiddenLayer.Neurons[j].Weights[i] = visibleLayer.Neurons[i].Weights[j];
}
}
if (_config.UseBiases)
{
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
momentumSpeedHiddenBiases[i] = _config.Momentum*momentumSpeedHiddenBiases[i] +
nablaHiddenBiases[i]/batch.Count;
hiddenLayer.Neurons[i].Bias += learningRate * momentumSpeedHiddenBiases[i];
}
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
momentumSpeedVisibleBiases[i] = _config.Momentum*momentumSpeedVisibleBiases[i] +
nablaVisibleBiases[i]/batch.Count;
visibleLayer.Neurons[i].Bias += learningRate * momentumSpeedVisibleBiases[i];
}
}
Осталось вывести какую-либо сопутствующую информацию. В основе модели лежит энергия, но стоит помнить, что минимизация/максимизация энергии не означает улучшения восстанавливающей способности, мы ведь максимизируем вероятность того, что восстановленный вектор будет такой же, как оригинальный. Есть другой способ: подсчитывать Евклидово расстояние между восстановленным вектором и оригинальным. Очевидно, что это значение будет падать не монотонно, а частенько осциллировать, но в целом будет заметно уменьшение этого значения. В следующем разделе я приведу пример лога.
#region Logging and error calculation
string msg = "Epoche #" + currentEpoche;
#region calculate error
if (currentEpoche % _config.CostFunctionRecalculationStep == 0)
{
#region calculating squared error with reconstruction
IMetrics<double> sed = MetricsCreator.SquareEuclideanDistance();
double d = 0;
foreach (DataItem<double> dataItem in data)
{
d += sed.Calculate(dataItem.Input, network.ComputeOutput(dataItem.Input));
}
msg += "; SqDist is " + d;
lastErrorChange = Math.Abs(lastError - d);
lastError = d;
#endregion
}
#endregion
msg += "; Time: " + (DateTime.Now - dtStart).Duration().ToString();
Logger.Instance.Log(msg);
Исходник можно посмотреть тут.
Результаты работы RBM
Свои эксперименты я делал на распознавании текста. Для этого поста я выбрал простое, небольшого размера множество больших английских букв, что бы ускорить процесс обучения, в котором присутствуют немного шумов (всего 260 картинок 29 на 29 пикселей): скачать для просмотра можно тут.
Обучение производилось со следующими параметрами:
LearningAlgorithmConfig:
LearningRate = 0.01
BatchSize = 10
RegularizationFactor = 0
MaxEpoches = 1000
MinError = 0
MinErrorChange = 0
CostFunctionRecalculationStep = 1
ErrorFunction =
Momentum = 0.9
NeuronLocalGainLimit: not setted
GibbsSamplingChainLength = 30
UseBiases = True
Как видно, единственным критерием остановки было 1000 эпох. Т.к. батч равен 10, то за одну эпоху было сделано 26 обновлений весов, а в общем 26000 обновлений. Лог можно скачать тут.
По логу можно увидеть, что после первой эпохи (26 обновлений параметров) среднеквадратичное Евклидово расстояние равно 13128, а на последней уже 76.
Давайте глянем на несколько восстановленных картинок (слева оригинал, справа восстановленное):

А теперь давайте посмотрим на одно из изображений покрупнее:
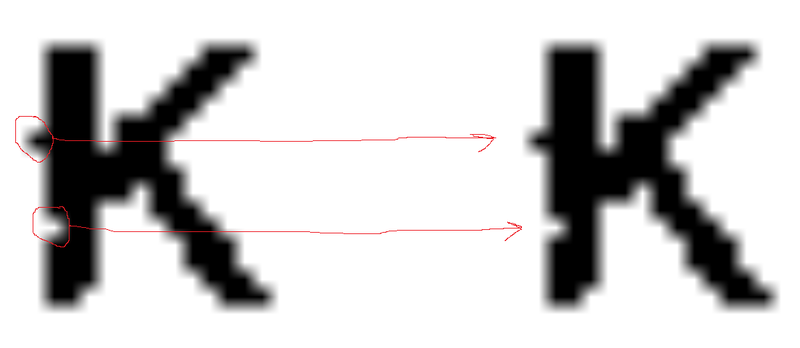
Как видно по картинке, даже шумы восстанавливаются правильно (мы сейчас не говорим о понятии переобучения для RBM).
Теперь зададимся вопросом, можно ли как-то визуализировать паттерны, которые были найдены сетью. Оказывается, это просто. Для каждого скрытого состояния есть 841 (29*29) вес и одно смещение. Если проигнорировать смещение, то из 841 веса можно составить картинку 29 на 29 пикселей, и это как раз будут нужные нам шаблоны, автоматически найденные сетью. А ведь линейная комбинация шаблона и картинки плюс смещение, и взятая от этого числа сигмоидная функция, и будет вероятность того, активен нейрон или нет. Вот полученная карта:

А вот как выглядит эта же карта у крутых пацанов на множестве рукописных символов MNIST: http://deeplearning.net/tutorial/_images/filters_at_epoch_14.png. Так что мне еще подбирать и подбирать параметры обучения, но вроде как я на правильном пути =)
В следующем посте мы рассмотрим применение RBM для того, чтобы инициализировать веса сети прямого распространения, которая будет обучаться по алгоритму обратного распространения ошибки.
Ссылки
- https://class.coursera.org/neuralnets-2012-001/
- http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf
- http://deeplearning.net/tutorial/rbm.html#contrastive-divergence-cd-k
- http://www.iro.umontreal.ca/~lisa/twiki/bin/view.cgi/Public/DBNEquations
- http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
- ну и педивикия конечно
PS респект и уважуха пользователю ambikontur за регулярную помощь в проверке формул и текста!
UPD:
вот кстати паттерны полученные после более тонкой настройки и на множестве состоящем из нескольких шрифтов

и если немного увеличить