 История этой демки такова: однажды один мой друг сделал для своей игры генератор карт планет и захотел, чтобы созданные таким образом карты показывались в виде вращающейся сферы. Однако, при этом он не хотел использовать 3D-графику, а вместо этого сгенерировал множество кадров с этой самой сферой, повёрнутой на разные углы. Количество используемой памяти было… скажем так, избыточным, ну а скорость генерации кадров (как и качество их исполнения) сильно страдала. Чуть подумав, мне удалось помочь ему оптимизировать этот процесс, но в целом меня не покидало справедливое ощущение того, что это задача для OpenGL, а вовсе не для 2D-графики.
История этой демки такова: однажды один мой друг сделал для своей игры генератор карт планет и захотел, чтобы созданные таким образом карты показывались в виде вращающейся сферы. Однако, при этом он не хотел использовать 3D-графику, а вместо этого сгенерировал множество кадров с этой самой сферой, повёрнутой на разные углы. Количество используемой памяти было… скажем так, избыточным, ну а скорость генерации кадров (как и качество их исполнения) сильно страдала. Чуть подумав, мне удалось помочь ему оптимизировать этот процесс, но в целом меня не покидало справедливое ощущение того, что это задача для OpenGL, а вовсе не для 2D-графики.И вот, однажды, когда меня мучила бессонница, я решил попробовать совместить эти два подхода: нарисовать вращающуюся сферу (с натянутой на неё картой планеты) через OpenGL, но при этом оставив её плоской.
И должен сказать, что у меня это получилось. Но обо всём по порядку.
Математика процесса
Для начала определимся с собственно задачей. Для каждой точки на экране у нас имеются две экранные координаты в декартовой системе координат, и нам необходимо найти для неё сферические координаты (фактически, широту и долготу), которые по сути и являются текстурными координатами для карты планеты.
Итак. Переход от сферической системы координат к декартовой задаётся системой уравнений (взято с Википедии):
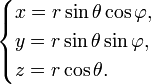
а обратный переход — такими уравнениями:

Координату Z мы легко можем получить из X и Y, зная радиус, а сам радиус мы можем принять равным единице.
В дальнейшем договоримся о том, что приведённые выше уравнения мы слегка изменим, поменяв местами понятия Y (у нас это будет экранная вертикаль) и Z (это будет глубина сцены).
Техническая часть
Реализация идеи потребует от нас применения квада (я уже писал о том, как его использовать, поэтому повторяться не буду, тем более что ниже приведена ссылка на полный исходный код проекта), а также двух текстур: собственно карты планеты (я использовал текстуру Земли размера 2048x1024) и карты текстурных координат. Код генерации второй текстуры аккуратно повторяет математику преобразования из декартовых координат в сферические:
int texSize = 1024;
double r = texSize * 0.5;
int[] pixels = new int[texSize * texSize];
for (int row = 0, idx = 0; row < texSize; row++) {
double y = (r - row) / r;
double sin_theta = Math.sqrt(1 - y*y);
double theta = Math.acos(y);
long v = Math.round(255 * theta / Math.PI);
for (int col = 0; col < texSize; col++) {
double x = (r - col) / r;
long u = 0, a = 0;
if (x >= -sin_theta && x <= sin_theta) {
double z = Math.sqrt(1 - y*y - x*x);
double phi = Math.atan2(z, x);
u = Math.round(255 * phi / (2 * Math.PI));
a = Math.round(255 * z);
}
pixels[idx++] = (int) ((a << 24) + (v << 8) + u);
}
}
GLES20.glGenTextures(1, genbuf, 0);
offsetTex = genbuf[0];
if (offsetTex != 0) {
GLES20.glBindTexture(GLES20.GL_TEXTURE_2D, offsetTex);
GLES20.glTexParameteri(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_MIN_FILTER, GLES20.GL_NEAREST);
GLES20.glTexParameteri(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_MAG_FILTER, GLES20.GL_NEAREST);
GLES20.glTexParameteri(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_WRAP_S, GLES20.GL_NONE);
GLES20.glTexParameteri(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_WRAP_T, GLES20.GL_NONE);
GLES20.glTexImage2D(GLES20.GL_TEXTURE_2D, 0, GLES20.GL_RGBA, texSize, texSize, 0, GLES20.GL_RGBA, GLES20.GL_UNSIGNED_BYTE, IntBuffer.wrap(pixels));
}
Отметим, что координаты X и Y переводятся из диапазона [0..texSize] в диапазон [-1..1], а текстурные координаты U и V переводятся из радианов в диапазон [0..255], после чего записываются соответственно в красную и зелёную компоненты 32-битной текстуры. Альфа-канал используется для сохранения «глубины» (координаты Z), а синий пока остаётся незадействованным. Отключение билинейной фильтрации также не случайно: на данном этапе она не даёт какого-либо эффекта (соседние точки в любом случае имеют одни и те же значения, с довольно резкими скачками), а в том, что я собираюсь показать дальше, она и вовсе будет вредна. Но об этом ниже.
 Обе текстуры подаются на вход простого пиксельного шейдера (здесь и далее картинки кликабельны):
Обе текстуры подаются на вход простого пиксельного шейдера (здесь и далее картинки кликабельны):private final String quadFS =
"precision mediump float;\n" +
"uniform sampler2D uTexture0;\n" +
"uniform sampler2D uTexture1;\n" +
"varying vec4 TexCoord0;\n" +
"void main() {\n" +
" vec4 vTex = texture2D(uTexture0, TexCoord0.xy);\n" +
" vec3 vCol = texture2D(uTexture1, vTex.xy).rgb;\n" +
" gl_FragColor = vec4(vCol, (vTex.w > 0.0 ? 1.0 : 0.0));\n" +
"}\n";
Код отрисовки сцены я не привожу, т.к. в нём всё довольно тривиально (и, опять же, его можно посмотреть в полном исходнике), да и сам шейдер довольно примитивен. Самое любопытное в нём, пожалуй, то, что альфа-канал пока лишь проверяется на положительность, тогда как можно было бы задействовать его для эффекта освещения.
Получилось уже довольно неплохо, однако как-то плоско, плюс хотелось бы добавить собственно вращение планеты вокруг своей оси.
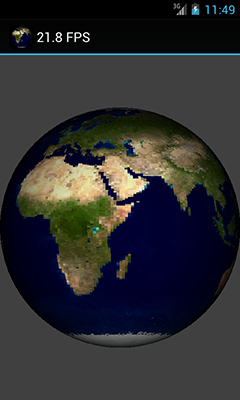 Включаем в шейдер ещё один параметр (будем менять его в зависимости от времени в диапазоне [0..1]), плюс добавляем «глубину» (умножение цвета на значение из альфа-канала):
Включаем в шейдер ещё один параметр (будем менять его в зависимости от времени в диапазоне [0..1]), плюс добавляем «глубину» (умножение цвета на значение из альфа-канала):private final String quadFS =
"precision mediump float;\n" +
"uniform sampler2D uTexture0;\n" +
"uniform sampler2D uTexture1;\n" +
"uniform float uOffset;\n" +
"varying vec4 TexCoord0;\n" +
"void main() {\n" +
" vec4 vTex = texture2D(uTexture0, TexCoord0.xy);\n" +
" vTex.x += uOffset;\n" +
" vec3 vCol = texture2D(uTexture1, vTex.xy).rgb;\n" +
" gl_FragColor = vec4(vCol * vTex.w, (vTex.w > 0.0 ? 1.0 : 0.0));\n" +
"}\n";
Что ж, к самой сфере претензий нет, однако картинка выглядит как-то… восьмибитно, что ли. И неудивительно: мы же записывали текстурные координаты в диапазоне [0..255] (максимум, доступный нам в обычных цветовых компонентах), а значит наша текстура может иметь не больше 256 точек в высоту (и 512 в ширину, учитывая вращение). Маловато, нужна как минимум 10-битная точность.
Увеличиваем разрешение
Сразу предупреждаю: описанный здесь код может криво работать на каких-либо устройствах, хотя мне удалось добиться нормальной отрисовки на всех устройствах, которые я смог подержать в руках. В любом случае, описанное здесь является обычным хаком.
Итак, у нас пока задейстованы две из трёх цветовых компоненты, т.е. 16 бит из 24. Ну так упакуем же данные так, чтобы каждая текстурная координата имела размер 12 бит, что позволит нам работать с текстурами размером до 4096 пикселей в высоту! Для этого изменим буквально три строчки в программе:
...
long v = Math.round(4095 * theta / Math.PI);
...
u = Math.round(4095 * phi / (2 * Math.PI));
...
pixels[idx++] = (int) ((a << 24) + (v << 12) + ((u & 15) << 8) + (u >> 4));
...
и напишем новый шейдер, учитывающий 12-битную схему адресации (именно в этом месте необходимо, чтобы билинейная фильтрация была отключена!):
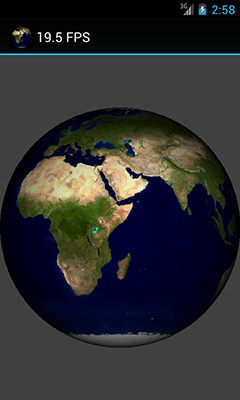
private final String quadFS =
"precision mediump float;\n" +
"uniform sampler2D uTexture0;\n" +
"uniform sampler2D uTexture1;\n" +
"uniform float uOffset;\n" +
"varying vec4 TexCoord0;\n" +
"void main() {\n" +
" vec4 vTex = texture2D(uTexture0, TexCoord0.xy);\n" +
" vec3 vOff = vTex.xyz * 255.0 + vec3(0.5, 0.5, 0.5);\n" +
" float hiY = floor(vOff.y / 16.0);\n" +
" float loY = vOff.y - 16.0 * hiY;\n" +
" vec2 vCoord = vec2(\n" +
" (vOff.x * 16.0 + loY) / 4095.0 + uOffset,\n" +
" (vOff.z * 16.0 + hiY) / 4095.0);\n" +
" vec3 vCol = texture2D(uTexture1, vCoord).rgb;\n" +
" gl_FragColor = vec4(vCol * vTex.w, (vTex.w > 0.0 ? 1.0 : 0.0));\n" +
"}\n";
Ну это же совсем другое дело! С небольшими изменениями (добавив масштабирование «щипком» и вращение пальцем) я эту программу показывал своим друзьям и колегам, и при этом спрашивал, сколько, по их мнению, в этой сцене треугольников. Результаты варьировались, да и сам вопрос вызывал подозрение в наличии подвоха (в этом случае респонденты шутили «один», что было недалеко от истины), но правильный ответ стабильно удивлял. И все, как один, спрашивали: а почему сферу можно крутить вокруг одной оси, но нельзя наклонять?.. Хм.
Наклон
А дело в том, что наклон в этой схеме реализовать существенно труднее. На самом деле, задача не является неразрешимой, и я с ней даже справился, но не обошлось без нюансов.
В сущности, задача сводится к тому, чтобы взять смещённую координату V, тогда как координата U не меняется: это происходит потому, что мы добавляем вращение вокруг оси X. План такой: преобразуем текстурные координаты в экранные (в диапазоне [-1..1]), применяем к ним матрицу поворота вокруг горизонтальной оси (для этого заранее запишем в новую константу uTilt синус и косинус угла наклона), а дальше воспользуемся новой координатой Y для выборки в нашей шаблонной текстуре. «Повёрнутая» координата Z нам тоже пригодится, с её помощью мы отзеркалим долготу для обратной стороны шарика). Экранную координату Z придётся посчитать явно, чтобы не делать две текстурных выборки из одной текстуры, заодно это повысит её точность.

private final String quadFS =
"precision mediump float;\n" +
"uniform sampler2D uTexture0;\n" +
"uniform sampler2D uTexture1;\n" +
"uniform float uOffset;\n" +
"uniform vec2 uTilt;\n" +
"varying vec4 TexCoord0;\n" +
"void main() {\n" +
" float sx = 2.0 * TexCoord0.x - 1.0;\n" +
" float sy = 2.0 * TexCoord0.y - 1.0;\n" +
" float z2 = 1.0 - sx * sx - sy * sy;\n" +
" if (z2 > 0.0) {;\n" +
" float sz = sqrt(z2);\n" +
" float y = (sy * uTilt.y - sz * uTilt.x + 1.0) * 0.5;\n" +
" float z = (sy * uTilt.x + sz * uTilt.y);\n" +
" vec4 vTex = texture2D(uTexture0, vec2(TexCoord0.x, y));\n" +
" vec3 vOff = vTex.xyz * 255.0 + vec3(0.5, 0.5, 0.5);\n" +
" float hiY = floor(vOff.y / 16.0);\n" +
" float loY = vOff.y - 16.0 * hiY;\n" +
" vec2 vCoord = vec2(\n" +
" (vOff.x * 16.0 + loY) / 4095.0,\n" +
" (vOff.z * 16.0 + hiY) / 4095.0);\n" +
" if (z < 0.0) { vCoord.x = 1.0 - vCoord.x; }\n" +
" vCoord.x += uOffset;\n" +
" vec3 vCol = texture2D(uTexture1, vCoord).rgb;\n" +
" gl_FragColor = vec4(vCol * sz, 1.0);\n" +
" } else {\n" +
" gl_FragColor = vec4(0.0, 0.0, 0.0, 0.0);\n" +
" }\n" +
"}\n";
Ура, наклон удался! Вот только странный шум на границе полушарий немного смущает. Очевидно, проблема кроется в недостаточной точности адресации в граничных точках (точки на самой окружности соответствуют слишком большому диапазону координат, один тексель расползается на интервал довольно заметной длины). В конце концов, мне удалось это победить, используя две сгенерированных текстуры вместо одной.
В итоге, можно приближать и крутить шарик почти так же, как в Google Earth. С тем отличием, что здесь — всего-навсего два треугольника.
Ну и, наконец, обещанное. Исходный код проекта доступен на GitHub.
Также можно скачать готовый .apk-файл.
Кстати, исходники для моих прошлых постов доступны там же.
Update: Кажется, мне всё-таки удалось добиться точного текстурирования на всех устройствах, это потребовало немного изменить порядок битов, а также немного подкорректировать округление цветов шаблонной текстуры. Теперь даже насильно сжатые текстуры должны работать более-менее нормально. Код на GitHub обновлён, новые .apk-файлы залиты.
Update 2: Всё-таки артефакт на границе полушарий был побеждён. Исходники и готовый .apk обновлены.
Кроме того, я добавил ещё один бонус: WebGL-версия этой демки доступна здесь.