 Привет. В этом посте мы рассмотрим простую модель фильтрации спама с помощью наивного байесовского классификатора с размытием по Лапласу, напишем несколько строк кода на R, и, наконец, протестируем на англоязычной базе данных смс спама. Вообще, на хабре я нашел две статьи посвященные данной теме, но ни в одной не было наглядного примера, чтобы можно было скачать код и посмотреть результат. Также не было упоминания про размытие, что существенно увеличивает качество модели, без особых затрат усилий, в отличие, скажем, от сложной предобработки текста. Но вообще, запилить очередной пост про наивного байеса меня побудило то, что я пишу методичку для студентов с примерами кода на R, вот и решил поделиться инфой.
Привет. В этом посте мы рассмотрим простую модель фильтрации спама с помощью наивного байесовского классификатора с размытием по Лапласу, напишем несколько строк кода на R, и, наконец, протестируем на англоязычной базе данных смс спама. Вообще, на хабре я нашел две статьи посвященные данной теме, но ни в одной не было наглядного примера, чтобы можно было скачать код и посмотреть результат. Также не было упоминания про размытие, что существенно увеличивает качество модели, без особых затрат усилий, в отличие, скажем, от сложной предобработки текста. Но вообще, запилить очередной пост про наивного байеса меня побудило то, что я пишу методичку для студентов с примерами кода на R, вот и решил поделиться инфой.Наивный байесовский классификатор
Рассмотрим множество некоторых объектов D = {dq, d2, ..., dm}, каждый из которых обладает некоторым набором признаков из множества всех признаков F = {f1, f2, ..., fq}, а также одной меткой из множества меток C = {c1, c2, ..., cr}. Нашей задачей является вычисление наиболее вероятного класса/метки входящего объекта d, опираясь на набор его признаков Fd = {fd1, fd2, ..., fdn}. Другими словами, нам необходимо вычислить такое значение случайной переменной C, при котором достигается апостериорный максимум (maximum a posteriori probability, MAP).

- 2.1 — собственно, это наша цель
- 2.2 — раскладываем по теореме Байеса
- 2.3 — учитывая, что мы ищем аргумент, максимизирующий функцию правдоподобия, и то, что знаменатель не зависит от этого аргумента и является в данном случае константой, то мы можем смело вычеркнуть значение полной вероятности P(d)
- 2.4 — так как логарифм монотонно возрастает для любого x > 0, то максимум любой функции f(x) будет идентичен максимуму ln(f(x)); это нужно для того, чтобы в будущем во время программирования не оперировать с числами, близкими к нулю
Модель наивного байесовского классификатора принимает два допущения, от того она такая и наивная:
- порядок следования признаков объекта не имеет значения;
- вероятности признаков не зависят друг от друга при данном классе:
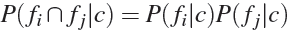 .
.
Учитывая вышеприведенные допущения, продолжим вывод формул.
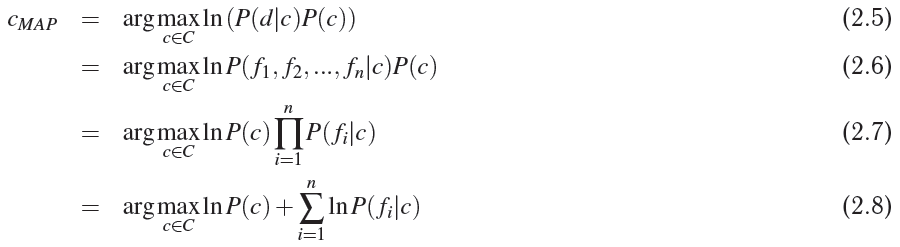
- 2.6-2.7 — это как раз следствие применения допущений
- 2.8 — здесь, как раз, применяется замечательное свойство логарифма, что позволяет нам избежать потери точности при оперировании очень маленькими значениями
Мы можем изобразить графическую модель наивного байесовского классификатора следующим образом:
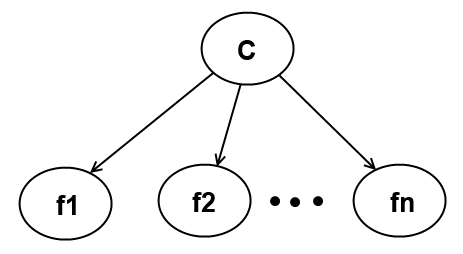
Спам классификатор
Теперь от более общей задачи классификации погрузимся в конкретную задачу классификации спама. Итак, мнжество D состоит из смс сообщений. Каждое сообщение помечено меткой из множества C = {ham, spam}. Для того что бы сформулировать понятие признаков, мы будем использовать модель представления bag of words, проиллюстируем это на примере. Допустим, у нас всего два ham смс сообщения в базе
hi how are youhow old are youТогда мы можем построить таблицу
| Слово | Частота |
|---|---|
| hi | 1 |
| how | 2 |
| are | 2 |
| you | 2 |
| old | 1 |
Всего 8 слов в корпусе не-спам сообщений, тогда после нормирования мы получим апостериорную вероятность слова, используя maximum likelihood estimation. Для примера вероятность слова «how» при условии, что сообщение не является спамом, будет такая:
P(fi = «how» | C = ham) = 2/8 = 1/4
Или же мы можем записать этот метод в общем виде:
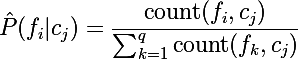 , где q — общее количество уникальных слов в словаре.
, где q — общее количество уникальных слов в словаре.Размытие по Лапласу
В этот момент самое время обратить внимание на следующую проблему. Вспомним нашу базу из двух ham сообщений, и, допустим, к нам пришло на классификацию сообщение: "hi bro", и, допустим, априорная вероятность не-спама P(ham) = 1/2. Вычислим вероятности слов:
- P(«hi» | ham) = 1/8
- P(«bro» | ham) = 0/8 = 0
Вспомним формулу 2.8 и вычислим выражение, находящееся под argmax при c = ham:
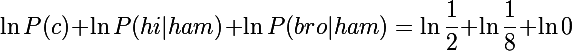
Очевидно, что мы получим либо ошибку либо отрицательную бесконечность, т.к. логарифм в нуле не существует. Если бы мы не использовали логарифмирование, то мы бы получили просто 0, т.е. вероятность этого сообщения была бы равна нулю, что в принципе большой пользы нам дает.
Избежать этого позволяет размытие по Лапласу или k-additive smoothing — этот метод позволяет делать размытие при вычислении вероятностей категорийных данных. В нашем случае это будет выглядеть следующим образом:
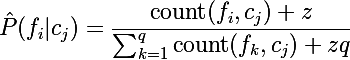 , где z >= 0 — коэффициент размытия, а q — это количество значений, которые может принимать случайная величина, в нашем случае ей является количество слов в классе; а q — общее количество слов которые были использованы при обучении модели.
, где z >= 0 — коэффициент размытия, а q — это количество значений, которые может принимать случайная величина, в нашем случае ей является количество слов в классе; а q — общее количество слов которые были использованы при обучении модели.Допустим, всего при прочтении ham и spam сообщений мы нашли 10 уникальных слов, тогда P(«hi» | ham) = ( 1 + 1 ) / (8 + 1*10 ) = 2/18 = 1/9 при коэффициенте размытия z = 1. А нулевая вероятность перестает быть таковой: P(«bro» | ham) = ( 0 + 1) / (8 + 1*10) = 1/18.
С Байесовской точки зрения, данный метод соответствует математическому ожиданию апостериорного распределения, используя в качестве априорного распределения — распределение Дирихле, параметризируемое параметром z.
Эксперимент и код
Я использую базу данных, скачанную с сайта университета города Кампинас, которая содержит 4827 нормальных смс сообщений (ham) и 747 spam сообщений.
Я не делал никакой серьезной предобработки текста, типа стемминга, только несколько простых операций:
- уменьшил текст до строчных букв
- убрал все знаки пунктуации
- все числовые последовательности заменил единицей
Код предобработки
PreprocessSentence <- function(s)
{
# Cut and make some preprocessing with input sentence
words <- strsplit(gsub(pattern="[[:digit:]]+", replacement="1", x=tolower(s)), '[[:punct:][:blank:]]+')
return(words)
}
LoadData <- function(fileName = "./Data/Spam/SMSSpamCollection")
{
# Read data from text file and makes simple preprocessing:
# to lower case -> replace all digit strings with 1 -> split with punctuation and blank characters
con <- file(fileName,"rt")
lines <- readLines(con)
close(con)
df <- data.frame(lab = rep(NA, length(lines)), data = rep(NA, length(lines)))
for(i in 1:length(lines))
{
tmp <- unlist(strsplit(lines[i], '\t', fixed = T))
df$lab[i] <- tmp[1]
df$data[i] <- PreprocessSentence(tmp[2])
}
return(df)
}
Следующая функция создает разбиение массива данных в соответствующих пропорциях, генерируя тем самым индексы тренировочного, валидационного и тестового набора данных:
Сепарация дата сета
CreateDataSet <- function(dataSet, proportions = c(0.6, 0.2, 0.2))
{
# Creates a list with indices of train, validation and test sets
proportions <- proportions/sum(proportions)
hamIdx <- which(df$lab == "ham")
nham <- length(hamIdx)
spamIdx <- which(df$lab == "spam")
nspam <- length(spamIdx)
hamTrainIdx <- sample(hamIdx, floor(proportions[1]*nham))
hamIdx <- setdiff(hamIdx, hamTrainIdx)
spamTrainIdx <- sample(spamIdx, floor(proportions[1]*nspam))
spamIdx <- setdiff(spamIdx, spamTrainIdx)
hamValidationIdx <- sample(hamIdx, floor(proportions[2]*nham))
hamIdx <- setdiff(hamIdx, hamValidationIdx)
spamValidationIdx <- sample(spamIdx, floor(proportions[2]*nspam))
spamIdx <- setdiff(spamIdx, spamValidationIdx)
ds <- list(
train = sample(union(hamTrainIdx, spamTrainIdx)),
validation = sample(union(hamValidationIdx, spamValidationIdx)),
test = sample(union(hamIdx, spamIdx))
)
return(ds)
}
Затем создается модель на основании входного массива данных:
Создание модели
CreateModel <- function(data, laplaceFactor = 0)
{
# creates naive bayes spam classifier based on data
m <- list(laplaceFactor = laplaceFactor)
m[["total"]] <- length(data$lab)
m[["ham"]] <- list()
m[["spam"]] <- list()
m[["hamLabelCount"]] <- sum(data$lab == "ham")
m[["spamLabelCount"]] <- sum(data$lab == "spam")
m[["hamWordCount"]] <- 0
m[["spamWordCount"]] <- 0
uniqueWordSet <- c()
for(i in 1:length(data$lab))
{
sentence <- unlist(data$data[i])
uniqueWordSet <- union(uniqueWordSet, sentence)
for(j in 1:length(sentence))
{
if(data$lab[i] == "ham")
{
if(is.null(m$ham[[sentence[j]]]))
{
m$ham[[sentence[j]]] <- 1
}
else
{
m$ham[[sentence[j]]] <- m$ham[[sentence[j]]] + 1
}
m[["hamWordCount"]] <- m[["hamWordCount"]] + 1
}
else if(data$lab[i] == "spam")
{
if(is.null(m$spam[[sentence[j]]]))
{
m$spam[[sentence[j]]] <- 1
}
else
{
m$spam[[sentence[j]]] <- m$spam[[sentence[j]]] + 1
}
m[["spamWordCount"]] <- m[["spamWordCount"]] + 1
}
}
}
m[["uniqueWordCount"]] <- length(uniqueWordSet)
return(m)
}
Последняя функция, касающаяся модели, классифицирует входящее сообщение, используя обученную модель:
Классификация сообщения
ClassifySentense <- function(s, model, preprocess = T)
{
# calculate class of the input sentence based on the model
GetCount <- function(w, ls)
{
if(is.null(ls[[w]]))
{
return(0)
}
return(ls[[w]])
}
words <- unlist(s)
if(preprocess)
{
words <- unlist(PreprocessSentence(s))
}
ham <- log(model$hamLabelCount/(model$hamLabelCount + model$spamLabelCount))
spam <- log(model$spamLabelCount/(model$hamLabelCount + model$spamLabelCount))
for(i in 1:length(words))
{
ham <- ham + log((GetCount(words[i], model$ham) + model$laplaceFactor)
/(model$hamWordCount + model$laplaceFactor*model$uniqueWordCount))
spam <- spam + log((GetCount(words[i], model$spam) + model$laplaceFactor)
/(model$spamWordCount + model$laplaceFactor*model$uniqueWordCount))
}
if(ham >= spam)
{
return("ham")
}
return("spam")
}
Для тестирования модели на множестве используется следующая функция:
Тестирование модели
TestModel <- function(data, model)
{
# calculate percentage of errors
errors <- 0
for(i in 1:length(data$lab))
{
predictedLabel <- ClassifySentense(data$data[i], model, preprocess = F)
if(predictedLabel != data$lab[i])
{
errors <- errors + 1
}
}
return(errors/length(data$lab))
}
Для поиска оптимального коэффициента размытия используется кроссвалидация на соответствующем множестве:
Кроссвалидация модели
CrossValidation <- function(trainData, validationData, laplaceFactorValues, showLog = F)
{
cvErrors <- rep(NA, length(laplaceFactorValues))
for(i in 1:length(laplaceFactorValues))
{
model <- CreateModel(trainData, laplaceFactorValues[i])
cvErrors[i] <- TestModel(validationData, model)
if(showLog)
{
print(paste(laplaceFactorValues[i], ": error is ", cvErrors[i], sep=""))
}
}
return(cvErrors)
}
Следующий код считывает данные, создает модели для значений параметра размытия от 0 до 10, выбирает наилучший результат, тестирует модель на раннее не используемом тестовом множестве и затем строит график изменения ошибки на кроссвалидационном множестве от параметра размытия и финальный уровень ошибки на тестовом множестве:
rm(list = ls())
source("./Spam/spam.R")
set.seed(14880)
fileName <- "./Data/Spam/SMSSpamCollection"
df <- LoadData()
ds <- CreateDataSet(df, proportions = c(0.7, 0.2, 0.1))
laplaceFactorValues <- 1:10
cvErrors <- CrossValidation(df[ds$train, ], df[ds$validation, ], 0:10, showLog = T)
bestLaplaceFactor <- laplaceFactorValues[which(cvErrors == min(cvErrors))]
model <- CreateModel(data=df[ds$train, ], laplaceFactor=bestLaplaceFactor)
testResult <- TestModel(df[ds$test, ], model)
plot(cvErrors, type="l", col="blue", xlab="Laplace Factor", ylab="Error Value", ylim=c(0, max(cvErrors)))
title("Cross validation and test error value")
abline(h=testResult, col="red")
legend(bestLaplaceFactor, max(cvErrors), c("cross validation values", "test value level"), cex=0.8, col=c("blue", "red"), lty=1)
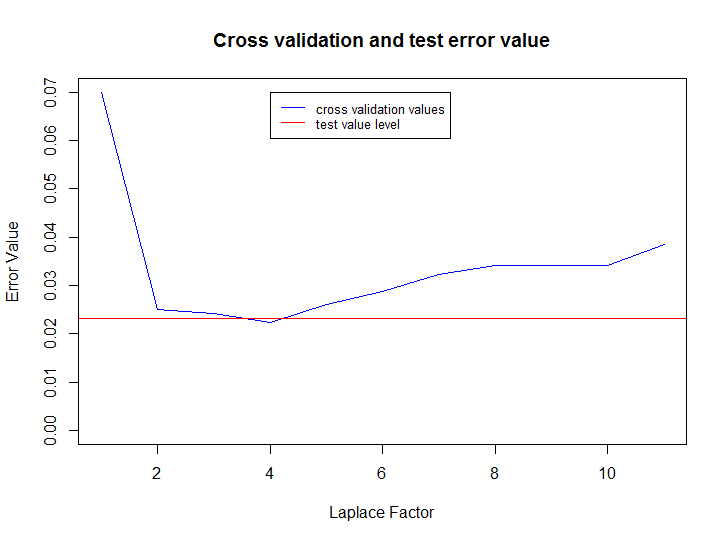
Весь код можно скачать с гитхаба.
Заключение
Как видите, этот метод очень эффективен даже при простой предобработке, показатель ошибки на тестовом множестве (отношение неверно классифицированных сообщений к общему количеству сообщений) всего 2.32%. Где вы можете использовать этот метод? Например, на вашем сайте есть множество комментариев, вы недавно ввели рейтинг комментариев от 1 до 5, и у вас только малая часть реально с рейтингом расставленным людьми; тогда вы можете автоматически расставить более-менее релевантные рейтинги на оставшиеся комментарии.