Введение
Одной из задач обучения без учителя является задача нахождения топологической структуры, которая наиболее точно отражает топологию распределения входных данных. Существует несколько подходов решения этой задачи. Например, алгоритм Самоорганизующихся Карт Кохонена является методом проецирования многомерного пространства в пространство с более низкой размерностью (как правило, двумерное) с предопределенной структурой. В связи с понижением размерности исходной задачи, и предопределенной структурой сети, возникают дефекты проецирование, анализ которых является сложной задачей. В качестве одной из альтернатив данному подходу, сочетание конкурентного обучения Хебба и нейронного газа является более эффективным в построении топологической структуры. Но практическому применению данного подхода препятствует ряд проблем: необходимы априорные знания о необходимом размере сети и сложность применения методов адаптации скорости обучения к данной сети, излишняя адаптация приводит к снижению эффективности при обучении новым данным, а слишком медленная скорость адаптации вызывает высокую чувствительность к зашумленным данным.
Для задач онлайн обучения или длительного обучения, перечисленные выше методы не подходят. Фундаментальная проблема для таких задач — это как система может приспособиться к новой информации без повреждения или уничтожения уже известной.
В данной статье рассматривается алгоритм SOINN, который частично решает озвученные выше проблемы.
Обзор рассматриваемого алгоритма
В задаче обучения без учителя, нам необходимо разделить поступающие данные на классы, без предварительных знаний о их количестве. Также необходимо определить топологию исходных данных.
Итак, алгоритм должен удовлетворять следующим требованиям:
- Обучение в режиме онлайн, или lifetime
- Разделение на классы без предварительных знаний о входных данных
- Разделение данных с нечеткой границей и выявление основной структуры кластеров
SOINN представляет собой нейронную сеть с двумя слоями. Первый слой используется для определения топологической структуры кластеров, а второй для определения числа кластеров и выявления узлов-прототипов для них. Сначала обучается первый слой сети, а затем, используя данные полученные при обучении первого слоя, обучается второй слой сети.
Для задачи классификации без учителя, необходимо определить, принадлежит ли входной образ одному из ранее полученных кластеров или представляет новый. Предположим, что два образа принадлежат одному кластеру, если расстояние(по заранее заданной метрике) между ними меньше порога расстояния T. Если T будет слишком большим, то все входные образы будут отнесены к одному кластеру. Если T слишком маленький, то каждый образ будет изолирован как отдельный кластер. Для получения разумного разбиения на кластеры, T должно быть больше, чем внутриклассовое расстояние и меньше межклассового.
Для каждого из слоев сети SOINN мы должны вычислить порог T. Первый слой не имеет априорных знаний о структуре исходных данных, поэтому T подбирается адаптивно, основываясь на знаниях структуры уже построенной сети и текущего входного образа. При обучении второго слоя, мы можем посчитать внутриклассовое и межклассовое расстояние и подобрать константное значение порога T.
Для представления топологической структуры, в онлайн или lifetime задачах обучения, рост сети является важным элементом для снижения ошибки и адаптации к меняющимся условиям, сохраняя старые данные. Но в то же время, неконтролируемое увеличение числа узлов приводит к перегрузке сети и «переобучению» её в целом. Поэтому необходимо решать, когда и как добавлять новые узлы в сеть, а когда предотвратить добавление новых узлов.
Для добавления узлов, SOINN использует схему, при которой вставка происходит в регионе с максимальной ошибкой. А для оценки полезности вставки, используется «радиус ошибки» являющийся оценкой полезности вставки. Эта оценка гарантирует, что вставка приведет к уменьшению ошибки и контролирует прирост узлов, и в конце концов стабилизирует их количество.
Для составления связей между нейронами используется конкурентное правило Хебба, предложенное Мартинесом в сетях пределения топологий (TRN). Конкурентное правило Хебба может быть описано так: для каждого входного сигнала, объединяются два ближайших узла. Доказано, что каждый граф оптимально представляет топологию входных данных. В онлайн или lifetime задачах обучения, узлы изменяют свое местоположение медленно, но постоянно. Таким образом, узлы, которые являются соседними на ранней стадии, возможно, не являются близкими в более поздней стадии. Тем самым появляется необходимость удаления соединений, которые в последнее время не обновляются.
В общем случае происходит также перекрытие существующих кластеров. Чтобы определить количество кластеров точно, предполагается, что входные данные являются разделяемыми: плотности вероятности в центральной части каждого кластера выше, чем плотность в части между кластерами, а также перекрытие кластеров имеет низкую плотность вероятности. Разделение кластеров происходит путем удаления узлов из регионов с низкой плотностью вероятности. Алгоритм SOINN предлагает следующую стратегию для удаления узлов из регионов с низкой плотностью вероятности: если число сигналов, генерируемых до сих пор является целым кратным заданному параметру, то удалить те узлы, которые имеют только одного топологического соседа, или не имеют соседей вовсе и если локальный накопленный уровень сигнала является маленьким, то считаем такие узлы лежащими в области низкой плотности вероятности и удаляем их.
Описание алгоритма
Теперь, на основе вышесказанного, мы можем дать формальное описание алгоритма обучения для сети SOINN. Этот алгоритм используется для обучение и первого и второго слоев сети. Разница состоит только в том, что входные данные для обучения второго слоя порождаются первым слоем и при обучении второго слоя, мы имеем знания о топологической структуре первого слоя, для вычисления постоянного порога подобия.
Используемые обозначения
- A — множество, используемое для хранения узлов
- NA — число узлов в множестве A
- C — множество связей между узлами
- NC — число ребер в C
- Wi — n-мерный вектор весов для узла i
- Ei — локальный аккумулятор ошибки для узла i
- Mi — локальный аккумулятор сигнала для узла i
- Ri — радиус ошибки для узла i. Ri = Ei / Mi
- Ci — метка кластера для узла i
- Q — число кластеров
- Ti — порог подобия для узла i
- Ni — набор топологических соседей для узла i
- age(i,j) — возраст связи между узлами i и j
Алгоритм
- Инициализировать множество узлов A двумя узлами, c1 и c2:
A = {c1, c2}
Инициализировать множество ребер C пустым множеством:
C = {}. - Подать на вход новый сигнал x из R^n.
- Найти в множестве A узлы победителя s1 и второго победителя, как узлы с ближайшим и следующим за ним векторами весов(по некоторой заданной метрике). Если расстояние между x, s1 и s2 больше порогов подобия Ts1 или Ts2, то создать новый узел и перейти на шаг 2.
- Если ребро между s1 и s2 не существует, то создать его. Установить возраст ребра между ними равным 0.
- Увеличить возраст всех дуг, выходящих из s1 на 1.
- Прибавить расстояние между входным сигналом и победителем к локальной суммарной ошибке Es1.
- Увеличить локальное количество сигналов узла s1:
Ms1 = Ms1 +1 - Адаптировать вектора весов победителя и его прямых топологических соседей:
Ws1 = Ws1 + e1(t)(x — Ws1)
Wsi = Wsi + e2(t)(x — Wsi)
Где e1(t) и e2(t) — коэффициенты обучения победителя и его соседей. - Удалить ребра с возрастом, выше заданного порогового значения.
- Если число генерируемых до сих пор входных сигналов кратно параметру lambda, вставить новый узел и удалить узлы в областях низкой плотности вероятности по следующим правилам:
- Найти узел q с максимальной ошибкой.
- Найти среди соседей q узел f с максимальной ошибкой.
- Добавить узел r таким образом, чтобы его весовой вектор был средним арифметическим весовых коэффициентов q и f.
- Рассчитать накопленную ошибку Er, суммарное количество сигналов Mr, и наследованный радиус ошибки:
Er = alpha1 * (Eq + Ef)
Mr = alpha2 * (Mq + Mf)
Rr = alpha3 * (Rq + Rf) - Уменьшить суммарную ошибку узлов q и r:
Eq = beta * Eq
Ef = beta * Ef - Уменьшить накопленное количество сигналов:
Mq = gamma * Mq
Mf = gamma * Mf - Определить, успешно ли прошла вставка нового узла. Если вставка не может уменьшить среднюю погрешность данной области, то вставка не удалась. Добавленная вершина удаляется, а все параметры возвращаются в исходные состояния. Иначе обновляем радиус ошибки всех задействованных во вставке узлов:
Rq = Eq / Mq
Rf = Ef / Mf
Rr = Er / Mr. - Если вставка прошла успешно, создать связи q<->r и r<->f и удалить связь q<->f.
- Среди всех узлов в A найти такие, которые имеют только одного соседа, затем сравнить накопленное количество входных сигналов со средним значением всех узлов. Если узел содержит всего одного соседа и счетчик сигналов не превышает адаптивного порога, удалить его из набора узлов. Например, если Li = 1 и Mi < c * sum_{j = 1...Na} Mj / Na (где 0 < c < 1), тогда удалить вершину i.
- Удалить все изолированные узлы.
- По прошествии долгого времени LT каждому классу из входных данных будет соответствовать компонента связанности в построенном графе. Обновить метки классов.
- Перейти к пункту 2 и продолжить обучение.
Алгоритм вычисления порогового значения T
Для первого слоя порог подобия T вычисляется адаптивно по следующему алгоритму:
- Инициализировать порог подобия для новых узлов равным +oo.
- Когда узел является первым или вторым победителем, обновить значение порога подобия:
- Если узел имеет прямых топологических соседей (Li > 0), обновить значение Ti как максимальное расстояние между узлом и его соседями:
Ti = max || Wi — Wj || - Если узел не имеет соседей, Ti устанавливается как минимальное расстояние между узлом и другими узлами в множестве A:
Ti = min || Wi — Wc ||
- Если узел имеет прямых топологических соседей (Li > 0), обновить значение Ti как максимальное расстояние между узлом и его соседями:
Для второго слоя порог подобия постоянный и вычисляется следующим образом:
- Вычислить внутриклассовое расстояние:
dw = 1 / Nc * sum_{(i,j) in C} || Wi — Wj || - Вычислить межклассовые расстояния. Расстояние между классами Ci и Cj вычисляется следующим образом:
db(Ci, Cj) = max_{i in Ci, j in Cj} || Wi — Wj || - В качестве порога подобия Tc взять минимальное межклассовое расстояние, которое превышает внутриклассовое расстояние.
Принципиальная схема работы алгоритма
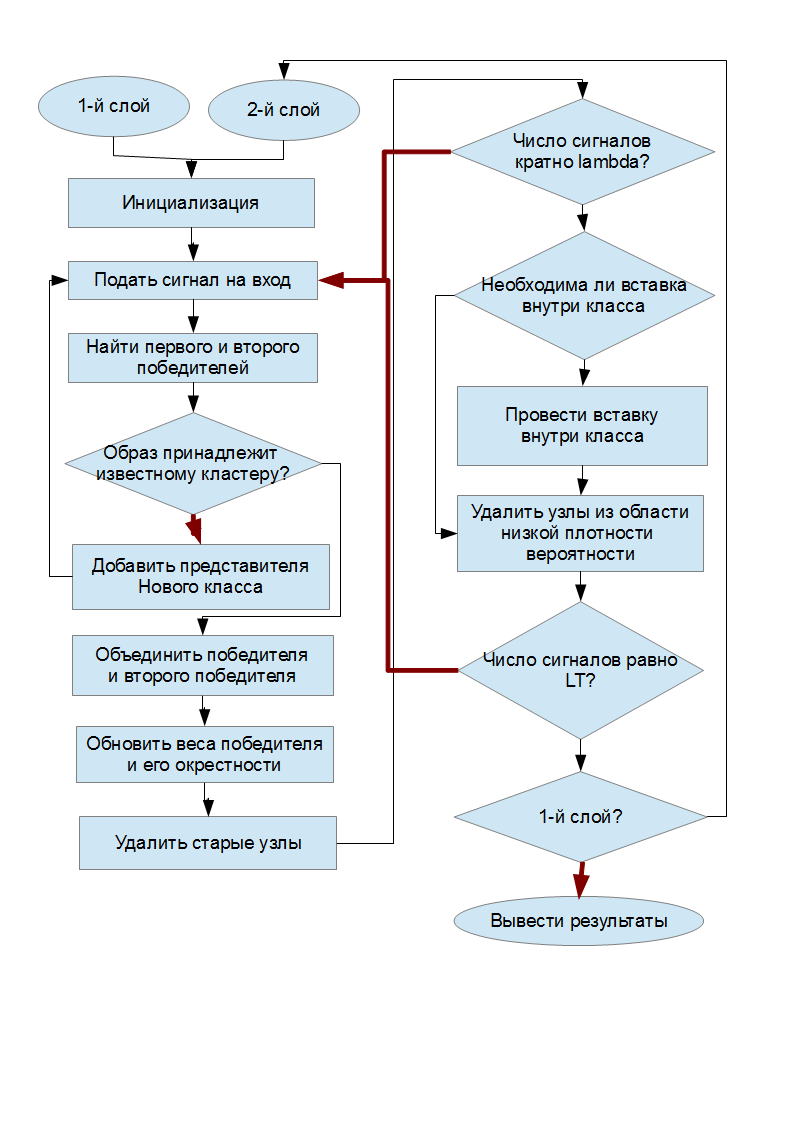
В «условных» ромбах черные стрелки соответствуют выполнению условия, а красные невыполнению.
Эксперименты
Для проведения экспериментов с рассматриваемым алгоритмом, он был реализован на языке C++ с применением библиотеки Boost Graph Library. Код можно скачать здесь.
Для проведения экспериментов, были выбраны следующие параметры алгоритма:
- lambda = 100
- age_max = 100
- c = 1.0
- alpha1 = 0.16
- alpha2 = 0.25
- alpha3 = 0.25
- beta = 0.67
- gamma = 0.75
В качестве тестовых данных было использовано следующее изображение, представляющее два класса(кольцо и круг)

После подачи на вход сети SOINN 20000 случайно взятых точек из этих классов, был сформирован первый слой сети, следующего вида

На основе данных, полученных на первом слое, был сформирован второй слой следующего вида

Выводы
В данной статье мы рассмотрели один из алгоритмов обучения без учителя, основанный на топологизации данных. Из результатов полученных экспериментальным путем можно сделать вывод о справедливости применения данного метода.
Но все-же стоит отметить недостатки алгоритма SOINN:
- Поскольку слои сети обучаются последовательно друг за другом, то сложно определить момент, когда стоит остановить обучение первого слоя и приступить к обучению второго слоя.
- При изменениях первого слоя сети, необходимо полностью переобучать второй слой. В связи с этим не решена проблема онлайн обучения.
- В сети есть много параметров, которые необходимо подбирать вручную.
Использованная литература
«An incremental network for on-line unsupervised classification and topology learning» Sgen Furao, Osamu Hasegawa, 2005