Существуют три вида лжи: ложь, наглая ложь и статистика (источник)
Есть такой замечательный жанр — "вредные советы", в котором детям дают советы, а дети, как известно, всё делают наоборот и получается всё как раз правильно. Может быть и со всем остальным так получится?
Статистика, инфографика, big data, анализ данных и data science — этим сейчас кто только не занят. Все знают как правильно всем этим заниматься, осталось только кому-то написать как НЕ нужно этого делать. В данной статье мы именно этим и займемся.
Hazen Robert "Curve fitting". 1978, Science.
Структура статьи:
- Введение
- Предвзятая выборка (Sampling bias)
- Правильно выбираем среднее (Well-chosen average)
- И еще 10 неудачных экспериментов, про которые мы не написали
- Играем со шкалой
- Выбираем 100%
- Скрываем нужные числа
- Визуальная метафора
- Пример качественной визуализации
- Заключение и дальнейшее чтение
Предвзятая выборка (Sampling bias)
В 1948 году во время президентской гонки в США в ночь на оглашение результатов выборов Труман (демократы) против Дьюи (республиканцы) газета Chicago Tribune опубликовала свой, пожалуй, самый знаменитый заголовок DEWEY DEFEATS TRUMAN (см. фото). Сразу после закрытия участков газета провела опрос, обзвонив огромное (достаточное для выборки) число избирателей, и всё предвещало оглушительную победу Дьюи. На фото мы видим смеющегося Трумана, победителя выборов 48го года. Что же пошло не так?

Людей обзванивали действительно случайно и в достаточном количестве, но в 48-ом году телефон был доступен только людям определенного достатка и редко встречался у людей с небольшим заработком. Таким образом, сам метод опроса вносит поправку в распределение голосов. Выборка не учитывала достаточно широкий пласт избирателей Трумана (как правило демократы имеют большую долю голосов среди бедного населения), которым телефон в свою очередь был недоступен. Такая выборка и называется предвзятой (sampling bias).
Народное творчество о данном феномене:
По данным интернет-голосования 100% людей пользуются интернетом.
Зарплата выпускников
Никого не удивляло, что когда мы слышим о зарплатах выпускников ВУЗов, то почему-то всегда это неправдоподобно высокие цифры? В США сейчас доходит дело даже до судов, где выпускники утверждают, что данные по зарплатам искусственно завышены.

(картинка из How to Lie with Statistics)
Это довольно старая проблема, согласно Darrell Huff, подобный вопрос возникал у выпускников Yale 24-го года. И на самом деле все говорят правду, да только не всю. Сбор статистики происходил в виде опросов (а в те годы с помощью бумажной почты). Отправляют ответ далеко не все, а только небольшая часть всех выпускников; активнее других отвечают те, у кого дела идут хорошо (что часто выражается в неплохой зарплате), поэтому мы видим только «хорошую» часть картины. Это-то и создаёт предвзятость выборки и делает результаты подобных опросов абсолютно бесполезными.
Правильно выбираем среднее (Well-chosen average)
Представим себе компанию, в которой руководитель получает 25 тысяч, его заместитель 7,6 тысяч, топ-менеджеры по 5,5 тысяч, менеджеры среднего звена по 3,5 тысячи, младшие менеджеры по 2,5 тысячи, а обычные работники по 1,4 тысячи (абстрактных фунтиков) в месяц.
И наша задача представить информацию о компании в положительном свете. Мы можем написать средняя заработная плата в компании составляет X, но что означает среднее? Рассмотрим возможные варианты (см. схему ниже):

(картинка из How to Lie with Statistics)
Арифметическое среднее некоторого конечного множества X={xi} — это такое число m равное mean(X) из уравнения:
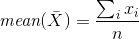
Это самая бесполезная информация с точки зрения работника — 3,472 средняя зарплата, но за счет чего получается такая высокая цифра? За счет высоких зарплат руководства, что создает иллюзию, что работник будет получать столько же. С точки зрения работника данная величина не является особо информативной.
Конечно же народное творчество не обошло стороной эту особенность «средней величины» в виде средне арифметического
Чиновники едят мясо, я — капусту. В среднем мы едим голубцы.
Медиана некоторого распределения P(X) (X={xi}), это такая величина m, что она удовлетворяет следующему уравнению:
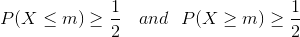
Проще говоря, половина работников получает больше данной величины, а половина меньше — ровно середина распределения! Данная статистика достаточно информативна для работников компании, так как она позволяет определить как зарплата сотрудника соотносится с большинством сотрудников.
Мода конечного множества X={xi}, это число m, которое встречается в X чаще всего. В данном случае, мода может быть наиболее информативна для человека, который собирается начать работать в данной компании.
Таким образом в зависимости от ситуации под средним значением может пониматься любая из указанных выше величин (в принципе и не только из них). Поэтому принципиально важно понять, как же рассчитывается это среднее значение.
И еще 10 неудачных экспериментов, про которые мы не написали
Опустим обычную газету в серную кислоту, а журнал ТВ Парк — в дистиллированную воду! Почувствовали разницу? С журналом ничего не произошло — бумага как новая! (Весь ролик тут.)

Наши исследования сообщают, что зубная паста Doake's на 23% процента эффектнее конкурентов, и всё это благодаря Dr Cornish's Tooth Powder! (Который наверняка содержал β-каротин и секретную формулу леса — прим. автора.) Вы наверное удивитесь, но исследование действительно провели и даже выпустили технический отчет. И эксперимент действительно показал, что зубная паста на 23% процента эффективнее конкурентов (чтобы это не значило). Но только вся ли это история?
В действительности выборка для эксперимента составляла всего лишь дюжину человек (согласно Darrell Huff и уже упомянутой книге). Это именно та выборка, которая нужна, чтобы получить любые результаты! Представим, что мы подбрасываем монетку пять раз. Какова вероятность, что все пять раз выпадет орел? (1/2)5 = 1/32. Всего лишь одна тридцать вторая, это не может быть просто совпадением, если выпадут все пять орлов, ведь так? А теперь представим, что мы повторяем этот эксперимент 50 раз. Хоть одна из этих попыток увенчается успехом. О ней-то мы и напишем в отчете, а все другие эксперименты никуда не пойдут. Таким образом мы получим исключительно случайные данные, которые отлично вписываются в нашу задачу.
Играем со шкалой
Предположим, завтра нужно показать на совещании, что мы догнали конкурентов, но числа немного не сходятся, что же делать? Давайте немного подвигаем шкалой! Даже известный своей качественной работой с данными New York Times выпустил подобный совершенно сбивающий с толку график (обратите внимание на скачок с 800к до 1,5м в центре шкалы).
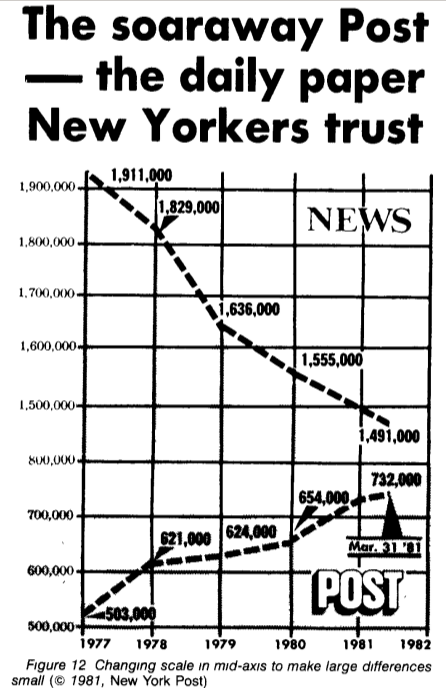
(пример из How to Display Data Badly Howard Wainer. The American Statistician, 1984.)
Выбираем 100%
Представим, что в прошлом году молоко стоило 10 копеек за литр и хлеб был 10 копеек за буханку. В этом году молоко упало в цене на 5 копеек, а хлеб вырос на 20. Внимание вопрос, что мы хотим доказать?
Представим, что прошлый год — это 100%, основание для расчетов. Тогда молоко упало в цене на 50% процентов, а хлеб вырос на 200%, среднее 125%, а значит в целом цены выросли на 25%.
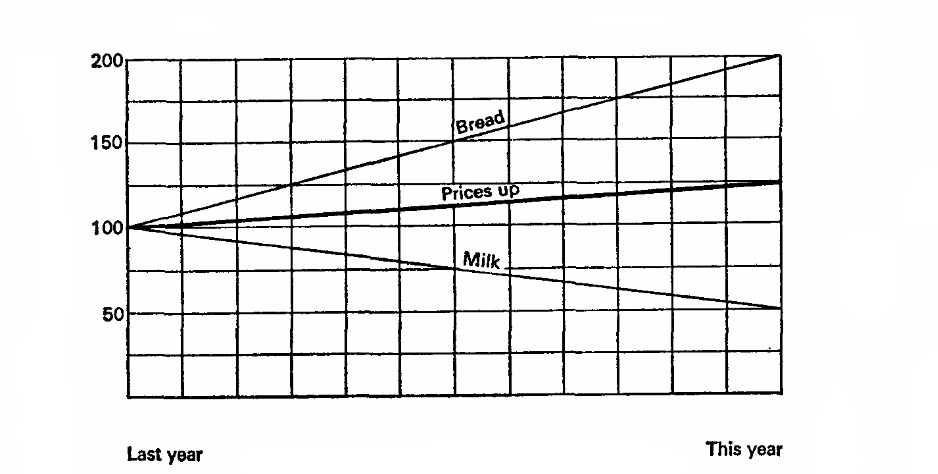
Давайте попробуем еще разок, пусть текущий год — 100%, значит цены на молоко составляли 200% в прошлом году, а хлеб 50%. А значит, в прошлом году цены в среднем были на 25% выше!
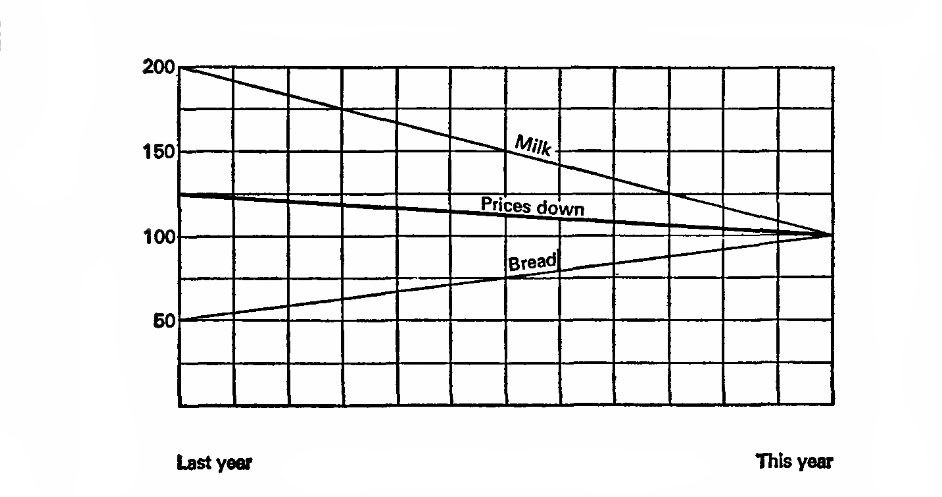
(графики и пример из главы «How to Statisticulate» How to Lie with Statistics)
Скрываем нужные числа
Лучший способ что-то скрыть — это отвлечь внимание. Например, рассмотрим зависимость количества частных и публичных школ (в тысячах штук) по годам. Из графика видно, что число публичных школ сокращается, а число частных существенно не изменяется.
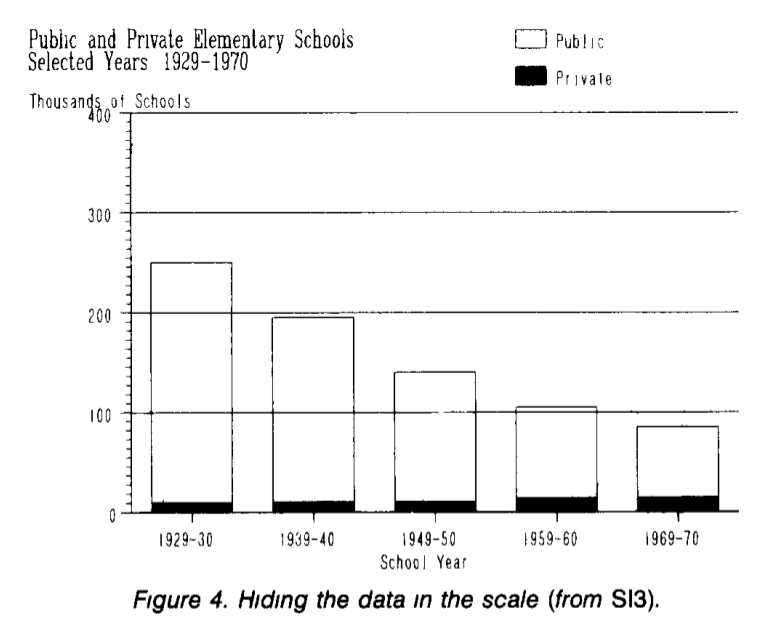
На самом деле рост числа частных школ скрыт на фоне числа публичных школ. Так как они отличаются на порядок, то фактически любые изменения будут не заметны на шкале с достаточно большим шагом. Перерисуем число частных школ отдельно; теперь мы отчетливо видим существенный рост числа частных школ, который был «скрыт» на предыдущем графике.
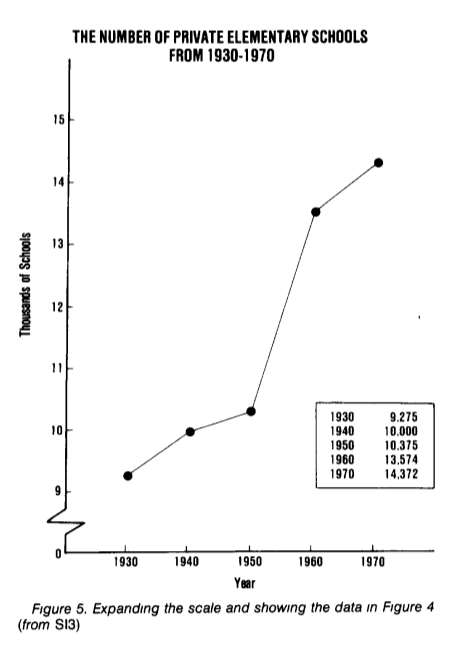
(пример и графики из How to Display Data Badly, Howard Wainer. The American Statistician, 1984.)
Визуальная метафора
Если сравнивать не с чем, а запутать очень хочется, то самое время для непонятных визуальных метафор. Например, если мы изобразим вместо длины площадь на графике, то любой рост будет казаться гораздо более значительным.
Рассмотрим потребление количества пива в США за 1970-1978 годы в миллионах баррелей и долю рынка компании Schlitz (см. график ниже). Неплохо выглядит, внушительно. Не правда ли?

А теперь давайте избавимся от ненужного «мусора» на данном графике и перерисуем его в нормальном виде. Уже как-то не так внушительно и серьезно выходит.
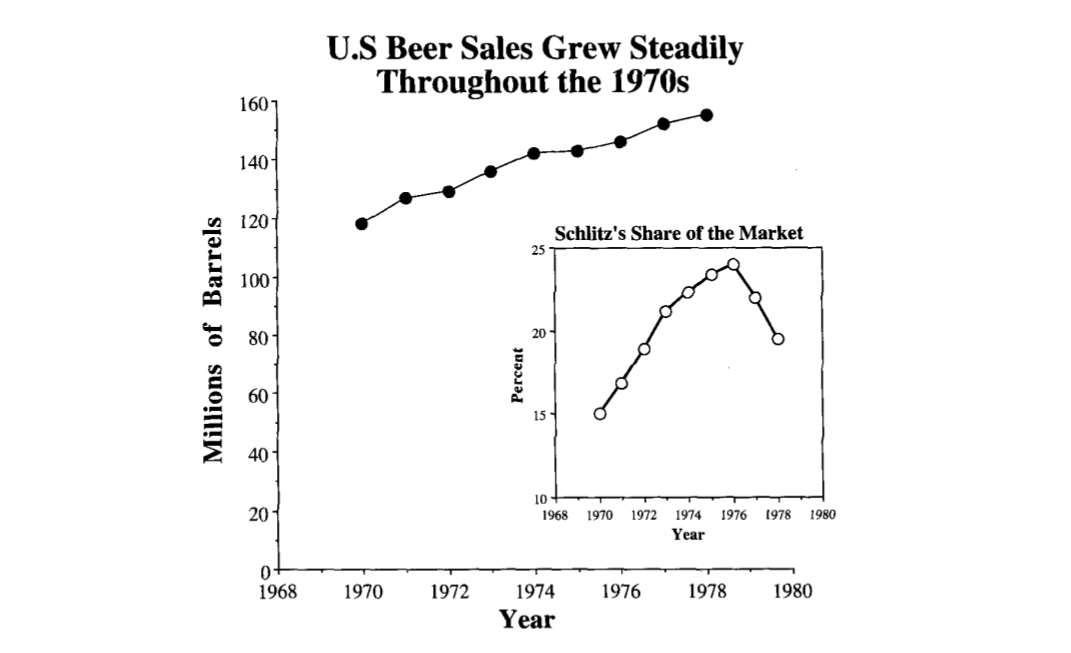
(графики и примеры из John P. Boyd, lecture notes How to Graph Badly or What. NOT to Do)
Первая картинка не врет, все числа в ней верные, только она неявно преподносит данные в совершенно ином свете.

(картинка из How to Lie with Statistics).
Пример качественной визуализации
Качественная визуализация прежде всего преподносит результаты, избегая неоднозначности, и передает достаточное количество информации в сжатом объеме. Про работу Шарль-Жозефа Минара хорошо сказано тут:
Тут прекрасно совершенно все, зрителя не держат за идиота, и не тратят его время на втыкание вcensored. Широкая бежевая полоса показывает размер армии в каждой точке похода. В правом верхнем углу — Москва, куда приходит французская армия и откуда начинается отступление, показанное черной полосой. К маршруту отступления для дополнительного интереса привязан график времени и температуры.
Вывод в итоге: изумленный зритель сравнивает размер армии на старте с тем, что вернулось домой. Зритель весь в чувствах, он узнал новое, он ощутил масштаб, он заворожен, он понял, что в школе ничего не узнал.

(Charles Joseph Minard: Napoleon's Retreat From Moscow (The Russian Campaign 1812-1813), 1869.)
Заключение и дальнейшее чтение
76% всей статистики взято из головы
Данная подборка покрывает далеко не полный список приемов, которые осознанно, а также не осознанно искажают данные. Данная статья прежде всего демонстрирует, что мы должны очень внимательно следить за предоставленными нам статистическими данными и выводами сделанными на их основе.
Короткий список к дальнейшему чтению:
How to Lie with Statistics — замечательная небольшая книга, невероятно интересно и хорошо написанная, читается на одном дыхании. Демонстрирует основные «ошибки», которые допускают СМИ (и не только они) при работе с данными.
How to Display Data Badly. Howard Wainer. The American Statistician (1984) — сборник типичных ошибок и общих «вредных» правил, чаще всего встречающихся в работах с визуализацией данных.
