
Многие пробовали играть во Flappy Bird. Редко кому удается пролететь за 50 труб, очень немногие долетают до сотни-двух. Некоторые пробовали создать бота, в том числе на хабре. Удивительно, но даже у самого успешного бота, которого можно найти на просторах интернета, результаты не очень-то впечатляют – что-то около 160 очков. Возникает вопрос, а можно ли вообще играть во Flappy Bird бесконечно долго? Или всегда с некоторой, пусть и небольшой, вероятностью может встретиться последовательность препятствий, которую даже опытный игрок/идеальный бот не сможет преодолеть?
И тут на помощь приходит математика. Давайте найдем выигрышную стратегию для Flappy Bird.
Модель
Опишем математическую модель игры. Наше игровое поле — плоскость. Есть птичка — квадрат со сторонами длины w, параллельными координатным осям. Есть препятствия — трубы — вертикальные полосы ширины wtube с горизонтальными проемами высоты hgap. Расстояние между двумя соседними препятствиями по горизонтали фиксировано и равно Δtube. Расположение горизонтального проема для каждой трубы случайно (равномерно в некотором диапазоне). Кроме того есть пол — горизонтальная прямая f. Пол — это тоже препятствие. Картинка:
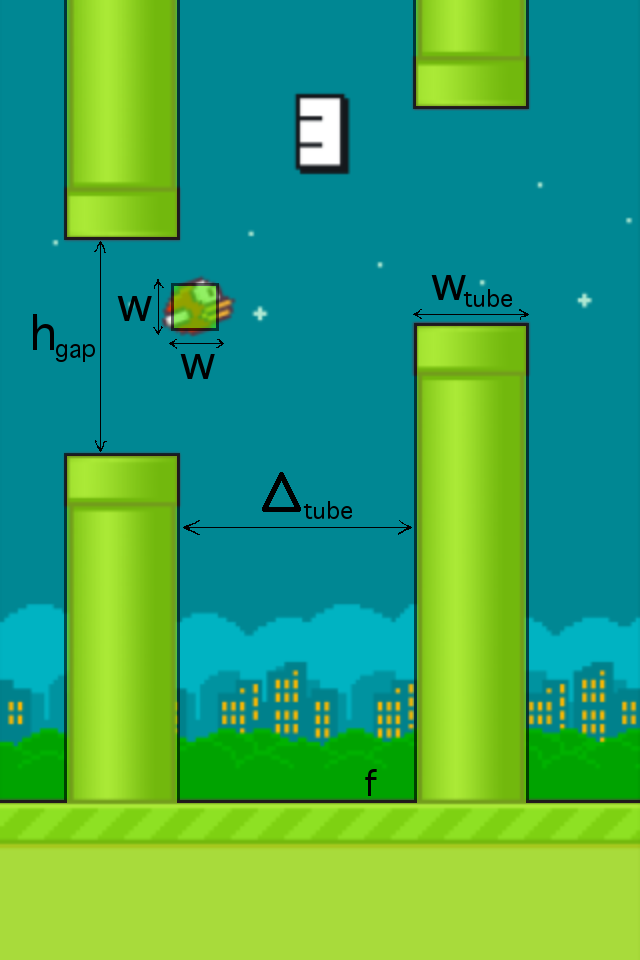
Скорость птички по горизонтали постоянна и равна vx. На птичку также действует гравитация, придавая ей вертикальное ускорение g. Изначально скорость птички по вертикали равна 0. В каждый момент времени игрок может сделать тап, то есть сделать так, чтобы вертикальная скорость птички стала равна vjump. Кроме того, на птичку действует некое подобие сопротивления воздуха – ее вертикальная скорость ограничена снизу константой vfall. Фактически, это означает, что после каждого тапа птичка движется по параболе, переходящей в какой-то момент в прямую. Траекторию, по которой двигается птичка после тапа, будем называть падаболой (парабола падения). Выглядит это так:
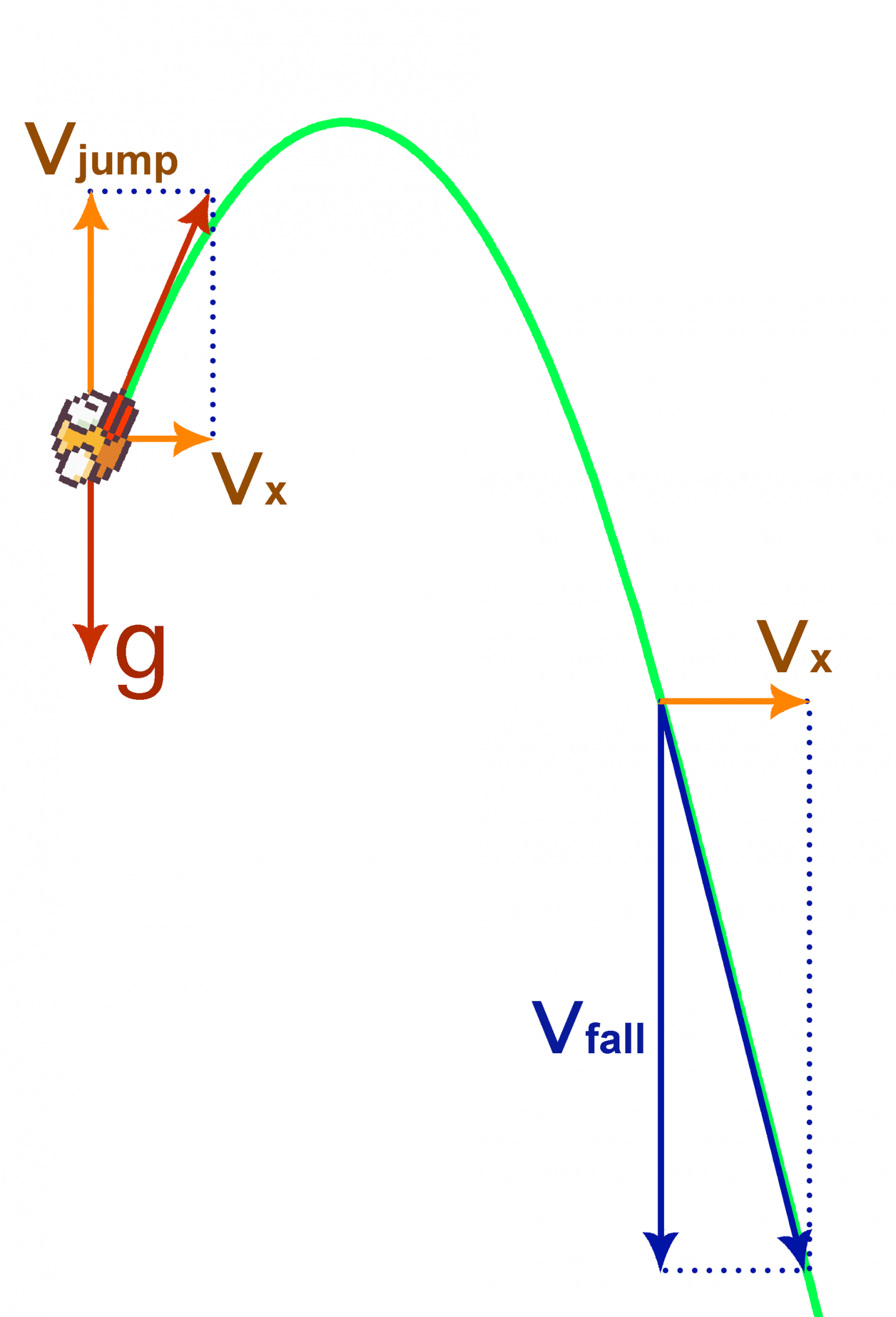
Игра заканчивается, когда птичка касается препятствия. Задачей игрока является максимизация пройденного расстояния.
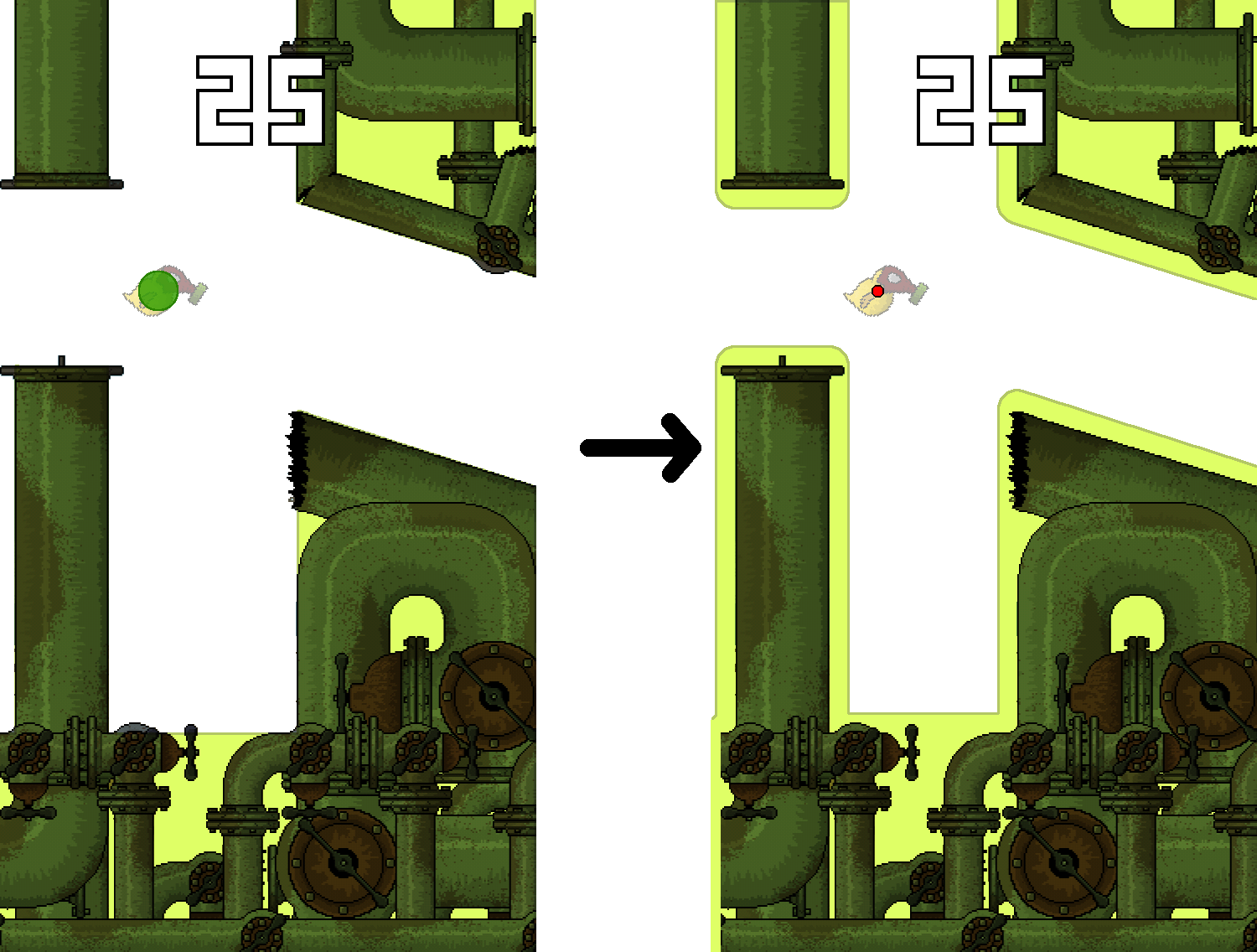
Прежде чем переходить собственно к стратегии прохождения сделаем один фокус. Анализировать пересечения квадратной птички с препятствиями не очень-то удобно. Но, оказывается, легко перейти к эквивалентной модели, в которой птичка является точкой. Для этого достаточно «сдуть» птичку до размера точки (центра исходного квадрата), одновременно «раздувая» препятствия. При этом исходный квадрат пересекается с препятствиями тогда и только тогда, когда новая точечная птичка лежит в раздутом препятствии. Картинка:

По-научному результат «раздутия» препятствий называется суммой Минковского.
Сумма Минковского
Википедия сообщает:
Суммой Минковского двух подмножеств A и B линейного пространства V называется множество C, состоящее из сумм всевозможных векторов из A и B: C={c|c=a+b,a∈A,b∈B}
С бытовой точки зрения можно считать, что сумма Минковского фигур A и B есть фигура, получаемая, если к каждой точке B приложить фигуру A – см. правый рисунок.
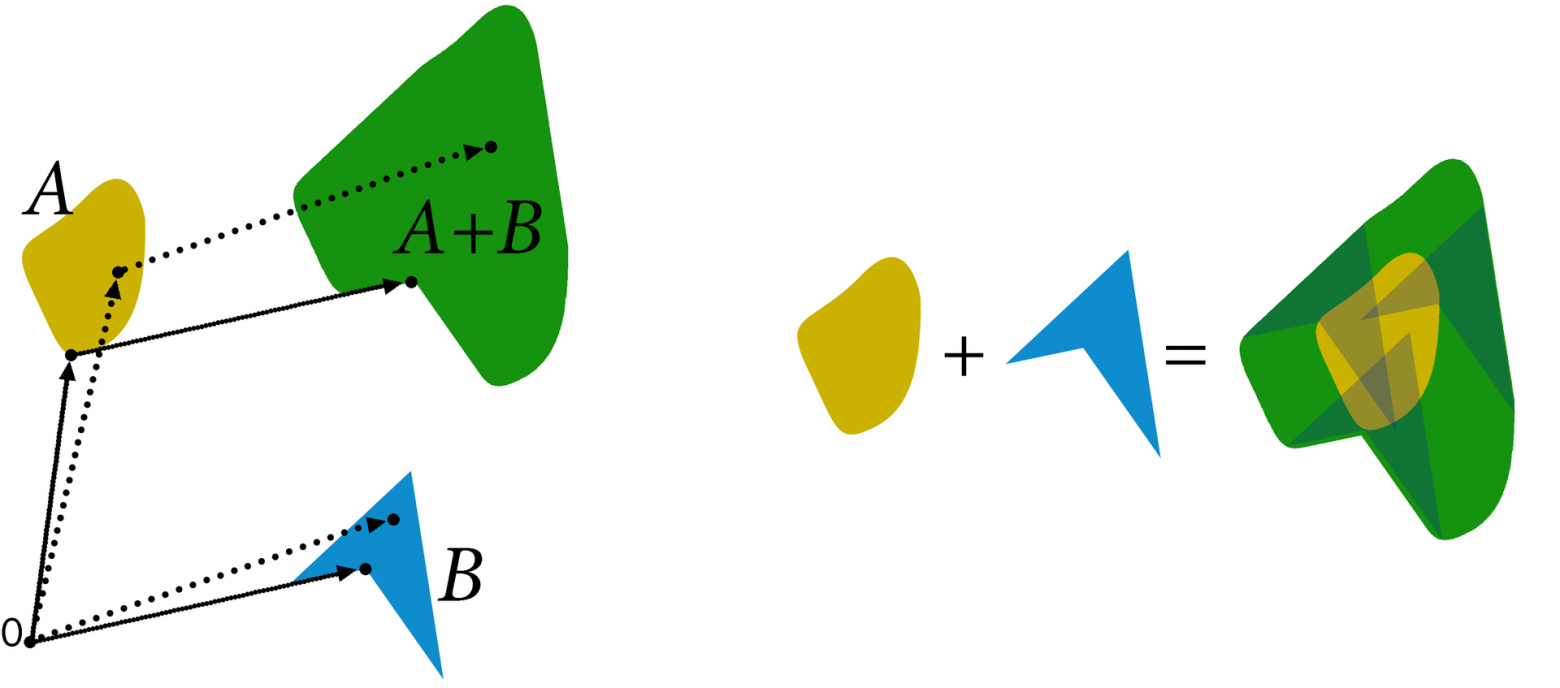
Обратная падабола
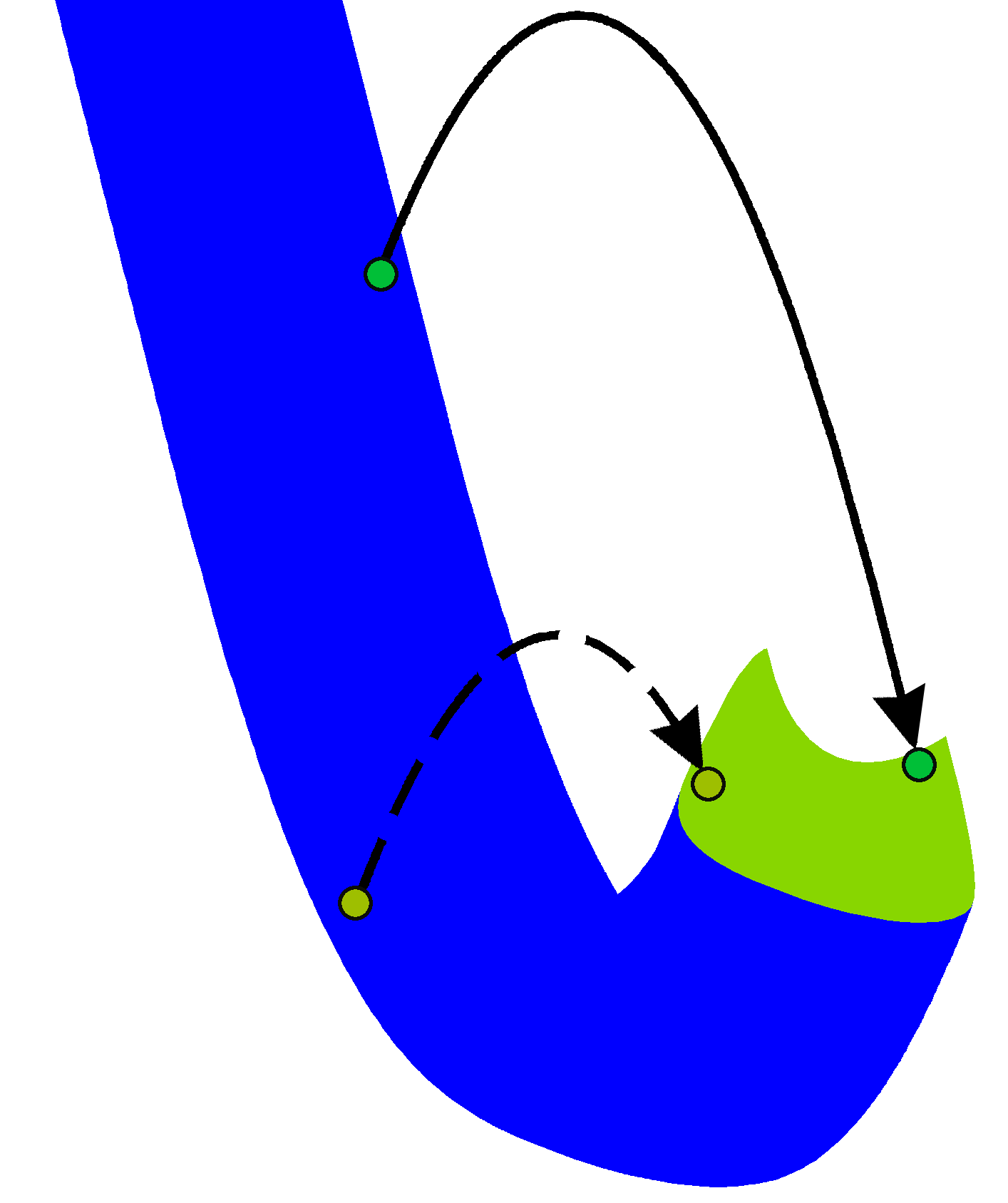
Решим вспомогательную задачу: где должна находиться птичка, чтобы после тапа она пролетела через заданную точку A? Точнее говоря, требуется найти геометрическое место точек, таких что падаболы, проведенные из них, проходят через фиксированную точку A. См. средний рисунок. Пусть v⃗ – произвольный вектор, соединяющий начало падаболы с одной из ее точек. Легко видеть, что после тапа в точке A-v⃗ птичка пролетит через точку A. То есть A-v⃗ принадлежит искомому геометрическому месту точек. Более того, взяв всевозможные вектора v⃗, мы получим все искомые точки. Но чем является множество точек вида A-v⃗, где v есть радиус вектор до одной из точек падаболы? Это путь, центрально-симметричный падаболе после отражения относительно точки A. С картинкой, кстати, понятнее:
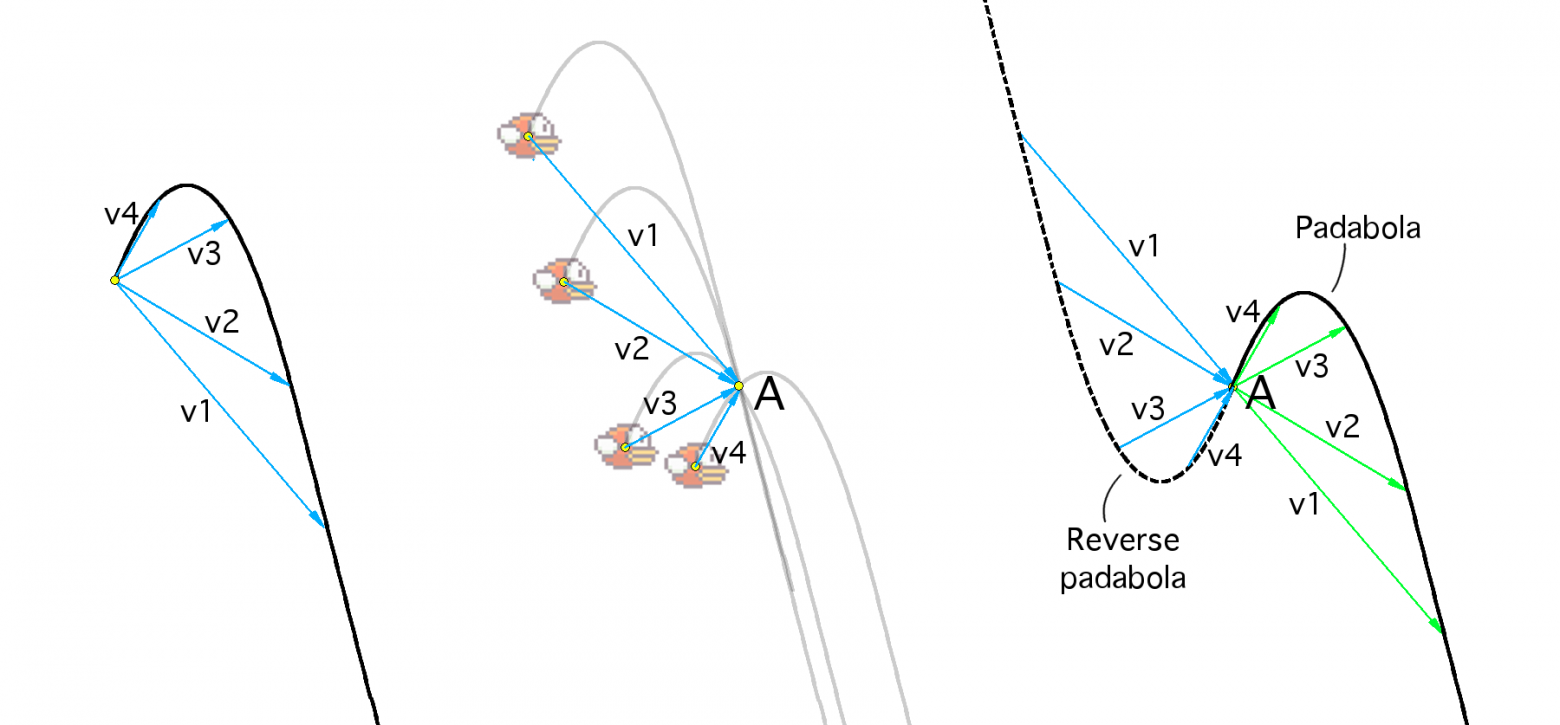
Можно обобщить задачу: где нужно тапнуть, чтобы пролететь через заданную область S? Исходя из всего вышесказанного ответом является сумма Минковского области S и обратной падаболы:
Верхние препятствия
Перейдем, наконец, к основной задаче – нахождению выигрышной стратегии. Только сначала решим ее в упрощенном случае. Пусть в модели отсутствуют нижние половинки труб и пол. То есть у нас имеются только верхние части препятствий. Рассмотрим отдельно стоящую верхнюю половину трубы. Пусть птичка начала свой путь где-то далеко слева от этого препятствия. Допустим, в какой-то момент времени птичка врезалась в трубу. Как мы знаем по предыдущему параграфу, это означает, что был совершен тап в области, получающейся путем прибавления к препятствию обратной падаболы. Раскрасим получившуюся область синим цветом. Рисунок:
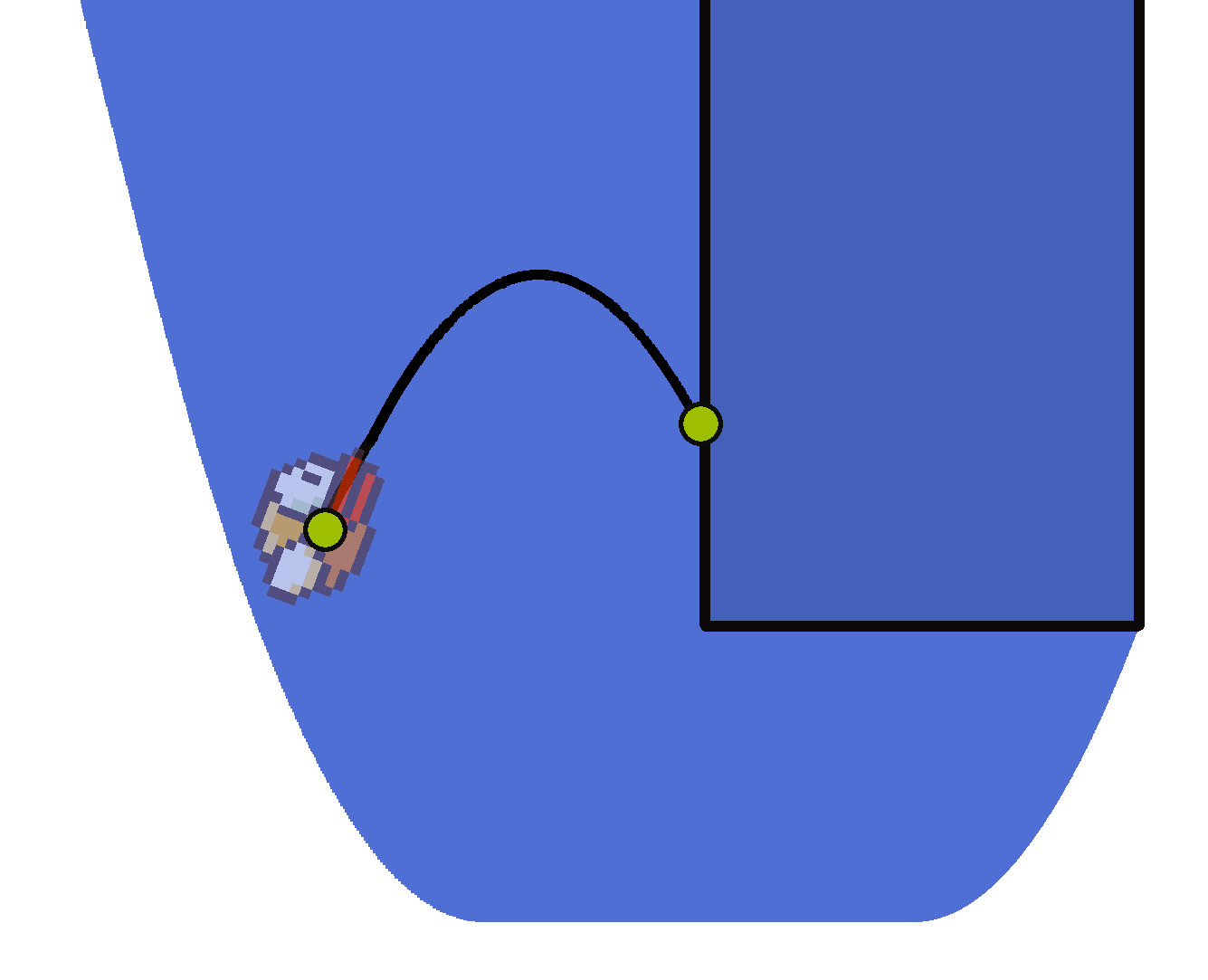
Заметим, что если игрок тапнул в какой-либо точке синей области, то соответствующая падабола сначала пересекается с препятствием и только потом покидает синюю область. Другими словами игрок будет вынужден либо проиграть, либо еще раз тапнуть в синей области. Ну а поскольку отдельно взятая синяя область ограничена справа, лететь в ней до бесконечности не получится, и, в конце-концов, птичка умрет. Таким образом, тап в синей области всегда приводит к поражению. Более того, тапы вне синей области не могут привести к проигрышу – без тапа в синей области нельзя врезаться в верхнее препятствие, а больше нечему помешать птичке лететь.
В результате, для случая одних только верхних препятствий получаем следующее утверждение.
Утверждение. Если птичка начала свой полет вне объединения синих областей, то бесконечные выигрышные стратегии существуют. И все выигрышные стратегии описываются следующим образом: вне синих областей игрок может принимать произвольные решения, в синих областях игрок не может тапать.
Нижние препятствия
Теперь рассмотрим случай, когда в модели присутствуют только нижние половинки труб. То есть нет верхних половинок и пола. Опять же рассмотрим отдельно стоящее нижнее препятствие. Проведем через его верхний левый угол (точку A) луч AC, угол наклона которого составляет atan(vjump/vx) — то есть луч, направленный вдоль скорости птички в момент сразу после тапа. Пусть птичка оказалась ниже луча AC. Тогда независимо от действий игрока она не сможет подниматься с вертикальной скоростью большей чем vjump. С учетом постоянной горизонтальной скорости vx это приводит к неминуемому столкновению с препятствием, то есть проигрышу. Раскрасим нижнее препятствие и область ниже луча AC в красный цвет. Вот такие красные горки получаются:
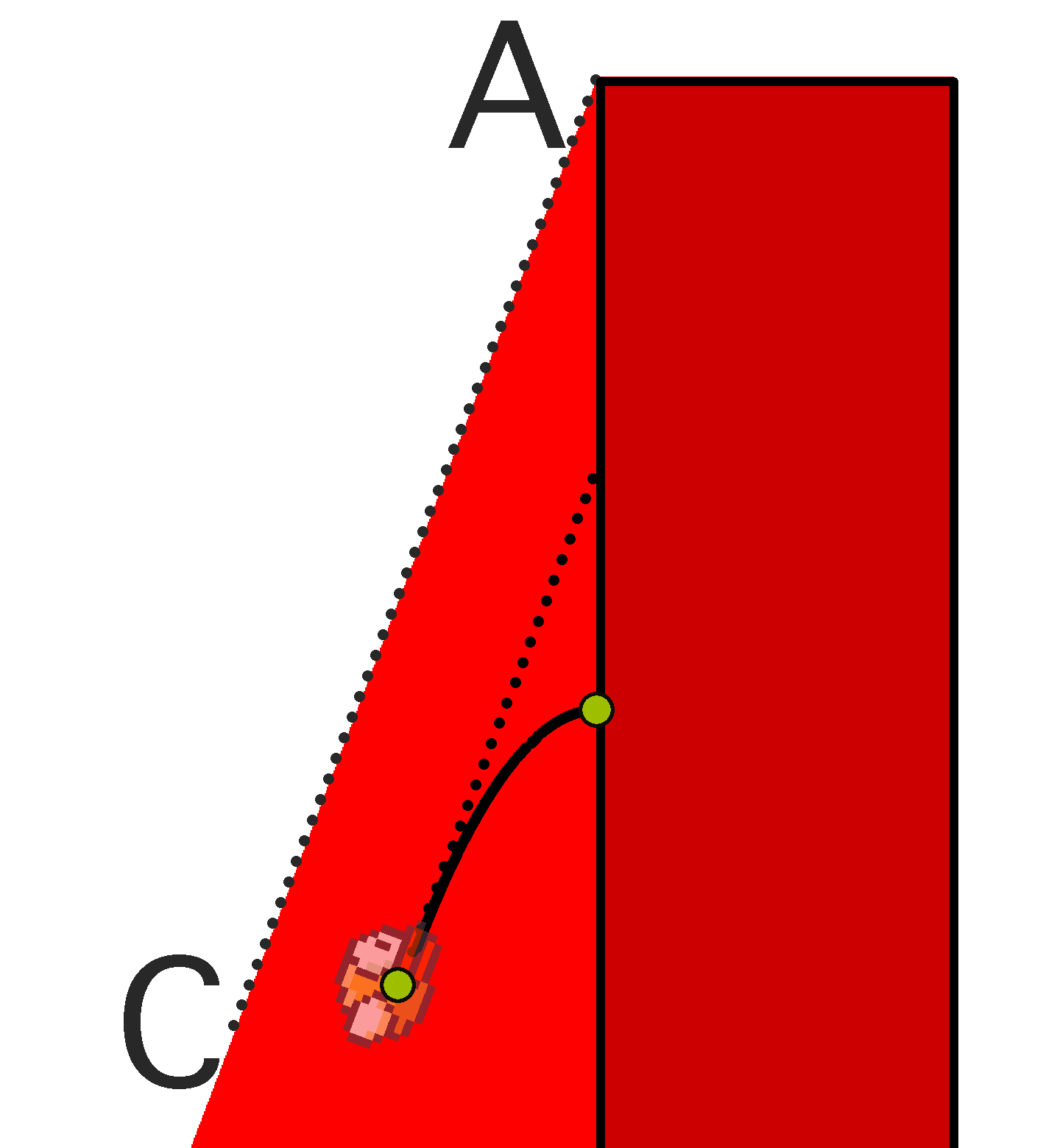
Получается, что при любой выигрышной стратегии птичка не должна попадать в красные области. Более того, если птичка находится вне красной области в некоторый момент времени, то она сможет оставаться вне нее сколь угодно долго. Действительно, всегда при приближении к границе красной области игрок может начинать тапать достаточно часто, чтобы не оказаться в ней.
Добавим пол. Несложно видеть, что пол можно воспринимать как еще одну красную область в форме нижней полуплоскости.
Таким образом, если присутствуют только нижние препятствия и пол, то верно:
Утверждение. Если птичка в начальный момент времени находится вне объединения красных областей, то существуют бесконечные выигрышные стратегии. Все выигрышные стратегии можно сформулировать так: вне красной области игрок может принимать любые решения, при приближении к красной области игрок должен тапать.
Все препятствия вместе
Рассмотрим общую ситуацию. Пусть есть и верхние половинки труб, и нижние, и пол. Вполне понятно следующее:
Утверждение. Если объединение синих областей не пересекается с объединением красных и птичка изначально находится вне синих и красных областей, то существуют выигрышные стратегии. Любая выигрышная стратегия описывается так: вне синих и красных областей можно принимать любые решения, в синих областях тапать нельзя, при приближении к красным областям необходимо тапать.
Отсутствие пересечений синих и красных областей для существования такой стратегии существенно. Действительно, может так получиться, что птичка пролетая через синюю область вплотную приблизится к границе красной – в этом случае если игрок тапнет, то проиграет, если не тапнет, тоже проиграет.
Возникает вопрос, а пересекаются ли синие и красные области в реальной игре? Оказывается, иногда пересекаются. И происходит это ровно в одном случае: когда возникает достаточно большой перепад высот вниз между проемами двух соседних труб.
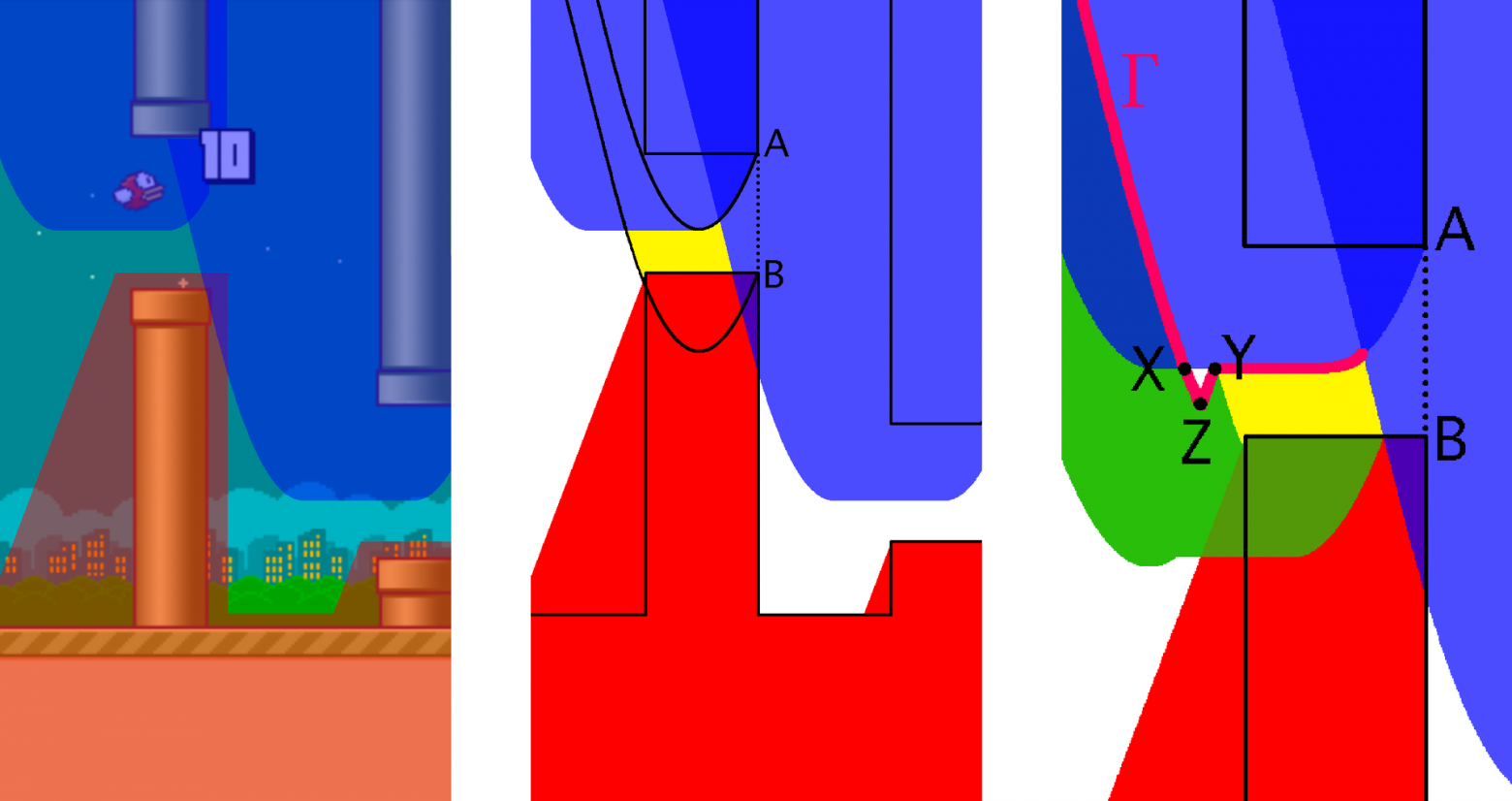
Проанализируем данную ситуацию. Пусть птичка сумела пролететь через эти трубы. Значит, в какой-то момент времени она пересекла отрезок AB. Но это значит, что был совершен тап в области между обратными падаболами, проведенными из точек A и B. В то же время данный тап не мог быть произведен ни в синей области, ни в красной. Остается только область, изображенная на рисунке желтым цветом.
То есть для существования выигрышной стратегии нужно уметь гарантировать попадание в желтую область. Дальше останется только сделать тап и опасный участок будет преодолен. Для того, чтобы понять, всегда ли мы сможем попасть в желтую область, сложим ее с обратной падаболой – получим область (на рисунке зеленая), в которую достаточно попасть, чтобы за один тап долететь до желтой. Заметим, что если в какой-то момент времени будет совершен тап в точке, лежащей выше линии Г, в желтую область мы уже попасть не сможем. И наоборот, для любой точки ниже этой границы мы всегда можем, тапнув достаточное число раз подряд, подняться в зеленую область, дальше, тапнув один раз, попасть в желтую и, соответственно, преодолеть препятствие. Другими словами, точки, находящиеся выше линии Г в нашей терминологии стоит покрасить в синий цвет. Правда, по большей части они и так уже синие, за исключением криволинейного треугольника XYZ. Докрасим XYZ в синий. Теперь для формулировки выигрышной стратегии осталось добавить фразу: если птичка оказалась в желтой области, необходимо хоть раз тапнуть до того, как птичка эту область покинет.
Заметим, что дораскрашивание треугольничка в синий цвет не могло добавить пересечений красных и синих областей, а потому не повлияло на анализ проходимости игры в целом.
В итоге, в общем случае получаем:
Утверждение. Пусть птичка в начальный момент времени находится вне синих и красных областей. Тогда существуют бесконечные выигрышные стратегии. Все такие стратегии можно описать так: вне синих и красных областей можно тапать в любой момент времени; в синих областях тапать нельзя; при приближении к красным необходимо тапать; попав в желтую область, нужно тапнуть хоть один раз до выхода из нее.
Интересно, что стратегия вида начать полет выше некоторой линии и тапать, как только птичка до нее опускается (например, в качестве такой линии логично было бы взять верхнюю границу красных областей, немного сдвинутую вверх) выигрышной видимо не будет ни для какой линии.
Практика
Все это хорошо, но хотелось бы немного практических результатов. Хардварных ботов на хабре уже видели, так что мы решили сделать софтверный. Совершенно случайно под рукой оказался код нашего клона под названием Tappinator, физическая модель которого достаточно близка к оригинальной игре – старались, замеряли. У нас, правда, птичка круглая (хотя, может, она и во Flappy Bird круглая, но разница невелика, а с квадратной объяснять проще) и есть дополнительные препятствия – наклонные. Вот так «раздуваются» препятствия для круглой птички:
В результате синие и красные области у нас такие:

Что касается желтых областей, они все также возникают для стандартных труб, но кроме того возникают в случае наклонных препятствий, направленных снизу вверх (со своими криволинейными синими треугольниками и вообще):

Ну и, собственно, видео с ботами:
На видео можно увидеть как 50 птичек вполне успешно долетают до 1000, как выглядят всякие цветные области с точки зрения бота и как бы выглядела игра, если бы одновременно летело 1000 птичек. В незакрашенных областях боты ведут себя случайным образом: у каждого из них своя фиксированная вероятность принять решение о прыжке в каждый момент времени. Можно заметить, что с точки зрения бота цветные области несколько больше, чем с точки зрения математики. Дело в том, что бот имеет возможность принимать решение только 60 раз в секунду, да и физическая модель обновляется тоже дискретно.
Вывод
Вот так, оказывается даже в такой простой игре как Flappy Bird есть где развернуть математическую теорию. Причем в действительности самое интересное с этого момента только начинается. Дальше возникает вопрос, как быть с препятствиями произвольной формы – тут приходится вводить такие понятия как фиолетовая тень, бордовая граница, право-линейно-связная область, право-линейно-связное замыкание и т.д. Также интересно, какой реакцией должен обладать человек (то есть какова допустимая ошибка по времени при тапе у него должна быть), чтобы он смог играть до бесконечности. Между прочим, это крайне нетривиальный вопрос, строгий ответ на который нам до сих пор не известен.