Мне давно не давало покоя желание рассчитать какой-нибудь достаточно сложный механизм и воплотить его жизнь.
Выбор пал на задачу об обратном маятнике. Итог на видео:
Я не буду приводить вывод уравнений движения, все таки это третий курс института. Для тех же, кому интересен вывод, в конце статьи ссылка, где он описан подробнее.
Систему представим в следующем виде:
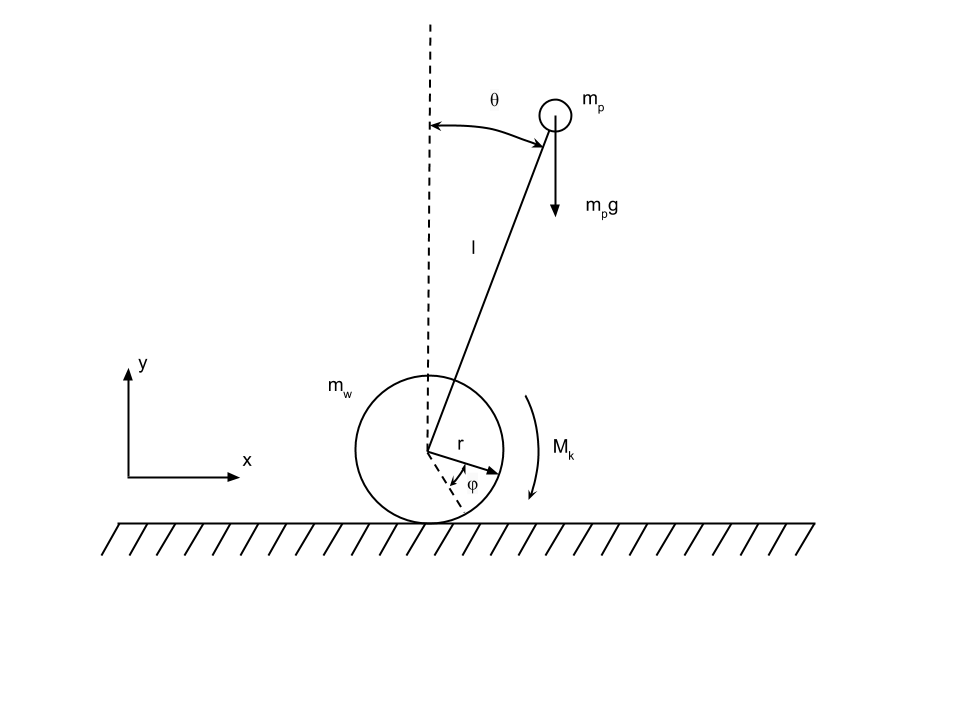
Маятник это масса mp прикрепленная на конце невесомого стержня длины l. На другой конец стержня прикреплен двигатель, развивающий максимальный момент Mk и передающий его на колесо массой mw и радиусом r.
Задача управления — стабилизировать маятник в вертикальном положении и возвращать в начальное положение колесо.
Уравнения движения, описывающие обратный маятник, представимы в следующем виде:
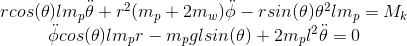
Они кажутся довольно неприятными, но сам робот о них ничего не знает, а управление использует линеаризованную модель, то есть такую:
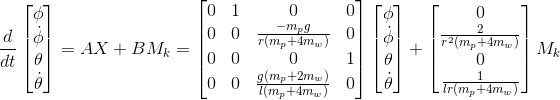
Завидую людям, у которых работает PID-регулятор. Я потратил несколько часов на подгонку его коэффициентов, но так и не сумел добиться стоящего результата. Научный руководитель посоветовал воспользоваться линейно-квадратичным регулятором(вики). Этот регулятор, в отличие от PID-регулятора, представляет собой просто произведение своих коэффициентов на ошибки по каждой координате. Никаких дискретных аналогов производной и интеграла. Однако для его вычисления нужна модель системы и умение решать уравнение Риккати, ну или Matlab.
В матлабе расчет регулятора представляет собой такой набор команд:
Здесь матрицы A и B — соответствующие матрицы из линеаризованной модели с подставленными значениями реального робота.
Матрица Q определяет на сколько нужно штрафовать систему за отклонение от начала координат, заметьте, в нашем случае в координаты входят скорости.
Матрица R определяет на сколько нужно штрафовать систему за растрату энергии управлением.
В переменной K будут лежать коэффициенты регулятора.
В Matlab simulink можно легко эмулировать систему, если кому-нибудь необходимо ссылка на репозитарий с математической моделью в конце статьи. Здесь же я только приведу графики.
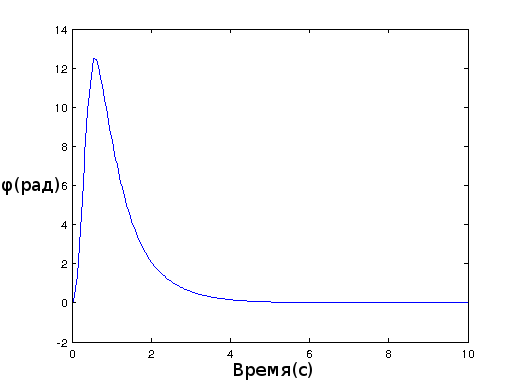
Угол отклонения маятника:
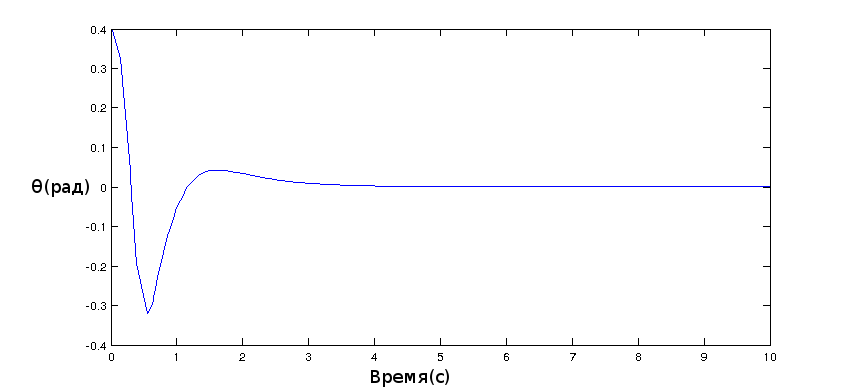
Угол отклонения колеса:
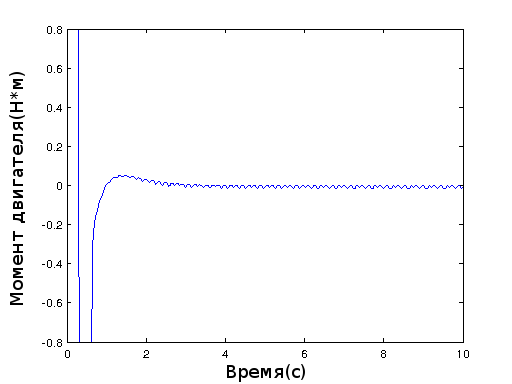
Момент двигателя:
Сам каркас робота это алюминиевые профиля 12мм и 14мм, они входят друг в друга. Соединены заклепками. Электроника прикреплена на кусок стеклотекстолита в форме буквы T. Моторы так же прикреплены через стеклотекстолитовый переходник.

Изначально я пытался использовать такие моторы:

Их крутящий момент 2,2кг*см или 0.2Нм. Исходя из симуляции нам нужно гораздо больше, поэтому были выбраны другие моторы:

ссылка на производителя
Максимальный крутящий момент 14кг*см или 1.4Нм. Тока они потребляют до 5A, поэтому популярный у ардуинщиков L293D тут не подойдет.
Для определения угла и угловой скорости используется IMU — гироскоп и акселерометр. У меня завалялась плата с гироскопом L3G и акселерометром с магнетометром LSM303. Подобных плат очень много и я не стану приводить код получения значений сенсоров. Однако показания датчиков нужно отфильтровать, так как гироскоп постоянно уходит, а акселерометр шумит и сильно врет, если робот начинает двигаться не меняя угла.
Используют разные фильтры, но наиболее популярны фильтр Калмана и RC-фильтр (complementary filter). Я использую такой код:
Работает не идеально, но достаточно хорошо для данной задачи.
Следующий сенсор — квадратурный энкодер на моторе. Он генерирует прямоугольные импульсы на 2х своих выводах:

Считать их можно либо прерываниями, либо считыванием значений в цикле. На arduino playground есть замечательная статья с примерами кода.
Осталось получить угловую скорость колеса. Тут на помощь приходит школьная формула пройденное расстояние/затраченное время.
ToPhiRad переводит количество тиков энкодера в угол колеса, мой энкодер выдает около 2240 тиков на оборот. Чтобы получить угол нужно умножить тики на 2 Пи и разделить на их количество при полном обороте колеса.
Показания сенсоров поступают в LQR регулятор:
Коэффициенты взяты из Matlab, правда для большей стабильности я подправил 2 первых коэффициента.
Мой драйвер, вернее его библиотека, принимает значения от -400 до 400. Я предположил, что на 400 он выдает на мотор 12В, т.е. мотор развивает максимальный момент (1.4Нм). Разделив 400 на 1.4 получаем коэффициент перевода из Нм, которые выдает LQR, в значения, понятные драйверу.
Просто стабилизировать робота в одной точке не очень интересно, поэтому к нему добавился BT-модуль HC-05. Модуль подключается к серийному порту микроконтроллера. Он работает на 3.3В, а arduino на 5В, поэтому подключать принимающий вход модуля надо через делитель напряжения. Вот схема подключения:

Во время цикла микроконтроллер опрашивает модуль на предмет символов:
В конечном итоге показания сенсоров поступают в регулятор, а его управление и воздействие пользователя поступают на моторы:
Раз в 50 миллисекунд посылается телеметрия-угол робота:
Управлять будем с телефона под android.
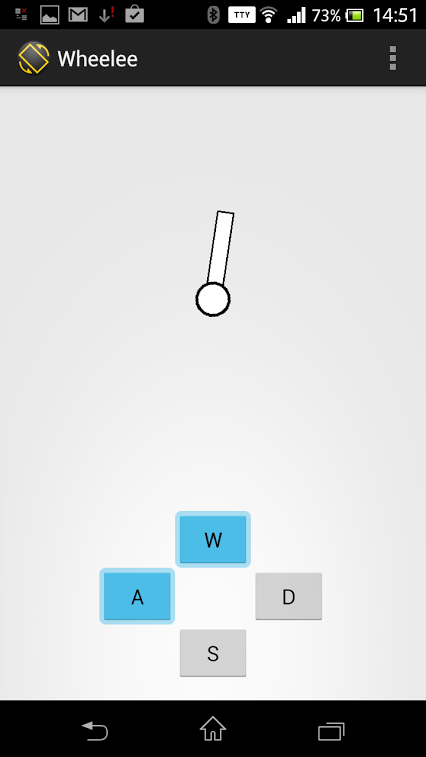
При запуске приложения попросим пользователя выбрать к кому подключаться, bt-модуль должен быть уже сопряжен с телефоном (стандартный код 1234).
После выбора устройства подключимся к нему:
После подключения стартует поток, который занимается коммуникацией между приложением и роботом:
Поток посылает сообщение основному потоку приложения через Handler, который определяется так:
balancerView это потомок класса SurfaceView, он занимается выводом на экран текущего положения робота.
Вот его метод перерисовки:
Команды роботу посылаются при появлении событий onTouch, чтобы можно было управлять роботом удерживая кнопку.
Самое приятное во всей постройке это то, что математическая модель сошлась с физической реализацией. Сама постройка железки не представляет из себя какой-то сложности, однако подбор правильных моторов, высоты робота, массы груза сверху и синтезирование управления довольно интересная задача.
Как и обещал вывод уравнений движения перевернутого маятника на колесе: Вывод уравнений и немного о постройке
репозитарий на GitHub
Выбор пал на задачу об обратном маятнике. Итог на видео:
Математическая модель
Я не буду приводить вывод уравнений движения, все таки это третий курс института. Для тех же, кому интересен вывод, в конце статьи ссылка, где он описан подробнее.
Систему представим в следующем виде:

Маятник это масса mp прикрепленная на конце невесомого стержня длины l. На другой конец стержня прикреплен двигатель, развивающий максимальный момент Mk и передающий его на колесо массой mw и радиусом r.
Задача управления — стабилизировать маятник в вертикальном положении и возвращать в начальное положение колесо.
Уравнения движения, описывающие обратный маятник, представимы в следующем виде:
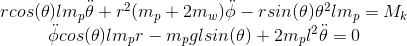
Они кажутся довольно неприятными, но сам робот о них ничего не знает, а управление использует линеаризованную модель, то есть такую:
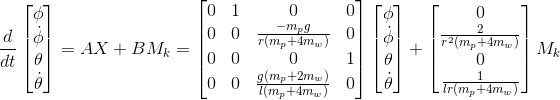
Синтезирование управления
Завидую людям, у которых работает PID-регулятор. Я потратил несколько часов на подгонку его коэффициентов, но так и не сумел добиться стоящего результата. Научный руководитель посоветовал воспользоваться линейно-квадратичным регулятором(вики). Этот регулятор, в отличие от PID-регулятора, представляет собой просто произведение своих коэффициентов на ошибки по каждой координате. Никаких дискретных аналогов производной и интеграла. Однако для его вычисления нужна модель системы и умение решать уравнение Риккати, ну или Matlab.
В матлабе расчет регулятора представляет собой такой набор команд:
A=[0 1.0 0 0;0 0 -140 0;0 0 0 1.0;0 0 28 0]
B=[0;212.85;0;-19.15]
Q=[5 0 0 0;0 5 0 0;0 0 1 0;0 0 0 1]
R=1500
[K,S,e]=lqr(A,B,Q,R)
Здесь матрицы A и B — соответствующие матрицы из линеаризованной модели с подставленными значениями реального робота.
Матрица Q определяет на сколько нужно штрафовать систему за отклонение от начала координат, заметьте, в нашем случае в координаты входят скорости.
Матрица R определяет на сколько нужно штрафовать систему за растрату энергии управлением.
В переменной K будут лежать коэффициенты регулятора.
Симуляция
В Matlab simulink можно легко эмулировать систему, если кому-нибудь необходимо ссылка на репозитарий с математической моделью в конце статьи. Здесь же я только приведу графики.
Угол отклонения маятника:

Угол отклонения колеса:

Момент двигателя:

Реализация в железе
Сам каркас робота это алюминиевые профиля 12мм и 14мм, они входят друг в друга. Соединены заклепками. Электроника прикреплена на кусок стеклотекстолита в форме буквы T. Моторы так же прикреплены через стеклотекстолитовый переходник.

Изначально я пытался использовать такие моторы:

Их крутящий момент 2,2кг*см или 0.2Нм. Исходя из симуляции нам нужно гораздо больше, поэтому были выбраны другие моторы:

ссылка на производителя
Максимальный крутящий момент 14кг*см или 1.4Нм. Тока они потребляют до 5A, поэтому популярный у ардуинщиков L293D тут не подойдет.
Для определения угла и угловой скорости используется IMU — гироскоп и акселерометр. У меня завалялась плата с гироскопом L3G и акселерометром с магнетометром LSM303. Подобных плат очень много и я не стану приводить код получения значений сенсоров. Однако показания датчиков нужно отфильтровать, так как гироскоп постоянно уходит, а акселерометр шумит и сильно врет, если робот начинает двигаться не меняя угла.
Используют разные фильтры, но наиболее популярны фильтр Калмана и RC-фильтр (complementary filter). Я использую такой код:
float lastCompTime=0;
float filterAngle=1.50;
float dt=0.005;
float comp_filter(float newAngle, float newRate) {
dt=(millis()-lastCompTime)/1000.0;
float filterTerm0;
float filterTerm1;
float filterTerm2;
float timeConstant;
timeConstant=0.5;
filterTerm0 = (newAngle - filterAngle) * timeConstant * timeConstant;
filterTerm2 += filterTerm0 * dt;
filterTerm1 = filterTerm2 + ((newAngle - filterAngle) * 2 * timeConstant) + newRate;
filterAngle = (filterTerm1 * dt) + filterAngle;
lastCompTime=millis();
return filterAngle;
}
Работает не идеально, но достаточно хорошо для данной задачи.
Следующий сенсор — квадратурный энкодер на моторе. Он генерирует прямоугольные импульсы на 2х своих выводах:

Считать их можно либо прерываниями, либо считыванием значений в цикле. На arduino playground есть замечательная статья с примерами кода.
Осталось получить угловую скорость колеса. Тут на помощь приходит школьная формула пройденное расстояние/затраченное время.
#define ToPhiRad(x) ((x)*0.00280357142)
timer_old = timer;
timer=millis();
G_Dt = (timer-timer_old)/1000.0;
dPhi=(ToPhiRad(encoder0Pos)-lastPhi)/G_Dt;
ToPhiRad переводит количество тиков энкодера в угол колеса, мой энкодер выдает около 2240 тиков на оборот. Чтобы получить угол нужно умножить тики на 2 Пи и разделить на их количество при полном обороте колеса.
Показания сенсоров поступают в LQR регулятор:
float K1=0.1,K2=0.29,K3=6.5,K4=1.12;
long getLQRSpeed(float phi,float dphi,float angle,float dangle){
return constrain((phi*K1+dphi*K2+K3*angle+dangle*K4)*285,-400,400);
}
Коэффициенты взяты из Matlab, правда для большей стабильности я подправил 2 первых коэффициента.
Мой драйвер, вернее его библиотека, принимает значения от -400 до 400. Я предположил, что на 400 он выдает на мотор 12В, т.е. мотор развивает максимальный момент (1.4Нм). Разделив 400 на 1.4 получаем коэффициент перевода из Нм, которые выдает LQR, в значения, понятные драйверу.
Просто стабилизировать робота в одной точке не очень интересно, поэтому к нему добавился BT-модуль HC-05. Модуль подключается к серийному порту микроконтроллера. Он работает на 3.3В, а arduino на 5В, поэтому подключать принимающий вход модуля надо через делитель напряжения. Вот схема подключения:

Во время цикла микроконтроллер опрашивает модуль на предмет символов:
float phiDif=0.f;
float factorDif=0.f;
float getPhiAdding(float dif){ //сколько прибавлять к углу колес для движения вперед-назад
if(dif<200 && dif>-200){return 0.f;}
float ret = dif*0.08;
return ret;
}
float getFactorAdding(float dif){//сколько добавлять к управлению для поворота
if(dif<200 && dif>-200){return 0.f;}
float ret = dif/500*20;
return ret;
}
//========
if (Serial.available()){
BluetoothData=Serial.read();
if(BluetoothData=='w'){
phiDif=200;
} else if(BluetoothData=='s'){
phiDif=-200;
} else if(BluetoothData=='a'){
factorDif=200;
} else if(BluetoothData=='d'){
factorDif=-200;
} else if(BluetoothData=='c'){
factorDif=0;
phiDif=0;
}
}
В конечном итоге показания сенсоров поступают в регулятор, а его управление и воздействие пользователя поступают на моторы:
encoder0Pos+=getPhiAdding(phiDif);
lastPhi=ToPhiRad(encoder0Pos);
spd=getLQRSpeed(ToPhiRad(encoder0Pos),dPhi,balanceAt-angle,gyroRate[coordY]);
float factorL=getFactorAdding(factorDif);
md.setSpeeds(spd-factorL,spd+factorL);
Раз в 50 миллисекунд посылается телеметрия-угол робота:
if(millis()%50==0){
Serial.println(angle);
}
Добавляем радиоуправление
Управлять будем с телефона под android.

При запуске приложения попросим пользователя выбрать к кому подключаться, bt-модуль должен быть уже сопряжен с телефоном (стандартный код 1234).
BluetoothAdapter bluetooth;
String []boundedItems;
protected static final int RECIEVE_MESSAGE = 1;
@Override
protected void onCreate(Bundle savedInstanceState) {
//...
bluetooth = BluetoothAdapter.getDefaultAdapter();
if(bluetooth != null){
if (!bluetooth.isEnabled()) {
bluetooth.enable();
}
}
Set<BluetoothDevice> bounded=bluetooth.getBondedDevices();
boundedItems=new String[bounded.size()];
int i=0;
for (BluetoothDevice bluetoothDevice : bounded) {
boundedItems[i++]=bluetoothDevice.getName();
}
showListDialog();
//...
}
public void showListDialog(){
AlertDialog.Builder builder = new AlertDialog.Builder(this);
builder.setTitle("Pick a device");
builder.setItems(boundedItems, new DialogInterface.OnClickListener() {
public void onClick(DialogInterface dialog, int item) {
connectTo(item);
}
});
AlertDialog alert = builder.create();
alert.show();
}
После выбора устройства подключимся к нему:
private static final UUID MY_UUID = UUID.fromString("00001101-0000-1000-8000-00805F9B34FB");
BluetoothSocket btSocket;
public void connectTo(int id){
Set<BluetoothDevice> bounded=bluetooth.getBondedDevices();
for (BluetoothDevice bluetoothDevice : bounded) {
if(bluetoothDevice.getName().equalsIgnoreCase(boundedItems[id])){
try {
btSocket=bluetoothDevice.createRfcommSocketToServiceRecord(MY_UUID);
btSocket.connect();
ct=new ConnectionThread(btSocket);
ct.start();
} catch (IOException e) {
e.printStackTrace();
try {
btSocket.close();
} catch (IOException e1) {
e1.printStackTrace();
}
showListDialog();
}
return;
}
}
}
После подключения стартует поток, который занимается коммуникацией между приложением и роботом:
private class ConnectionThread extends Thread{
private final InputStream mmInStream;
private final BufferedReader br;
private final OutputStream mmOutStream;
public ConnectionThread(BluetoothSocket socket) throws IOException {
mmInStream = socket.getInputStream();
br=new BufferedReader(new InputStreamReader(mmInStream));
mmOutStream = socket.getOutputStream();
}
public void run() {
while (true) {
try {
String line=br.readLine();
h.obtainMessage(RECIEVE_MESSAGE, line).sendToTarget();
} catch (IOException e) {
e.printStackTrace();
}
}
}
public void sendCmd(char cmd){
try{
mmOutStream.write(cmd);
}catch (IOException e) {
e.printStackTrace();
}
}
}
Поток посылает сообщение основному потоку приложения через Handler, который определяется так:
h = new Handler() {
public void handleMessage(android.os.Message msg) {
switch (msg.what) {
case RECIEVE_MESSAGE:
String line=(String)msg.obj;
try{
float a=Float.parseFloat(line.trim());
balancerView.setAngle((float) (a-Math.PI/2.f));
}catch (Exception e) { }
break;
}
};
};
balancerView это потомок класса SurfaceView, он занимается выводом на экран текущего положения робота.
Вот его метод перерисовки:
public void draw(Canvas canvas) {
Paint paint=new Paint();
paint.setStrokeWidth(3);
canvas.save();
canvas.rotate((float) (angle*180.f/Math.PI), cx, cy);
paint.setColor(Color.BLACK);
canvas.drawRect(cx-15, cy-150, cx+15, cy, paint);
paint.setColor(Color.WHITE);
canvas.drawRect(cx-12, cy-147, cx+12, cy-3, paint);
paint.setColor(Color.BLACK);
canvas.drawCircle(cx, cy, 30, paint);
paint.setColor(Color.WHITE);
canvas.drawCircle(cx, cy, 25, paint);
canvas.restore();
}
Команды роботу посылаются при появлении событий onTouch, чтобы можно было управлять роботом удерживая кнопку.
@Override
public boolean onTouch(View v, MotionEvent me) {
if(me.getAction()==MotionEvent.ACTION_UP){
ct.sendCmd('c');
return false;
}
if(v==wB){
ct.sendCmd('w');
}else if(v==aB){
ct.sendCmd('a');
}else if(v==sB){
ct.sendCmd('s');
}else if(v==dB){
ct.sendCmd('d');
}
return false;
}
Заключение
Самое приятное во всей постройке это то, что математическая модель сошлась с физической реализацией. Сама постройка железки не представляет из себя какой-то сложности, однако подбор правильных моторов, высоты робота, массы груза сверху и синтезирование управления довольно интересная задача.
Как и обещал вывод уравнений движения перевернутого маятника на колесе: Вывод уравнений и немного о постройке
репозитарий на GitHub