В эпоху Big Data графическое представление многомерных данных является весьма актуальной задачей. Однако результат визуализации не всегда соответствует ожиданиям. Вот пример не самого наглядного графика для изображения многомерных данных «Ирисы Фишера»:

Это обыкновенная точечная диаграмма. Можно даже увидеть в ней закономерность. Есть группа точек (выделенный красным сорт setosa) которые явно выделяются на фоне остальных. Но сколько времени понадобилось, чтобы рассмотреть всю диаграмму и понять это? А здесь ведь только 4 измерения. Что будет, когда у вас будут данные с 10-ю измерениями? Не трудно догадаться, что тогда задача визуальной классификации станет намного сложнее.
Диаграммы Эндрюса
Дэвид Эндрюс (Andrews, David F.) в 1972-м году описал удобный способ визуализации многомерных данных. Суть данного метода такова:
Каждая точка представляется в виде ряда Фурье:
представляется в виде ряда Фурье:
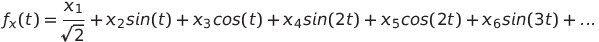
Получившаяся функция изображается на графике в промежутке
Таким образом, каждой точке из набора данных соответствует линия на графике в этом промежутке.
Возьмем для наглядности тот же набор данных, который использовался для точечной диаграммы выше, и изобразим эти данные с помощью диаграммы Эндрюса.

Можно заметить, что линии соответствующие похожим значениям также имеют и схожую форму. При этом размерность данных не имеет никакого значения, каждой точке всегда будет соответствовать одна линия на графике. Так же не составляет труда выделить сорт setosa (линии изображенные красным цветом) в отдельный класс. Главным достижением диаграммы Эндрюса в данном случае является, то, что мы получили понятное и легко читаемое представление наших данных.
Диаграммы Эндрюса далеко не единственная возможность визуализировать многомерные данные. Но этот метод прост в реализации, понятен и может без труда применяться на практике.
Список литературы:
● en.wikipedia.org/wiki/Andrews_plot
● Andrews, David F. (1972). «Plots of High-Dimensional Data». International Biometric Society 18 (1): 125–136. JSTOR 2528964.
● glowingpython.blogspot.ru/2014/10/andrews-curves.html

Это обыкновенная точечная диаграмма. Можно даже увидеть в ней закономерность. Есть группа точек (выделенный красным сорт setosa) которые явно выделяются на фоне остальных. Но сколько времени понадобилось, чтобы рассмотреть всю диаграмму и понять это? А здесь ведь только 4 измерения. Что будет, когда у вас будут данные с 10-ю измерениями? Не трудно догадаться, что тогда задача визуальной классификации станет намного сложнее.
Диаграммы Эндрюса
Дэвид Эндрюс (Andrews, David F.) в 1972-м году описал удобный способ визуализации многомерных данных. Суть данного метода такова:
Каждая точка
 представляется в виде ряда Фурье:
представляется в виде ряда Фурье: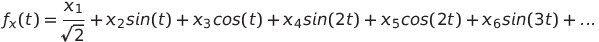
Получившаяся функция изображается на графике в промежутке

Таким образом, каждой точке из набора данных соответствует линия на графике в этом промежутке.
Возьмем для наглядности тот же набор данных, который использовался для точечной диаграммы выше, и изобразим эти данные с помощью диаграммы Эндрюса.
Код на ЯП Python
import numpy as np
import pylab as pl
def andrews_curve(x,theta):
curve = list()
for th in theta:
x1 = x[0] / np.sqrt(2)
x2 = x[1] * np.sin(th)
x3 = x[2] * np.cos(th)
x4 = x[3] * np.sin(2.*th)
curve.append(x1+x2+x3+x4)
return curve
accuracy = 1000
samples = np.loadtxt('iris.csv', usecols=[0,1,2,3], delimiter=',')
theta = np.linspace(-np.pi, np.pi, accuracy)
for s in samples[:20]: # setosa
pl.plot(theta, andrews_curve(s, theta), 'r')
for s in samples[50:70]: # versicolor
pl.plot(theta, andrews_curve(s ,theta), 'g')
for s in samples[100:120]: # virginica
pl.plot(theta, andrews_curve(s, theta), 'b')
pl.xlim(-np.pi,np.pi)
pl.show()

Можно заметить, что линии соответствующие похожим значениям также имеют и схожую форму. При этом размерность данных не имеет никакого значения, каждой точке всегда будет соответствовать одна линия на графике. Так же не составляет труда выделить сорт setosa (линии изображенные красным цветом) в отдельный класс. Главным достижением диаграммы Эндрюса в данном случае является, то, что мы получили понятное и легко читаемое представление наших данных.
Диаграммы Эндрюса далеко не единственная возможность визуализировать многомерные данные. Но этот метод прост в реализации, понятен и может без труда применяться на практике.
Список литературы:
● en.wikipedia.org/wiki/Andrews_plot
● Andrews, David F. (1972). «Plots of High-Dimensional Data». International Biometric Society 18 (1): 125–136. JSTOR 2528964.
● glowingpython.blogspot.ru/2014/10/andrews-curves.html