Мы с моим научным руководителем готовим небольшую монографию по обработке изображений. Решил представить на суд хабрасообщества главу, посвящённую алгоритмам сжатия изображений. Так как в рамках одного поста целую главу уместить тяжело, решил разбить её на три поста:
1. Методы сжатия данных;
2. Сжатие изображений без потерь;
3. Сжатие изображений с потерями.
Ниже вы можете ознакомиться с первым постом серии.
На текущий момент существует большое количество алгоритмов сжатия без потерь, которые условно можно разделить на две большие группы:
1. Поточные и словарные алгоритмы. К этой группе относятся алгоритмы семейств RLE (run-length encoding), LZ* и др. Особенностью всех алгоритмов этой группы является то, что при кодировании используется не информация о частотах символов в сообщении, а информация о последовательностях, встречавшихся ранее.
2. Алгоритмы статистического (энтропийного) сжатия. Эта группа алгоритмов сжимает информацию, используя неравномерность частот, с которыми различные символы встречаются в сообщении. К алгоритмам этой группы относятся алгоритмы арифметического и префиксного кодирования (с использованием деревьев Шеннона-Фанно, Хаффмана, секущих).
В отдельную группу можно выделить алгоритмы преобразования информации. Алгоритмы этой группы не производят непосредственного сжатия информации, но их применение значительно упрощает дальнейшее сжатие с использованием поточных, словарных и энтропийных алгоритмов.
Кодирование длин серий (RLE — Run-Length Encoding) — это один из самых простых и распространённых алгоритмов сжатия данных. В этом алгоритме последовательность повторяющихся символов заменяется символом и количеством его повторов.
Например, строку «ААААА», требующую для хранения 5 байт (при условии, что на хранение одного символа отводится байт), можно заменить на «5А», состоящую из двух байт. Очевидно, что этот алгоритм тем эффективнее, чем длиннее серия повторов.
Основным недостатком этого алгоритма является его крайне низкая эффективность на последовательностях неповторяющихся символов. Например, если рассмотреть последовательность «АБАБАБ» (6 байт), то после применения алгоритма RLE она превратится в «1А1Б1А1Б1А1Б» (12 байт). Для решения проблемы неповторяющихся символов существуют различные методы.
Самым простым методом является следующая модификация: байт, кодирующий количество повторов, должен хранить информацию не только о количестве повторов, но и об их наличии. Если первый бит равен 1, то следующие 7 бит указывают количество повторов соответствующего символа, а если первый бит равен 0, то следующие 7 бит показывают количество символов, которые надо взять без повтора. Если закодировать «АБАБАБ» с использованием данной модификации, то получим «-6АБАБАБ» (7 байт). Очевидно, что предложенная методика позволяет значительно повысить эффективность RLE алгоритма на неповторяющихся последовательностях символов. Реализация предложенного подхода приведена в Листинг 1:
Декодирование сжатого сообщения выполняется очень просто и сводится к однократному проходу по сжатому сообщению см. Листинг 2:
Вторым методом повышения эффективности алгоритма RLE является использование алгоритмов преобразования информации, которые непосредственно не сжимают данные, но приводят их к виду, более удобному для сжатия. В качестве примера такого алгоритма мы рассмотрим BWT-перестановку, названную по фамилиям изобретателей Burrows-Wheeler transform. Эта перестановка не изменяет сами символы, а изменяет только их порядок в строке, при этом повторяющиеся подстроки после применения перестановки собираются в плотные группы, которые гораздо лучше сжимаются с помощью алгоритма RLE. Прямое BWT преобразование сводится к последовательности следующих шагов:
1. Добавление к исходной строке специального символа конца строки, который нигде более не встречается;
2. Получение всех циклических перестановок исходной строки;
3. Сортировка полученных строк в лексикографическом порядке;
4. Возвращение последнего столбца полученной матрицы.
Реализация данного алгоритма приведена в Листинг 3.
Проще всего пояснить это преобразование на конкретном примере. Возьмём строку «АНАНАС» и договоримся, что символом конца строки будет символ «|». Все циклические перестановки этой строки и результат их лексикографической сортировки приведены в Табл. 1.
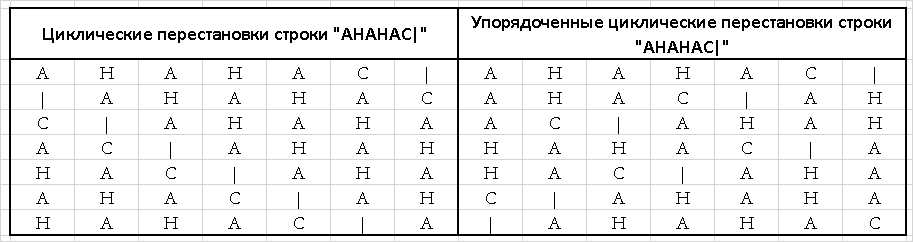
Т.е. результатом прямого преобразования будет строка «|ННАААС». Легко заметить, что это строка гораздо лучше, чем исходная, сжимается алгоритмом RLE, т.к. в ней существуют длинные подпоследовательности повторяющихся букв.
Подобного эффекта можно добиться и с помощью других преобразований, но преимущество BWT-преобразования в том, что оно обратимо, правда, обратное преобразование сложнее прямого. Для того, чтобы восстановить исходную строку, необходимо выполнить следующие действия:
Создать пустую матрицу размером n*n, где n-количество символов в закодированном сообщении;
Заполнить самый правый пустой столбец закодированным сообщением;
Отсортировать строки таблицы в лексикографическом порядке;
Повторять шаги 2-3, пока есть пустые столбцы;
Вернуть ту строку, которая заканчивается символом конца строки.
Реализация обратного преобразования на первый взгляд не представляет сложности, и один из вариантов реализации приведён в Листинг 4.
Но на практике эффективность зависит от выбранного алгоритма сортировки. Тривиальные алгоритмы с квадратичной сложностью, очевидно, крайне негативно скажутся на быстродействии, поэтому рекомендуется использовать эффективные алгоритмы.
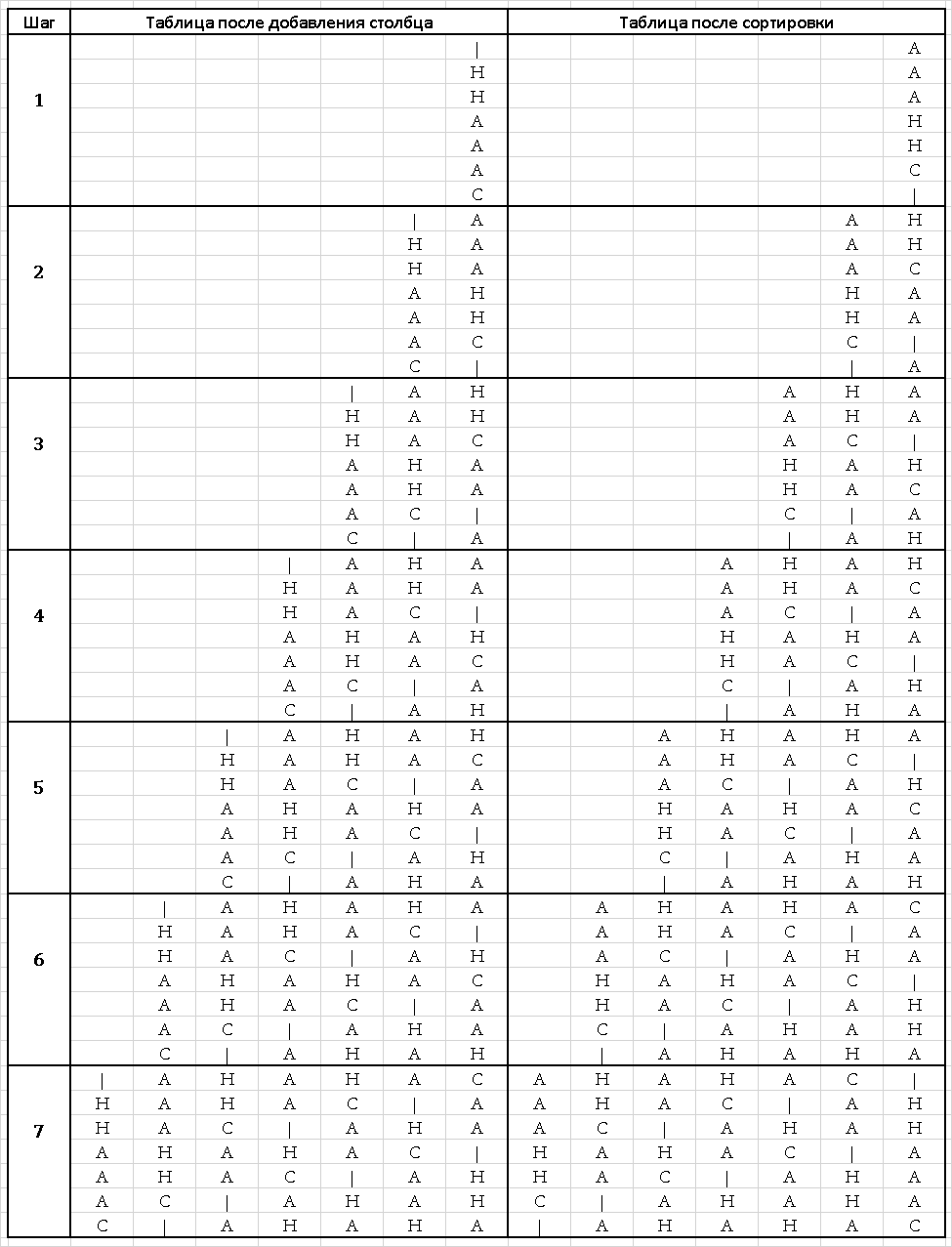
После сортировки таблицы, полученной на седьмом шаге, необходимо выбрать из таблицы строку, заканчивающуюся символом «|». Легко заметить, что это строка единственная. Т.о. мы на конкретном примере рассмотрели преобразование BWT.
Подводя итог, можно сказать, что основным плюсом группы алгоритмов RLE является простота и скорость работы (в том числе и скорость декодирования), а главным минусом является неэффективность на неповторяющихся наборах символов. Использование специальных перестановок повышает эффективность алгоритма, но также сильно увеличивает время работы (особенно декодирования).
Группа словарных алгоритмов, в отличие от алгоритмов группы RLE, кодирует не количество повторов символов, а встречавшиеся ранее последовательности символов. Во время работы рассматриваемых алгоритмов динамически создаётся таблица со списком уже встречавшихся последовательностей и соответствующих им кодов. Эту таблицу часто называют словарём, а соответствующую группу алгоритмов называют словарными.
Ниже описан простейший вариант словарного алгоритма:
Инициализировать словарь всеми символами, встречающимися во входной строке;
Найти в словаре самую длинную последовательность (S), совпадающую с началом кодируемого сообщения;
Выдать код найденной последовательности и удалить её из начала кодируемого сообщения;
Если не достигнут конец сообщения, считать очередной символ © и добавить Sc в словарь, перейти к шагу 2. Иначе, выход.
Например, только что инициализированный словарь для фразы «КУКУШКАКУКУШОНКУКУПИЛАКАПЮШОН» приведён в Табл. 3:
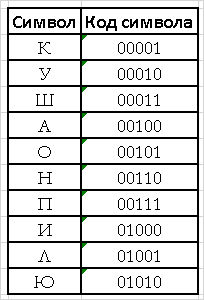
В процессе сжатия словарь будет дополняться встречающимися в сообщении последовательностями. Процесс пополнения словаря приведён в Табл. 4.

При описании алгоритма намеренно было опущено описание ситуации, когда словарь заполняется полностью. В зависимости от варианта алгоритма возможно различное поведение: полная или частичная очистка словаря, прекращение заполнение словаря или расширение словаря с соответствующим увеличением разрядности кода. Каждый из этих подходов имеет определённые недостатки. Например, прекращение пополнения словаря может привести к ситуации, когда в словаре хранятся последовательности, встречающиеся в начале сжимаемой строки, но не встречающиеся в дальнейшем. В то же время очистка словаря может привести к удалению частых последовательностей. Большинство используемых реализаций при заполнении словаря начинают отслеживать степень сжатия, и при её снижении ниже определённого уровня происходит перестройка словаря. Далее будет рассмотрена простейшая реализация, прекращающая пополнение словаря при его заполнении.
Для начала определим словарь как запись, хранящую не только встречавшиеся подстроки, но и количество хранящихся в словаре подстрок:
Встречавшиеся ранее подпоследовательности хранятся в массиве Words, а их кодом являются номера подпоследовательностей в этом массиве.
Также определим функции поиска в словаре и добавления в словарь:
Используя эти функции, процесс кодирования по описанному алгоритму можно реализовать следующим образом:
Результатом кодирования будут номера слов в словаре.
Процесс декодирования сводится к прямой расшифровке кодов, при этом нет необходимости передавать созданный словарь, достаточно, чтобы при декодировании словарь был инициализирован так же, как и при кодировании. Тогда словарь будет полностью восстановлен непосредственно в процессе декодирования путём конкатенации предыдущей подпоследовательности и текущего символа.
Единственная проблема возможна в следующей ситуации: когда необходимо декодировать подпоследовательность, которой ещё нет в словаре. Легко убедиться, что это возможно только в случае, когда необходимо извлечь подстроку, которая должна быть добавлена на текущем шаге. А это значит, что подстрока удовлетворяет шаблону cSc, т.е. начинается и заканчивается одним и тем же символом. При этом cS – это подстрока, добавленная на предыдущем шаге. Рассмотренная ситуация – единственная, когда необходимо декодировать ещё не добавленную строку. Учитывая вышесказанное, можно предложить следующий вариант декодирования сжатой строки:
К плюсам словарных алгоритмов относится их большая по сравнению с RLE эффективность сжатия. Тем не менее надо понимать, что реальное использование этих алгоритмов сопряжено с некоторыми трудностями реализации.
Алгоритм Шеннона-Фано — один из первых разработанных алгоритмов сжатия. В основе алгоритма лежит идея представления более частых символов с помощью более коротких кодов. При этом коды, полученные с помощью алгоритма Шеннона-Фано, обладают свойством префиксности: т.е. ни один код не является началом никакого другого кода. Свойство префиксности гарантирует, что кодирование будет взаимно-однозначным. Алгоритм построения кодов Шеннона-Фано представлен ниже:
1. Разбить алфавит на две части, суммарные вероятности символов в которых максимально близки друг к другу.
2. В префиксный код первой части символов добавить 0, в префиксный код второй части символов добавить 1.
3. Для каждой части (в которой не менее двух символов) рекурсивно выполнить шаги 1-3.
Несмотря на сравнительную простоту, алгоритм Шеннона-Фано не лишён недостатков, самым существенным из которых является неоптимальность кодирования. Хоть разбиение на каждом шаге и является оптимальным, алгоритм не гарантирует оптимального результата в целом. Рассмотрим, например, следующую строку: «ААААБВГДЕЖ». Соответствующее дерево Шеннона-Фано и коды, полученные на его основе, представлены на Рис. 1:
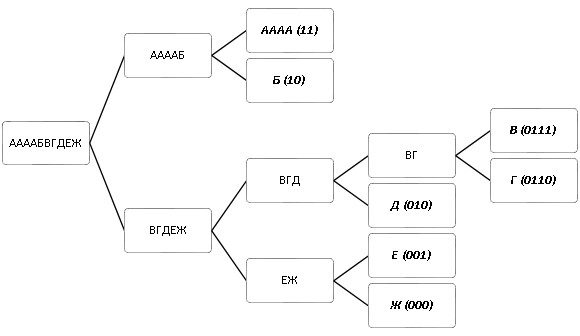
Без использования кодирования сообщение будет занимать 40 бит (при условии, что каждый символ кодируется 4 битами), а с использованием алгоритма Шеннона-Фано 4*2+2+4+4+3+3+3=27 бит. Объём сообщения уменьшился на 32.5%, но ниже будет показано, что этот результат можно значительно улучшить.
Алгоритм кодирования Хаффмана, разработанный через несколько лет после алгоритма Шеннона-Фано, тоже обладает свойством префиксности, а, кроме того, доказанной минимальной избыточностью, именно этим обусловлено его крайне широкое распространение. Для получения кодов Хаффмана используют следующий алгоритм:
1. Все символы алфавита представляются в виде свободных узлов, при этом вес узла пропорционален частоте символа в сообщении;
2. Из множества свободных узлов выбираются два узла с минимальным весом и создаётся новый (родительский) узел с весом, равным сумме весов выбранных узлов;
3. Выбранные узлы удаляются из списка свободных, а созданный на их основе родительский узел добавляется в этот список;
4. Шаги 2-3 повторяются до тех пор, пока в списке свободных больше одного узла;
5. На основе построенного дерева каждому символу алфавита присваивается префиксный код;
6. Сообщение кодируется полученными кодами.
Рассмотрим тот же пример, что и в случае с алгоритмом Шеннона-Фано. Дерево Хаффмана и коды, полученные для сообщения «ААААБВГДЕЖ», представлены на Рис. 2:
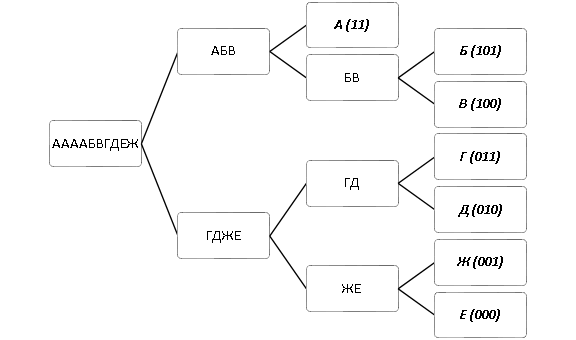
Легко подсчитать, что объём закодированного сообщения составит 26 бит, что меньше, чем в алгоритме Шеннона-Фано. Отдельно стоит отметить, что ввиду популярности алгоритма Хаффмана на данный момент существует множество вариантов кодирования Хаффмана, в том числе и адаптивное кодирование, которое не требует передачи частот символов.
Среди недостатков алгоритма Хаффмана значительную часть составляют проблемы, связанные со сложностью реализации. Использование для хранения частот символов вещественных переменных сопряжено с потерей точности, поэтому на практике часто используют целочисленные переменные, но, т.к. вес родительских узлов постоянно растёт, рано или поздно возникает переполнение. Т.о., несмотря на простоту алгоритма, его корректная реализация до сих пор может вызывать некоторые затруднения, особенно для больших алфавитов.
Кодирование с помощью секущих функций – разработанный авторами алгоритм, позволяющий получать префиксные коды. В основе алгоритма лежит идея построения дерева, каждый узел которого содержит секущую функцию. Чтобы подробнее описать алгоритм, необходимо ввести несколько определений.
Слово – упорядоченная последовательность из m бит (число m называют разрядностью слова).
Литерал секущей – пара вида разряд-значение разряда. Например, литерал (4,1) означает, что 4 бит слова должен быть равен 1. Если условие литерала выполняется, то литерал считается истинным, в противном случае — ложным.
k-разрядной секущей называют множество из k литералов. Если все литералы истинны, то и сама секущая функция истинная, в противном случае она ложная.
Дерево строится так, чтобы каждый узел делил алфавит на максимально близкие части. На Рис. 3 показан пример дерева секущих:
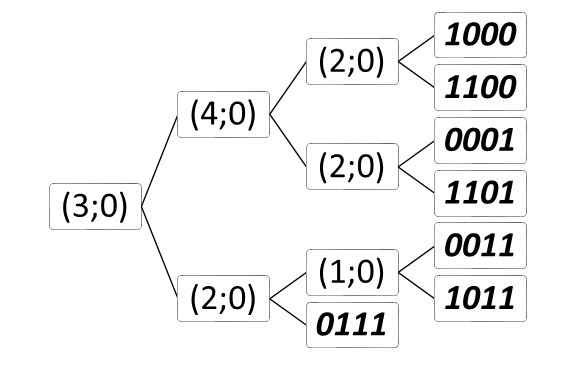
Дерево секущих функций в общем случае не гарантирует оптимального кодирования, но зато обеспечивает крайне высокую скорость работы за счёт простоты операции в узлах.
Арифметическое кодирование – один из наиболее эффективных способов сжатия информации. В отличие от алгоритма Хаффмана арифметическое кодирование позволяет кодировать сообщения с энтропией меньше 1 бита на символ. Т.к. большинство алгоритмов арифметического кодирования защищены патентами, далее будут описаны только основные идеи.
Предположим, что в используемом алфавите N символов a_1,…,a_N, с частотами p_1,…,p_N, соответственно. Тогда алгоритм арифметического кодирования будет выглядеть следующим образом:
В качестве рабочего полуинтервала взять [0;1);
Разбить рабочий полуинтервал на N непересекающихся полуинтервалов. При этом длина i-ого полуинтервала пропорциональна p_i.
Если не достигнут конец сообщения, в качестве нового рабочего интервала выбрать i-ый полуинтервал и перейти к шагу 2. В противном случае, вернуть любое число из рабочего полуинтервала. Запись этого числа в двоичном коде и будет представлять собой закодированное сообщение.
На Рис. 4 представлен процесс кодирования сообщения «АБААВ»
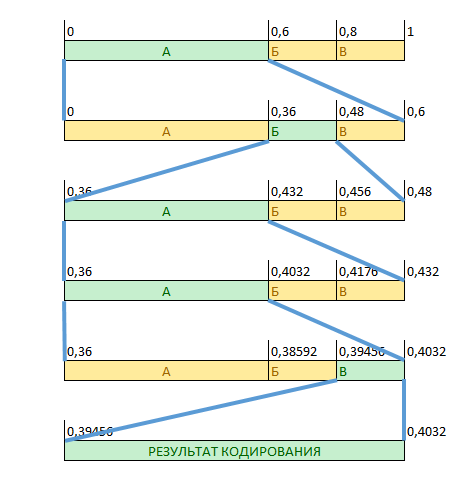
При декодировании необходимо выполнить аналогичную последовательность действий, только на каждом шаге необходимо дополнительно определять, какой именно символ был закодирован.
Очевидным плюсом арифметического кодирования является его эффективность, а основным (за исключением патентных ограничений) минусом – чрезвычайно высокая сложность процессов кодирования и декодирования.
1. Методы сжатия данных;
2. Сжатие изображений без потерь;
3. Сжатие изображений с потерями.
Ниже вы можете ознакомиться с первым постом серии.
На текущий момент существует большое количество алгоритмов сжатия без потерь, которые условно можно разделить на две большие группы:
1. Поточные и словарные алгоритмы. К этой группе относятся алгоритмы семейств RLE (run-length encoding), LZ* и др. Особенностью всех алгоритмов этой группы является то, что при кодировании используется не информация о частотах символов в сообщении, а информация о последовательностях, встречавшихся ранее.
2. Алгоритмы статистического (энтропийного) сжатия. Эта группа алгоритмов сжимает информацию, используя неравномерность частот, с которыми различные символы встречаются в сообщении. К алгоритмам этой группы относятся алгоритмы арифметического и префиксного кодирования (с использованием деревьев Шеннона-Фанно, Хаффмана, секущих).
В отдельную группу можно выделить алгоритмы преобразования информации. Алгоритмы этой группы не производят непосредственного сжатия информации, но их применение значительно упрощает дальнейшее сжатие с использованием поточных, словарных и энтропийных алгоритмов.
Поточные и словарные алгоритмы
Кодирование длин серий
Кодирование длин серий (RLE — Run-Length Encoding) — это один из самых простых и распространённых алгоритмов сжатия данных. В этом алгоритме последовательность повторяющихся символов заменяется символом и количеством его повторов.
Например, строку «ААААА», требующую для хранения 5 байт (при условии, что на хранение одного символа отводится байт), можно заменить на «5А», состоящую из двух байт. Очевидно, что этот алгоритм тем эффективнее, чем длиннее серия повторов.
Основным недостатком этого алгоритма является его крайне низкая эффективность на последовательностях неповторяющихся символов. Например, если рассмотреть последовательность «АБАБАБ» (6 байт), то после применения алгоритма RLE она превратится в «1А1Б1А1Б1А1Б» (12 байт). Для решения проблемы неповторяющихся символов существуют различные методы.
Самым простым методом является следующая модификация: байт, кодирующий количество повторов, должен хранить информацию не только о количестве повторов, но и об их наличии. Если первый бит равен 1, то следующие 7 бит указывают количество повторов соответствующего символа, а если первый бит равен 0, то следующие 7 бит показывают количество символов, которые надо взять без повтора. Если закодировать «АБАБАБ» с использованием данной модификации, то получим «-6АБАБАБ» (7 байт). Очевидно, что предложенная методика позволяет значительно повысить эффективность RLE алгоритма на неповторяющихся последовательностях символов. Реализация предложенного подхода приведена в Листинг 1:
- type
- TRLEEncodedString = array of byte;
- function RLEEncode(InMsg: ShortString): TRLEEncodedString;
- var
- MatchFl: boolean;
- MatchCount: shortint;
- EncodedString: TRLEEncodedString;
- N, i: byte;
- begin
- N := 0;
- SetLength(EncodedString, 2 * length(InMsg));
- while length(InMsg) >= 1 do
- begin
- MatchFl := (length(InMsg) > 1) and (InMsg[1] = InMsg[2]);
- MatchCount := 1;
- while (MatchCount <= 126) and (MatchCount < length(InMsg)) and ((InMsg[MatchCount] = InMsg[MatchCount + 1]) = MatchFl) do
- MatchCount := MatchCount + 1;
- if MatchFl then
- begin
- N := N + 2;
- EncodedString[N - 2] := MatchCount + 128;
- EncodedString[N - 1] := ord(InMsg[1]);
- end
- else
- begin
- if MatchCount <> length(InMsg) then
- MatchCount := MatchCount - 1;
- N := N + 1 + MatchCount;
- EncodedString[N - 1 - MatchCount] := -MatchCount + 128;
- for i := 1 to MatchCount do
- EncodedString[N - 1 - MatchCount + i] := ord(InMsg[i]);
- end;
- delete(InMsg, 1, MatchCount);
- end;
- SetLength(EncodedString, N);
- RLEEncode := EncodedString;
- end;
Декодирование сжатого сообщения выполняется очень просто и сводится к однократному проходу по сжатому сообщению см. Листинг 2:
- type
- TRLEEncodedString = array of byte;
- function RLEDecode(InMsg: TRLEEncodedString): ShortString;
- var
- RepeatCount: shortint;
- i, j: word;
- OutMsg: ShortString;
- begin
- OutMsg := '';
- i := 0;
- while i < length(InMsg) do
- begin
- RepeatCount := InMsg[i] - 128;
- i := i + 1;
- if RepeatCount < 0 then
- begin
- RepeatCount := abs(RepeatCount);
- for j := i to i + RepeatCount - 1 do
- OutMsg := OutMsg + chr(InMsg[j]);
- i := i + RepeatCount;
- end
- else
- begin
- for j := 1 to RepeatCount do
- OutMsg := OutMsg + chr(InMsg[i]);
- i := i + 1;
- end;
- end;
- RLEDecode := OutMsg;
- end;
Вторым методом повышения эффективности алгоритма RLE является использование алгоритмов преобразования информации, которые непосредственно не сжимают данные, но приводят их к виду, более удобному для сжатия. В качестве примера такого алгоритма мы рассмотрим BWT-перестановку, названную по фамилиям изобретателей Burrows-Wheeler transform. Эта перестановка не изменяет сами символы, а изменяет только их порядок в строке, при этом повторяющиеся подстроки после применения перестановки собираются в плотные группы, которые гораздо лучше сжимаются с помощью алгоритма RLE. Прямое BWT преобразование сводится к последовательности следующих шагов:
1. Добавление к исходной строке специального символа конца строки, который нигде более не встречается;
2. Получение всех циклических перестановок исходной строки;
3. Сортировка полученных строк в лексикографическом порядке;
4. Возвращение последнего столбца полученной матрицы.
Реализация данного алгоритма приведена в Листинг 3.
- const
- EOMsg = '|';
- function BWTEncode(InMsg: ShortString): ShortString;
- var
- OutMsg: ShortString;
- ShiftTable: array of ShortString;
- LastChar: ANSIChar;
- N, i: word;
- begin
- InMsg := InMsg + EOMsg;
- N := length(InMsg);
- SetLength(ShiftTable, N + 1);
- ShiftTable[1] := InMsg;
- for i := 2 to N do
- begin
- LastChar := InMsg[N];
- InMsg := LastChar + copy(InMsg, 1, N - 1);
- ShiftTable[i] := InMsg;
- end;
- Sort(ShiftTable);
- OutMsg := '';
- for i := 1 to N do
- OutMsg := OutMsg + ShiftTable[i][N];
- BWTEncode := OutMsg;
- end;
Проще всего пояснить это преобразование на конкретном примере. Возьмём строку «АНАНАС» и договоримся, что символом конца строки будет символ «|». Все циклические перестановки этой строки и результат их лексикографической сортировки приведены в Табл. 1.

Т.е. результатом прямого преобразования будет строка «|ННАААС». Легко заметить, что это строка гораздо лучше, чем исходная, сжимается алгоритмом RLE, т.к. в ней существуют длинные подпоследовательности повторяющихся букв.
Подобного эффекта можно добиться и с помощью других преобразований, но преимущество BWT-преобразования в том, что оно обратимо, правда, обратное преобразование сложнее прямого. Для того, чтобы восстановить исходную строку, необходимо выполнить следующие действия:
Создать пустую матрицу размером n*n, где n-количество символов в закодированном сообщении;
Заполнить самый правый пустой столбец закодированным сообщением;
Отсортировать строки таблицы в лексикографическом порядке;
Повторять шаги 2-3, пока есть пустые столбцы;
Вернуть ту строку, которая заканчивается символом конца строки.
Реализация обратного преобразования на первый взгляд не представляет сложности, и один из вариантов реализации приведён в Листинг 4.
- const
- EOMsg = '|';
- function BWTDecode(InMsg: ShortString): ShortString;
- var
- OutMsg: ShortString;
- ShiftTable: array of ShortString;
- N, i, j: word;
- begin
- OutMsg := '';
- N := length(InMsg);
- SetLength(ShiftTable, N + 1);
- for i := 0 to N do
- ShiftTable[i] := '';
- for i := 1 to N do
- begin
- for j := 1 to N do
- ShiftTable[j] := InMsg[j] + ShiftTable[j];
- Sort(ShiftTable);
- end;
- for i := 1 to N do
- if ShiftTable[i][N] = EOMsg then
- OutMsg := ShiftTable[i];
- delete(OutMsg, N, 1);
- BWTDecode := OutMsg;
- end;
Но на практике эффективность зависит от выбранного алгоритма сортировки. Тривиальные алгоритмы с квадратичной сложностью, очевидно, крайне негативно скажутся на быстродействии, поэтому рекомендуется использовать эффективные алгоритмы.

После сортировки таблицы, полученной на седьмом шаге, необходимо выбрать из таблицы строку, заканчивающуюся символом «|». Легко заметить, что это строка единственная. Т.о. мы на конкретном примере рассмотрели преобразование BWT.
Подводя итог, можно сказать, что основным плюсом группы алгоритмов RLE является простота и скорость работы (в том числе и скорость декодирования), а главным минусом является неэффективность на неповторяющихся наборах символов. Использование специальных перестановок повышает эффективность алгоритма, но также сильно увеличивает время работы (особенно декодирования).
Словарное сжатие (алгоритмы LZ)
Группа словарных алгоритмов, в отличие от алгоритмов группы RLE, кодирует не количество повторов символов, а встречавшиеся ранее последовательности символов. Во время работы рассматриваемых алгоритмов динамически создаётся таблица со списком уже встречавшихся последовательностей и соответствующих им кодов. Эту таблицу часто называют словарём, а соответствующую группу алгоритмов называют словарными.
Ниже описан простейший вариант словарного алгоритма:
Инициализировать словарь всеми символами, встречающимися во входной строке;
Найти в словаре самую длинную последовательность (S), совпадающую с началом кодируемого сообщения;
Выдать код найденной последовательности и удалить её из начала кодируемого сообщения;
Если не достигнут конец сообщения, считать очередной символ © и добавить Sc в словарь, перейти к шагу 2. Иначе, выход.
Например, только что инициализированный словарь для фразы «КУКУШКАКУКУШОНКУКУПИЛАКАПЮШОН» приведён в Табл. 3:

В процессе сжатия словарь будет дополняться встречающимися в сообщении последовательностями. Процесс пополнения словаря приведён в Табл. 4.

При описании алгоритма намеренно было опущено описание ситуации, когда словарь заполняется полностью. В зависимости от варианта алгоритма возможно различное поведение: полная или частичная очистка словаря, прекращение заполнение словаря или расширение словаря с соответствующим увеличением разрядности кода. Каждый из этих подходов имеет определённые недостатки. Например, прекращение пополнения словаря может привести к ситуации, когда в словаре хранятся последовательности, встречающиеся в начале сжимаемой строки, но не встречающиеся в дальнейшем. В то же время очистка словаря может привести к удалению частых последовательностей. Большинство используемых реализаций при заполнении словаря начинают отслеживать степень сжатия, и при её снижении ниже определённого уровня происходит перестройка словаря. Далее будет рассмотрена простейшая реализация, прекращающая пополнение словаря при его заполнении.
Для начала определим словарь как запись, хранящую не только встречавшиеся подстроки, но и количество хранящихся в словаре подстрок:
- type
- TDictionary = record
- WordCount: byte;
- Words: array of string;
- end;
Встречавшиеся ранее подпоследовательности хранятся в массиве Words, а их кодом являются номера подпоследовательностей в этом массиве.
Также определим функции поиска в словаре и добавления в словарь:
- const
- MAX_DICT_LENGTH = 256;
- function FindInDict(D: TDictionary; str: ShortString): integer;
- var
- r: integer;
- i: integer;
- fl: boolean;
- begin
- r := -1;
- if D.WordCount > 0 then
- begin
- i := D.WordCount;
- fl := false;
- while (not fl) and (i >= 0) do
- begin
- i := i - 1;
- fl := D.Words[i] = str;
- end;
- end;
- if fl then
- r := i;
- FindInDict := r;
- end;
- procedure AddToDict(var D: TDictionary; str: ShortString);
- begin
- if D.WordCount < MAX_DICT_LENGTH then
- begin
- D.WordCount := D.WordCount + 1;
- SetLength(D.Words, D.WordCount);
- D.Words[D.WordCount - 1] := str;
- end;
- end;
Используя эти функции, процесс кодирования по описанному алгоритму можно реализовать следующим образом:
- function LZWEncode(InMsg: ShortString): TEncodedString;
- var
- OutMsg: TEncodedString;
- tmpstr: ShortString;
- D: TDictionary;
- i, N: byte;
- begin
- SetLength(OutMsg, length(InMsg));
- N := 0;
- InitDict(D);
- while length(InMsg) > 0 do
- begin
- tmpstr := InMsg[1];
- while (FindInDict(D, tmpstr) >= 0) and (length(InMsg) > length(tmpstr)) do
- tmpstr := tmpstr + InMsg[length(tmpstr) + 1];
- if FindInDict(D, tmpstr) < 0 then
- delete(tmpstr, length(tmpstr), 1);
- OutMsg[N] := FindInDict(D, tmpstr);
- N := N + 1;
- delete(InMsg, 1, length(tmpstr));
- if length(InMsg) > 0 then
- AddToDict(D, tmpstr + InMsg[1]);
- end;
- SetLength(OutMsg, N);
- LZWEncode := OutMsg;
- end;
Результатом кодирования будут номера слов в словаре.
Процесс декодирования сводится к прямой расшифровке кодов, при этом нет необходимости передавать созданный словарь, достаточно, чтобы при декодировании словарь был инициализирован так же, как и при кодировании. Тогда словарь будет полностью восстановлен непосредственно в процессе декодирования путём конкатенации предыдущей подпоследовательности и текущего символа.
Единственная проблема возможна в следующей ситуации: когда необходимо декодировать подпоследовательность, которой ещё нет в словаре. Легко убедиться, что это возможно только в случае, когда необходимо извлечь подстроку, которая должна быть добавлена на текущем шаге. А это значит, что подстрока удовлетворяет шаблону cSc, т.е. начинается и заканчивается одним и тем же символом. При этом cS – это подстрока, добавленная на предыдущем шаге. Рассмотренная ситуация – единственная, когда необходимо декодировать ещё не добавленную строку. Учитывая вышесказанное, можно предложить следующий вариант декодирования сжатой строки:
- function LZWDecode(InMsg: TEncodedString): ShortString;
- var
- D: TDictionary;
- OutMsg, tmpstr: ShortString;
- i: byte;
- begin
- OutMsg := '';
- tmpstr := '';
- InitDict(D);
- for i := 0 to length(InMsg) - 1 do
- begin
- if InMsg[i] >= D.WordCount then
- tmpstr := D.Words[InMsg[i - 1]] + D.Words[InMsg[i - 1]][1]
- else
- tmpstr := D.Words[InMsg[i]];
- OutMsg := OutMsg + tmpstr;
- if i > 0 then
- AddToDict(D, D.Words[InMsg[i - 1]] + tmpstr[1]);
- end;
- LZWDecode := OutMsg;
- end;
К плюсам словарных алгоритмов относится их большая по сравнению с RLE эффективность сжатия. Тем не менее надо понимать, что реальное использование этих алгоритмов сопряжено с некоторыми трудностями реализации.
Энтропийное кодирование
Кодирование с помощью деревьев Шеннона-Фано
Алгоритм Шеннона-Фано — один из первых разработанных алгоритмов сжатия. В основе алгоритма лежит идея представления более частых символов с помощью более коротких кодов. При этом коды, полученные с помощью алгоритма Шеннона-Фано, обладают свойством префиксности: т.е. ни один код не является началом никакого другого кода. Свойство префиксности гарантирует, что кодирование будет взаимно-однозначным. Алгоритм построения кодов Шеннона-Фано представлен ниже:
1. Разбить алфавит на две части, суммарные вероятности символов в которых максимально близки друг к другу.
2. В префиксный код первой части символов добавить 0, в префиксный код второй части символов добавить 1.
3. Для каждой части (в которой не менее двух символов) рекурсивно выполнить шаги 1-3.
Несмотря на сравнительную простоту, алгоритм Шеннона-Фано не лишён недостатков, самым существенным из которых является неоптимальность кодирования. Хоть разбиение на каждом шаге и является оптимальным, алгоритм не гарантирует оптимального результата в целом. Рассмотрим, например, следующую строку: «ААААБВГДЕЖ». Соответствующее дерево Шеннона-Фано и коды, полученные на его основе, представлены на Рис. 1:

Без использования кодирования сообщение будет занимать 40 бит (при условии, что каждый символ кодируется 4 битами), а с использованием алгоритма Шеннона-Фано 4*2+2+4+4+3+3+3=27 бит. Объём сообщения уменьшился на 32.5%, но ниже будет показано, что этот результат можно значительно улучшить.
Кодирование с помощью деревьев Хаффмана
Алгоритм кодирования Хаффмана, разработанный через несколько лет после алгоритма Шеннона-Фано, тоже обладает свойством префиксности, а, кроме того, доказанной минимальной избыточностью, именно этим обусловлено его крайне широкое распространение. Для получения кодов Хаффмана используют следующий алгоритм:
1. Все символы алфавита представляются в виде свободных узлов, при этом вес узла пропорционален частоте символа в сообщении;
2. Из множества свободных узлов выбираются два узла с минимальным весом и создаётся новый (родительский) узел с весом, равным сумме весов выбранных узлов;
3. Выбранные узлы удаляются из списка свободных, а созданный на их основе родительский узел добавляется в этот список;
4. Шаги 2-3 повторяются до тех пор, пока в списке свободных больше одного узла;
5. На основе построенного дерева каждому символу алфавита присваивается префиксный код;
6. Сообщение кодируется полученными кодами.
Рассмотрим тот же пример, что и в случае с алгоритмом Шеннона-Фано. Дерево Хаффмана и коды, полученные для сообщения «ААААБВГДЕЖ», представлены на Рис. 2:

Легко подсчитать, что объём закодированного сообщения составит 26 бит, что меньше, чем в алгоритме Шеннона-Фано. Отдельно стоит отметить, что ввиду популярности алгоритма Хаффмана на данный момент существует множество вариантов кодирования Хаффмана, в том числе и адаптивное кодирование, которое не требует передачи частот символов.
Среди недостатков алгоритма Хаффмана значительную часть составляют проблемы, связанные со сложностью реализации. Использование для хранения частот символов вещественных переменных сопряжено с потерей точности, поэтому на практике часто используют целочисленные переменные, но, т.к. вес родительских узлов постоянно растёт, рано или поздно возникает переполнение. Т.о., несмотря на простоту алгоритма, его корректная реализация до сих пор может вызывать некоторые затруднения, особенно для больших алфавитов.
Кодирование с помощью деревьев секущих функций
Кодирование с помощью секущих функций – разработанный авторами алгоритм, позволяющий получать префиксные коды. В основе алгоритма лежит идея построения дерева, каждый узел которого содержит секущую функцию. Чтобы подробнее описать алгоритм, необходимо ввести несколько определений.
Слово – упорядоченная последовательность из m бит (число m называют разрядностью слова).
Литерал секущей – пара вида разряд-значение разряда. Например, литерал (4,1) означает, что 4 бит слова должен быть равен 1. Если условие литерала выполняется, то литерал считается истинным, в противном случае — ложным.
k-разрядной секущей называют множество из k литералов. Если все литералы истинны, то и сама секущая функция истинная, в противном случае она ложная.
Дерево строится так, чтобы каждый узел делил алфавит на максимально близкие части. На Рис. 3 показан пример дерева секущих:

Дерево секущих функций в общем случае не гарантирует оптимального кодирования, но зато обеспечивает крайне высокую скорость работы за счёт простоты операции в узлах.
Арифметическое кодирование
Арифметическое кодирование – один из наиболее эффективных способов сжатия информации. В отличие от алгоритма Хаффмана арифметическое кодирование позволяет кодировать сообщения с энтропией меньше 1 бита на символ. Т.к. большинство алгоритмов арифметического кодирования защищены патентами, далее будут описаны только основные идеи.
Предположим, что в используемом алфавите N символов a_1,…,a_N, с частотами p_1,…,p_N, соответственно. Тогда алгоритм арифметического кодирования будет выглядеть следующим образом:
В качестве рабочего полуинтервала взять [0;1);
Разбить рабочий полуинтервал на N непересекающихся полуинтервалов. При этом длина i-ого полуинтервала пропорциональна p_i.
Если не достигнут конец сообщения, в качестве нового рабочего интервала выбрать i-ый полуинтервал и перейти к шагу 2. В противном случае, вернуть любое число из рабочего полуинтервала. Запись этого числа в двоичном коде и будет представлять собой закодированное сообщение.
На Рис. 4 представлен процесс кодирования сообщения «АБААВ»

При декодировании необходимо выполнить аналогичную последовательность действий, только на каждом шаге необходимо дополнительно определять, какой именно символ был закодирован.
Очевидным плюсом арифметического кодирования является его эффективность, а основным (за исключением патентных ограничений) минусом – чрезвычайно высокая сложность процессов кодирования и декодирования.