В посте на своем блоге «gdal_translate и gdalwarp для перепроицирования изображений» описывался процесс получения картинок под разные проекции с помощью утилит GDAL. Полученные изображения я использовал как подложки для карт в примерах проекта dbCartajs. Позже, работая над портированием канвасной версии своего планетария на WebGL, описанной в статье «Звездное небо на WebGL с использованием Three.js» на Хабре, у меня возникла мысль со временем перенести не только глобус, но и плоские на карты на WebGL, используя вместо фона текстуры. То есть для создания карты обойтись только использованием браузера и JavaScript без использования серверных компонентов.
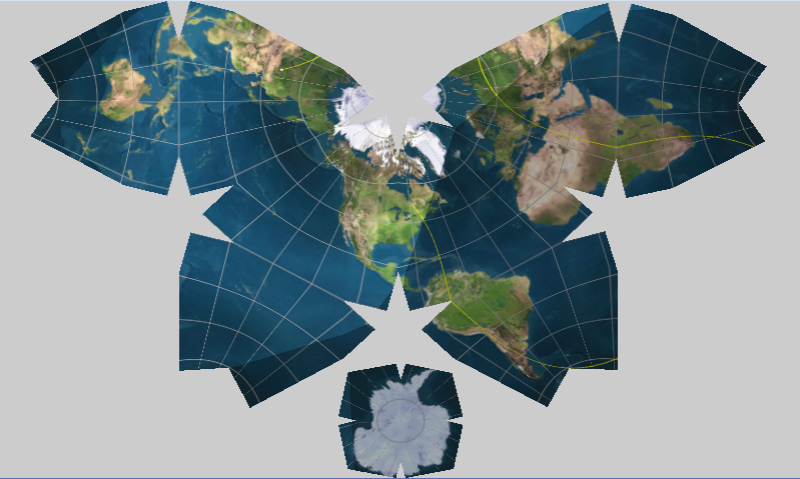
Мысль так и оставалась мыслью пока я не познакомился с очень интересным примером отображения картинки в разных проекциях на WebGL «Spinnable World Maps» от Марко Тарини. Этот пример показал коллега по работе еще год назад, но заинтересовался я им недавно. Код примера интересен еще и оригинальными комментариями автора на итальянском, типа punto centrale, mostra/nasconde griglia, movimento.
Код Марко Тарини оказался насыщен вычислениями всего чего угодно: размеров экрана, координат курсора мыши в пикселах и треугольниках, координат геометрий проекций, матриц поворота геометрий. При этом полностью картинка с меридианами и цветами формируется в шейдерах. Мне захотелось отрисовать что-нибудь на этой карте, скажем, границы стран. Но для этого пришлось бы вставлять код вычислений пикселов линий в код шейдера как с случае с меридианами, а это уже слишком. Поэтому возникла мысль совместить изображение карты в канвасе 2d с перепроицированием через WebGL и формулы Тарини. То есть использовать канвас как источник текстуры для наложения на геометрию. В исходниках Three.js встречаются такие примеры.
Из кода Spinnable Maps я взял в основном вычислительные функции:
Из примеров dbcartajs для канваса
Результат слияния двух проектов можно посмотреть в примере «Проекции 3d».
Управлять картой можно мышью. При таскании мышью происходит вращение карты по сфере по 3 осям, а не смещение на плоскости. Это порождает эффект бесконечного зацикливания карты вдоль оси X. Переключение проекций, а также управление слоями и аппаратами доступно через списки.

Мысль так и оставалась мыслью пока я не познакомился с очень интересным примером отображения картинки в разных проекциях на WebGL «Spinnable World Maps» от Марко Тарини. Этот пример показал коллега по работе еще год назад, но заинтересовался я им недавно. Код примера интересен еще и оригинальными комментариями автора на итальянском, типа punto centrale, mostra/nasconde griglia, movimento.
Код Марко Тарини оказался насыщен вычислениями всего чего угодно: размеров экрана, координат курсора мыши в пикселах и треугольниках, координат геометрий проекций, матриц поворота геометрий. При этом полностью картинка с меридианами и цветами формируется в шейдерах. Мне захотелось отрисовать что-нибудь на этой карте, скажем, границы стран. Но для этого пришлось бы вставлять код вычислений пикселов линий в код шейдера как с случае с меридианами, а это уже слишком. Поэтому возникла мысль совместить изображение карты в канвасе 2d с перепроицированием через WebGL и формулы Тарини. То есть использовать канвас как источник текстуры для наложения на геометрию. В исходниках Three.js встречаются такие примеры.
Из кода Spinnable Maps я взял в основном вычислительные функции:
- для расчета координат вершин (geometry.vertices) и треугольников (geometry.faces) геометрии: buildEquirectangular, buildCircleMap, buildLambert,…
- для расчета координат из массива VertexOnSphere: f_equirectangular, f_lambert, f_orthographic,… Массив VertexOnSphere передается в вершинный шейдер, где координаты XYZ преобразуются в XY для нарезания текстуры на треугольники. Собственно здесь и происходит перепроицирование картинки. Формулы схожи с расчетами из модуля Proj4js, который я использовал для канвасной 2d карты.
Из примеров dbcartajs для канваса
- логику создания карты по слоям
- пересчет координат мыши в пиксели
- таймер
Результат слияния двух проектов можно посмотреть в примере «Проекции 3d».
Управлять картой можно мышью. При таскании мышью происходит вращение карты по сфере по 3 осям, а не смещение на плоскости. Это порождает эффект бесконечного зацикливания карты вдоль оси X. Переключение проекций, а также управление слоями и аппаратами доступно через списки.