 Привет, Хабр!
Привет, Хабр!Большинство разработчиков знает, что такое Nested Sets, их сильные и слабые стороны. Сегодня я хочу представить на суд общественности реализацию модификации этой методики, которая частично решает недостатки оригинального алгоритма, правда имеет и свои отрицательные стороны.
Какие же плюсы и минусы у оригинальных Nested Sets:
+ быстрая выборка родителей и детей простым запросом;
+ быстрая выборка соседних узлов простым запросом;
+ быстрая выборка пустых узлов простым запросом;
+ моментальное получение количества всех детей в узле по формуле;
+ возможность не рекурсивного построения дерева одним циклом;
— очень медленная вставка и обновление.
Каковы же причины медленной вставки/обновления? Так как, значения границ узлов идут непрерывно, то любая вставка, особенно в начало дерева, требует перерасчёта границ всех последующих узлов. Если таблица достаточно большая, то это процесс может затянуться на десятки секунд и даже дольше. На анимации:

Nested Intervals
Первая мысль, которая пришла в голову, рассматривая картинку с визуальным представлением Nested Sets: «так границы же можно не двигать, если представить корневой узел как отрезок на поле вещественных чисел». То есть, если представить, что границы корневого узла имеют значения 0.0 и 1.0, то можно добавлять узлы в любое место не двигая другие, надо просто взять вещественное число между целевыми узлами. Но, так как мы прекрасно знаем, вещественные числа в компьютере имеют свои пределы, то от этой идеи я быстро отказался, в пользу целых чисел.
С целыми числами суть та же, только границы корневого узла сделаем от нуля до INT_MAX. Тогда при вставке нового узла мы просто берём любые два незанятых значения между целевыми узлами, и больше ничего не трогаем, всё было бы быстро и круто, если бы не одно «но» — что делать если свободных значений больше нет? Очевидно, что нужно двигать все значения границ до ближайшего свободного значения, «расчищая» себе пространство для вставки. Только вот поиск такой «дырки» — задача затратная, поэтому результат в таком случае может выйти даже медленнее, чем в классических nested sets.

Немного погуглив, я понял, что не изобрёл велосипед, и эта идея уже давно имеет название Nested Itervals. Только вот реализаций я так и не нашёл, т. к. на большинстве ресурсов данную методику рассматривали в негативном ключе, мол «одно лечим, другое калечим». И это не безосновательно, но мне стало очень интересно, захотелось протестировать в чём данный алгоритм лучше, а в чём хуже, и на сколько.
Реализация
Я начал писать Behavior для Yii2, реализующий идею Nested Intervals. Первая сложность возникла при написании методов вставки — как получить границу соседнего узла или родителя при
insertBefore() и insertAfter() и границу первого/последнего узла при prependTo() и appendTo()? Если в Nested Sets она очевидна — +1/-1 к границе текущего узла, то здесь без дополнительно запроса к базе никак. Но благо, что выборки у нас быстрые.Достаточно много времени ушло на реализацию поиска незанятого места, на случай, если места на вставку нового узла не хватает. Зато в результате я получил возможность двигать границы не половины базы, а лишь небольшого кусочка до почти ближайшей «дырки» от текущего отрезка.
Следующий большой вопрос возник при перемещении существующих ветвей в новое место. Если эта операция происходит в рамках одного дерева, то тут ещё можно всё быстро сделать, просто поменяв местами два блока.
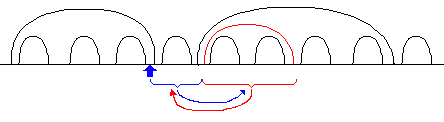
Но вот перемещение из другого дерева — задача оказалась трудно решаемая, т. к. перемещаемых узлов может оказаться очень много, и вставлять их по одному обычным алгоритмом выходит слишком долго. Сначала я вообще хотел отказаться от этой возможности, списав на сложность реализации. Но чуть позже, осознал необходимость метода
optimize(), который бы равномерно распределял границы существующих узлов по диапазону. После этого, возникла идея перемещать узлы другого дерева путём оптимизации исходного дерева с заготовлением «окна» под перемещаемые узлы. Всё это работает очень медленно (на данный момент есть оптимизация этого метода только под MySQL), но стоит отметить, что операция по перемещению из других деревьев требуется редко, куда чаще требуется движения в рамках одного дерева.Зато реализовывать выборки было достаточно легко — главные методы получения родителей и детей идентичны классическим nested sets. Чуть посложнее с выборками предыдущего/следующего соседа — требуется два запроса: получение родителя, и непосредственный поиск в диапазоне с лимитом. А вот совсем плохо стало с получением пустых узлов
getLeaves(), т. к. пришлось его делать с помощью left join, что наверняка скажется на производительности.Оптимизация вставки
Выполнив первый ряд тестов на производительность, результаты мягко говоря не впечатлили. Дело оказалось в том, что сначала я реализовал выбор границ вставляемого узла просто разбив отрезок на три части. Из-за этого промежуток для новых узлов стремительно сокращался. Так как диапазон 32 битного PHP составляет [0 — 2147483647] (операции с большими числами конвертируются во float), то выполнив вставку через
appendTo() всего 19-ти узлов в корень, на 20-й узел уже не останется места (2147483647/3^19 = ~1.9), и приходится выполнять медленные операции по поиску незанятых мест и перемещения. Так дело, конечно, не пойдёт. Нужны какие-то оптимизации по распределению места. Для этого в Behavior есть аж 5 опций:- Первая и главная
amountOptimize— этот параметр определяет на какое количество узлов запланировать разбиение доступного для вставки отрезка. То есть, при значении 20, мы сможем вставить 20 дочерних узлов, и они равномерно займут диапазон родителя, а дальше — как получится.
В качестве значения можно использовать массив, тогда значение будет разным для каждого уровня.
-
noPrepend,noAppend,noInsert— эти параметры помогают оптимизировать резервирование места между границами, и положение первого узла. Если у вас, используется в основном только операцияappendTo()(например, комментарии), то вы можете выставитьnoPrepend = trueиnoInsert = true, и тем самым значительно снизите вероятность возникновения тяжёлого случая с расчисткой пространства под новый узел. Более наглядно влияние этих параметров показано на картинках.
amountOptimize=3 
amountOptimize=3
noPrepend=true
amountOptimize=3
noAppend=true
amountOptimize=3
noInsert=true
amountOptimize=3
noInsert=true
noPrepend=true
amountOptimize=3
noInsert=true
noAppend=true
Стоит отметить, что если вы задаётеnoPrepend = true— это не значит, что вы не сможете выполнить вставкуprependTo(), просто с большой долей вероятности множество таких операций будут выполняться медленно.
- И последний параметр
reserveFactor, определяет размер промежутков между границами. При единичке размер промежутка равен размеру вставляемого узла. Если сценарий использования Behavior предполагает большого числа операцийinsertBefore()иinsertAfter(), то этот параметр лучше увеличить
После всех этих манипуляций тесты стали гораздо более «вкусными».
64 бита
Если вы задействуете BIGINT колонки для хранения
left и right атрибутов и используете 64-битный PHP, то сможете воспользоваться бесплатной оптимизацией в виде более широкого диапазона. Просто задайте параметр range = [0, 9223372036854775807]. Это позволит сделать более редкими случаи с недостатком места под новые узлы.Тесты на производительность
В качестве эталона для сравнения, был взят самый популярный Behavior, реализующий Nested Sets от уважаемого Alexander Kochetov (Creocoder) creocoder/yii2-nested-sets. Так же было интересно сравнить результаты с Adjacency List с сохранением возможности сортировки. Подходящей библиотеки я для этого не нашёл, поэтому взял и написал сам (да ещё и с поддержкой JOINов, но сейчас не об этом).
Первые два теста довольно синтетические, т. к. в реальности так заполнять дерево вряд ли кто будет, но мне данная процедура была необходима в первую очередь для генерации более-менее большой базы для дальнейших тестов. В них просто последовательно заполняются уровни фиксированным количеством детей.
Результаты тестов 1 и 2
Уже в первом тесте видно, как плохо влияет неподходящее значение параметра amountOptimize. В 32-битном тесте появились лишние запросы? связанные с тем, что для некоторых узлов скрипт «расчищал место». Но тем не менее, даже в этом случае всё выполнилось гораздо быстрее. Кстати 64-бита в этом тесте выручили, и не было ни одной «плохой» ситуации.
Запросов DB время Выполнение Память
Тест 1. Заполнение 3 уровня по 12 детей.
Nested Sets 7696 6,961 ms 26,305 ms 135.8 MB
Itervals default (amount=10) 6377 2,850 ms 11,920 ms 87.3 MB
Itervals x64 default (amount=10) 5813 1,992 ms 10,963 ms 78.7 MB
Itervals amount=24 5813 1,765 ms 10,442 ms 78.7 MB
Itervals amount=12 noPrepend noInsert 5813 1,750 ms 10,223 ms 78.7 MB
Adjacency List 5811 1,567 ms 9,591 ms 71.3 MB
Тест 2. Заполнение 6 уровня по 3 детей.
Nested Sets 4735 5,701 ms 19,784 ms 82.2 MB
Itervals default (amount=10) 3644 1,275 ms 5,976 ms 48.9 MB
Itervals amount=3 noPrepend noInsert 3644 1,271 ms 5,993 ms 48.9 MB
Adjacency List 3642 982 ms 5,812 ms 44.5 MB
Уже в первом тесте видно, как плохо влияет неподходящее значение параметра amountOptimize. В 32-битном тесте появились лишние запросы? связанные с тем, что для некоторых узлов скрипт «расчищал место». Но тем не менее, даже в этом случае всё выполнилось гораздо быстрее. Кстати 64-бита в этом тесте выручили, и не было ни одной «плохой» ситуации.
Тесты 3-5 имитируют вставку 20 узлов в разное место большой таблицы:
Результаты тестов 3-5
Тест на вставку в начало базы очень наглядно демонстрирует слабое место классических Nested Sets — для вставки в начало базы требуется обновление границ всей базы. Отсюда и разгромный результат. Лишь результаты вставки в конец базы более-менее конкурирует с Nested Itervals. И кстати, обратите внимание на то, что Adjacency List был медленнее, это связано с тем, что для обеспечения сортировки, ему приходится выполнять
Запросов DB время Выполнение Память
Тест 3. Вставка в начало <4% (20 в 19657 узлов)
Nested Sets 100 15,597 ms 16,636 ms 5.0 MB
Itervals 82 21 ms 150 ms 4.7 MB
Adjacency List 100 170 ms 439 ms 4.6 MB
Тест 4. Вставка в середину >46% <50% (20 в 19657 узлов)
Nested Sets 100 8,200 ms 8,985 ms 5.0 MB
Itervals 82 269 ms 593 ms 4.7 MB
Adjacency List 100 163 ms 454 ms 4.7 MB
Тест 5. Вставка в конец >96% (20 в 19657 узлов)
Nested Sets 100 549 ms 911 ms 5.0 MB
Itervals 83 46 ms 187 ms 4.7 MB
Adjacency List 106 159 ms 435 ms 4.7 MB
Тест на вставку в начало базы очень наглядно демонстрирует слабое место классических Nested Sets — для вставки в начало базы требуется обновление границ всей базы. Отсюда и разгромный результат. Лишь результаты вставки в конец базы более-менее конкурирует с Nested Itervals. И кстати, обратите внимание на то, что Adjacency List был медленнее, это связано с тем, что для обеспечения сортировки, ему приходится выполнять
SELECT MAX(sort).Следующий тест удаляет 20 узлов из начала дерева:
Результаты теста 6
Здесь ситуация аналогичная тесту 3. Есть лишь разница в том, что в Itervals при удалении уже не могут возникнуть «плохих ситуаций».
Запросов DB время Выполнение Память
Тест 6. Удаление из начала <4% (20 из 19657 узлов)
Nested Sets 100 16,554 ms 17,678 ms 4.8 MB
Itervals 60 164 ms 250 ms 4.2 MB
Adjacency List parentJoin=0 childrenJoin=0 60 169 ms 257 ms 3.8 MB
Adjacency List parentJoin=3 childrenJoin=3 60 87 ms 162 ms 3.8 MB
Здесь ситуация аналогичная тесту 3. Есть лишь разница в том, что в Itervals при удалении уже не могут возникнуть «плохих ситуаций».
Тест 7 очень показательный, т. к. хорошо имитирует использование Behavior для комментариев. В цикле 1000 узлов добавляется в случайно выбранный узел, с ограничением уровней. Тест 8 аналогичный, но с ещё более жесткими условиями — разрешено не только добавление, но и любая другая операция.
Результаты тестов 7 и 8
Тут в глаза бросается то, как важно при задействовании Intervals правильно настроить параметры оптимизации вставки, т. к. в данном примере настройки по умолчанию дали очень печальный результат. Зато с оптимизациями всё работает очень быстро, сопоставимо с Adjacency List. Кстати в 8 тесте он сильно замедлился, т. к. для обеспечения сортировки ему тоже требовалось «расчищать место».
Запросов DB время Выполнение Память
Тест 7. appendTo() в случайный узел (5 уровней, 1000 узлов)
Nested Sets 5002 5,989 ms 17,406 ms 80.7 MB
Itervals default (amount=10) 8497 23,301 ms 41,060 ms 120.7 MB
Itervals x64 default (amount=10) 7092 11,330 ms 23,618 ms 97.5 MB
Itervals amount=200,25 noPrepend noInsert 4009 1,431 ms 6,490 ms 50.2 MB
Itervals x64 amount=250,30 noPrepend noIns 4003 1,421 ms 6,615 ms 50.0 MB
Adjacency List 4001 1,062 ms 5,976 ms 46.1 MB
Тест 8. произвольная операция в случайный узел (5 уровней, 1000 узлов)
Nested Sets 5002 9,383 ms 23,502 ms 80.7 MB
Itervals default (amount=10) 7733 8,123 ms 24,031 ms 107.2 MB
Itervals x64 default (amount=10) 5663 3,761 ms 14,084 ms 75.6 MB
Itervals amount=200,25 reserve=2 4175 1,548 ms 7,223 ms 52.8 MB
Itervals x64 amount=250,30 reserve=2 4003 1,541 ms 6,753 ms 50.0 MB
Adjacency List 4395 4,394 ms 12,377 ms 53.4 MB
Тут в глаза бросается то, как важно при задействовании Intervals правильно настроить параметры оптимизации вставки, т. к. в данном примере настройки по умолчанию дали очень печальный результат. Зато с оптимизациями всё работает очень быстро, сопоставимо с Adjacency List. Кстати в 8 тесте он сильно замедлился, т. к. для обеспечения сортировки ему тоже требовалось «расчищать место».
Следующие два теста на перемещение узлов в дереве:
Результаты тестов 9 и 10
В принципе, что у Nested Sets, что у Nested Intervals эта операция должна выполняться за одинаковое время, но в коде у Creocoder это происходит не оптимально, т. к. вместо того, чтобы просто поменять местами пару блоков, в его коде сначала двигается вся база до конца, потом идёт перемещение нужного блока, а затем опять вся база двигается назад. Зато у Creocoder можно использовать unsigned поля для атрибута depth, а в моём Behavior он временно при перемещении становится отрицательным. Результаты перемещения из конца в начало сопоставимы, а вот Adjacency List имеет значительное преимущество.
Запросов DB время Выполнение Память
Тест 9. Перемещение узлов в начале <4% (20 из 19657 узлов)
Nested Sets 200 24,312 ms 25,479 ms 6.3 MB
Itervals 160 180 ms 573 ms 6.0 MB
Adjacency List 111 107 ms 318 ms 4.6 MB
Тест 10. Перемещение узлов из конца в начало <4% >96% (20 из 19657 узлов)
Nested Sets 200 16,999 ms 17,973 ms 6.3 MB
Itervals 160 16,972 ms 17,854 ms 6.0 MB
Adjacency List 108 86 ms 325 ms 4.6 MB
В принципе, что у Nested Sets, что у Nested Intervals эта операция должна выполняться за одинаковое время, но в коде у Creocoder это происходит не оптимально, т. к. вместо того, чтобы просто поменять местами пару блоков, в его коде сначала двигается вся база до конца, потом идёт перемещение нужного блока, а затем опять вся база двигается назад. Зато у Creocoder можно использовать unsigned поля для атрибута depth, а в моём Behavior он временно при перемещении становится отрицательным. Результаты перемещения из конца в начало сопоставимы, а вот Adjacency List имеет значительное преимущество.
После написания Behavior мне захотелось узнать, какую выгоду даст использование Trait вместо поведений. Поэтому я портировал его Trait со статическими атрибутами. Дальнейшие тесты на выборки велись также и в вариантах с Trait. Но результаты применения примесей мягко говоря не впечатлили, особенно учитывая то, насколько более уродлив стал код из-за них.
Простая выборка всех элементов
Model::find()->all():Результаты теста 11
Этот тест был написан в первую очередь для сравнения потребления памяти Behavior vs. Trait. И как видим разница есть, но незначительная.
Запросов DB время Выполнение Память
Тест 11. Выбор всех узлов (19657 шт.)
Nested Sets 1 40 ms 1,108 ms 215.2 MB
Itervals 1 42 ms 1,247 ms 225.3 MB
Itervals Trait 1 41 ms 1,174 ms 207.4 MB
Adjacency List 1 33 ms 890 ms 179.1 MB
Этот тест был написан в первую очередь для сравнения потребления памяти Behavior vs. Trait. И как видим разница есть, но незначительная.
Выборка потомков:
Результаты теста 12
Запросы на выборку детей должны быть одинаковыми в Nested Sets и Nested Intervals, но здесь раскрылся ещё один недостаток библиотеки от Creocoder — не оптимально выбираются потомки. Потомков можно было выбрать моментально используя индекс по одному из атрибутов left или right
Запросов DB время Выполнение Память
Тест 12. Выбор детей и потомков (для 819 узлов в середине дерева из 19657 узлов)
Nested Sets 1641 6,397 ms 7,498 ms 24.9 MB
Itervals Behavior 1641 579 ms 1,657 ms 25.0 MB
Itervals Trait 1641 615 ms 1,590 ms 24.3 MB
Adjacency List parentJoin=0 childrenJoin=0 2562 720 ms 1,969 ms 36.9 MB
Adjacency List parentJoin=3 childrenJoin=3 2461 704 ms 1,966 ms 35.3 MB
Запросы на выборку детей должны быть одинаковыми в Nested Sets и Nested Intervals, но здесь раскрылся ещё один недостаток библиотеки от Creocoder — не оптимально выбираются потомки. Потомков можно было выбрать моментально используя индекс по одному из атрибутов left или right
`lft` > :leftValue && `lft` < :rightValue, вместо этого, индекс используется лишь на половину `lft` > :leftValue && `rgt` < :rightValue. Если проанализировать EXPLAINом, становится ясно, что первый вариант гораздо более предпочтителен. Результаты Adjacency List уступают, что неудивительно.Выборка предков:
Результаты теста 13
Здесь Nested Sets и Nested Intervals ведут себя одинаково, и достаточно медленно. Дело в отсутствии нормальных индексов и неудачным стечением обстоятельств — оба индекса из середины таблицы имеют много элементов. Adjacency List как не удивительно, отработал быстрее, хоть и за счёт памяти (хотя тут дело ещё в простом 3-х уровневом дереве).
Запросов DB время Выполнение Память
Тест 13. Выборка родителей (для 819 узлов в середине дерева из 19657 узлов)
Nested Sets 821 3,344 ms 4,069 ms 20.6 MB
Itervals Behavior 821 3,292 ms 4,147 ms 22.0 MB
Itervals Trait 821 3,310 ms 4,080 ms 21.1 MB
Adjacency List parentJoin=0 childrenJoin=0 3180 948 ms 2,304 ms 51.2 MB
Adjacency List parentJoin=3 childrenJoin=3 1641 486 ms 1,495 ms 30.8 MB
Здесь Nested Sets и Nested Intervals ведут себя одинаково, и достаточно медленно. Дело в отсутствии нормальных индексов и неудачным стечением обстоятельств — оба индекса из середины таблицы имеют много элементов. Adjacency List как не удивительно, отработал быстрее, хоть и за счёт памяти (хотя тут дело ещё в простом 3-х уровневом дереве).
Выборка соседних и пустых узлов:
Результаты теста 14 и 15
Тут, как и предполагалось, мы видим слабые стороны Nested Intervals. Как говорится, без комментариев.
Запросов DB время Выполнение Память
Тест 14. Выборка соседних узлов (для 819 узлов в середине дерева из 19657 узлов)
Nested Sets 1641 520 ms 1,424 ms 24.3 MB
Itervals Behavior 1641 19,681 ms 21,326 ms 27.5 MB
Itervals Trait 1641 19,666 ms 21,251 ms 26.5 MB
Adjacency List parentJoin=0 childrenJoin=0 1641 535 ms 1,442 ms 23.7 MB
Adjacency List parentJoin=3 childrenJoin=3 1641 508 ms 1,421 ms 23.6 MB
Тест 15. Выборка пустых узлов (для 819 узлов в середине дерева из 19657 узлов)
Nested Sets 821 3,215 ms 3,814 ms 18.8 MB
Itervals Behavior 821 10,450 ms 11,166 ms 18.8 MB
Itervals Trait 821 10,425 ms 11,040 ms 18.7 MB
Adjacency List parentJoin=0 childrenJoin=0 1833 568 ms 1,743 ms 32.6 MB
Adjacency List parentJoin=3 childrenJoin=3 1732 556 ms 1,891 ms 31.3 MB
Тут, как и предполагалось, мы видим слабые стороны Nested Intervals. Как говорится, без комментариев.
Выводы
Nested Intervals — имеет право на жизнь. У него есть как преимущества, так и недостатки:
+ быстрая вставка (при условии хорошего подбора оптимизирующих параметров);
+ быстрое удаление узла с потомками;
+ такая же скорость как у Nested Sets в выборке предков и потомков;
+ так же, осталась возможность не рекурсивного построения дерева одним циклом;
— медленное получение соседних узлов;
— медленное получение пустых узлов;
— нет возможности моментально подсчитать количество потомков в узле.
Реализация для Yii2
Хочу отметить, что методы немного отличаются от предложенных в поведении Creocoder. Во-первых я изменил именование методов на геттеры
getParents() getDescendants(), это позволяет реализовывать доступ к связанным узлам, аналогично Relations, что позволяет не делать вторичных запросов к базе:$node = Node::findOne(['name' => 'test']);
$children = $node->children; // relation
$children = $node->getChildren()->all(); // query
Кроме того, я не стал протаскивать Yii-шные параметры к save($runValidation, $attributeNames), вместо этого я реализовал методы, как указание на действие (прямо как
->asArray()->):$node = new Node();
$node->makeRoot()->save(false);
$node->insertAfter($node2)->save();
Реализация Nested Intervals на GitHub.
Реализация Adjacency List на GitHub.