На днях столкнулся с интересной задачкой, которая показалась мне достойной аудитории данного ресурса. Условие ее следующее:
«Найти максимально допустимое отклонение массы конфеты при ее производстве, чтобы нетто коробки, состоящей из 12 штук их, не выходило за пределы 310±7 грамм в 90% случаев. Закон распределения считать нормальным.»
Стоит сказать, что условие не было выдернуто из интернета или подсмотрено на каком-нибудь ресурсе занимательных задач, а пришло от одного очень хорошего друга, который по должности своей инженер по организации и управлению производством на одной небезызвестной кондитерской фабрике. То есть задача имеет вполне реальное происхождение, а ее решение — практическую пользу.
Я предложил читателям решить задачу самостоятельно и должен сказать, что они справились с этим лучше меня. В своем же решении я я сделал не верное допущение.
Условимся обозначать большими буквами параметры для коробки и маленькими — для конфет.
Пускай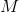 и
и  — соответственно масса нетто коробки и ее допустимое отклонение, такое, что в
— соответственно масса нетто коробки и ее допустимое отклонение, такое, что в 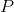 процентах случаев она не выходит за пределы
процентах случаев она не выходит за пределы 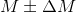 .
.
Пускай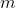 и
и 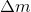 — соответственно масса конфеты и ее допустимое отклонение, такое, что в
— соответственно масса конфеты и ее допустимое отклонение, такое, что в  процентах случаев она не выходит за пределы
процентах случаев она не выходит за пределы 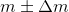 .
.
Количество конфет в коробке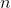 .
.
Нормальное распределение описывается функцией Гаусса:
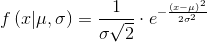
, где — математическое ожидание,
— математическое ожидание,  — стандартное отклонение, квадрат которого
— стандартное отклонение, квадрат которого 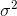 — называется дисперсией.
— называется дисперсией.
В случае с конфетами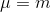 , a
, a 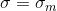 , поэтому:
, поэтому:
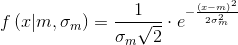
В случае с коробкой конфет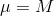 , a
, a 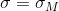 :
:
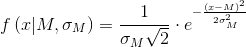
Вероятность того что масса конфеты не выйдет за пределы
того что масса конфеты не выйдет за пределы 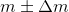 равна:
равна:
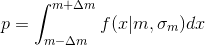
Вероятность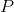 того что нетто коробки не выйдет за пределы
того что нетто коробки не выйдет за пределы 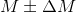 равна:
равна:
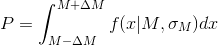
Рисунок ниже хорошо иллюстрирует все выше сказанное:
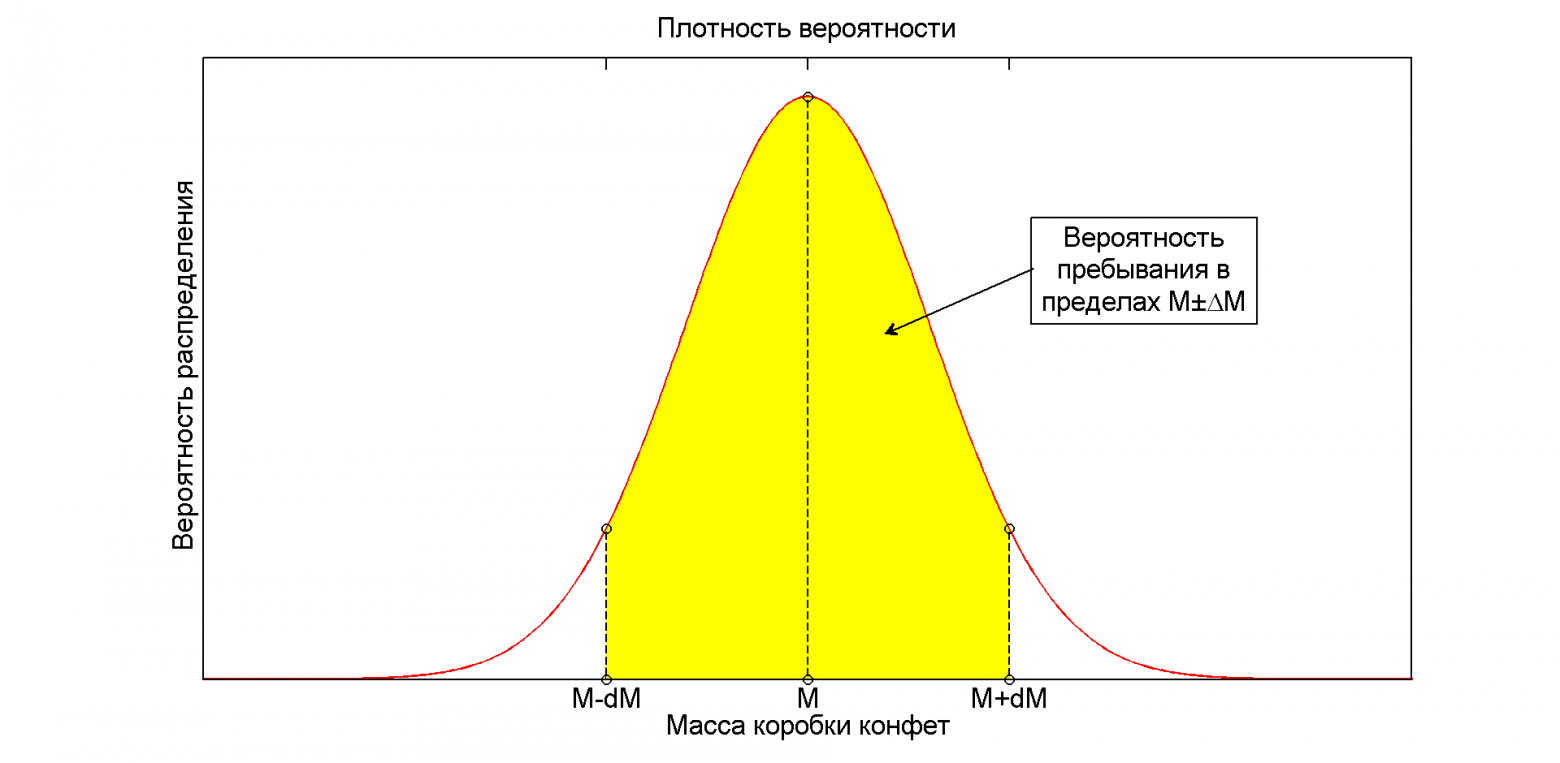
Найдем вероятность для конфеты:
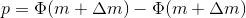
, где — функция распределения, а
— функция распределения, а 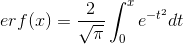 — функция ошибок.
— функция ошибок.
Таким образом для конфеты:
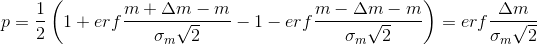
Аналогично для коробки:
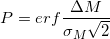
Из центральной предельной теоремы следует что если существуют независимые случайные величины:

, то их сумма:
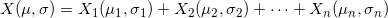
будет обладать параметрами:
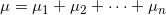
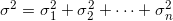
Применительно к нашей ситуации имеем:
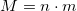
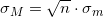
Я ошибочно посчитал что совокупная вероятность для коробки равна произведению вероятностей для отдельных конфет. Другими словами:
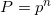
, откуда:
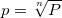
Получилась система уравнений:
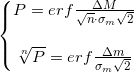
Решив ее относительно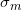 :
:
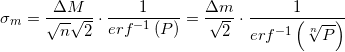
, вывел:
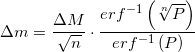
, где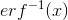 — обратная функция ошибок и нашел вполне конкретные цифры:
— обратная функция ошибок и нашел вполне конкретные цифры:
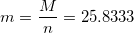
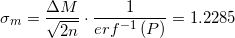
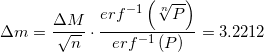
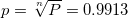
Такое решение я обосновал следующим образом: необходимо, чтобы масса конфеты не выходила за пределы 25.8333±3.2212 в 99.13% случаев (1 на 115). И хотя такой ответ не является противоречащим, правда в том что только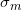 является верным ответом. Так как при таком и меньшем стандартном отклонении нам ничего не нужно отбрасывать, о чем многие читатели мне долго намекали и были правы.
является верным ответом. Так как при таком и меньшем стандартном отклонении нам ничего не нужно отбрасывать, о чем многие читатели мне долго намекали и были правы.
Как же без нее. Проверку состряпал в матлабе. Вкратце создаем 1000000 конфет с найденными параметрами по нормальному закону. Случайным (равновероятным) образом из них формируем 1000000 группок (считай коробок) по 12 штук. Проверяем количество таких групп не вышедших за пределы 310±7 и делим на общее, получая таким образом ту самую вероятность для коробки. И так 1000 раз.
В итоге получился такой вот красивый график:
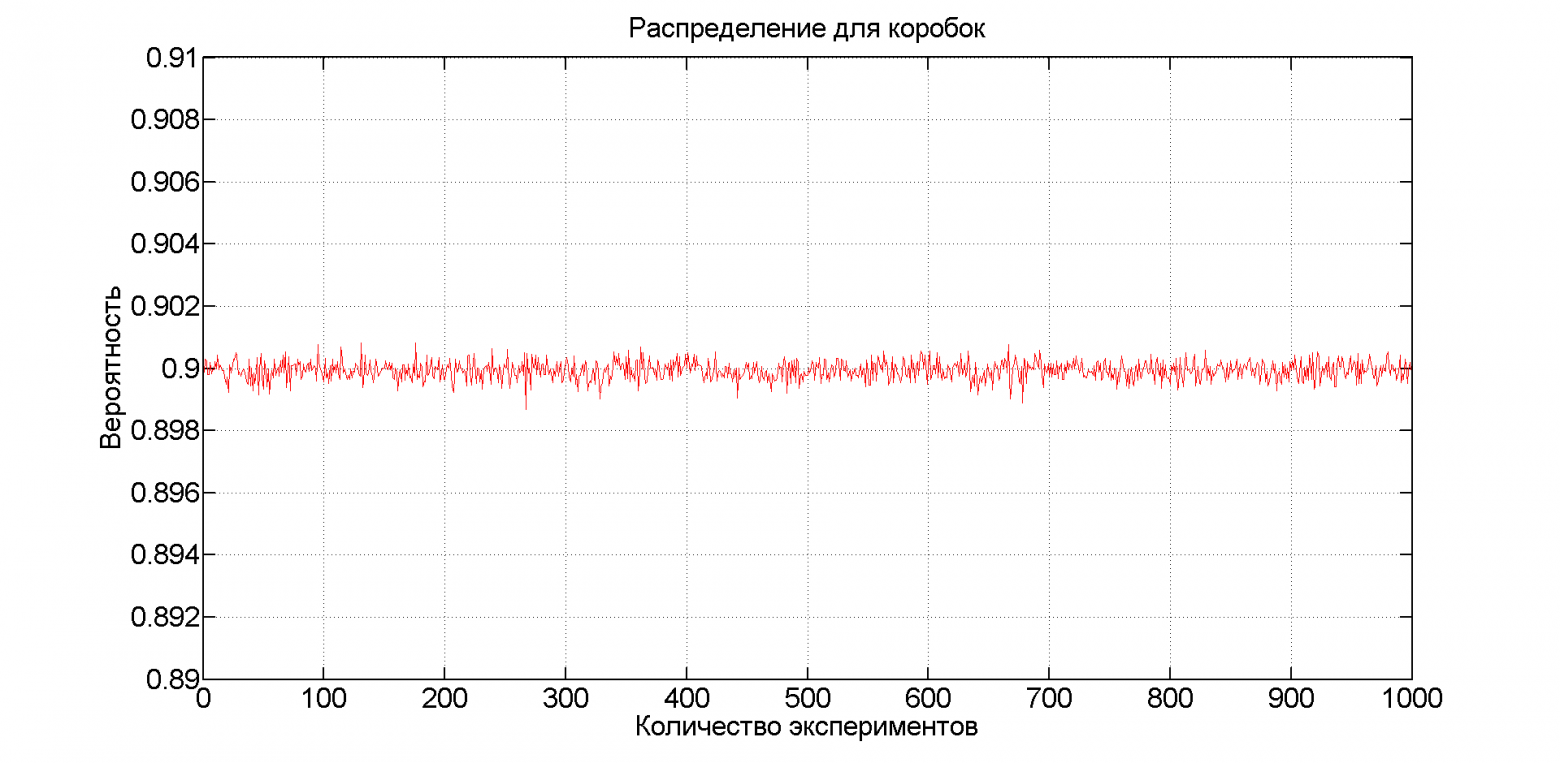
Осмелюсь предположить что 1 млн. коробок мало и если устремить их количество в бесконечность, наши вероятности будут ровно в 90%.
Гораздо интереснее случай, когда аппарат для разлива конфет имеет константное стандартное отклонение, которое больше 1.2285 и нужно найти те самые границы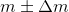 , выше которых, при заданной
, выше которых, при заданной 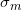 , конфеты нужно отбросить, чтобы удовлетворять тем же условиям. Это куда более сложная задача, которой я возможно посвящу еще одну статью.
, конфеты нужно отбросить, чтобы удовлетворять тем же условиям. Это куда более сложная задача, которой я возможно посвящу еще одну статью.
«Найти максимально допустимое отклонение массы конфеты при ее производстве, чтобы нетто коробки, состоящей из 12 штук их, не выходило за пределы 310±7 грамм в 90% случаев. Закон распределения считать нормальным.»
Стоит сказать, что условие не было выдернуто из интернета или подсмотрено на каком-нибудь ресурсе занимательных задач, а пришло от одного очень хорошего друга, который по должности своей инженер по организации и управлению производством на одной небезызвестной кондитерской фабрике. То есть задача имеет вполне реальное происхождение, а ее решение — практическую пользу.
Я предложил читателям решить задачу самостоятельно и должен сказать, что они справились с этим лучше меня. В своем же решении я я сделал не верное допущение.
1. Условности
Условимся обозначать большими буквами параметры для коробки и маленькими — для конфет.
Пускай
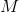 и
и  — соответственно масса нетто коробки и ее допустимое отклонение, такое, что в
— соответственно масса нетто коробки и ее допустимое отклонение, такое, что в 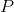 процентах случаев она не выходит за пределы
процентах случаев она не выходит за пределы 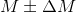 .
.Пускай
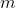 и
и 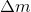 — соответственно масса конфеты и ее допустимое отклонение, такое, что в
— соответственно масса конфеты и ее допустимое отклонение, такое, что в 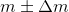 .
.Количество конфет в коробке
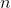 .
.2. Нормальное распределение
Нормальное распределение описывается функцией Гаусса:
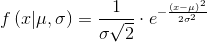
, где
 — математическое ожидание,
— математическое ожидание, 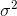 — называется дисперсией.
— называется дисперсией.В случае с конфетами
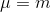 , a
, a 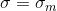 , поэтому:
, поэтому: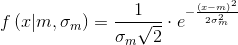
В случае с коробкой конфет
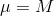 , a
, a 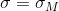 :
: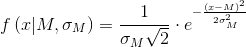
Вероятность
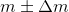 равна:
равна: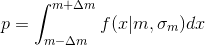
Вероятность
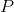 того что нетто коробки не выйдет за пределы
того что нетто коробки не выйдет за пределы 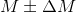 равна:
равна: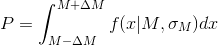
Рисунок ниже хорошо иллюстрирует все выше сказанное:

Найдем вероятность для конфеты:
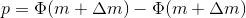
, где
 — функция распределения, а
— функция распределения, а 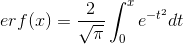 — функция ошибок.
— функция ошибок.Таким образом для конфеты:
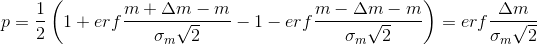
Аналогично для коробки:
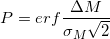
3. Центральная предельная теорема
Из центральной предельной теоремы следует что если существуют независимые случайные величины:

, то их сумма:
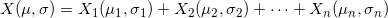
будет обладать параметрами:
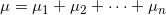
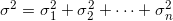
Применительно к нашей ситуации имеем:
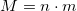
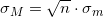
4. Вероятности и моя ошибка
Я ошибочно посчитал что совокупная вероятность для коробки равна произведению вероятностей для отдельных конфет. Другими словами:
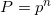
, откуда:
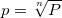
Получилась система уравнений:
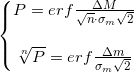
Решив ее относительно
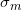 :
: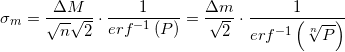
, вывел:
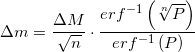
, где
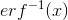 — обратная функция ошибок и нашел вполне конкретные цифры:
— обратная функция ошибок и нашел вполне конкретные цифры: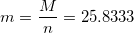
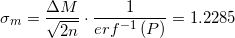
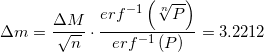
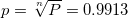
Такое решение я обосновал следующим образом: необходимо, чтобы масса конфеты не выходила за пределы 25.8333±3.2212 в 99.13% случаев (1 на 115). И хотя такой ответ не является противоречащим, правда в том что только
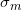 является верным ответом. Так как при таком и меньшем стандартном отклонении нам ничего не нужно отбрасывать, о чем многие читатели мне долго намекали и были правы.
является верным ответом. Так как при таком и меньшем стандартном отклонении нам ничего не нужно отбрасывать, о чем многие читатели мне долго намекали и были правы.5. Проверка
Как же без нее. Проверку состряпал в матлабе. Вкратце создаем 1000000 конфет с найденными параметрами по нормальному закону. Случайным (равновероятным) образом из них формируем 1000000 группок (считай коробок) по 12 штук. Проверяем количество таких групп не вышедших за пределы 310±7 и делим на общее, получая таким образом ту самую вероятность для коробки. И так 1000 раз.
Код
% Number of candys
nC = 1000000 ;
% Mass deviation of a single candy
mC = normrnd ( m , s , 1 , nC ) ;
% Number of candys in the box
n = 12 ;
% Number of boxes
nB = 1000000 ;
% Number of experiments
nE = 1000;
pB = zeros ( 1, nE );
for k = 1 : nE
% Random index of n candys
i = random ( 'unid' , nC , nB, n ) ;
% The mass of each boxes
j = 1 : nB ;
mB = sum ( mC ( i ( j , : ) ) , 2 )' ;
% Mask boxes that out of range
mask = ( mB < M + dM ) .* ( mB > M - dM );
% Probability of out of the range
pB ( k ) = sum ( mask ) / nB;
end
В итоге получился такой вот красивый график:

Осмелюсь предположить что 1 млн. коробок мало и если устремить их количество в бесконечность, наши вероятности будут ровно в 90%.
Гораздо интереснее случай, когда аппарат для разлива конфет имеет константное стандартное отклонение, которое больше 1.2285 и нужно найти те самые границы
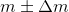 , выше которых, при заданной
, выше которых, при заданной 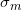 , конфеты нужно отбросить, чтобы удовлетворять тем же условиям. Это куда более сложная задача, которой я возможно посвящу еще одну статью.
, конфеты нужно отбросить, чтобы удовлетворять тем же условиям. Это куда более сложная задача, которой я возможно посвящу еще одну статью.