Введение
Книги и публикации по цифровой обработке сигналов пишут авторы зачастую не догадывающиеся и не понимающие задач, стоящих перед разработчиками. Особенно это касается систем, работающих в реальном времени. Эти авторы отводят себе скромную роль бога, существующего вне времени и пространства, что вызывает некоторое недоумение у читателей подобной литературы. Данная публикация имеет целью развеять недоумения, возникающие у большинства разработчиков, и помочь им преодолеть «порог вхождения», для этих целей в тексте сознательно используется аналогии и терминология сферы программирования.
Данный опус не претендует на полноту и связность изложения.
Добавлено после прочтения комментариев.
Публикаций о том как делать БПФ немеряно, а о том как сделать БПФ, преобразовать спектр, и собрать сигнал заново, да еще и в реальном времени, явно не хватает. Автор пытается восполнить этот пробел.
Часть первая, обзорная
Существуют два основных способа построения дискретных линейных динамических систем. В литературе, такие системы принято называть цифровыми фильтрами, которые подразделяются на два основных типа: фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ).
Алгоритмическая сущность фильтра с КИХ заключается в дискретном вычислении интеграла свертки:

Где x(t) – входной сигнал
y(t) – выходной сигнал
h(t) – импульсная характеристика фильтра или реакция фильтра на дельта функцию. Импульсная характеристика является обратным преобразованием Фурье комплексной частотной характеристики фильтра K(f).
Для формирования ясной картины у читателя, приведем пример дискретного вычисления интеграла свертки на языке С в реальном времени.
Вызывая данную функцию через определенные интервалы времени T и передавая ей в качестве аргумента входной сигнал, на выходе мы получим выходной сигнал, соответствующий реакции фильтра с импульсной характеристикой вида:
h(t)=1 при 0<t<4T,
h(t)=0 в остальных случаях.
Всем собравшимся фильтр с такой импульсной характеристикой более известен под названием «фильтр скользящего среднего», и, соответственно, реализуется он гораздо проще. В данном случае такая импульсная характеристика используется для примера.
Синтезу импульсных характеристик КИХ фильтров посвящена масса литературы, также имеются готовые программные продукты для получения фильтров с заданными свойствами. Автор предпочитает глючный инструмент Filter Design из пакета Matlab, но это дело вкуса.
Используя фильтр с конечной импульсной характеристикой, удается немножечко воспарить над привычной реальностью, так как, в природе не существует динамических систем, имеющих конечную импульсную характеристику. Фильтр КИХ — попытка зайти в частотно-временную область с другого конца, не так как ходит природа, поэтому частотные характеристики этих фильтров зачастую обладают неожиданными свойствами.
Намного ближе к природе фильтры с бесконечной импульсной характеристикой. Алгоритмическая сущность фильтров с бесконечной импульсной характеристикой сводится к рекуррентному (не путать с рекурсивным!) решению дифференциального уравнения, описывающего фильтр. То есть, каждое последующие значение выходного сигнала фильтра вычисляется на основании предыдущего значения. Именно так протекают процессы в реальном мире. Камень, падая с небоскреба каждую секунду, увеличивает свою скорость на 9.8м/с Speed=Speed+9.8, и пройденный путь каждую секунду увеличивается Distance=Distance+Speed. Кто скажет, что это не рекуррентный алгоритм, пусть первый бросит в меня камень. Только в нашей Матрице временной интервал вызова функции возвращающей положение камня много меньше цены деления доступных нам средств измерения.
Отдельно хотелось бы определить понятие «порядок фильтра». Это количество переменных которые подвергаются рекуррентным операциям. В приведенном примере функция, возвращающая скорость камня — первого порядка, функция, возвращающая пройденный путь — второго порядка.
Для окончательного просветления читателя приведем пример на языке С самого простого фильтра низких частот, широко известного как фильтр «фильтр экспоненциального сглаживания»
Вызывая данную функцию с частотой F и передавая ей в качестве аргумента входной сигнал, на выходе мы получим выходной сигнал, соответствующий реакции фильтра низких частот первого порядка с частотой среза:
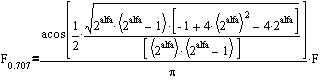
Приведенный пример исходного кода совершенно неудобоварим с точки зрения понимания сути алгоритма. С точки зрения рекуррентной сути (смотри «падение камня» ) алгоритма, правильнее y=y+((x-y)>>alfa);, но в этом случае происходит потеря alfa значащих разрядов. Рекуррентное выражение фильтра, из примера кода, построено таким образом, чтобы избежать потери значащих разрядов. Именно конечная точность вычислений может испортить всю прелесть цифрового фильтра с бесконечной импульсной характеристикой. Особенно это заметно на фильтрах высоких порядков, отличающихся высокой добротностью. В реальных динамических системах такая проблема не возникает, наша Матрица производит вычисления с невероятной для нас точностью.
Синтезу подобных фильтров посвящена масса литературы, также имеются готовые программные продукты (см. выше).
Часть вторая. Фурье – фильтр
Из вузовских курсов (у вашего покорного слуги это был курс ОТЭЦ) многие собравшие помнят два основных подхода к анализу линейных динамических систем: анализ во временной области и анализ в частотной области. Анализ во временной области — это решение дифференциальных уравнений, интегралы свертки и Дюамеля. Эти методы анализа дискретно воплотились в цифровых фильтрах БИХ и КИХ.
Но существует частотный подход к анализу линейных динамических систем. Иногда его называют операторным. В качестве операторов используются преобразование Фурье, Лапласа и т.п. Далее мы будем говорить только о преобразовании Фурье.
Данный метод анализа не получил широкого распространения при построении цифровых фильтров. Автору не удалось найти вменяемых практических рекомендаций по построению подобных фильтров на русском языке. Единственное краткое упоминание такого фильтра в практической литературе [Рабинер Л., Гоулд Б., Теория и применение цифровой обработки сигналов 1978], но в данной книге рассмотрение подобного фильтра очень поверхностно. В указанной книге данная схема построения фильтра называется: «свертка в реальном времени методом БПФ», что, по моему скромному мнению, совершенно не отражает сути, название должно быть коротким, иначе времени на отдых не останется.
Реакция линейной динамической системы есть обратное преобразование Фурье от произведения изображения по Фурье входного сигнала x(t) на комплексный коэффициент передачи K(f):
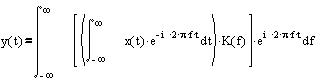
В практическом плане, данное аналитическое выражение предполагает следующий порядок действий: берем преобразование Фурье от входного сигнала, умножаем результат на комплексный коэффициент передачи, выполняем обратное преобразование Фурье, результатом которого является выходной сигнал. В реальном дискретном времени такой порядок действий выполнить невозможно. Как брать интеграл по времени от минус до плюс бесконечности?! Его можно взять только находясь вне времени…
В дискретном мире для выполнения преобразования Фурье существует инструмент — алгоритм быстрого преобразования Фурье (БПФ). Именно его мы и будем использовать при реализации нашего Фурье-фильтра. Аргументом функции БПФ является массив временных отсчетов из 2^n элементов, результатом два массива длинной 2^n элементов соответствующие действительной и мнимой части преобразования Фурье. Дискретной особенностью алгоритма БПФ является то, что входной сигнал считается периодичным с интервалом 2^n. Это накладывает некоторые ограничения на алгоритм Фурье-фильтра. Если взять последовательность выборок входного сигнала, провести от них БПФ, умножить результат БПФ на комплексный коэффициент передачи фильтра и выполнить обратное преобразование …ничего получится! Выходной сигнал будет иметь огромные нелинейные искажения в окрестности стыков выборок.
Для решения этой проблемы необходимо применить два приема:

Такие функции широко применяются в технике цифровой обработки сигналов, и называть их принято — окнами. По скромному мнению автора лучшим, с практической точки зрения, является окно имени Хана:
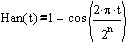
На рисунке приведены графики иллюстрирующие свойства окна Хана длинной 2^n=256. Экземпляры окна построены с половинным перекрытием k=128. Как видно все оговоренные выше свойства имеются в наличии.
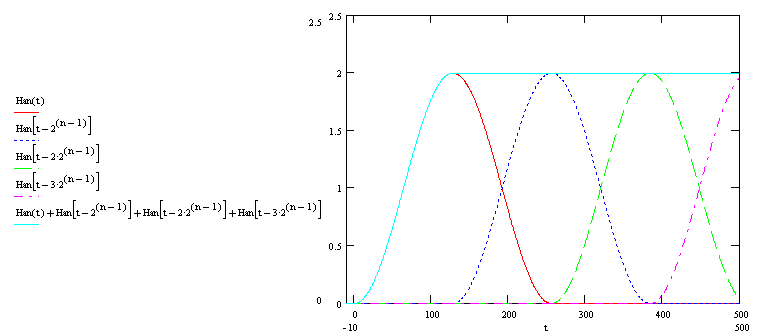
По просьбам трудящихся, на следующем рисунке приведена схема вычислений Фурье-фильтра, при длине выборки 2^n=8, количество выборок 3. На подобных рисунках очень сложно отобразить процесс вычислений, особенно тяжело показать его цикличность, поэтому мы и ограничились количеством выборок равным трем.
Входной сигнал разбивается на блоки длинной 2^n=8 с перекрытием 50%, от каждого блока берется БПФ, результаты БПФ подвергаются нужной трансформации, берется обратное БПФ, результат обратного БПФ скалярно умножается на окно, после умножения блоки складываются с перекрытием.
При выполнение трансформаций спектра, не стоит забывать о главном свойстве массива БПФ действительных сигналов, первая половина массива БПФ комплексно сопряжена со второй половиной, т.е Re[i]=Re[(1<<n)-i]); Im[i]=-Im[(1<<n)-i]);. Если эти требования не выполнить выходной сигнал просто «не соберется».
Теперь мы знаем все, что необходимо для написания алгоритма Фурье-фильтра. Опишем алгоритм на языке С.
Вызывая функцию FureFilter() с частотой FSempl и передавая ей в качестве аргумента входной сигнал, результатом получим выходной сигнал. В данном примере входной сигнал обрабатывается следующим образом: сигнал пропускается через полосовой фильтр с частотами среза FsrLow, FsrHi, подавляются все спектральные составляющие выше и ниже указанных частот, сдвигается спектр сигнала (для звуковых сигналов это воспринимается как эффект Буратино-Карабаса), амплитудный спектр сигнала подвергается сглаживанию фильтром низких частот (для звука это эффект гулкого помещения). Данные действия с сигналом выполнены в качестве примера, для того чтобы показать технические приемы обработки сигнала в частотной области, такие как: соблюдение комплексно-сопряженности коэффициентов, восстановление комплексного спектра по амплитудному, не используя тригонометрических функций и т.п.
Заключение
Стоит отметить, что, скорее всего, данная функция Фурье-фильтра, на практике окажется неработоспособна. При вызове данной функции даже с невысокой частотой 8000Гц, она не успеет выполнится к моменту следующего вызова, не хватить быстродействия. Данный программный код Фурье-фильтра приведен в качестве описания алгоритма, без привязки к конкретным аппаратным ресурсам, и имеет чисто образовательные цели (см. Введение).
При практической реализации следует распараллелить выполнение функции заполнения-опорожнения буфера BufInOut[] (лучше сразу ПДП и т. п.) и функции обработки буфера ObrBuf(), но это уже совсем другая история.
Книги и публикации по цифровой обработке сигналов пишут авторы зачастую не догадывающиеся и не понимающие задач, стоящих перед разработчиками. Особенно это касается систем, работающих в реальном времени. Эти авторы отводят себе скромную роль бога, существующего вне времени и пространства, что вызывает некоторое недоумение у читателей подобной литературы. Данная публикация имеет целью развеять недоумения, возникающие у большинства разработчиков, и помочь им преодолеть «порог вхождения», для этих целей в тексте сознательно используется аналогии и терминология сферы программирования.
Данный опус не претендует на полноту и связность изложения.
Добавлено после прочтения комментариев.
Публикаций о том как делать БПФ немеряно, а о том как сделать БПФ, преобразовать спектр, и собрать сигнал заново, да еще и в реальном времени, явно не хватает. Автор пытается восполнить этот пробел.
Часть первая, обзорная
Существуют два основных способа построения дискретных линейных динамических систем. В литературе, такие системы принято называть цифровыми фильтрами, которые подразделяются на два основных типа: фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ).
Алгоритмическая сущность фильтра с КИХ заключается в дискретном вычислении интеграла свертки:

Где x(t) – входной сигнал
y(t) – выходной сигнал
h(t) – импульсная характеристика фильтра или реакция фильтра на дельта функцию. Импульсная характеристика является обратным преобразованием Фурье комплексной частотной характеристики фильтра K(f).
Для формирования ясной картины у читателя, приведем пример дискретного вычисления интеграла свертки на языке С в реальном времени.
#define L (4) //длинна фильтра
int FIR(int a)
{
static int i=0; //текущая позиция
static int reg[L]; //массив входных значений
static const int h[L]={1,1,1,1};//импульсная характеристика
int b=0;//выходное значение
reg[i]=a; //копируем входное значение в массив входных значений
for(int j=0;j<L;j++)//свертка
{
b=b+h[j]*reg[i];
i=(i-1)&(L-1);
}
i=(i+1)&(L-1);//инкрементируем указатель на следующую позицию
return b;
}Вызывая данную функцию через определенные интервалы времени T и передавая ей в качестве аргумента входной сигнал, на выходе мы получим выходной сигнал, соответствующий реакции фильтра с импульсной характеристикой вида:
h(t)=1 при 0<t<4T,
h(t)=0 в остальных случаях.
Всем собравшимся фильтр с такой импульсной характеристикой более известен под названием «фильтр скользящего среднего», и, соответственно, реализуется он гораздо проще. В данном случае такая импульсная характеристика используется для примера.
Синтезу импульсных характеристик КИХ фильтров посвящена масса литературы, также имеются готовые программные продукты для получения фильтров с заданными свойствами. Автор предпочитает глючный инструмент Filter Design из пакета Matlab, но это дело вкуса.
Используя фильтр с конечной импульсной характеристикой, удается немножечко воспарить над привычной реальностью, так как, в природе не существует динамических систем, имеющих конечную импульсную характеристику. Фильтр КИХ — попытка зайти в частотно-временную область с другого конца, не так как ходит природа, поэтому частотные характеристики этих фильтров зачастую обладают неожиданными свойствами.
Намного ближе к природе фильтры с бесконечной импульсной характеристикой. Алгоритмическая сущность фильтров с бесконечной импульсной характеристикой сводится к рекуррентному (не путать с рекурсивным!) решению дифференциального уравнения, описывающего фильтр. То есть, каждое последующие значение выходного сигнала фильтра вычисляется на основании предыдущего значения. Именно так протекают процессы в реальном мире. Камень, падая с небоскреба каждую секунду, увеличивает свою скорость на 9.8м/с Speed=Speed+9.8, и пройденный путь каждую секунду увеличивается Distance=Distance+Speed. Кто скажет, что это не рекуррентный алгоритм, пусть первый бросит в меня камень. Только в нашей Матрице временной интервал вызова функции возвращающей положение камня много меньше цены деления доступных нам средств измерения.
Отдельно хотелось бы определить понятие «порядок фильтра». Это количество переменных которые подвергаются рекуррентным операциям. В приведенном примере функция, возвращающая скорость камня — первого порядка, функция, возвращающая пройденный путь — второго порядка.
Для окончательного просветления читателя приведем пример на языке С самого простого фильтра низких частот, широко известного как фильтр «фильтр экспоненциального сглаживания»
#define alfa (2) //параметр сглаживания
int filter(int a)
{
static int out_alfa=0;
out_alfa=out_alfa - (out_alfa >>alfa) + a;
return (out_alfa >> alfa);
}Вызывая данную функцию с частотой F и передавая ей в качестве аргумента входной сигнал, на выходе мы получим выходной сигнал, соответствующий реакции фильтра низких частот первого порядка с частотой среза:

Приведенный пример исходного кода совершенно неудобоварим с точки зрения понимания сути алгоритма. С точки зрения рекуррентной сути (смотри «падение камня» ) алгоритма, правильнее y=y+((x-y)>>alfa);, но в этом случае происходит потеря alfa значащих разрядов. Рекуррентное выражение фильтра, из примера кода, построено таким образом, чтобы избежать потери значащих разрядов. Именно конечная точность вычислений может испортить всю прелесть цифрового фильтра с бесконечной импульсной характеристикой. Особенно это заметно на фильтрах высоких порядков, отличающихся высокой добротностью. В реальных динамических системах такая проблема не возникает, наша Матрица производит вычисления с невероятной для нас точностью.
Синтезу подобных фильтров посвящена масса литературы, также имеются готовые программные продукты (см. выше).
Часть вторая. Фурье – фильтр
Из вузовских курсов (у вашего покорного слуги это был курс ОТЭЦ) многие собравшие помнят два основных подхода к анализу линейных динамических систем: анализ во временной области и анализ в частотной области. Анализ во временной области — это решение дифференциальных уравнений, интегралы свертки и Дюамеля. Эти методы анализа дискретно воплотились в цифровых фильтрах БИХ и КИХ.
Но существует частотный подход к анализу линейных динамических систем. Иногда его называют операторным. В качестве операторов используются преобразование Фурье, Лапласа и т.п. Далее мы будем говорить только о преобразовании Фурье.
Данный метод анализа не получил широкого распространения при построении цифровых фильтров. Автору не удалось найти вменяемых практических рекомендаций по построению подобных фильтров на русском языке. Единственное краткое упоминание такого фильтра в практической литературе [Рабинер Л., Гоулд Б., Теория и применение цифровой обработки сигналов 1978], но в данной книге рассмотрение подобного фильтра очень поверхностно. В указанной книге данная схема построения фильтра называется: «свертка в реальном времени методом БПФ», что, по моему скромному мнению, совершенно не отражает сути, название должно быть коротким, иначе времени на отдых не останется.
Реакция линейной динамической системы есть обратное преобразование Фурье от произведения изображения по Фурье входного сигнала x(t) на комплексный коэффициент передачи K(f):
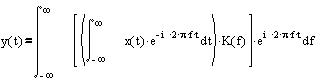
В практическом плане, данное аналитическое выражение предполагает следующий порядок действий: берем преобразование Фурье от входного сигнала, умножаем результат на комплексный коэффициент передачи, выполняем обратное преобразование Фурье, результатом которого является выходной сигнал. В реальном дискретном времени такой порядок действий выполнить невозможно. Как брать интеграл по времени от минус до плюс бесконечности?! Его можно взять только находясь вне времени…
В дискретном мире для выполнения преобразования Фурье существует инструмент — алгоритм быстрого преобразования Фурье (БПФ). Именно его мы и будем использовать при реализации нашего Фурье-фильтра. Аргументом функции БПФ является массив временных отсчетов из 2^n элементов, результатом два массива длинной 2^n элементов соответствующие действительной и мнимой части преобразования Фурье. Дискретной особенностью алгоритма БПФ является то, что входной сигнал считается периодичным с интервалом 2^n. Это накладывает некоторые ограничения на алгоритм Фурье-фильтра. Если взять последовательность выборок входного сигнала, провести от них БПФ, умножить результат БПФ на комплексный коэффициент передачи фильтра и выполнить обратное преобразование …ничего получится! Выходной сигнал будет иметь огромные нелинейные искажения в окрестности стыков выборок.
Для решения этой проблемы необходимо применить два приема:
- 1. Выборки необходимо обрабатывать преобразованием Фурье с перекрытием. То есть, каждая последующая выборка должно содержать часть предыдущей. В идеальном случае выборки должны перекрываться на (2^n-1) отсчетов, но это требует огромных вычислительных затрат. На практике, с лихвой, достаточно трехчетвертного (2^n-2^(n-2)), половинного (2^(n-1)) и даже четвертного перекрытия (2^(n-2)).
- 2. Результаты обратного преобразования Фурье, для получения выходного сигнала, необходимо, перед наложение друг на друга, умножить на весовую функцию (массив весовых коэффициентов). Весовая функция должна удовлетворять следующим условиям:
- 2.1 Равна нулю везде, кроме интервала 2^n.
- 2.2 На краях интервала стремится к нулю.
- 2.3 И, самое главное, сумма весовых функций Fv(t), сдвинутых на интервал перекрытия k должна быть постоянна:

Такие функции широко применяются в технике цифровой обработки сигналов, и называть их принято — окнами. По скромному мнению автора лучшим, с практической точки зрения, является окно имени Хана:
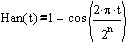
На рисунке приведены графики иллюстрирующие свойства окна Хана длинной 2^n=256. Экземпляры окна построены с половинным перекрытием k=128. Как видно все оговоренные выше свойства имеются в наличии.

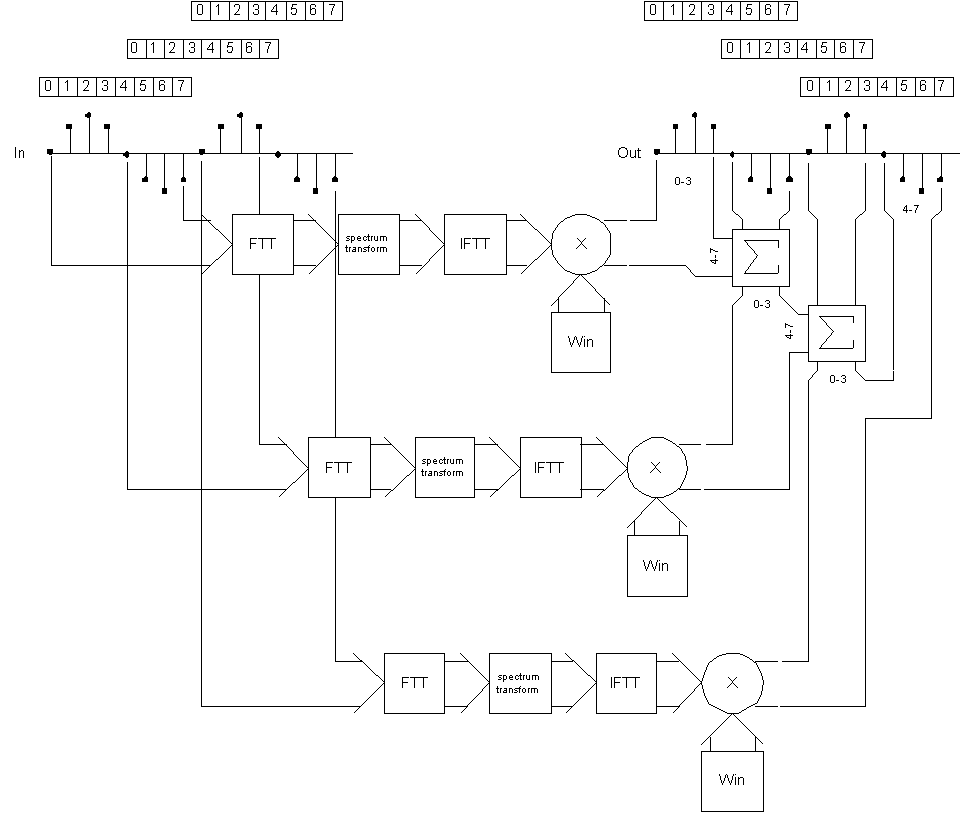
По просьбам трудящихся, на следующем рисунке приведена схема вычислений Фурье-фильтра, при длине выборки 2^n=8, количество выборок 3. На подобных рисунках очень сложно отобразить процесс вычислений, особенно тяжело показать его цикличность, поэтому мы и ограничились количеством выборок равным трем.

Входной сигнал разбивается на блоки длинной 2^n=8 с перекрытием 50%, от каждого блока берется БПФ, результаты БПФ подвергаются нужной трансформации, берется обратное БПФ, результат обратного БПФ скалярно умножается на окно, после умножения блоки складываются с перекрытием.
При выполнение трансформаций спектра, не стоит забывать о главном свойстве массива БПФ действительных сигналов, первая половина массива БПФ комплексно сопряжена со второй половиной, т.е Re[i]=Re[(1<<n)-i]); Im[i]=-Im[(1<<n)-i]);. Если эти требования не выполнить выходной сигнал просто «не соберется».
Теперь мы знаем все, что необходимо для написания алгоритма Фурье-фильтра. Опишем алгоритм на языке С.
#include <math.h>
#define FSempl (8000)//частота семплирования Гц
#define BufL (64) //длинна буфера обработки
#define Perk (2) //перекрытие кадров 2-1/2, 4-3/4
//ограничение спектра, полосовой фильтр
#define FsrLow (300)//нижняя частота фильтра Гц
#define FsrHi (3100)//верхняя частота фильтра Гц
#define FsrLowN ((BufL*FsrLow+(FSempl/2))/FSempl)//нижняя частота в гармониках
#define FsrHiN ((BufL*FsrHi +(FSempl/2))/FSempl)//верхняя частота в гармониках
//Сдвиг спектра
#define SdvigSp (0)//сдвиг спектра в гармониках +(вниз) -(вверх) 0(без сдвига)
//Фильтр спектра во времени, эхо
#define FilterSpekrtaT_EN (1)//использовать фильтр спектра 1/0
#define FiltSpektrFsr (0.100025f) //частота среза фильтра спектра
volatile unsigned short ShBuf;//счетчик входного буфера
signed short BufIn[BufL*2];//входной буфер
signed short BufOut[BufL*2];//выходной буфер
signed short BufInOut[BufL];//буфер для перезаписи
float FurRe[BufL];//Фурье действительная часть
float FurIm[BufL];//Фурье мнимая часть
#if (FilterSpekrtaT_EN!=0)
float FStektr[BufL/2];//фильтр амплитудного спектра
#endif
//Таблица синуса косинуса
#if BufL==64
const float SinCosF[]=
{
0.000000000 , 0.098017140 , 0.195090322 , 0.290284677 ,
0.382683432 , 0.471396737 , 0.555570233 , 0.634393284 ,
0.707106781 , 0.773010453 , 0.831469612 , 0.881921264 ,
0.923879533 , 0.956940336 , 0.980785280 , 0.995184727 ,
1.000000000 , 0.995184727 , 0.980785280 , 0.956940336 ,
0.923879533 , 0.881921264 , 0.831469612 , 0.773010453 ,
0.707106781 , 0.634393284 , 0.555570233 , 0.471396737 ,
0.382683432 , 0.290284677 , 0.195090322 , 0.098017140 ,
0.000000000 , -0.098017140, -0.195090322, -0.290284677,
-0.382683432, -0.471396737, -0.555570233, -0.634393284,
-0.707106781, -0.773010453, -0.831469612, -0.881921264,
-0.923879533, -0.956940336, -0.980785280, -0.995184727,
-1.000000000, -0.995184727, -0.980785280, -0.956940336,
-0.923879533, -0.881921264, -0.831469612, -0.773010453,
-0.707106781, -0.634393284, -0.555570233, -0.471396737,
-0.382683432, -0.290284677, -0.195090322, -0.098017140,
0.000000000 , 0.098017140 , 0.195090322 , 0.290284677 ,
0.382683432 , 0.471396737 , 0.555570233 , 0.634393284 ,
0.707106781 , 0.773010453 , 0.831469612 , 0.881921264 ,
0.923879533 , 0.956940336 , 0.980785280 , 0.995184727
};
#endif
//таблица сортировки БПФ
#if BufL==64
const unsigned short sortFFT[]=
{
0x0000,0x0020,0x0010,0x0030,0x0008,0x0028,0x0018,0x0038,
0x0004,0x0024,0x0014,0x0034,0x000C,0x002C,0x001C,0x003C,
0x0002,0x0022,0x0012,0x0032,0x000A,0x002A,0x001A,0x003A,
0x0006,0x0026,0x0016,0x0036,0x000E,0x002E,0x001E,0x003E,
0x0001,0x0021,0x0011,0x0031,0x0009,0x0029,0x0019,0x0039,
0x0005,0x0025,0x0015,0x0035,0x000D,0x002D,0x001D,0x003D,
0x0003,0x0023,0x0013,0x0033,0x000B,0x002B,0x001B,0x003B,
0x0007,0x0027,0x0017,0x0037,0x000F,0x002F,0x001F,0x003F
};
#endif
//Таблица окно Хана
#if BufL==64
const float WinHanF[]=
{
0.0 , 0.002407637 , 0.00960736 , 0.021529832 ,
0.038060234 , 0.059039368 , 0.084265194 , 0.113494773 ,
0.146446609 , 0.182803358 , 0.222214883 , 0.264301632 ,
0.308658284 , 0.354857661 , 0.402454839 , 0.45099143 ,
0.5 , 0.54900857 , 0.597545161 , 0.645142339 ,
0.691341716 , 0.735698368 , 0.777785117 , 0.817196642 ,
0.853553391 , 0.886505227 , 0.915734806 , 0.940960632 ,
0.961939766 , 0.978470168 , 0.99039264 , 0.997592363 ,
1.0 , 0.997592363 , 0.99039264 , 0.978470168 ,
0.961939766 , 0.940960632 , 0.915734806 , 0.886505227 ,
0.853553391 , 0.817196642 , 0.777785117 , 0.735698368 ,
0.691341716 , 0.645142339 , 0.597545161 , 0.54900857 ,
0.5 , 0.45099143 , 0.402454839 , 0.354857661 ,
0.308658284 , 0.264301632 , 0.222214883 , 0.182803358 ,
0.146446609 , 0.113494773 , 0.084265194 , 0.059039368 ,
0.038060234 , 0.021529832 , 0.00960736 , 0.002407637
};
#endif
//@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
//Вычисление прямого Быстрого Преобразования Фурье
//аргументы
//указатель на массив для действительной ReFT и мнимой части ImFT
//После выполнения массивы содержат коэф. действительной и мнимой части
void FFTnoInv(float* ReFT,float* ImFT)
{
//копирование и перестановка
for(int i=0;i<BufL;i++)
{
int j=sortFFT[i];//реверс битов
if(i<j)//проверка на уже переставленные
{
//собственно перестановка
float swp=ReFT[i];
ReFT[i]=ReFT[j];
ReFT[j]=swp;
//нет необходимости для действительных сигналов
//swp=ImFT[i];
//ImFT[i]=ImFT[j];
//ImFT[j]=swp;
}
}
//БПФ
long darg=BufL; //приращение аргумента ядра
for(long LP2=1;LP2!=BufL;LP2=LP2<<1)//проходы
{
darg=darg>>1;
long arg=0; //аргумент ядра, фаза
for(int j=0;j<LP2;j++) //одинаковые группы бабочек
{
float c=(SinCosF[arg+(BufL/4)]);//косинус
float s=(SinCosF[arg]);//синус
arg=(arg-darg)&(BufL-1);//приращение аргумента
for(int i=j;i<BufL;i=(i+LP2+LP2)) //одинаковые бабочки
{
//бабочка!!!
float wr=(c*ReFT[i+LP2])-(s*ImFT[i+LP2]);
float wi=(s*ReFT[i+LP2])+(c*ImFT[i+LP2]);
ReFT[i+LP2]=ReFT[i]-wr;
ImFT[i+LP2]=ImFT[i]-wi;
ReFT[ i ]=ReFT[i]+wr;
ImFT[ i ]=ImFT[i]+wi;
}
}
}
//конец
return;
}
//@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
//Вычисление обратного Быстрого Преобразования Фурье
//аргументы
//указатель на массив для действительной ReFT и мнимой части ImFT
//После выполнения массивы содержат коэф. действительной и мнимой части
//для обычных сигналов мнимая часть равна 0
void FFTInv(float* ReFT,float* ImFT)
{
//копирование и перестановка
for(int i=0;i<BufL;i++)
{
int j=sortFFT[i];//реверс
if(i<j)//проверка на уже переставленные
{
//собственно перестановка
float swp=ReFT[i];
ReFT[i]=ReFT[j];
ReFT[j]=swp;
swp=ImFT[i];
ImFT[i]=ImFT[j];
ImFT[j]=swp;
}
}
//БПФ
long darg=BufL;//приращение аргумента ядра
for(long LP2=1;LP2!=BufL;LP2=LP2<<1)//проходы
{
darg=darg>>1;
long arg=0;////аргумент ядра, фаза
for(int j=0;j<LP2;j++)//группы бабочек
{
float c=(SinCosF[arg+(BufL/4)]);//косинус
float s=(SinCosF[arg]);//синус
arg=arg+darg;//приращение аргумента
for(int i=j;i<BufL;i=(i+LP2+LP2))//одинаковые бабочки
{
//бабочка!!!
float wr=(c*ReFT[i+LP2])-(s*ImFT[i+LP2]);
float wi=(s*ReFT[i+LP2])+(c*ImFT[i+LP2]);
ReFT[i+LP2]=ReFT[i]-wr;
ImFT[i+LP2]=ImFT[i]-wi;
ReFT[ i ]=ReFT[i]+wr;
ImFT[ i ]=ImFT[i]+wi;
}
}
}
//нормировка, применяем окно
for(int i=0;i<BufL;i++)
{
ReFT[i]=ReFT[i]
*
WinHanF[i]
*
(
(1.0F/((float)BufL))
*
(2.0F/((float)Perk))
);
}
//конец
return;
}
//@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
//обработка буферов
void ObrBuf(void)
{
//загружаем Фурье преобразователь
for(int i=0;i<(BufL);i++)
{
FurRe[i]=((float)BufInOut[i]);
FurIm[i]=0.0F;
}
//выполняем прямое преобразование
FFTnoInv(FurRe,FurIm);
//сдвиг спектра
#if SdvigSp>0
//сдвиг спектра вниз, Карабас-Барабас
for(int i=1;i<(BufL/2);i++)
{
if(i>=(BufL/2-SdvigSp))
{
FurRe[i]=FurIm[i]=0;
FurRe[BufL-i]=FurIm[BufL-i]=0;
continue;
}
FurRe[i]=FurRe[i+SdvigSp];
FurIm[i]=FurIm[i+SdvigSp];
FurRe[BufL-i]=FurRe[i];
FurIm[BufL-i]=-FurIm[i];
}
#endif
#if SdvigSp<0
//сдвиг спектра вверх, Буратино
for(int i=(BufL/2-1);i>0;i--)
{
if(i<=(-SdvigSp))
{
FurRe[i]=FurIm[i]=0;
FurRe[BufL-i]=FurIm[BufL-i]=0;
continue;
}
FurRe[i]=FurRe[i-(-SdvigSp)];
FurIm[i]=FurIm[i-(-SdvigSp)];
FurRe[BufL-i]=FurRe[i];
FurIm[BufL-i]=-FurIm[i];
}
#endif
//обрезание спектра, полосовой фильтр
FurRe[0]=0.0F;FurIm[0]=0.0F; //постоянная составляющая
FurRe[(BufL/2)]=0.0F;FurIm[(BufL/2)]=0.0F;//последняя гармоника
float ZnStektr[BufL/2];//амплитудный спектр кадра
for(int i=1;i<(BufL/2);i++)
{
if(
( i < FsrLowN )//нижняя частота
||
( i > FsrHiN )//верхняя частота
)
{
//обрезание спектра, гармоники вне полосы зануляем
FurRe[i]=0.0F;FurIm[i]=0.0F;//прямые гармоники
FurRe[BufL-i]=0.0F;FurIm[BufL-i]=0.0F;//сопряженные гармоники
}
else //считаем амплитудный спектр не обрезанной части
{
ZnStektr[i]=sqrtf(FurRe[i]*FurRe[i])+(FurIm[i]*FurIm[i]);//амплитудный спектр
}
}
//фильтр амплитудного спектра во времени, эхо
for(int i= FsrLowN;//нижняя частота
i<=FsrHiN ;//верхняя частота
i++)
{
#if FilterSpekrtaT_EN!=0
//фильтр спектра во времени, эхо
FStektr[i]=FStektr[i]+ FiltSpektrFsr*(ZnStektr[i]-FStektr[i]);
#endif
//переходим от модуля к комплексному числу
FurRe[i]=FurRe[BufL-i]=(FStektr[i]*FurRe[i])/ZnStektr[i];
FurIm[i]=(FStektr[i]*FurIm[i])/ZnStektr[i];
FurIm[BufL-i]=-FurIm[i];
}
//выполняем обратное БПФ
FFTInv(FurRe,FurIm);
//копирование буферов
for(int i=0;i<(BufL);i++)
{
BufInOut[i]=((signed short)(FurRe[i]+0.5f));
}
}
//@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
//Фурье фильтр
signed short FureFilter(signed short t1)
{
//записываем во входной буфер
BufIn[ShBuf]=t1;
//выходное значение
signed short out=BufOut[ShBuf];
//инкремент указателя буфера
ShBuf=(ShBuf+1)&((BufL*2)-1);
//если в буфере часть кадра обработки
if((ShBuf&((BufL/Perk)-1))==0)
{
//переписываем буфер обработки в выходной буфер
int ShTmpOut=ShBuf;
int ShTmpIn=(ShBuf-BufL)&((BufL*2)-1);
for(int i=0;i<(BufL);i++)
{
if(i<(BufL-(BufL/Perk)))
{
//переписываем первую часть буфера обработки в выходной буфер
BufOut[ShTmpOut]=BufOut[ShTmpOut]+BufInOut[i];
}
else
{ //переписываем вторую часть буфера обработки в выходной буфер
BufOut[ShTmpOut]=BufInOut[i];
}
//инкремент указателя выходного буфера
ShTmpOut=(ShTmpOut+1)&((BufL*2)-1);
//переписываем входной буфер в буфер обработки
BufInOut[i]=BufIn[ShTmpIn];
//инкремент указателя входного буфера
ShTmpIn=(ShTmpIn+1)&((BufL*2)-1);
}
}//конец if((ShBuf&((BufL/Perk)-1))==0)
//вызов функции обработки
//в на реальном процессоре распараллелить!
if((ShBuf&((BufL/Perk)-1))==0)ObrBuf();
return out;
}Вызывая функцию FureFilter() с частотой FSempl и передавая ей в качестве аргумента входной сигнал, результатом получим выходной сигнал. В данном примере входной сигнал обрабатывается следующим образом: сигнал пропускается через полосовой фильтр с частотами среза FsrLow, FsrHi, подавляются все спектральные составляющие выше и ниже указанных частот, сдвигается спектр сигнала (для звуковых сигналов это воспринимается как эффект Буратино-Карабаса), амплитудный спектр сигнала подвергается сглаживанию фильтром низких частот (для звука это эффект гулкого помещения). Данные действия с сигналом выполнены в качестве примера, для того чтобы показать технические приемы обработки сигнала в частотной области, такие как: соблюдение комплексно-сопряженности коэффициентов, восстановление комплексного спектра по амплитудному, не используя тригонометрических функций и т.п.
Заключение
Стоит отметить, что, скорее всего, данная функция Фурье-фильтра, на практике окажется неработоспособна. При вызове данной функции даже с невысокой частотой 8000Гц, она не успеет выполнится к моменту следующего вызова, не хватить быстродействия. Данный программный код Фурье-фильтра приведен в качестве описания алгоритма, без привязки к конкретным аппаратным ресурсам, и имеет чисто образовательные цели (см. Введение).
При практической реализации следует распараллелить выполнение функции заполнения-опорожнения буфера BufInOut[] (лучше сразу ПДП и т. п.) и функции обработки буфера ObrBuf(), но это уже совсем другая история.