Многие из нас в школе или университете посещали уроки черчения, но не многим из нас это нравилось. Часами возиться с линейкой, циркулем и плохо заточенным карандашом, пытаясь ровно и без помарок выводить размерные линии, бесконечные штриховки и странные формы, мало кому могло показаться интересным. Тем более, что к тому времени уже существовали компьютерные программы, способные автоматизировать это скучное, бессмысленное и беспощадное занятие. А настоящий прорыв в области проектирования деталей и подготовки конструкторской документации произошел в 1989 вместе с дебютом параметрического моделирования в Системе Автоматизированного Проектирования (САПР) Pro/Engineer.
Это — вводная статья к циклу статей "Параметрическое моделирование". Из этого цикла вы узнаете о внутреннем устройстве настоящего решателя геометрических ограничений, проблемах и их решениях на примере open-source САПР "SolveSpace". Кому не чужд мир трехмерного моделирования, добро пожаловать под кат!
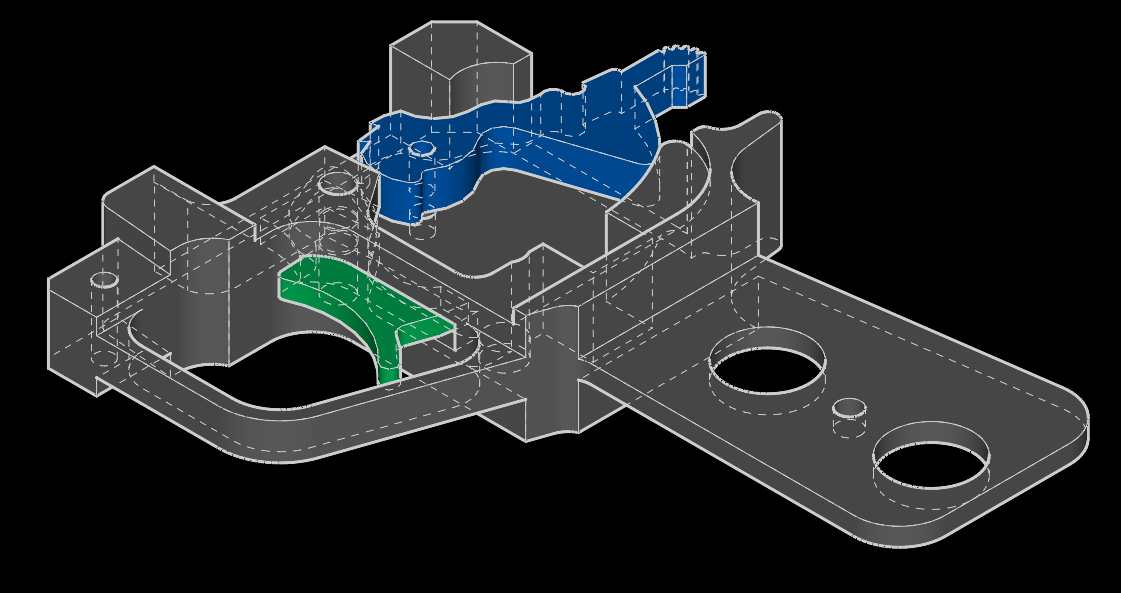
Модель ударно-спускового механизма РПГ-7, созданная в САПР SolveSpace
Идея
В основе параметрического моделирования лежит простая идея: выразить сложные геометрические формы изделий с помощью простых примитивов (entities), форма которых задается с помощью параметров (parameters) и отношений между ними. Параметрами могут быть координаты точек, величины углов, длин, радиусов окружностей или эллипсов. Отношения между параметрами называют ограничениями (constraints). Для инженера-конструктора такие ограничения выглядят как размеры или как геометрические отношения инцидентности (совпадения), параллельности, перпендикулярности или касательности простейших геометрических форм: точек, линий, окружностей, эллипсов и т. д. Совокупность примитивов, служащих основой для построения геометрического представления детали, называют эскизом (sketch). При таком подходе процесс построения эскиза сводится к формированию грубого наброска контура объектов и наложению таких ограничений, которые однозначно определяют значения параметров всех примитивов. Преимуществом такого подхода является то, что инженеру не требуется точно определять координаты всех объектов, достаточно указать лишь геометрические взаимоотношения между объектами, а всю работу по вычислению результирующих координат объектов выполнит решатель геометрических ограничений (geometric constraint solver) — основа параметрического подхода к моделированию. Именно наличие такого решателя отличает параметрические САПР от остальных.
SolveSpace
Подробности реализации системы параметрического моделирования будем рассматривать на основе open-source проекта SolveSpace, созданного Джонатаном Вэстью (Jonathan Westhues) и поддерживаемого в настоящее время сообществом open-source — разработчиков, в числе которых состоит и автор данной статьи, то есть я.
Среди всех проектов с открытым исходным кодом, SolveSpace обладает самой адекватной реализацией решателя геометрических ограничений. Решатель SolveSpace имеет си-подобный интерфейс и доступен для лицензирования и использования в коммерческих проектах. Основным преимуществом решателя, созданного Джонатаном, является символьный подход к записи исходных уравнений, что позволяет очень быстро и просто создавать новые ограничения, а также предоставляет возможность вычислять выражения в полях ввода значений. Еще одним преимуществом решателя SolveSpace является возможность единообразно решать как двумерные, так и трехмерные ограничения.
В качестве контр-примера можно привести встроенный решатель FreeCAD, который построен на других принципах, что вызывает ряд проблем. Одной из проблем является сложность добавления новых ограничений ввиду того, что приходится вручную записывать все частные производные уравнений. Но основным минусом решателя FreeCAD является его ограниченность областью проектирования двумерных эскизов, что негативным образом сказалось на функциональности FreeCAD — в нем до сих пор нет нормальной возможности делать трехмерные сборки деталей.
Эскиз (Sketch)
Несмотря на то, что SolveSpace является параметрической системой трехмерного моделирования, объемные тела создаются на основе набора двумерных контуров. Контуры в SolveSpace могут состоять из отрезков прямых, окружностей и их дуг, а также кубических сплайнов. Иерархически вложенные контуры становятся "дырками", а контуры, вложенные в “дырки” — снова становятся частью тел.
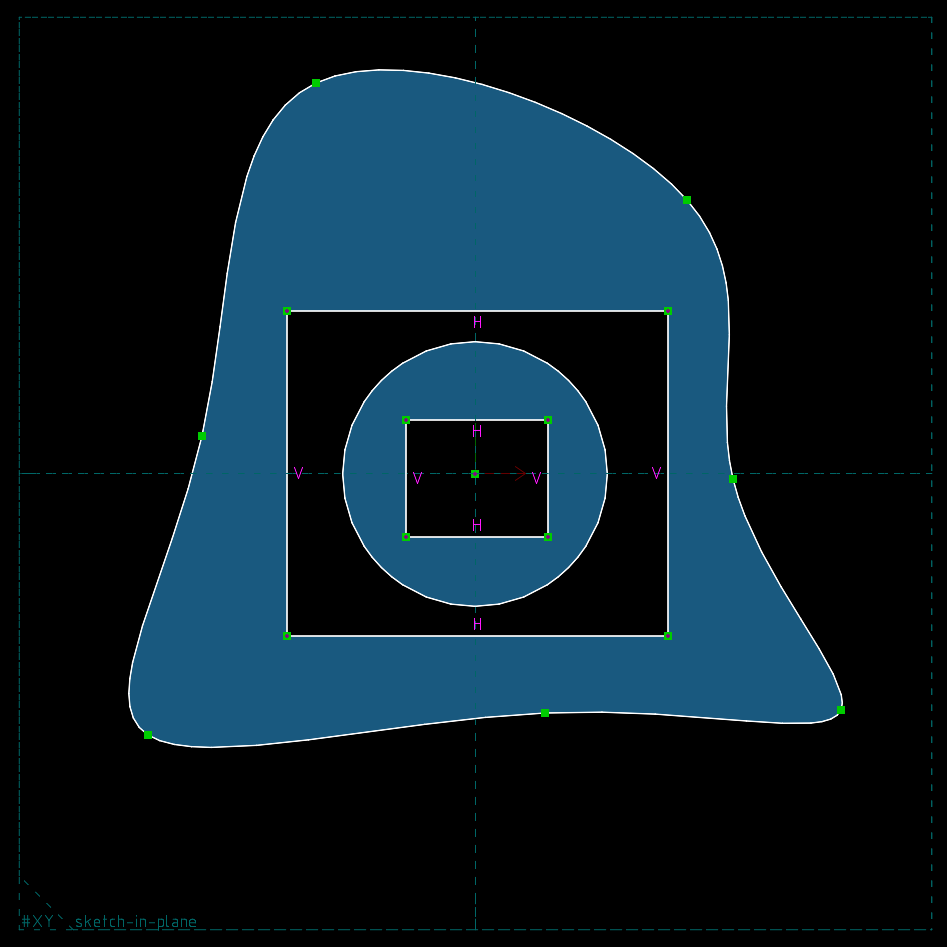
Пример эскиза
В SolveSpace возможно создание тел выдавливания (extrusion) и тел вращения (lathe), а все остальные тела можно получить объединением этих двух типов с использованием так называемых Булевых (Boolean) операций, которые являются основой Constructive Solid Geometry(CSG).
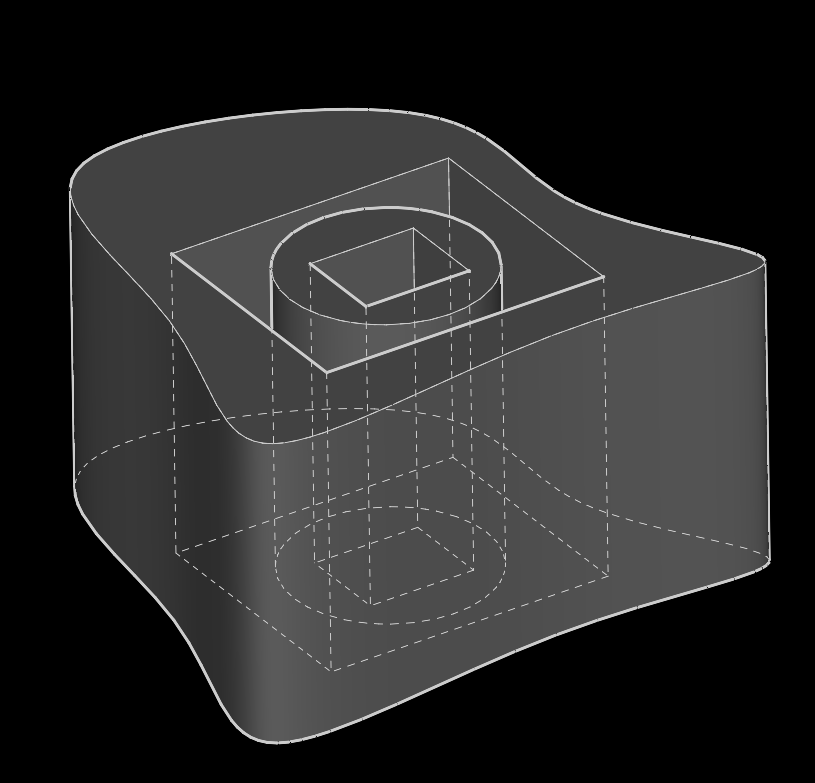
Пример тела выдавливания (extrusion)
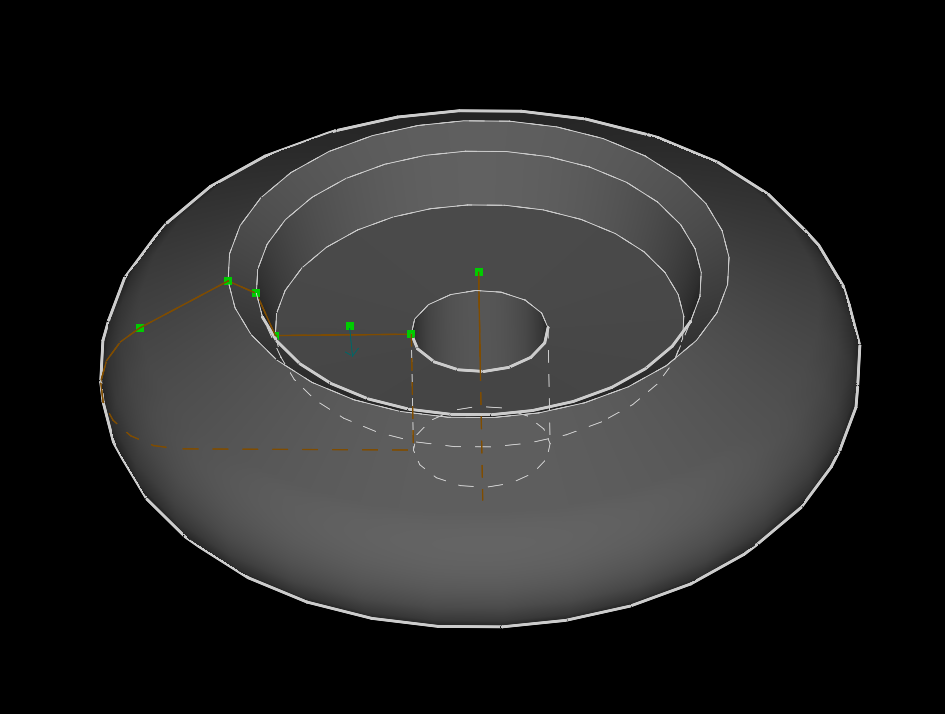
Пример тела вращения (revolution, lathe)
Ограничения (Constraints)
Ограничения в параметрических САПР отличаются от размерных линий обыкновенных систем автоматизированного проектирования. Их основное отличие состоит в том, что изменение размерного значения меняет и сам эскиз, то есть ограничения предоставляют интерфейс двустороннего взаимодействия. Ограничения могут "измерять" размеры эскиза, то есть выполнять роль размеров “для справок” (reference). С другой стороны, ограничения могут изменять сам эскиз при изменении значения параметра ограничения. Это очень удобно, так как во множестве случаев инженеру-конструктору требуется создать документацию не единичного изделия, а целого семейства изделий, обладающих сходной формой, но различными значениями ряда размеров. К примеру, это могут быть обыкновенные гайки:
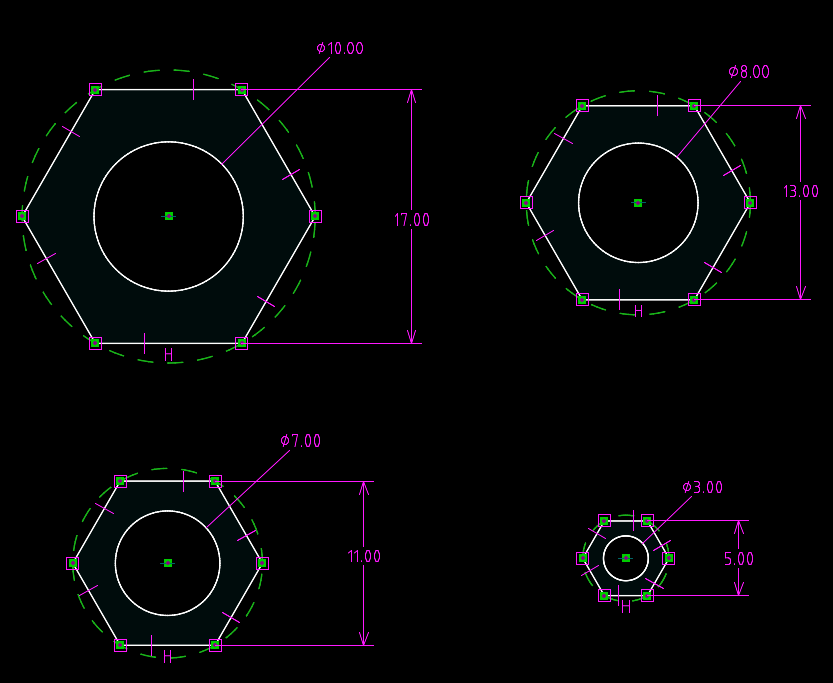
Эскизы гаек различного размера
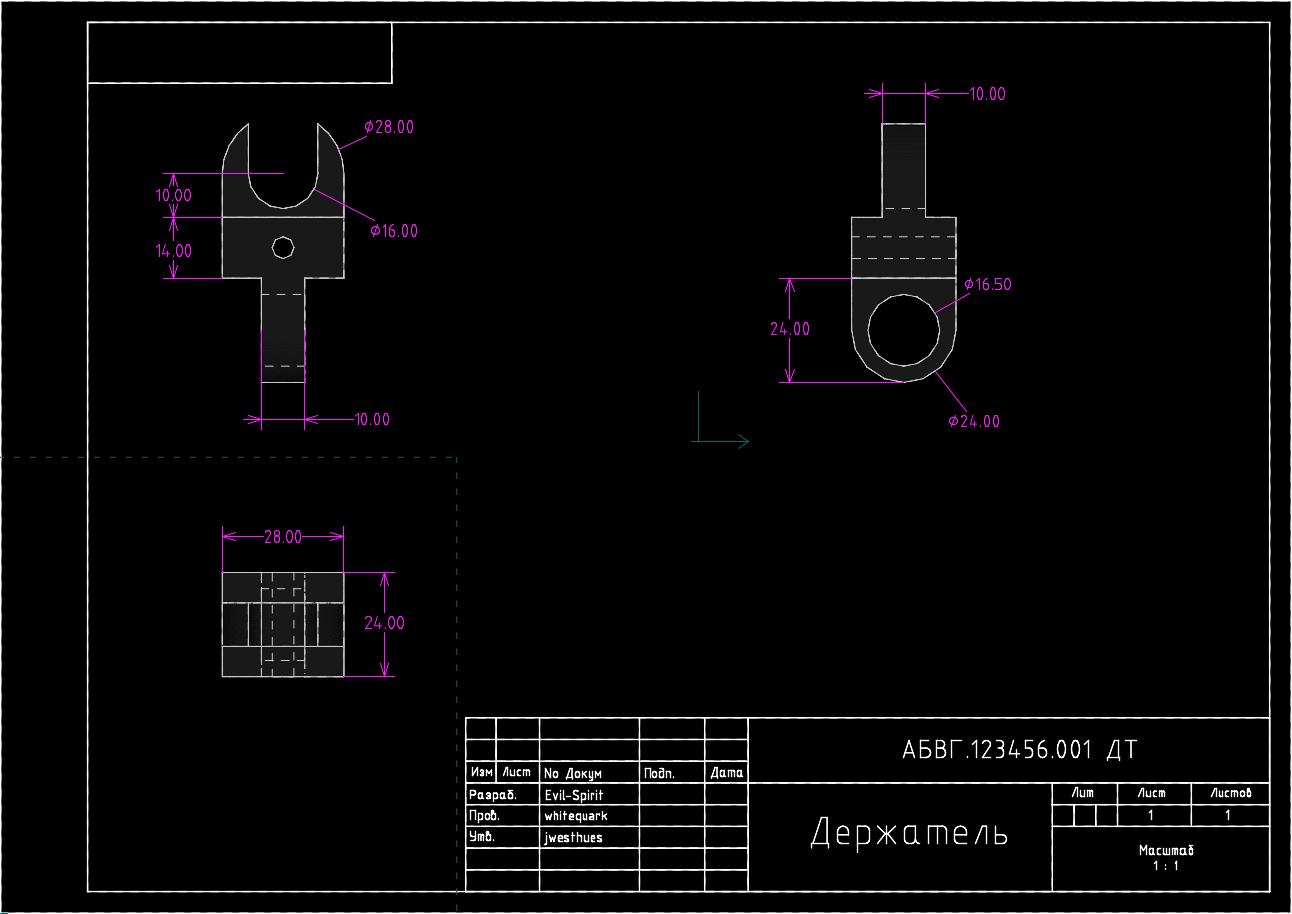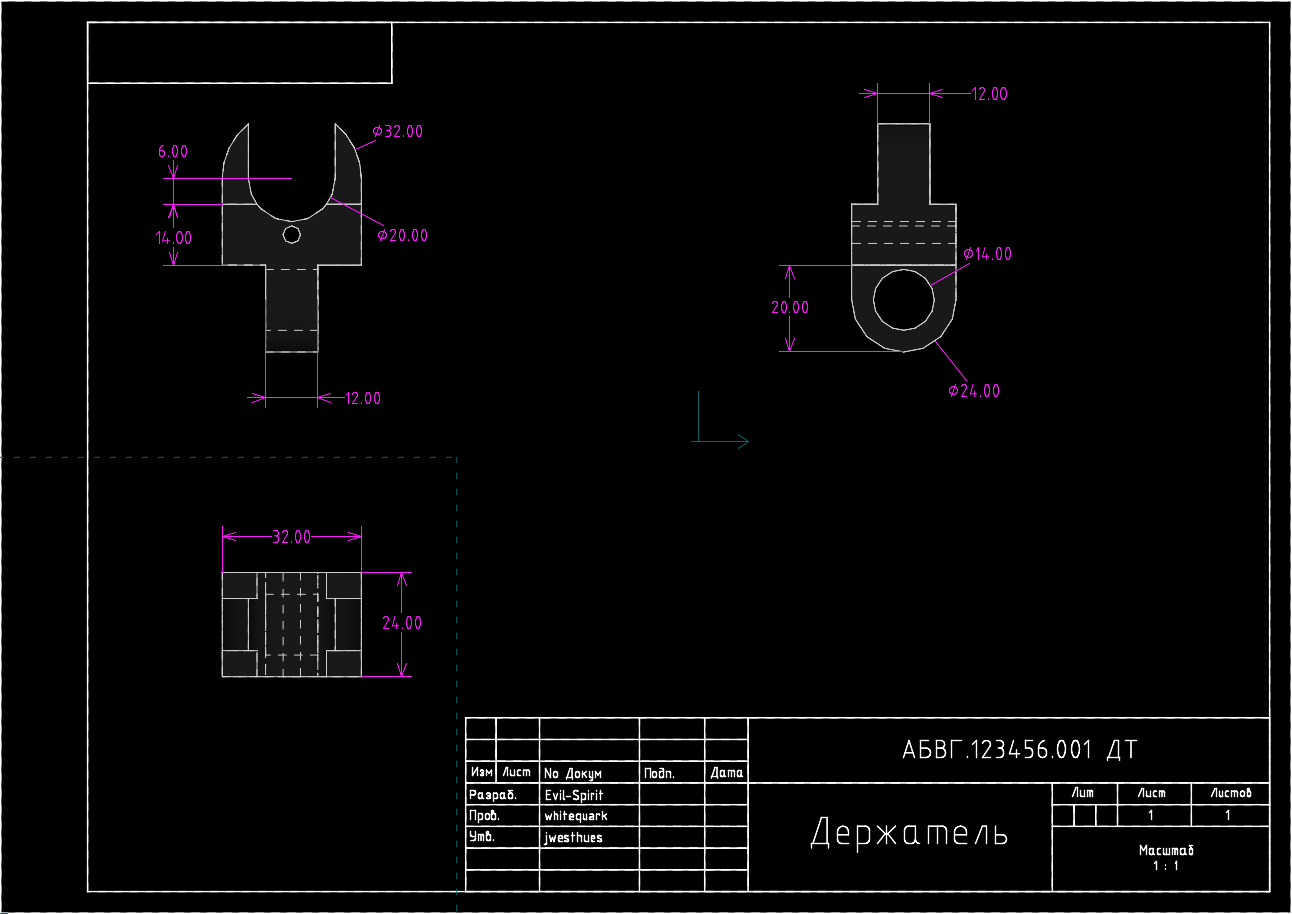
Автоматическая перестройка чертежа при изменении некоторых параметров детали
В этом и состоит мощь параметрического моделирования: изменяя всего один или несколько параметров мы добиваемся полной перестройки всей модели, включая трехмерное представление и наборы видов на каждом из чертежей. Не нужно вносить тысячи правок, если необходимо изменить всего один размер — достаточно задать его новое значение и решатель геометрических ограничений рассчитает новые координаты объектов, а в случае ввода некорректных значений выдаст сообщение об ошибке.
Часть 1: Введение
Часть 2: Эскиз
Часть 3: Степени свободы и уравнения ограничений
Часть 4: «Неисповедимы пути Решателя» или «Червоточины Ньютона»