→ Это предыстория и продолжение статьи:
Дело было вечером…все статьи на Хабре были прочитаны, затеял «небольшой» проект по автономной ориентации робота на RaspberryPi 3. С железом проблем нет, собирается недорого из г-на и палок купленных на ебау деталек, камера с хорошей стеклянной оптикой (это важно для стабильности калибраций), привод камеры вверх, вниз и компас, гироскоп и тд прикрепленные к камере:

Существующие системы SLAM не устраивают, или по цене, или по качеству/скорости. Поскольку наработок деталей для Visual SLAM у меня много, решил шаг за шагом писать и выкладывать алгоритмы и код в открытый доступ, с обоснованием причин выбора тех или иных алгоритмов.
В целом план следующий (всё на C++, кроме последнего):
Выделение особых точек и их регистрация это критический шаг и по производительности и по аккуратности.Существующие (известные мне) алгоритмы не подходят (для данной платформы), или по скорости, или по аккуратности (precision).
У алгоритмов связывания (matching) точек есть 3 характеристики:
Поскольку связанные точки используются в дальнейшем для нахождения матрицы трансформации при помощи RANSAC метода сложность которого ~O((1/precision)^N) где N — минимальное число пар связанных точек необходимое для вычисления данной матрицы. Если вы ищите плоскость (homography matrix) в 3D (спроецированную в 2D), то N=4, если жесткую трансформацию 3D точек (fundamental matrix), то N=5-8. То есть если, например, precision = 0.1(10%), то для поиска homography вам потребуется десятки тысяч недешевых проб, а для fundamental миллионы. Поэтому был разработан и протестирован алгоритм с высоким precision.
Для проверок алгоритмов детектирования и связывания существует стандартный набор изображений предложенный Mikolajczyk и др. (включенный в дистрибуцию opencv opencv_extra)
В данном наборе 8 сетов изображений, каждый сет состоит из 6 картинок.
Первая картинка референсная. Остальные пять искаженные, с нарастающей величиной искажений. Каждый сет — для своего типа искажений (вращение, сдвиг, масштаб, выдержка, параллакс, размазывание, де-фокусировка, артефакты сжатия) Вот результаты для различных алгоритмов (SIFT, SURF, AKAZE, BRISK, ORB и разработанного BOEV (Bigraph Oriented Edge Voting)), вертикальная шкала — проценты (больше лучше) и горизонтальная номер картинки в сете (больше- сложнее). Справа от названия алгоритма — время исполнения сета (detection + decription + matching).
Set bark (scale+rotation) precision:
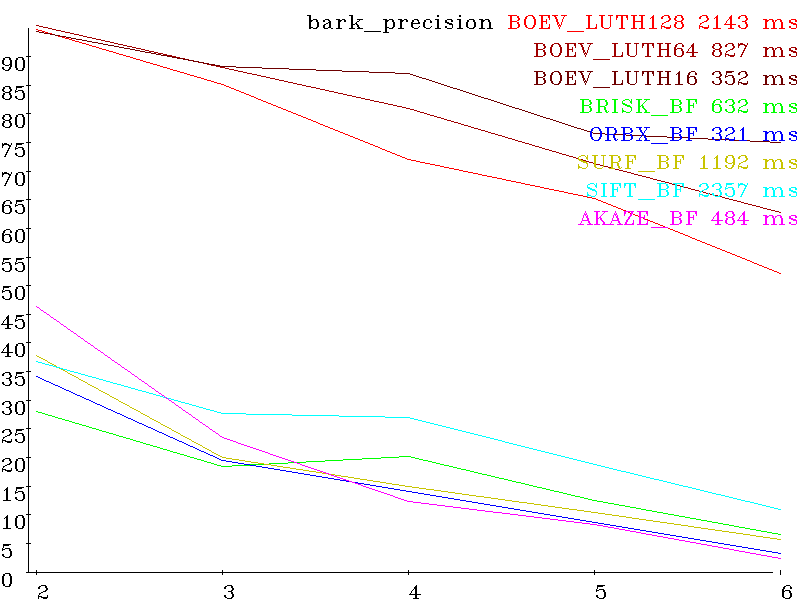
recall:
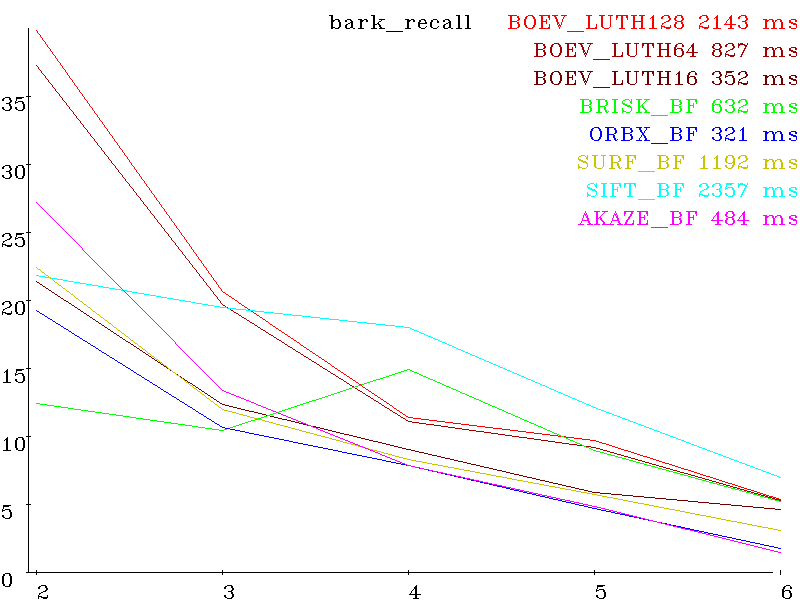
Set bikes (shift + smooth) precision:
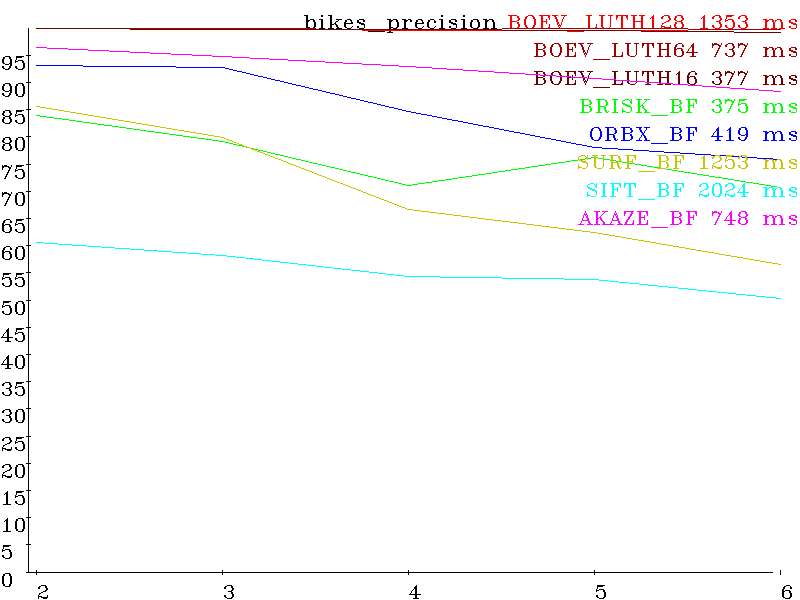
recall:
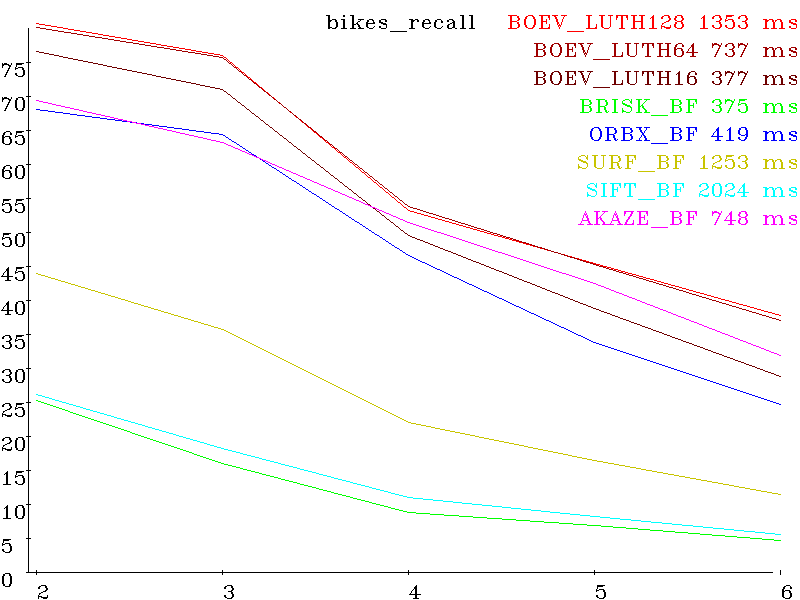
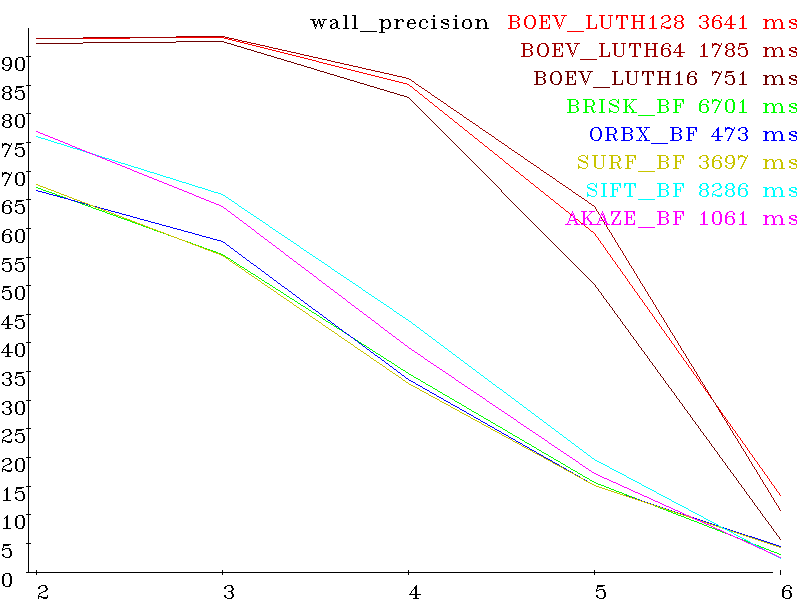
Set wall (perspective distortion) precision:
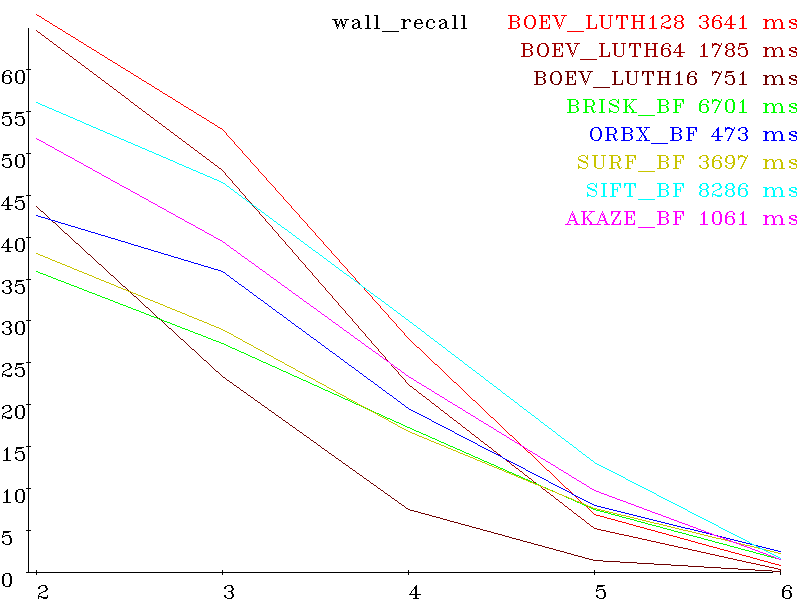
wall recall:
Видимые результаты регистрации на примере wall (красные — false positive, зеленые true positive)

Остальные картинки и исходный код в поддиректории test.
Данный алгоритм показал себя в тестах очень достойно и будет использован в топик проекте.
Дело было вечером…

Существующие системы SLAM не устраивают, или по цене, или по качеству/скорости. Поскольку наработок деталей для Visual SLAM у меня много, решил шаг за шагом писать и выкладывать алгоритмы и код в открытый доступ, с обоснованием причин выбора тех или иных алгоритмов.
В целом план следующий (всё на C++, кроме последнего):
- Захват видео с камеры (в основном
скопипастеннаписан) - Выделение особых точек на каждом 1/1-1/8 кадре изображения (написан)
- Регистрация особых точек (написан)
- Трассировка особых точек (пишется, несложно)
- 3D Реконструкция облака точек и координат камеры в нем (пишется, не очень сложно)
- Драйверы моторов, компаса и тд(в основном
скопипастеннаписан) - Написание хотя бы примитивной логики верхнего уровня, для отладки предыдущего кода (куда и зачем двигаться, на питоне, пока отложено)
Выделение особых точек и их регистрация это критический шаг и по производительности и по аккуратности.Существующие (известные мне) алгоритмы не подходят (для данной платформы), или по скорости, или по аккуратности (precision).
У алгоритмов связывания (matching) точек есть 3 характеристики:
- recall (какой процент точек связан верно из всех детектированных)
- precision (какой процент точек связан верно из всех связанных)
- скорость (время детекции и связывания)
Поскольку связанные точки используются в дальнейшем для нахождения матрицы трансформации при помощи RANSAC метода сложность которого ~O((1/precision)^N) где N — минимальное число пар связанных точек необходимое для вычисления данной матрицы. Если вы ищите плоскость (homography matrix) в 3D (спроецированную в 2D), то N=4, если жесткую трансформацию 3D точек (fundamental matrix), то N=5-8. То есть если, например, precision = 0.1(10%), то для поиска homography вам потребуется десятки тысяч недешевых проб, а для fundamental миллионы. Поэтому был разработан и протестирован алгоритм с высоким precision.
Для проверок алгоритмов детектирования и связывания существует стандартный набор изображений предложенный Mikolajczyk и др. (включенный в дистрибуцию opencv opencv_extra)
В данном наборе 8 сетов изображений, каждый сет состоит из 6 картинок.
Первая картинка референсная. Остальные пять искаженные, с нарастающей величиной искажений. Каждый сет — для своего типа искажений (вращение, сдвиг, масштаб, выдержка, параллакс, размазывание, де-фокусировка, артефакты сжатия) Вот результаты для различных алгоритмов (SIFT, SURF, AKAZE, BRISK, ORB и разработанного BOEV (Bigraph Oriented Edge Voting)), вертикальная шкала — проценты (больше лучше) и горизонтальная номер картинки в сете (больше- сложнее). Справа от названия алгоритма — время исполнения сета (detection + decription + matching).
Set bark (scale+rotation) precision:

recall:

Set bikes (shift + smooth) precision:

recall:

Set wall (perspective distortion) precision:

wall recall:

Видимые результаты регистрации на примере wall (красные — false positive, зеленые true positive)

Остальные картинки и исходный код в поддиректории test.
Заключение
Данный алгоритм показал себя в тестах очень достойно и будет использован в топик проекте.