За последние 10 лет количество товаров-подделок в мире увеличилось в 2 раза. Это данные отчета министерства внутренней безопасности США. Большая часть контрафакта приходится на Китай (56 %), Гонконг (36%) и Сингапур (2%).
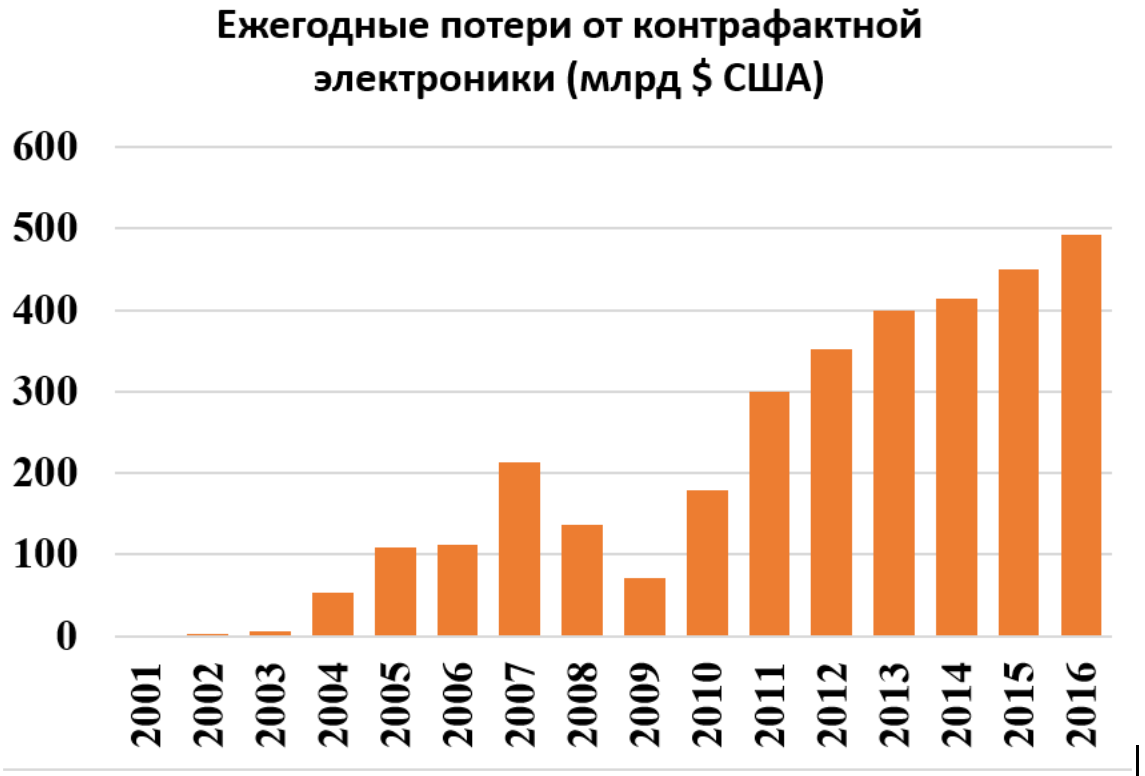
Производители оригинальных товаров несут серьезные убытки, часть из которых приходится на рынок электроники. Многие современные товары содержат в себе электронные компоненты: одежда, обувь, часы, ювелирные изделия, автомобили. В прошлом году прямые потери от незаконного копирования потребительской электроники и электронных компонентов в составе других товаров достигли порядка 0,5 трлн долл. США.
Эту проблему помогают решить различные методы защиты цифровой электроники от нелегального копирования, модификации и обратного проектирования: аппаратное шифрование (AES, RSA и др.), хеширование (например, SHA-256, MD-5), внедрение цифровых водяных знаков и отпечатков пальцев в проектное описание, лексическая и функциональная обфускация, формальная верификация и другие.
В этой статье мы расскажем об одном из самых экономичных методов защиты с точки зрения аппаратных затрат — физически неклонируемых функциях.
Недостатком большинства перечисленных выше методов являются значительные аппаратные затраты и, как следствие, высокое энергопотребление. С возникновением концепции интернета вещей (Internet of Things, IoT) требования к площади, занимаемой цифровым устройством на кристалле интегральной схемы, а также к энергопотреблению становятся более жесткими, поскольку из года в год размер устройств значительно уменьшается.
Одним из способов идентификации и аутентификации цифровых устройств являются физически неклонируемые функции (ФНФ) (Physical Unclonable Functions, PUF), которые значительно более экономичны в реализации чем перечисленные выше методы защиты.
Что такое ФНФ (PUF)? Среди окружающих нас материальных объектов сложно найти два абсолютно одинаковых предмета. Даже в серийном производстве каждый объект получается уникальным за счет погрешностей и случайностей. Эти особенности каждого отдельного объекта можно регистрировать и использовать как уникальный идентификатор, своеобразный «отпечаток пальца».
Наглядный пример — оптическая ФНФ (PUF). Возьмем расплавленное стекло, добавим в него пузырьки воздуха, остудим эту массу и разрежем на одинаковые бруски. Шанс получить два абсолютно одинаковых бруска ничтожно мал, т.к. пузырьки воздуха внутри будут распределены неравномерно. Мы можем зафиксировать эти различия, отправляя на брусок пучок лазерного излучения (запрос), и получая на выходе уникальную интерференционную картину пучков излучения после преломления (ответ). В результате мы получим физически неклонируемую функцию, которая будет определять зависимость ответа от входного запроса. Конечно, эта функция не аналитическая, заранее ее не сможет узнать ни законный обладатель объекта, ни злоумышленник. Можно только протестировать партию изделий и составить таблицу входных и выходных значений, которая и будет служить критерием для определения подлинности объектов.
ФНФ (PUF) для защиты электроники основаны на использовании вариаций технологического процесса (Manufacturing Process Variations) изготовления интегральных схем: например, точных значений пороговых напряжений, задержек распространения сигналов, частоты работы компонентов и т.п. В стандартном процессе проектирования разработчики цифровых устройств стремятся уменьшить влияние вариаций на конечный продукт. В случае ФНФ, напротив, данное неконтролируемое явление используется для извлечения случайности и уникальности цифрового устройства.
Собственно, ФНФ похожи на аппаратные реализации хеш функций, с тем лишь различием, что уникальность выходного значения ФНФ основана на уникальности конкретной интегральной схемы, а не на математическом алгоритме. Входной аргумент ФНФ принято называть запрос (Challenge, CH), а выходное значение — ответом (Response, R). Таким образом, для некоторой интегральной схемы ICk множество запросов {CH0, …, CHN-1} будет уникально отображено в множество ответов {R0, …, RN-1} с помощью ФНФ:
Множество пар запрос-ответ (Challenge-Response Pairs, CRP) {(CH0, R0), …, (CHN-1, RN-1)} уникально характеризует интегральную схему ICk и не может быть скопировано даже при условии использования абсолютно идентичного проектного описания (см. схему ниже).
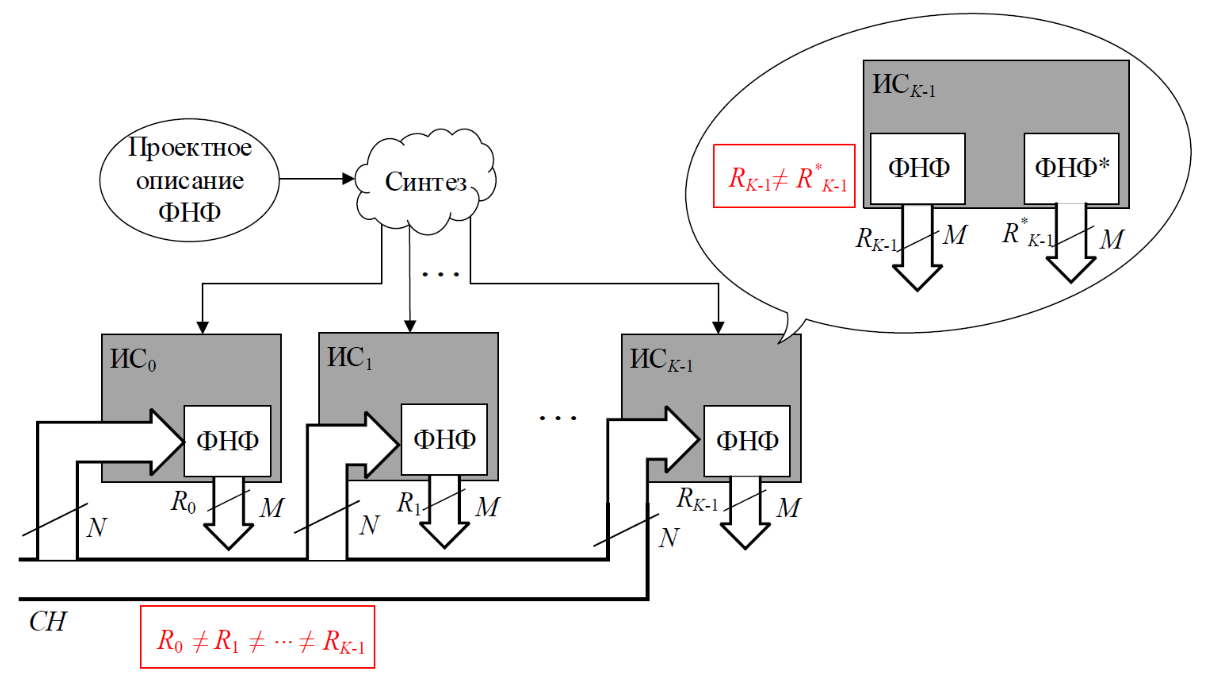
Межкристальная и внутрикристальная уникальность интегральных схем (ИС)
Как показано на схеме, при реализации идентичного проектного описания ФНФ на различных ИС ответы Ri на одинаковый запрос CHi будут уникальны (значительно отличаться друг от друга) для каждой копии. Данное явление называется межкристальной уникальностью, т.е. способностью отличить ИС друг от друга, используя ФНФ. В случае использования идентичных реализаций ФНФ на одном кристалле для идентификации, например, различных компонентов интеллектуальной собственности (Intellectual Property, IP), наблюдается явление внутрикристальной уникальности. Поскольку реализации ФНФ внутри кристалла различны как минимум по взаимному расположению, внитрикристальная уникальность, как правило, более выражена, чем межкристальная.
В настоящее время существует множество реализаций ФНФ на основе:
Как показано выше, существует большое разнообразие типов ФНФ, которые могут быть реализованы как на цифровых устройствах, так и с помощью других технологий (оптические, магнитные, бумажные и т.п.).
Первой коммерческой реализацией ФНФ в 2008 были радиочастотные идентификаторы, изготовленные компанией Verayo. Также в настоящее время многие производители FPGA — например, Xilinx и Altera (Intel) — используют ФНФ в качестве встроенного неклонируемого идентификатора ПЛИС. Поскольку ФНФ используются в качестве криптографических примитивов (генераторов случайных чисел, уникальных идентификаторов, аппаратных хеш функций), многие производители не раскрывают факт использования ФНФ, чтобы хранить в тайне детали реализации их протоколов безопасности от злоумышленников.
Приведем пример реализации ФНФ на основе памяти с использованием ПЛИС Xilinx Spartan 3E, входящей в состав платы быстрого прототипирования Digilent Nexys-2. Эмуляция элемента памяти была реализована в качестве бистабильного элемента, а включение\выключение питания было смоделировано с помощью перепрограммирования ПЛИС одним и тем же конфигурационном файлом.
На рисунке ниже показаны идентификаторы двух идентичных ПЛИС, полученные в результате их программирования одинаковым bit-файлом. Черным цветом обозначены «элементы памяти», которые сохраняют значение 0 в результате 100 перепрограммирований, белым — сохраняющие значение 1. Оттенками серого обозначены те из них, которые меняют значение от запуска к запуску. Соответственно, чем больше в цвете «элемента» черного, тем больше значений 0 было выработано в результате перепрограммирования.

64-разрядные идентификаторы двух идентичных ПЛИС
Как видно из рисунка, «карты памяти» отличаются значительно: Хэммингово расстояние для 64-разрядных идентификаторов составляет порядка 20. Соответственно, вероятность того, что идентификатор будет одинаковым на различных ПЛИС достаточно мала (менее 0,01). Приведенные выше «карты памяти» могут быть использованы двумя способами: для идентификации ПЛИС и в качестве источника случайности в силу наличия непостоянных элементов.
Для надежной идентификации потребуется использование кодов коррекции ошибок (Error Correction Codes, ECC) для стабилизации наблюдаемых «карт памяти». В данной работе был использован метод мажоритарного выбора. Для реализации генератора случайных чисел, напротив, требуется «размножение» случайности тех «элементов памяти», значения которых нестабильны. С этой целью был использован сигнатурный анализ в качестве схемы сжатия данных с потерями. Также могут быть использованы стандартные алгоритмы хеширования (например, SHA-256), если ограничения по аппаратурным затратам не столь жесткие.
Несмотря на относительную новизну данной концепции, в 2017 году термин ФНФ отмечает 15-летний юбилей. За это время научное сообщество уже успело изучить как проблемы, так и возможные приложения ФНФ. Одной из основных проблем, которая показана на примере ФНФ на основе памяти, является нестабильность некоторых из значений, что, в свою очередь, вынуждает разработчика прибегать к кодам коррекции ошибок и более надежным архитектурам ФНФ. С другой стороны, наличие очень высокой стабильности подвергает ФНФ риску криптографической атаки с помощью методов машинного обучения, т.е. построения достаточно точной — более 95% — математической модели ФНФ, что изначально (до 2010 года) считалось невозможным в научном сообществе. Тем не менее, использование ФНФ в современных коммерческих приложениях в качестве криптографического примитива доказывает перспективность исследований в области поиска новых архитектур ФНФ, а также усовершенствования характеристик существующих реализаций.
[!?] Вопросы и комментарии приветствуются. На них будет отвечать автор статьи Сергей Заливако (Siarhei Zalivaka), магистр технических наук, аспирант Наньянгского Технологического Университета (Nanyang Technological University), Сингапур. Сергей специализируется на исследовании стабильности физически неклонируемых функций, их уязвимости к моделированию с помощью методов машинного обучения, а также методах активной идентификации интегральных схем (Integrated Circuit Active Metering).
Производители оригинальных товаров несут серьезные убытки, часть из которых приходится на рынок электроники. Многие современные товары содержат в себе электронные компоненты: одежда, обувь, часы, ювелирные изделия, автомобили. В прошлом году прямые потери от незаконного копирования потребительской электроники и электронных компонентов в составе других товаров достигли порядка 0,5 трлн долл. США.

Эту проблему помогают решить различные методы защиты цифровой электроники от нелегального копирования, модификации и обратного проектирования: аппаратное шифрование (AES, RSA и др.), хеширование (например, SHA-256, MD-5), внедрение цифровых водяных знаков и отпечатков пальцев в проектное описание, лексическая и функциональная обфускация, формальная верификация и другие.
В этой статье мы расскажем об одном из самых экономичных методов защиты с точки зрения аппаратных затрат — физически неклонируемых функциях.
Недостатком большинства перечисленных выше методов являются значительные аппаратные затраты и, как следствие, высокое энергопотребление. С возникновением концепции интернета вещей (Internet of Things, IoT) требования к площади, занимаемой цифровым устройством на кристалле интегральной схемы, а также к энергопотреблению становятся более жесткими, поскольку из года в год размер устройств значительно уменьшается.
Физически неклонируемые функции
Одним из способов идентификации и аутентификации цифровых устройств являются физически неклонируемые функции (ФНФ) (Physical Unclonable Functions, PUF), которые значительно более экономичны в реализации чем перечисленные выше методы защиты.
Что такое ФНФ (PUF)? Среди окружающих нас материальных объектов сложно найти два абсолютно одинаковых предмета. Даже в серийном производстве каждый объект получается уникальным за счет погрешностей и случайностей. Эти особенности каждого отдельного объекта можно регистрировать и использовать как уникальный идентификатор, своеобразный «отпечаток пальца».
Наглядный пример — оптическая ФНФ (PUF). Возьмем расплавленное стекло, добавим в него пузырьки воздуха, остудим эту массу и разрежем на одинаковые бруски. Шанс получить два абсолютно одинаковых бруска ничтожно мал, т.к. пузырьки воздуха внутри будут распределены неравномерно. Мы можем зафиксировать эти различия, отправляя на брусок пучок лазерного излучения (запрос), и получая на выходе уникальную интерференционную картину пучков излучения после преломления (ответ). В результате мы получим физически неклонируемую функцию, которая будет определять зависимость ответа от входного запроса. Конечно, эта функция не аналитическая, заранее ее не сможет узнать ни законный обладатель объекта, ни злоумышленник. Можно только протестировать партию изделий и составить таблицу входных и выходных значений, которая и будет служить критерием для определения подлинности объектов.
ФНФ (PUF) для защиты электроники основаны на использовании вариаций технологического процесса (Manufacturing Process Variations) изготовления интегральных схем: например, точных значений пороговых напряжений, задержек распространения сигналов, частоты работы компонентов и т.п. В стандартном процессе проектирования разработчики цифровых устройств стремятся уменьшить влияние вариаций на конечный продукт. В случае ФНФ, напротив, данное неконтролируемое явление используется для извлечения случайности и уникальности цифрового устройства.
Собственно, ФНФ похожи на аппаратные реализации хеш функций, с тем лишь различием, что уникальность выходного значения ФНФ основана на уникальности конкретной интегральной схемы, а не на математическом алгоритме. Входной аргумент ФНФ принято называть запрос (Challenge, CH), а выходное значение — ответом (Response, R). Таким образом, для некоторой интегральной схемы ICk множество запросов {CH0, …, CHN-1} будет уникально отображено в множество ответов {R0, …, RN-1} с помощью ФНФ:
Множество пар запрос-ответ (Challenge-Response Pairs, CRP) {(CH0, R0), …, (CHN-1, RN-1)} уникально характеризует интегральную схему ICk и не может быть скопировано даже при условии использования абсолютно идентичного проектного описания (см. схему ниже).

Межкристальная и внутрикристальная уникальность интегральных схем (ИС)
Как показано на схеме, при реализации идентичного проектного описания ФНФ на различных ИС ответы Ri на одинаковый запрос CHi будут уникальны (значительно отличаться друг от друга) для каждой копии. Данное явление называется межкристальной уникальностью, т.е. способностью отличить ИС друг от друга, используя ФНФ. В случае использования идентичных реализаций ФНФ на одном кристалле для идентификации, например, различных компонентов интеллектуальной собственности (Intellectual Property, IP), наблюдается явление внутрикристальной уникальности. Поскольку реализации ФНФ внутри кристалла различны как минимум по взаимному расположению, внитрикристальная уникальность, как правило, более выражена, чем межкристальная.
Существующие реализации ФНФ и их применение
В настоящее время существует множество реализаций ФНФ на основе:
- Задержек распространения сигналов. С помощью двоичного значения запроса задается конфигурация симметричных путей, по которым распространяются несколько копий одного сигнала. Ответом ФНФ является результат сравнения задержек времени распространения сигналов.
- Частоты работы компонентов. Основа данной ФНФ — сравнение пар идентичных компонентов, частота которых является уникальной. Запросами являются всевозможные пары индексов различных компонентов, а ответами — результат сравнения частоты их работы.
- Состояние памяти. В результате включения питания и/или сброса состояния статических запоминающих устройств (SRAM) значение, изначально хранимое в каждом из элементов памяти (0 или 1), является уникальным и случайным. Запросом в данной ФНФ является включение/выключение питания, а ответом — наблюдаемое состояние каждого из элементов памяти, которое уникально характеризует интегральную схему, на которой ФНФ реализована.
- Изображения на светочувствительной матрице. Каждое изображение, создаваемое с помощью светочувствительной матрицы (Image Sensor) обладает постоянной составляющей шума, который характеризует уникальность реализованной матрицы. Принцип работы данной ФНФ схож с ФНФ на основе сравнения частот с тем лишь отличием, что сравнение осуществляется по значениям порогового напряжения каждого из элементов матрицы.
- Порогового напряжения транзистора. Данный тип ФНФ может быть реализован только аналоговым, поскольку в таком случае разработчик имеет доступ к значениям пороговых напряжений. Основой для данной ФНФ подобно ФНФ на основе частот является сравнение характеристик нескольких транзисторов, используемых в интегральной схеме.
- Токового зеркала. ФНФ данного класса основана на реализации массива токовых зеркал, значения напряжений в узлах которого уникально характеризуют интегральную схему. Запросом в данном случае являются номера столбцов и строк элементов, значения напряжений в которых необходимо сравнить. Ответом, соответственно, является результат сравнения разности напряжений в паре узлов с пороговым значением.
- Силы давления пользователя на экран смартфона. В данной реализации ФНФ запросом является пользовательское действие, которое заключается в проведении пальцем по определенному рисунку (подобно графическому ключу в смартфонах). На основе значений силы давления пользователя на экран смартфона вычисляется уникальное значение ответа, которое характеризует пользователя и смартфон и, таким образом, может быть использовано для аутентификации.
- Структуры бумаги. Данная реализация ФНФ основана на уникальности структуры бумаги, обусловленной вариациями, вносимыми в нее в процессе производства. Соответственно, определенный бумажный носитель может быть использован в качестве источника уникальных криптографических ключей.
Как показано выше, существует большое разнообразие типов ФНФ, которые могут быть реализованы как на цифровых устройствах, так и с помощью других технологий (оптические, магнитные, бумажные и т.п.).
Первой коммерческой реализацией ФНФ в 2008 были радиочастотные идентификаторы, изготовленные компанией Verayo. Также в настоящее время многие производители FPGA — например, Xilinx и Altera (Intel) — используют ФНФ в качестве встроенного неклонируемого идентификатора ПЛИС. Поскольку ФНФ используются в качестве криптографических примитивов (генераторов случайных чисел, уникальных идентификаторов, аппаратных хеш функций), многие производители не раскрывают факт использования ФНФ, чтобы хранить в тайне детали реализации их протоколов безопасности от злоумышленников.
Пример ФНФ на основе памяти (SRAM)
Приведем пример реализации ФНФ на основе памяти с использованием ПЛИС Xilinx Spartan 3E, входящей в состав платы быстрого прототипирования Digilent Nexys-2. Эмуляция элемента памяти была реализована в качестве бистабильного элемента, а включение\выключение питания было смоделировано с помощью перепрограммирования ПЛИС одним и тем же конфигурационном файлом.
На рисунке ниже показаны идентификаторы двух идентичных ПЛИС, полученные в результате их программирования одинаковым bit-файлом. Черным цветом обозначены «элементы памяти», которые сохраняют значение 0 в результате 100 перепрограммирований, белым — сохраняющие значение 1. Оттенками серого обозначены те из них, которые меняют значение от запуска к запуску. Соответственно, чем больше в цвете «элемента» черного, тем больше значений 0 было выработано в результате перепрограммирования.

64-разрядные идентификаторы двух идентичных ПЛИС
Как видно из рисунка, «карты памяти» отличаются значительно: Хэммингово расстояние для 64-разрядных идентификаторов составляет порядка 20. Соответственно, вероятность того, что идентификатор будет одинаковым на различных ПЛИС достаточно мала (менее 0,01). Приведенные выше «карты памяти» могут быть использованы двумя способами: для идентификации ПЛИС и в качестве источника случайности в силу наличия непостоянных элементов.
Для надежной идентификации потребуется использование кодов коррекции ошибок (Error Correction Codes, ECC) для стабилизации наблюдаемых «карт памяти». В данной работе был использован метод мажоритарного выбора. Для реализации генератора случайных чисел, напротив, требуется «размножение» случайности тех «элементов памяти», значения которых нестабильны. С этой целью был использован сигнатурный анализ в качестве схемы сжатия данных с потерями. Также могут быть использованы стандартные алгоритмы хеширования (например, SHA-256), если ограничения по аппаратурным затратам не столь жесткие.
Существующие проблемы и перспективы ФНФ
Несмотря на относительную новизну данной концепции, в 2017 году термин ФНФ отмечает 15-летний юбилей. За это время научное сообщество уже успело изучить как проблемы, так и возможные приложения ФНФ. Одной из основных проблем, которая показана на примере ФНФ на основе памяти, является нестабильность некоторых из значений, что, в свою очередь, вынуждает разработчика прибегать к кодам коррекции ошибок и более надежным архитектурам ФНФ. С другой стороны, наличие очень высокой стабильности подвергает ФНФ риску криптографической атаки с помощью методов машинного обучения, т.е. построения достаточно точной — более 95% — математической модели ФНФ, что изначально (до 2010 года) считалось невозможным в научном сообществе. Тем не менее, использование ФНФ в современных коммерческих приложениях в качестве криптографического примитива доказывает перспективность исследований в области поиска новых архитектур ФНФ, а также усовершенствования характеристик существующих реализаций.
[!?] Вопросы и комментарии приветствуются. На них будет отвечать автор статьи Сергей Заливако (Siarhei Zalivaka), магистр технических наук, аспирант Наньянгского Технологического Университета (Nanyang Technological University), Сингапур. Сергей специализируется на исследовании стабильности физически неклонируемых функций, их уязвимости к моделированию с помощью методов машинного обучения, а также методах активной идентификации интегральных схем (Integrated Circuit Active Metering).