Просто о графах. Попытка популяризации

«Всякие звания (дворянина, купца, мещанина, крестьянина и пр., титулы — княжеские, графские и пр.) и наименование гражданских чинов (тайные, статские и проч. советники) уничтожаются...»

Об уничтожении сословий и гражданских чинов
Декрет ВЦИК и СОВНАРКОМа от 10.11.1917 года, ст. 2

---

Как-то же я обходился без этого раньше...

Есть ли польза рядовому программисту или, скажем, обывателю от теории графов, или вещь эта сугубо сакральная, из надменных математических абстракций?

Вероятно, специфика “случайно распределенных графов” окажется маловостребованной в нашей с вами повседневности, но некоторое представление о теории графов может оказаться полезным в самых разнообразных ситуациях даже человеку не особенно к математике расположенному, – что же касается людей, занятых в такой области, как программирование, то изощренная изобретательность, как правило, сопутствует ежедневно выпадающим на их долю задачам, оттого представители этой профессии, в поисках новых идей и инструментов, случается, азартно загружают свой ум вещами, казалось бы не пригодными для полезного использования, однако, заказав пиццу за 10 тысяч биткоинов, они дарят хорошее настроение другим хорошим людям на многие годы, и таки оправдывают свою пассионарность.

Ну мы, допустим, себя причисляем к людям вполне серьезным и намерены вполне серьезно обратить себе на пользу малую толику знаний, которую мы трудно накапливаем и, с годами всё с более возрастающим трудом, удерживаем в своей голове. И роскошь небрежного забвения единожды усвоеной нами информации решительно отвергаем.

Граф может быть прекрасным средством визуализации посетившей вас идеи. Мы каждый день решаем какие-либо задачи, которые могут быть адекватно записаны языком графов, но часто не испытываем потребности в манипулировании зрительными образами. Иногда же именно зрительный образ оказывает то необходимое действие на нашу мыслительную концентрацию, которое приводит нас к светлой идее. – Часто оказывается полезным взглянуть на вещи с разных ракурсов.

Граф может оказаться выразителем сущности некоторой идеи и сократить вашу дорогу к конечной цели (если вы сейчас подумали о грустном, то я не имел это ввиду).
Часто бывает, что мы пользуемся не осознано, интуитивно, некоторыми приемами решения возникающих перед нами задач, которые – суть пользовательские шаблоны, подсказанные предыдущим опытом, а между тем, эти приемы, отлитые в идею, возведенные в парадигму, обращенные в концепцию могут стать мощнейшим инструментом, указывающим нам как направление, так и способ решения целого класса объединенных общим признаком проблем.

Теория графов к настоящему времени содержит достаточно много эффективных инструментов для решения столь же широкого круга проблем. Однако, средства и идеи, сегодня относящиеся к области дискретной математики, именуемой теорией графов, пребывают по сей момент в некотором эклектичном единстве как бы не без насильственного понуждения. Круг вопросов, решаемых теорией графов, и разнообразие привлекаемых для этого моделей и механизмов их решения столь обширны, что попытки популяризовать теорию графов в целом должны опираться на немалую дерзость. Академическое и глубокое изложение специфических нюансов теории графов не будет целью настоящей статьи. У нас есть намерение говорить лишь о том, чему мы нашли полезное (или относительно полезное) и нескучное применение.

И между прочим, «откуда есть пошло» теория графов?

Отдадим дань уважения великим именам и кратко обратимся к историческим ретроспекциям.

… Это решение по своему характеру; по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике.

Из письма Леонарда Эйлера к своему другу Карлу Готлибу Элеру, 03 [14] апреля 1736 г.^[1]



Рис. 1. Кёнигсберг на гравюре 17 века.

Считается, что теория графов начала оформляться как самостоятельная математическая дисциплина после показательного решения Эйлером "задачи о семи мостах",– задачи чисто логистической,– применение теории графов к решению "задачи с четырьмя цветными кубиками", на мой взгляд, требовало значительно большей изобретательности и большой искушенности в предмете, достигаемыми лишь постоянными упражнениями в практическом применении теории графов, хотя, к моменту решения последней из упомянутых задач от цитируемой переписки минуло более двух веков, и предмет новой дисциплины, лишь туманно виденной Эйлером, успел приобрести очертания вполне конкретные и накопить некоторый опыт практического применения усилиями выдающихся ученых, развивавших идеи Эйлера.

[Рис. 1 может дать некоторое представление о «задаче», упоминаемой в процитированной фразе.] Частью городской коммуникации и архитектурного ансамбля города Кёнигсберга в 1736 году являлись 7 мостов (эти старые мосты не сохранились) через реку Прегель. Трудно сказать, насколько широко была распространена загадка о том, можно ли пройти по всем семи мостам, не пройдя дважды ни по одному из них, и серьезно ли городские службы думали над утверждением такового маршрута для гостей города и горожан, но эта загадка сумела привлечь внимание Леонарда Эйлера, – правда, оставалась довольно длительное время единственным известным примером применения метода, предложенного великим математиком. Более ста лет работа Эйлера не вызывала особого интереса у ученого сообщества. Термин «граф» ввёл венгерский математик Дениш Кёниг только в 1936 году.

Некогда мне была предложена задача об острове, расположенном в городе Кёнигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно.

Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения не достаточны ни геометрия, ни алгебра, ни комбинаторное искусство.

Из письма Леонарда Эйлера к Джиованни Джакобо Маринони, 13 [24] марта 1736 г.^[2]

(Судя по письмам Леонарда Эйлера, великий ученый не без удовольствия решал и другие головоломные задачи..)

Задача о семи мостах

Решение её изложено подробно в письмах к Элеру и Маринони.

Наконец, ты, славнейший муж, выражаешь желание ознакомиться с моим способом построения мостов; охотно представляю этот способ на твой суд. Ибо, когда ты попросил у меня решения этой проблемы, приспособленной к частному случаю Кёнигсберга, ты, вероятно, считал, что я предложил такого рода построение мостов, но я не сделал это, а только доказал, что такое построение вообще не может иметь места, и это следует принять вместо решения. Способ же мой является универсальным, так как с его помощью в любом предложенном мне случае этого рода я тотчас могу решить, следует ли строить переход с помощью отдельных мостов или нет, и в первом случае [могу установить], каким образом этот переход следует осуществить. Далее я изложу мой способ, а также опишу путь, которым я к нему пришел.

Карлу Готлибу Элеру, 03 [14] апреля 1736

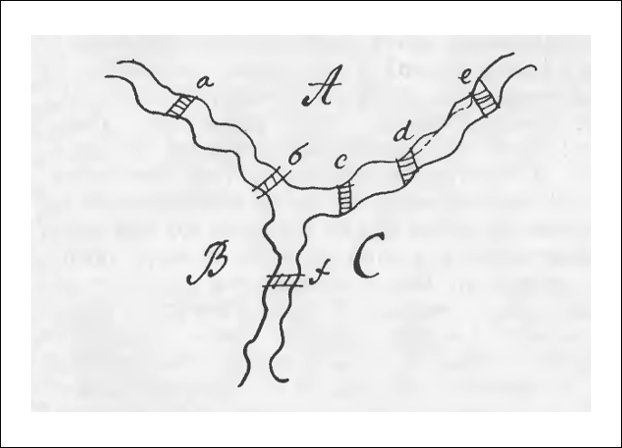
Я рассмотрел произвольно взятую фигуру разветвления реки, а также мосты а, b, с, d, e, f, как это указано на рисунке, и установил, что возможен переход, который я представляю следующим образом. Области, отделенные друг от друга водой, я называю буквами А, В, С, и когда предполагается переход через мосты из одной области в другую, [а именно] переход из А в В через мост или а или b, — наиболее удобно назвать [буквами] АВ, из которых первая буква А будет обозначать область, из которой переходят. Итак, АВСАСАВ будет определять переход, совершаемый через все мосты по одному разу; число этих букв должно быть на единицу больше, чем число мостов; это должно иметь место при любом возможном переходе описанным способом, в чем каждому легче убедиться самому, чем доказывать. Теперь я рассматриваю, сколько раз в ряде букв А, В, С, А, С, А, В должны встретиться буквы ABC, о чем нужно судить по числу мостов, ведущих в каждую из областей. Так, к области А ведут пять мостов: а, b, с, d, e, и сколько раз буква А встречается в середине того ряда, столько раз встречаются два из этих мостов, ибо с одной стороны нужно перейти в область А, с другой стороны — выйти оттуда. Если А встречается или в начале, или в конце того ряда, тогда единственный переход моста соответствует А. Отсюда следует, что, если число мостов, ведущих в область А, будет нечетным, тогда переход через все мосты не может совершиться иначе, чем таким образом, чтобы он или начинался в области А, или заканчивался в области А. А если число мостов, ведущих к А, будет четным, тогда переход может быть совершен и без этого условия, чтобы начинаться или заканчиваться в А, но если он начинается в А, то должен будет там же и закончиться. Отсюда вытекает, что в ряде АВСАСАВ любая буква, за исключением первой и последней, обозначает переход, ведущий через два моста в область, обозначенную этой буквой.

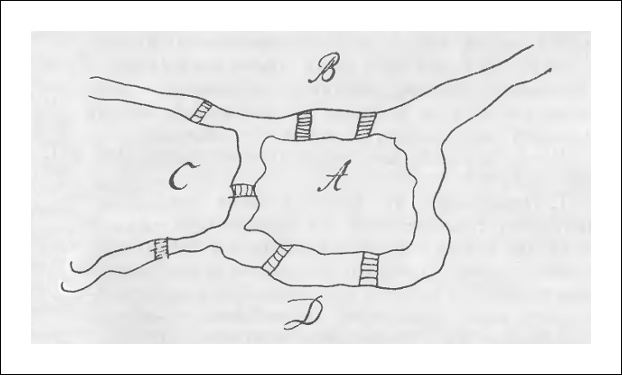
Следовательно, надо держаться следующего правила: если на каком-либо рисунке число мостов, ведущих в некоторую область, будет нечетным, тогда желаемый переход через все мосты одновременно не может быть осуществлен иначе, как если переход или начинается, или заканчивается в этой области. А если число мостов четное, отсюда не может возникнуть никакого затруднения, так как ни начало, ни конец перехода при этом не фиксируются. Отсюда следует такое общее правило: если будет больше чем две области, к которым ведет нечетное количество мостов, тогда желательный переход вообще не может быть совершен. Ибо представляется совершенно невозможным, чтобы переход и начинался, и заканчивался в какой-нибудь одной из этих областей. А если будут только две области такого рода (так как не могут быть даны одна область этого рода или нечетное число областей), тогда может быть совершен переход через все мосты, но с таким условием, чтобы начало перехода было в одной, а конец в другой из этих областей. Когда в предложенной фигуре А и В есть области, к которым ведет нечетное число мостов, а число мостов, ведущих к С, является четным, то я считаю, что переход или построение мостов может иметь место, если переход начинается или из А, или из В, а если же кто-нибудь пожелает начать переход из С, то он никогда не сможет достигнуть цели. В расположении кенигсбергских мостов я имею четыре области А, В, С, D, взаимно отделенные друг от друга водой, к каждой из которых ведет нечетное число мостов.

Таким образом, поскольку есть больше чем две области, к которым ведет нечетное число мостов, я утверждаю, что я доказал полную невозможность такого соединения мостов. Итак, с помощью очень легкого правила можно почти мгновенно определить для любой фигуры, допускается ли такого рода построение мостов, при котором переход будет происходить только через все мосты одновременно, или нет? Ибо возможным будет построение, если и не будет никакой области, или будут только две, к которым ведет нечетное число мостов; в таких случаях начало перехода выбирается произвольно, но там же должен быть и конец перехода. В последнем же случае начало перехода должно иметь место в одной из тех областей, а конец — в другой. Построение невозможно, если будет более чем две области, к которым поведет нечетное число мостов.

 

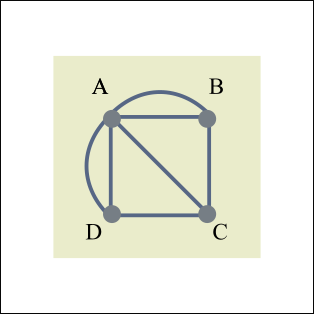
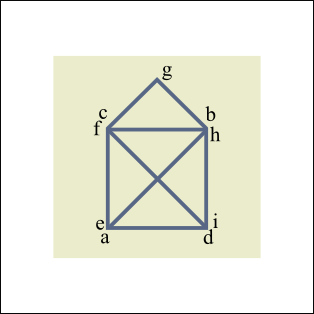
Рис. 2. Граф Кёнигсбергских мостов.
Рис. 3. Головоломка «Конверт».

Следовательно, ты можешь убедиться, славнейший муж, что это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешаются математиками, чем другими [учеными]. Между тем ты, славнейший муж, определяешь место этого вопроса в геометрии положения, и что касается этой новой науки, то, признаюсь, мне неизвестно, какого рода относящиеся сюда задачи желательны были Лейбницу и Вольфу. Итак, я прошу тебя, если ты считаешь, что я способен нечто создать в этой новой науке, чтобы ты соблаговолил мне прислать несколько определенных, относящихся к ней задач, для того, чтобы я мог лучше уяснить себе, что именно представляется желательным. Между тем, поскольку мне известно, что Ты также можешь составить суждение о математических науках на основании одной только задачи, которую следует предложить и решить, начало чему по Твоей просьбе предложил преславный Кюн, я хотел бы, чтобы он представил нам такого рода задачи, которые он считает более трудными, [сделав это] как для прогресса науки, так и для упражнения наших сил.

Едва ли приведенные выше рассуждения Леонарда Эйлера вызвали у вас благоговейный трепет, какой, например, совершенно извинителен для человека, сколько-нибудь приобщенного к математике, восхищенно перебирающего следствия эффектной формулы Эйлера для комплексных чисел.

небольшое отступление

Следствие Формулы, связывающее пространства иррациональных и мнимых чисел:

Поскольку из Формулы Эйлера следует, что , нетрудно видеть, что

Впрочем, впечатлиться можно простым перечислением заслуг этого великого человека перед наукой…

Однако же, уж очень эта трёхсотлетней давности «задача о Кенигсбергских мостах» (Рис. 2) напоминает вам «конвертик», который в начальных классах вы успешно рисовали в «один проход» (Рис. 3), с каждым новым открытым вами способом нарисовать этот «конверт» умножая свое торжество над соревнующимися с вами в этом занятии одноклассниками.

Сколько сегодня найдете маршрутов? Полагаю, что внимательно читавшие выше письма Эйлера не ошибутся в выборе начальных точек для построения своих маршрутов (в первом классе у вас не было такой подсказки?), и предсказать, где их маршруты завершатся, тоже не составит труда. Заодно, достройте восьмой мост в «городе мыслителей» и наполните желанным смыслом пешие прогулки его жителей.

А мостов могло быть и больше...

В задачнике Генри Э.Дьюдени «520 головоломок» (я располагаю изданием 1975 года, Издательство «Мир», Москва^[3]) есть немало задач, которые могут быть решены прямо по инструкциям Эйлера. Взглянем на одну из таких задач, которой в указанном издании присвоен номер 408.

Эйлер вооружил нас надежным приемом, и мы решим задачу Дьюдени №408 запросто. Однако, скажем прямо, когда эта книга у меня завелась, я и представления не имел о рекомендациях Эйлера.

• 408. Двадцать два моста Вы видите здесь схему района с развитой системой ирригационных сооружений, на которой указаны многочисленные каналы и мосты. Человек выходит с одного из участков, обозначенных буквами, чтобы навестить приятеля, живущего на другом участке. Желая при этом совершить моцион, он проходит по каждому мосту один и только один раз.

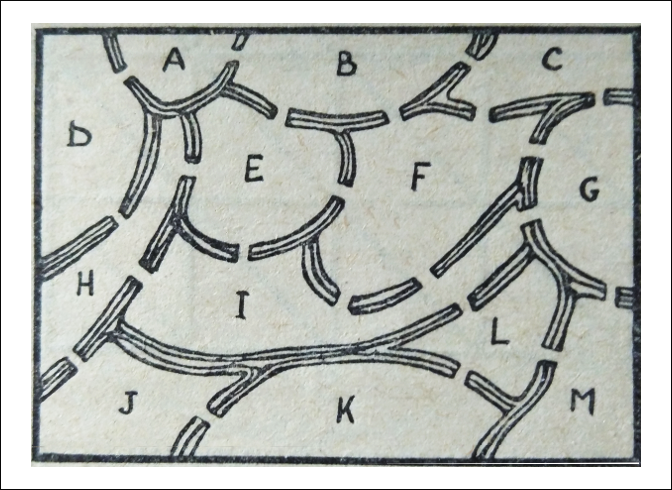
• Головоломка состоит в том, чтобы выяснить, на каких участках расположены дома приятелей. Она покажется вам чрезвычайно простой, если вы подумаете над ней несколько минут. Разумеется, не следует выходить за пределы схемы.

Прямо вот «чрезвычайно простой»?..
…
Что делать, если я хочу в своем маршруте учесть расписание городских достопримечательностей? – Например, часть мостов вдоль моего маршрута следования являются разводными, и всякие раз проходя по ним я досадую, что не могу полюбоваться их механикой в действии, или, напротив – именно эта их особенность подгоняет мой шаг, дабы успеть миновать эти мосты до начала комендантского часа.

Зная путь, указанный нам великим математиком, мы способны, пожалуй, и на некоторые самостоятельные шаги. Как часто бывает, если часть задачи решили за нас, оставшуюся часть решить уже кажется проще. Зная, где мне сделать первый шаг, я, пожалуй, могу написать короткую инструкцию для подсчета или даже диспетчеризации возможных маршрутов.

Подсчет переходов

Если вы решите повторить эти вычисления, не забудьте, что нечетный узел «С», с которого я начинаю движение, имеет степень 3. Этой же программой можно посчитать «конверт» и сравнить результат с маршрутами, найденными «вручную».

package com.ozrio.tracepath;

/**
 *
 * @author nailer
 */
public class TracePath {
    private static final String[] nodes = {"A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M"};

    public static void main(String[] args) {
        final int[][] edges = {{1,3}, {0,2,4,5}, {1,5,6}, {0,7}, {1,5,7,8}, {1,2,4,6,8,8}, {2,5,8,12}, 
                               {3,4,8,9}, {4,5,5,6,7,11}, {7,10}, {9,11}, {8,10,12}, {6,11}};
        int[] pr = new int[23];
        pr[0] = 2;
        System.out.println("" + branch(2, 0, 1, edges, pr)); // _to : 0,1,2
    }
    
    private static int branch(int _from, int _to, int countEdge, int[][] listEdges, int[] pathResult) {
        int[][] le = removeEdgeFromArray(_from, _to, listEdges);
        pathResult[countEdge++] = listEdges[_from][_to];
        if (countEdge == pathResult.length) {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < pathResult.length; i++) sb.append(nodes[pathResult[i]]);
            System.out.println("path : " + sb.toString());
        }
        
        for (int i = 0; i < le[listEdges[_from][_to]].length; i++) {
            int[] pr = new int[pathResult.length]; // 22
            System.arraycopy(pathResult, 0, pr, 0, pathResult.length);
            branch(listEdges[_from][_to], i, countEdge, le, pr);
        }
        return 0; // stop branch if (listEdges[_from].lenght == 0)
    }
    
    private static int[][] removeEdgeFromArray(int node, int indexEdge, int[][] oldListEdges) {
        int[][] shortcutList = new int[13][];
        shortcutList[node] = new int[oldListEdges[node].length - 1];
        shortcutList[oldListEdges[node][indexEdge]] = new int[oldListEdges[oldListEdges[node][indexEdge]].length - 1];
        int q1 = 0, q2 = 0, i, j;
        boolean once1 = true, once2 = true; // in case edge more than one
        for (i = 0; i < shortcutList.length; i++) {
            if (i == node) {
                for (j = 0; j < oldListEdges[node].length; j++) {
                    if (j == indexEdge  && once1) {
                        once1 = false;
                        continue;
                    }
                    shortcutList[node][q1++] = oldListEdges[node][j];
                }
            } else if (i == oldListEdges[node][indexEdge]) {
                for (j = 0; j < oldListEdges[oldListEdges[node][indexEdge]].length; j++) {
                    if(oldListEdges[oldListEdges[node][indexEdge]][j] == node  && once2) {
                        once2 = false;
                        continue;
                    }
                    shortcutList[oldListEdges[node][indexEdge]][q2++] = oldListEdges[oldListEdges[node][indexEdge]][j];
                }
            } else {
                shortcutList[i] = new int[oldListEdges[i].length];
                System.arraycopy(oldListEdges[i], 0, shortcutList[i], 0, oldListEdges[i].length);
            }
        }
        return shortcutList;
    }
}

Итого, маршрутов насчитывается 67344 вариантов. Несколько многовато, но настоящая дружба должна быть способна вынести и такое количество визитов, осталось найти «настоящую» обувь, т.к. это испытание и для неё.

Пути и деревья

Графические схемы, конечно же, не исчерпываются замкнутыми маршрутами, и наш путь ведет нас к деревьям…

С 1978 года в мире, лежащем за пределами ваших компьютеров, то там, то сям, и никогда не здесь, происходят нешумные или даже почти конспиративные встречи незнакомых со мной (я так полагаю) людей, зовущиеся International Puzzle Party. Получить приглашение на это мероприятие можно только от члена этого закрытого клуба. Где и когда произойдет следующая встреча, никогда не известно за пределами клуба. Если верить лаконичному анонсу официального сайта IPP, то опаснее рукопожатий коллекционеров головоломок на самих «пати» ничего не происходит. Однако, постфактум тайного собрания, прочим смертным случается увидеть каталог диковинных головоломок, тщательно проинспектированных искушенным в головоломных задачах комитетом этого элитарного форума. Одна из таких головоломок, представленная на IPP 37, проходившем в августе 2017 года в Париже (вы тоже почувствовали влечение к коллекционированию головоломок?), была предложена участником «форума нешарнирных головоломок» (я несведущ в его международных перемещениях) в качестве разминки для мозгов охочим до такого досуга коллегам.

Мне эта головоломка показалась несколько напоминающей задачу Дьюдени, обремененную, однако, несколькими нюансами.

Разработчиком (создателем, творцом, демиургом) этого образца неординарной мысли, шедевра изощренной человеческой изобретательности отмечен Donghoon Pee – творец, видимо, скромный и незаслуженно малоизвестный здесь на Хабре,– последнюю несправедливость мы сейчас исправим, хотя, конечно, загубим интригу… Мне и самому жалко лишать читателей Хабра возможности самостоятельно поразмыслить над головоломкой 2&1 автора Donghoon Pee – могу лишь посоветовать тем, кто страстно желает решить головоломку самостоятельно, закрыть ладошками рисунки и часть относящегося к головоломке текста ниже.

У Donghoon Pee (Донгун Пи – наиболее вероятное прочтение, но, чтобы не рисковать, буду пользоваться латинским написанием) есть свой канал на youtube.com, страница в фейсбуке, проживает он в городе Сеуле и является профессиональным создателем (язык не поворачивается сказать «дизайнером», хотя сам он именно так зовет свой род занятий) головоломок. И его работы не раз удостаивались внимания клуба IPP. Будем надеяться, доходы этого безусловно достойного человека не понесут ущерба от этой публикации.

• На зеленом поле строго определенного размера надо разместить пять плиток различной формы, каждая из которых состоит из двух цветов. Центральная ячейка в поле является трёхцветной – с любым из цветов этой ячейки контактировать может лишь соответствующий цвет плитки, т.е. если боковая полоска центральной ячейки окрашена в красный цвет, иным цветом, кроме красного, плитка касаться этой боковой поверхности ячейки не должна. Цель головоломки: уложить все пять плиток на игровое поле так, чтобы каждый из трех цветов элементов плиток образовал неразрывное цветовое поле.

Если мы продолжим аналогию с островами и мостами, то, разбив поле на клетки, мы можем полагать эти клетки «островами» между которыми мы перебрасываем «мосты»-плитки. Не сказать, что наши «мосты» послужат кому бы то ни было образцом архитектуры, но, для нашей узкой задачи, такая условность вполне уместна. Ограничив условия «строительства мостов» требованием контакта совпадающих цветов в разных плитках, и введя критерий «неразрывности цвета» (ну и логично, конечно, будет начать «строительство» с центральной ячейки), мы можем запустить рекурсивное построение графа дерева, которое не окажется особо продолжительным, ввиду незначительности «строительного материала». Корнем нашего дерева является центральная ячейка, и в любом узле такого дерева допустимо множественное ветвление.

Небольшая модификация задачи может превратить её в задачу на плотную упаковку и т.п., но в узнаваемых пределах мы можем придерживаться модели, допускаемой теорией графов. Разумеется, с ростом серьезности поставленной задачи может возникнуть необходимость учета алгоритмической сложности и ограниченности рекурсивного механизма.

Задача с четырьмя цветными кубиками

Попробуем придать нашему обозрению видимость чуть большей академичности, для чего еще раз обратимся к «головоломке с четырьмя цветными кубиками».

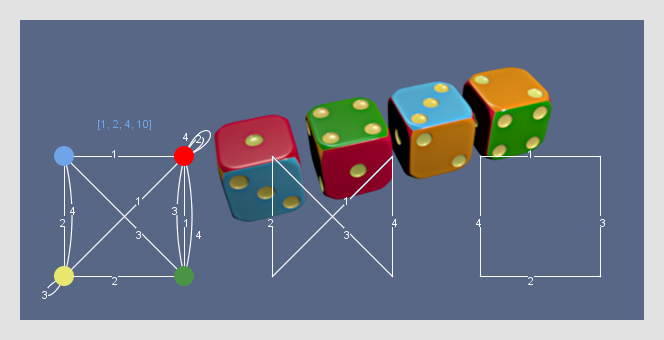
Решая эту головоломку методом обычного перебора, мы прибегаем к методу обещающему нам 41472 иттераций. Изящнейшее же решение в графах потребует перебора комбинаций из четырех кубиков, описанных тремя парами цветов. – Разница ощутимая. Напомню легко алгоритмизируемую процедуру:

граф кубика в этой головоломке – это графическая модель, в 4-х узлах которой расположены 4-е цвета, а каждое ребро указывает/связывает пару противоположных граней: остроумная мысль, пришедшая в голову F. De Carteblanche (Cedric A. B. Smith) заключалась в том, что два набора по четыре цвета в каждом могут быть описаны в виде графа с узлами степени 2, где сами узлы означают цвета, а ребра графа указывают на то, что пара состоит в различных, а не в одном, наборах – соотнеся пару с родительским кубом (путем нумерации ребер), мы получим однозначные указания для размещения в пирамиде этого комплекта граней.

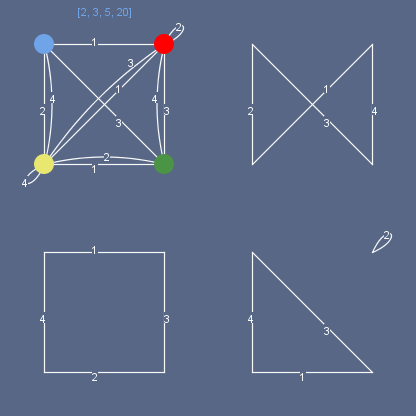Имея инструкции для второго набора – т.е. для второй пары граней пирамиды, мы можем окончательно собрать комбинацию, являющуюся решением головоломки. Таким образом, выделив из мультиграфа (совокупности графов кубиков) два подграфа, указывающих на различные наборы цветов, – а для этого достаточно, чтобы одно и тоже ребро (поскольку именно ребро указывает на связь) не использовалось одновременно в каждом из графов,– мы получим легко читаемое решение головоломки: нам достаточно, например, согласно первой инструкции расположить кубики в соответствии «верх-низ» и привести их в соответствии со второй инструкцией, поворачивая вправо-влево. [Напомню, что «петля» так же является узлом 2-ой степени]. Из всех представленных на рисунке подграфов, только два образуют пару с несовпадающими ребрами. Это так называемое «единственное решение» «правильной» головоломки.


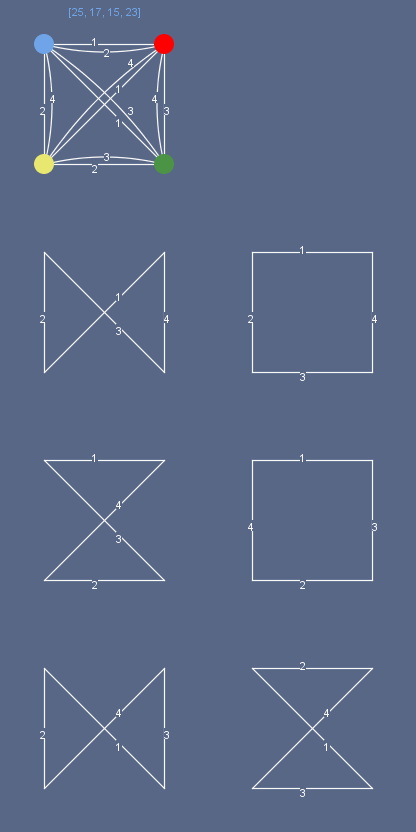Не лишнее, вероятно, подробно рассмотреть пример развертки мультиграфа для красивой сборки, имеющей в 24-х положениях на каждой из своих сторон все 4-е цвета («неправильная» головоломка, на предыдущей публикации предыдущей публикации она представлена на Рис. 6): три подграфа (на левом рисунке, это три крайних левых подграфа) могут складываться в три пары с несовпадающими ребрами – сборка с «тремя решениями» по терминологии, распространенной в англоязычной среде.

Если мне в некотором, условно говоря, «потоке кубических сущностей» понадобится «выловить симметричные сборки», я постараюсь избежать банального перебора. Например, из кубиков, развертки которых приведены на Рис.2 той же публикации можно быстро сложить 16 наборов с «тремя решениями».

Граф указывает нам на внутреннюю связь, на уникальную природу некоторой изучаемой нами вещи. Воспользоваться замеченной особенностью вполне естественно, особенно, если модель обещает нам некоторое преимущество в сравнении с другими путями решения задачи.

 

Обратное моделирование

Можно ли от желаемой графической модели перейти к конкретной реализации чего бы то ни было? – Едва ли существует однозначный ответ, но в большинстве случаев я бы советовал не пытаться осуществить подобные переходы, если только искомая вами модель не ограничивается полностью описываемыми в рамках графического прототипа особенностями. Описывая объект из реального мира, вы пренебрегаете частью его свойств перед одной сущностной особенностью, в угоду выбранной вами модели.

Например, у 1073-х уникальных наборов кубиков по четыре число отвечающих этим наборам уникальных графов существенно меньше: если принимать во внимание в топологии графа лишь сочетание его ребер и узлов, опуская нумерацию ребер, то можно выделить лишь 204 уникальных графов для возможных головоломок из четырех цветных кубиков.

Графы решений,— те два пути обхода узлов, которые необходимо выделить из мультиграфа,– будут подобны, хотя сам исходный мультиграф может делиться различным образом, т.к. нумерация граней все-таки вносит особенности в общую топологию графа. Графическая модель, которую мы используем для нахождения решения головоломки, подобной Instant Insanity, характеризует наборы кубиков только с точки зрения оптимизации поиска решения этой головоломки. Эта модель построена на основе анализа топологической структуры набора кубиков для решения только одной узкой задачи – задачи взаимного расположения кубиков. Отдельный мультиграф, как и граф отдельного кубика, не указывает на уникальность объекта, да и не должен – мы же сами искали нечто общее в явлении, а не в объекте. Портретный образ не предстает из лаконичной характеристики «характер – твердый, нордический».

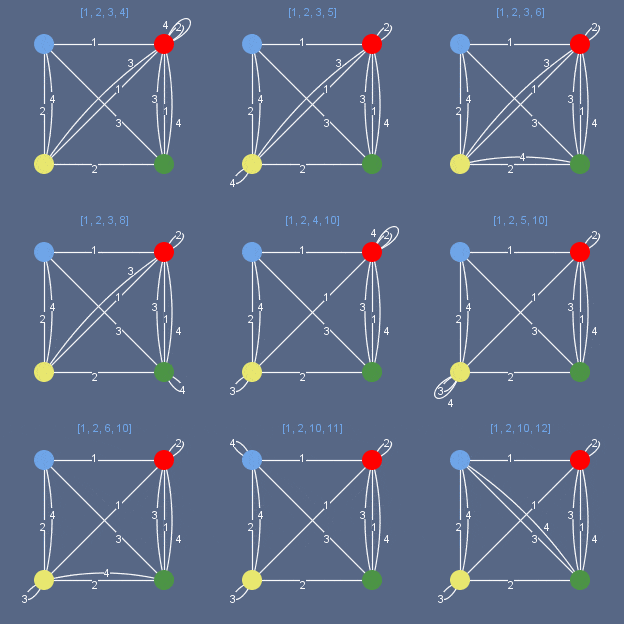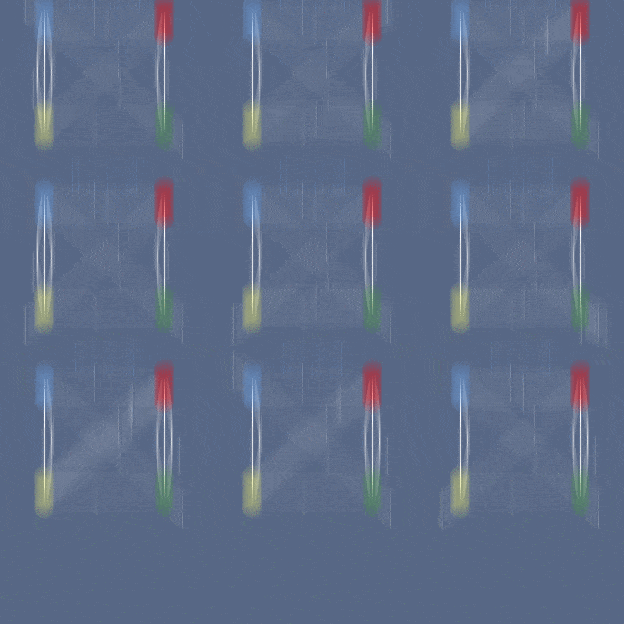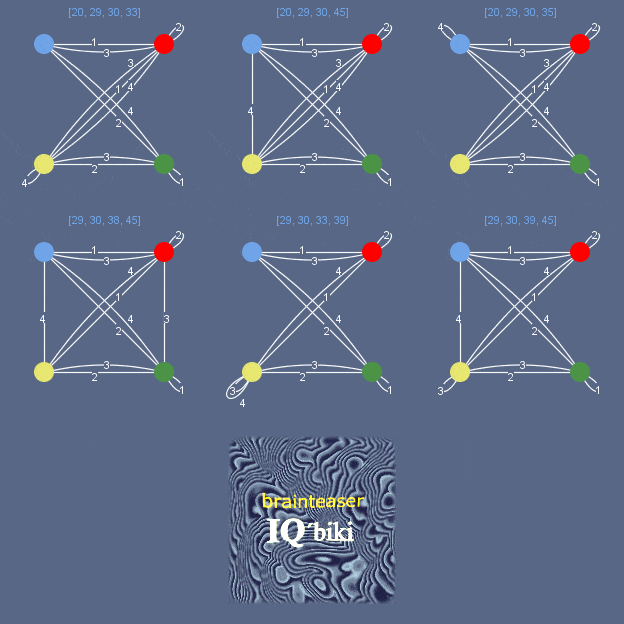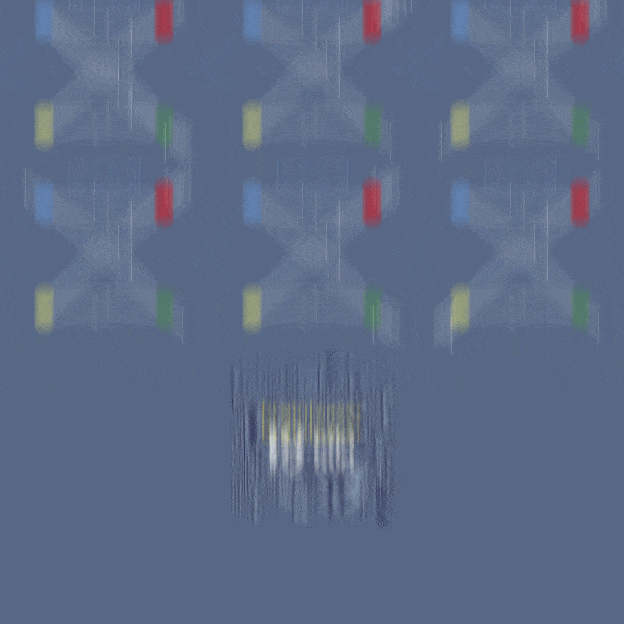
Рис. 4. 204 графа «головоломки с четырьмя цветными кубиками».

Изоморфизм

Я питаю лишь небольшую надежду, что кто-то вглядывался внимательно в приведенные мной графы – заметьте – для всех! головоломок из четырех цветных кубиков, и, кроме того, удосужился разглядеть внимательно графы решений для Instant Insanity и её клонов с сайта Роберта Штегманна. Между тем, у этого пытливого гипотетического читателя несомненно возник бы вопрос: «А где же, где этот самый, растиражированный миллионами экземпляров, граф Instant Insanity? — Совсем ничего похожего ни на одном из этих графов?» – А он, тем не менее, есть… Однако, не удивительно, что узнать этот граф не удается с первого раза – тут я, впрочем, погорячился: со второго или третьего узнать этот граф тоже шансов нет – эта проблема зовется изоморфизмом графов.

 

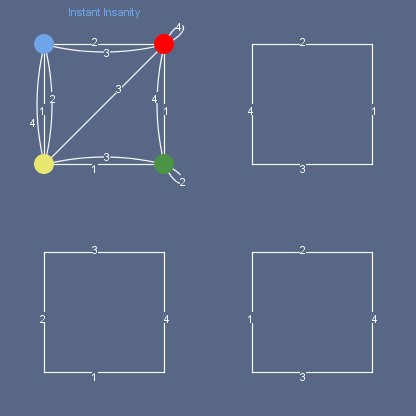Граф Instant Insanity и бесчисленного числа её клонов, застенчиво наделенных их «создателями» разными именами, можно видеть на левом рисунке. Обычно именно этим рисунком сопровождается продаваемый экземпляр головоломки для поддержания духа в совсем отчаявшихся… (Уже сделанное мною разбиение на подграфы, надо надеяться, снимет вообще все их затруднения) Узнать в приведенном ниже рисунке эту головоломку невозможно – а это лишь одна из 1073 возможных головоломок из четырех кубиков!, просто перекрашенная (и, вероятно, где-то существующая с другим названием).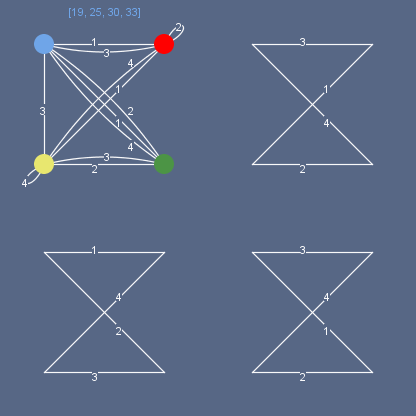


Есть различные способы выявления изоморфизма графов, но описание любого из них, по моему мнению, избыточно для и без того затянувшейся статьи. Однако, без иллюстрации к «чуду превращения» некоторая часть читателей может счесть себя разочарованной, а я предпочитаю, чтобы она нашла себе для этого другие причины.

Возьмем развертку головоломки Instant Insanity на сайте Роберта Штегманна (R.Stegmann – он то, наверное, «рукопожатый» всем клубом IPP!) — я буду придерживаться следующего порядка обхода граней кубика: нижняя грань→лицевая→верхняя→задняя→левая→правая.

Самая распространенная из разверток с отмеченного сайта (автором собрано и несколько клонов, но мы ориентируемся на «классический» вариант головоломки) будет в выбранном порядке обхода граней записана следующим образом: RWGGWB, RBBWGG, RGWWRB, GWRBRR.
Надеюсь, что никому не удалось забыть, что при записи графа мы принимаем во внимание лишь пары цветов противоположных граней, и поэтому строчная запись графической конфигурации выбранных кубиков выглядит не иначе, чем: RG|WG|WB, RB|BW|GG, RW|GW|RB, GR|WB|RR. Как видим, мультиграф на первом рисунке полностью соответствует этому набору (ну лишь за исключением, что у меня желтый цвет вместо классического белого).

Возможно, не одному мне удобнее работать с цифрами, поэтому обозначим цифрами цвета (и исключим тем самым некоторое замеченное выше несогласие в цветах), а заодно запишем эту комбинацию кубиков сразу в положении решения (благо, что два подграфа, указывающие нам путь, у нас перед глазами):

• R=0, W=1, B=2, G=3
• После чего, заменим цвета («перекрасим кубики») следующим образом:
  0→1, 1→2, 2→3, 3→0
• и в завершении каждый из них дважды повернем на 90 градусов вокруг «длинной» оси пирамиды (в принятых в предыдущей публикации терминах, это равнозначно перестановке граней в порядке 230145,– это, конечно, уже не цвета, а индексы)

[0, 1, 3, 3, 1, 2] → [1, 2, 0, 0, 2, 3] → [0, 0, 1, 2, 2, 3] : RW|RB|BG
[2, 2, 0, 1, 3, 3] → [3, 3, 1, 2, 0, 0] → [1, 2, 3, 3, 0, 0] : WG|BG|RR
[3, 0, 1, 2, 0, 1] → [0, 1, 2, 3, 1, 2] → [2, 3, 0, 1, 1, 2] : BR|GW|WB
[1, 3, 2, 0, 0, 0] → [2, 0, 3, 1, 1, 1] → [3, 1, 2, 0, 1, 1] : GB|WR|WW

Можно сравнить получившийся граф с тем, что помещен ниже графа Instant Insanity, и убедиться, что он это один и тот же граф.

Вместо заключения

Очень надеюсь, что чтение не было скучным. Возможно, кому-то оказалось отчасти полезным. И практически уверен, что количество нарисованных конвертиков к завтрашнему дню несколько возрастет, и кто-то наконец найдет в себе силы и мотивацию отвлечь наследника от его гаджета какой-нибудь занимательной и умной задачей. Эйлер вот не пренебрегал…

---

1.↑Леонард Эйлер. Письма к ученым, Издательство АН СССР, 1963, стр.339
2.↑Леонард Эйлер. Письма к ученым, Издательство АН СССР, 1963, стр.153
3.↑Генри Э. Дьюдени. 520 головоломок. Составитель и редактор американского издания М. Гарднер, Издательство МИР, Москва, 1975

---

Ответы на вопросы опроса

Полагаю, что все, кто хотел, в опросе уже поучаствовали, поэтому можно и пора разместить ответы.

1. Сколько путей обхода удалось найти у головоломки «Конверт»?
   Если вы обозначите самую верхнюю точку «конверта» буквой «А», а остальные узлы, в любом направлении обхода, обозначите в порядке BCDE, то начав с узла С, получите следующие 44 -е маршрута:
   CBAEBDCED CBEABDECD CDEABCEBD CEABEDCBD
CBAEBDECD CBECDBAED CDEABECBD CEBAEDBCD
CBAECDBED CBECDEABD CDEBAECBD CEBAEDCBD
CBAECDEBD CBEDBAECD CDEBCEABD CEBCDBAED
CBAEDBECD CBEDCEABD CDECBAEBD CEBCDEABD
CBAEDCEBD CDBAEBCED CDECBEABD CEBDCBAED
CBDCEABED CDBAECBED CEABCDBED CEBDEABCD
CBDCEBAED CDBCEABED CEABCDEBD CEDBAEBCD
CBDEABECD CDBCEBAED CEABDCBED CEDBEABCD
CBDEBAECD CDBEABCED CEABDEBCD CEDCBAEBD
CBEABDCED CDBECBAED CEABEDBCD CEDCBEABD
начав с узла D, вы их обойдете в обратную сторону.
   Правильный ответ: «88».
   
2. Где нужно достроить мост на графе Кёнигсбергских мостов, чтобы к удовольствию любителей пеших прогулок они дважды не проходили одним маршрутом?
   Узлы графа имеют следующую четность: A — 5, B — 3, C — 3, D — 3.
   Любые два узла, которые будут соединены ребром, увеличат свою четность на единицу, т.е. нечетными останутся два других узла, любой из которых можно брать началом маршрута, завершением этого марщрута послужит оставшийся нечетный узел.
   Правильный ответ: «да стройте, где хотите!».
   
3. Какой из графов на картинке соответствует развертке кубов?
   
   
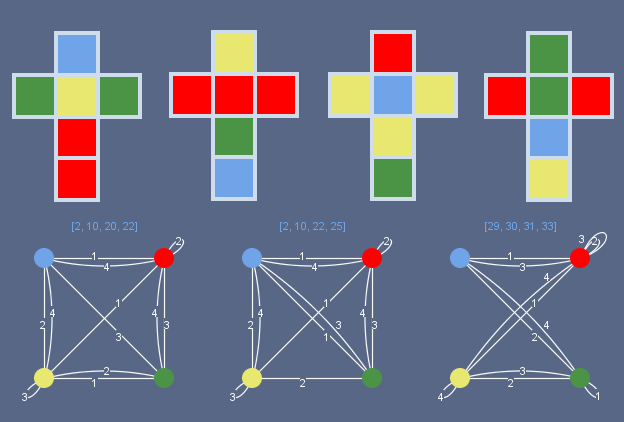
   Развертки кубов переставлены в порядке 1342. Соответствующий разверткам мультиграф размещен третьим среди графов задачи.
   Правильный ответ: «третий».