maisvendoo Feb 17 2018 at 17:28

Моделирование динамических систем: задача внешней баллистики

9 min

31K

Tutorial

Введение

Надеюсь что мы с вами набрались достаточно опыта, чтобы смоделировать что-нибудь более серьезное, чем полет камня. Предлагаю такую задачу

Пушка, стреляющая сферическими ядрами сообщает им начальную скорость 400 м/с. Определить траекторию полета снаряда при стрельбе под углом в 35 градусов к горизонту. Поле силы тяжести считать однородным, кривизной Земли пренебречь.

Надо сказать, это пример некорректно поставленной задачи. Во-первых, не сказано учитываем мы, или не учитываем сопротивление воздуха. А если учитываем, то в задаче явно не хватает параметров. К сожалению такого рода постановка задач весьма распространенное явление. Поэтому мы решим задачу для обоих случаев, а нужные параметры введем в неё сами. Заодно научимся чему-то новому. Поехали!

1. Расчетная схема

В прошлые разы я сознательно не рисовал никаких схем, чтобы потренировать ваше воображение. Несложно представить себе камень, падающий вертикально вниз. Сейчас задачка посложнее, и без чертежа нам не обойтись.

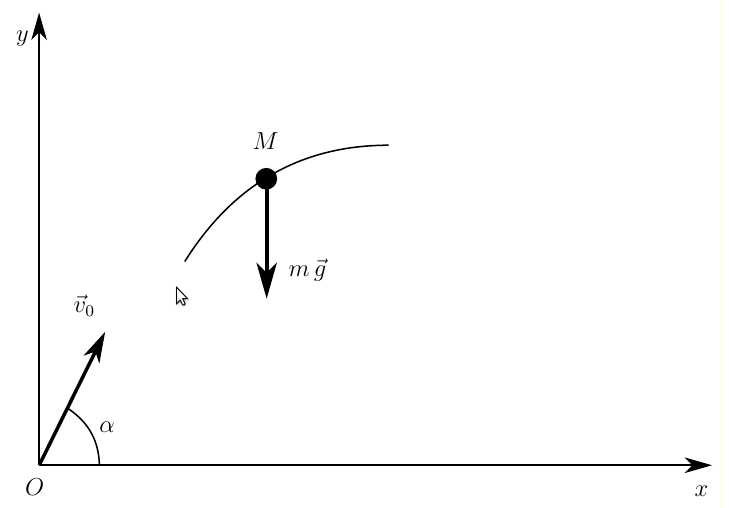
Подобные чертежи называют расчетной схемой — условным графическим изображением процесса или объекта, выполненным с учетом введенных в задачу допущений.

Обратите внимание, что на схеме нарисовано произвольное положение снаряда, то, в которое он попадет по истечении некоторого времени от начала движения. В задачах динамики так удобнее представить себе взаимное расположение векторов сил и правильно разложить их на осевые проекции. Единственное, что мы показали в начальном положении — вектор начальной скорости. Это пригодится при задании начальных условий.

2. Формализация задачи (без учета сопротивления среды)

Все готово к составлению системы дифференциальных уравнений движения

$\begin{align} &m \, \ddot x = 0 \\ &m \, \ddot y = -m\,g \end{align}$

Мы не учитываем сопротивления воздуха, и у нас всего одна сила: на ось x она проецируется в ноль, на ось y — в истинную величину с минусом. Ведь мы приняли допущение, что поле силы тяжести однородно а Земля плоская. Значит сила тяжести всегда постоянна и направлена вертикально вниз. Как видно, от массы тут ничего не зависит, масса сокращается в обоих уравнениях

$\begin{align} &\ddot x = 0 \\ &\ddot y = -g \end{align}$

Получилась система двух уравнений второго порядка. Нам нужно привести её к форме Коши. Помните что это? Если помните, попробуйте сделать это сами, не заглядывая под спойлер

Ответ

Все просто, производные координат, это соответствующие проекции скорости

$\begin{align} &\dot x = v_x \\ &\dot y = v_y \end{align}$

а проекции ускорения — производные от проекций скорости

$\begin{align} &\ddot x = \dot v_x \\ &\ddot y = \dot v_y \end{align}$

Получаем систему уравнений в форме Коши

$\begin{align} &\dot x = v_x \\ &\dot y = v_y \\ &\dot v_x = 0 \\ &\dot v_y = -g \end{align}$

3. Скрипты Octave, или как заново не делать одну и ту же работу

В прошлый раз мы вводили команды в прямо в консоли Octave. Хорошо задачка у нас была маленькая. А если большая? А если хочется поменять параметры? А если хочется вернуться к отложенной работе? А если… Короче говоря, хорошо иметь возможность сохранять свои программы на Octave. И таки тут нет ничего невозможного.

Внизу экрана, под командным окном есть вкладки: Command Window, Editor и Documentation. Вкладка Editor — то что нам нужно. Это редактор скриптов на m-языке. Откроем эту вкладку и введем в неё такой текст

%-------------------------------------------------------------------------------
%
%   Баллистическая задача без учета сопротивления среды
%   система ОДУ движения
%
%-------------------------------------------------------------------------------
function dYdt = f(Y, t)

  g = 9.81; % Ускорение свободного падения

  dYdt(1) = Y(3); % dx/dt = vx
  dYdt(2) = Y(4); % dy/dt = vy
  dYdt(3) = 0;    % dvx/dt = 0
  dYdt(4) = -g;   % dvy/dt = -g
  
endfunction

Это ничто иное, как правая часть системы дифференциальных уравнений движения снаряда, в нашей задаче, оформленная в виде функции на m-языке. Смысл тот же самый что и прошлый раз. Только теперь уравнений у нас аж четыре. Ну и ускорение свободного падения берем уже нормальной, взрослой величины. Сохраним этот файл на диске под именем f.m

Внимание! Каждая функция на m-языке требует сохранения в собственный файл, имя которого совпадает с именем функции. В нашем случае функция имеет имя f, значит и файл имеет имя f.

Для тех, кто использует Windows

В нормальных операционных системах файловая система отличает буквы верхнего и нижнего регистров. Windows же до сих пор этому не научилась, по крайней мере в командной строке. Поэтому функциям лучше давать имена в нижнем регистре.

Что за строки, начинающиеся с "%"? А это, братья-апачи, комментарии! Текст, предваренный этим символом в Octave игнорируется интерпретатором. Комментариями не только можно, но и нужно снабжать свои программы, чтобы хотя бы самому в них ориентироваться, не говоря уже о других людях, желающих воспользоваться вашей программой.

Итак, мы задали октаве систему уравнений. Создадим новый файл, назовем его, например, ballistics.m и сохраним там же, где и сохранили предыдущий файл. Начнем решать задачу!

%-------------------------------------------------------------------------------
% Параметры стрельбы
%-------------------------------------------------------------------------------

% начальная скорость снаряда
v0 = 400; 
% угол наклона ствола пушки к горизонту
alpha = 35 * pi / 180; 

%-------------------------------------------------------------------------------
% Начальные условия
%-------------------------------------------------------------------------------
x0 = 0;
y0 = 0;
vx0 = v0 * cos(alpha);
vy0 = v0 * sin(alpha);

Y0 = [x0; y0; vx0; vy0];

%-------------------------------------------------------------------------------
% Параметры временного интервала
%-------------------------------------------------------------------------------

% начальный момент времени
t0 = 0;
% конечный момент времени
tend = 10.0;
% шаг выдачи решения
deltaT = 0.1;

% Массив интересующих нас моментов времени
t = [t0:deltaT:tend];

% Интрегрируем систему уравнений движения
Y = lsode("f", Y0, t);

% Рисуем траекторию полета снаряда
plot(Y(:,1), Y(:,2));

Смысл большинства операций понятен из комментариев. Отдельно поясню начальные условия. У нас четыре фазовых координаты: две декартовы координаты снаряда, две проекции его скорости на оси координат

$\begin{align} &Y(1) \to x(t) \\ &Y(2) \to y(t) \\ &Y(3) \to v_x(t) \\ &Y(4) \to v_y(t) \end{align}$

Для каждой из фазовых координат нужно задать их начальное значение. Логично задать начальное положение в начале координат. Что качается двух других переменных, то это, внимание, начальные величины проекций вектора скорости на оси x и y. Затем я и нарисовал вектор начальной скорости, чтобы легко было найти его проекции на оси

$\begin{align} &v_x = v_0 \, \cos \alpha \\ &v_y = v_0 \, \sin \alpha \\ \end{align}$

Теперь всё готово. Жмем на кнопку с шестерней и желтым треугольником, чтобы запустить скрипт. В ответ система выдаст окошко

попросит нас добавить путь, по которому лежит скрипт в пути поиска скриптов. Это нужно сделать один раз после загрузки скрипта в редактор или создании нового скрипта. Жмем кнопку «Add...» и получаем результат

Выглядит многообещающе. Время 10 секунд мало, чтобы наряд приземлился. Меняем значение tend и запускаем скрипт снова, пока не получим похожую картинку

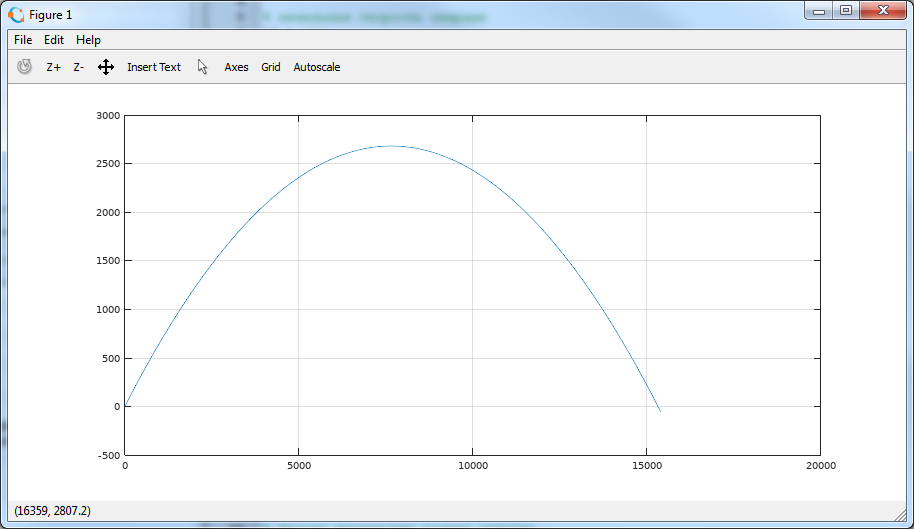
соответствующую tend = 47 секунд. Симуляция закончилась, снаряд пролетел ниже оси x, но это нормально, ведь мы никак не моделируем его встречу с поверхностью.

4. Формализация задачи (с учетом сопротивления среды)

Шар в качестве формы снаряда мы выбрали не случайно. Как его не верти, со всех сторон у него одинаковое сечение — круг (кстати, то той же причина КК «Восток» имел шарообразную форму спускаемого аппарата). А значит, как ни направляй поток воздуха, при обтекании сила сопротивления движению будет одинакова и равна

$R = c_f \, S \, \frac{\rho \, v^2}{2}$

где c_f = 0.47 — коэффициент лобового сопротивления формы; S — площадь поперечного сечения; $\rho$ = 1.29 кг/м³ — плотность воздуха; v — скорость набегающего потока, в нашем случае скорость снаряда.

Вектор силы сопротивления всегда будет направлен против вектора скорости. Поэтому перерисуем расчетную схему

Как учесть тот факт, что для любого момента времени вектор $\vec R$ направлен против скорости? Очень просто. Мы знаем, что вектор скорости направлен по касательной к траектории. Введем вектор $\vec\tau$ с длинной равной 1 и направленные туда же, куда направлена скорость. Тогда вектор $\vec R$ можно выразить через вектор $\vec\tau$ и модуль силы сопротивления

$\vec R = - R \, \vec\tau$

А как найти вектор $\vec\tau$ ? Очень просто, его проекции на оси координат будут равны

$\begin{align} \tau_x = \frac{v_x}{v} \\ \tau_y = \frac{v_y}{v} \end{align}$

Модуль вектора скорости легко выражается через его проекции

$v = \sqrt{v_x^2 + v_y^2}$

Тогда проекции вектора силы сопротивления воздуха на оси координат легко посчитать

$\begin{align} &R_x = - R \, \tau_x = -R \, \frac{v_x}{v} = - \frac{1}{2} \, c_f \, S \, \rho \, v \, v_x \\ &R_y = - R \, \tau_y = -R \, \frac{v_y}{v} = - \frac{1}{2} \, c_f \, S \, \rho \, v \, v_y \\ \end{align}$

И это меняет уравнения движения

$\begin{align} &m \, \ddot x = - \frac{1}{2} \, c_f \, S \, \rho \, v \, v_x \\ &m \, \ddot y = - \frac{1}{2} \, c_f \, S \, \rho \, v \, v_y - m \, g \end{align}$

Это что же выходит, массу теперь не сократить? Да, теперь динамика полета снаряда будет зависеть от массы. Но на массу никто не запрещает делить, делим на неё оба уравнения

$\begin{align} &\ddot x = - k \, v \, v_x \\ &\ddot y = - k \, v \, v_y - g \end{align}$

где

$k = \frac{c_f \, S \, \rho}{2 \,m}$

коэффициент, определяющий вклад силы сопротивления в ускорение снаряда. Его можно сильно упростить, если вспомнить, что снаряд — шар

$m = \gamma \, V = \gamma \, \frac{4}{3} \, \pi \, r^3, \quad S = \pi \, r^2$

Первая формула — масса шара, и тут $\gamma$ — плотность материала, из которого сделано ядро, а r — радиус ядра. Вторая формула — площадь поперечного сечения шара. Подставим эти формулы в выражение для коэффициента и упростим

$k = c_f \, \rho \frac{\pi \, r^2}{\frac{8}{3} \, \gamma \, \pi \, r^3} = \frac{3}{8} \, \frac{c_f \, \rho}{r \, \gamma} = \frac{3}{4} \, \frac{c_f \, \rho}{d \, \gamma}$

где d — диаметр ядра, калибр нашей пушки. Из этой формулы уже видно, что чем больше будет калибр и плотнее материал снаряда, тем меньше будет влияние силы сопротивления воздуха.

Зададимся значениями параметров снаряда. Добавим в конец файла ballistics.m следующие строки

%-------------------------------------------------------------------------------
% Параметры снаряда
%-------------------------------------------------------------------------------

% плотность материала снаряда
global gamma = 7800; 
% коэффициент сопростивления формы (для шара)
global c_f = 0.47;
% калибр
global d = 0.1;

Пускай ядро будет чугунным калибра 100 мм. Что за слово такое, global перед каждой из переменных. Таким образом мы говорим системе, что созданные переменные будут доступны для всех скриптов и определенных в них функций, то есть будут глобальными.

Остается записать для Octave построенную нами модель в виде функции, пусть это будет функция f_air. Естественно, для неё нужно создать отдельный файл f_air.m. Попробуйте провернуть это самостоятельно. Дам подсказку: начале тела этой функции следует определить ещё раз наши глобальные параметры снаряда, но уже без значений. Это необходимо, чтобы функция видела глобальные переменные

global c_f;
global gamma;
global d;

Если будут совсем трудно, загляните под спойлер.

Приведение к форме Коши и функция f_air

С приведением к форме Коши всё просто. Вот исходная система уравнений

$\begin{align} &\ddot x = - k \, v \, v_x \\ &\ddot y = - k \, v \, v_y - g \end{align}$

Первые производные координат есть проекции скорости

$\dot x = v_x \quad \dot y = v_y$

Соответственно

$\ddot x = \dot v_x \quad \ddot y = \dot v_y$

что дает систему уравнений

$\begin{align} &\dot x = v_x \\ &\dot y = v_y \\ &\dot v_x = - k \, v \, v_x \\ &\dot v_y = - k \, v \, v_y - g \end{align}$

function dYdt = f_air(Y, t)
  
  global c_f;
  global gamma;
  global d; 
 
  % Ускорение свободного падения
  g = 9.81;
  
  % Плотность воздуха
  rho = 1.29;
  
  % Коэффициент сопротивления снаряда
  k = 3 * c_f * rho / 4 / gamma / d;
 
  % Модуль скорости снаряда
  v = sqrt(Y(3) * Y(3) + Y(4) * Y(4));  
  
  % Система уравнений движения
  dYdt(1) = Y(3);
  dYdt(2) = Y(4);
  dYdt(3) = - k * v * Y(3);
  dYdt(4) = - k * v* Y(4) - g;
 
endfunction

Теперь решаем систему уравнений движения, в файле ballistics.m даем команды

Y_air = lsode("f_air", Y0, t);
plot(Y_air(:,1), Y_air(:,2));

то есть интегрируем новые уравнения движения с теми же начальными условиями и на том же временном интервале, что и для задачи без учета сопротивления воздуха, а так же рисуем график траектории

Ого, максимальная высота полета уменьшилась весьма существенно. И 47 секунд теперь слишком большой диапазон, снаряд падает на землю намного раньше. Поиграем со временем

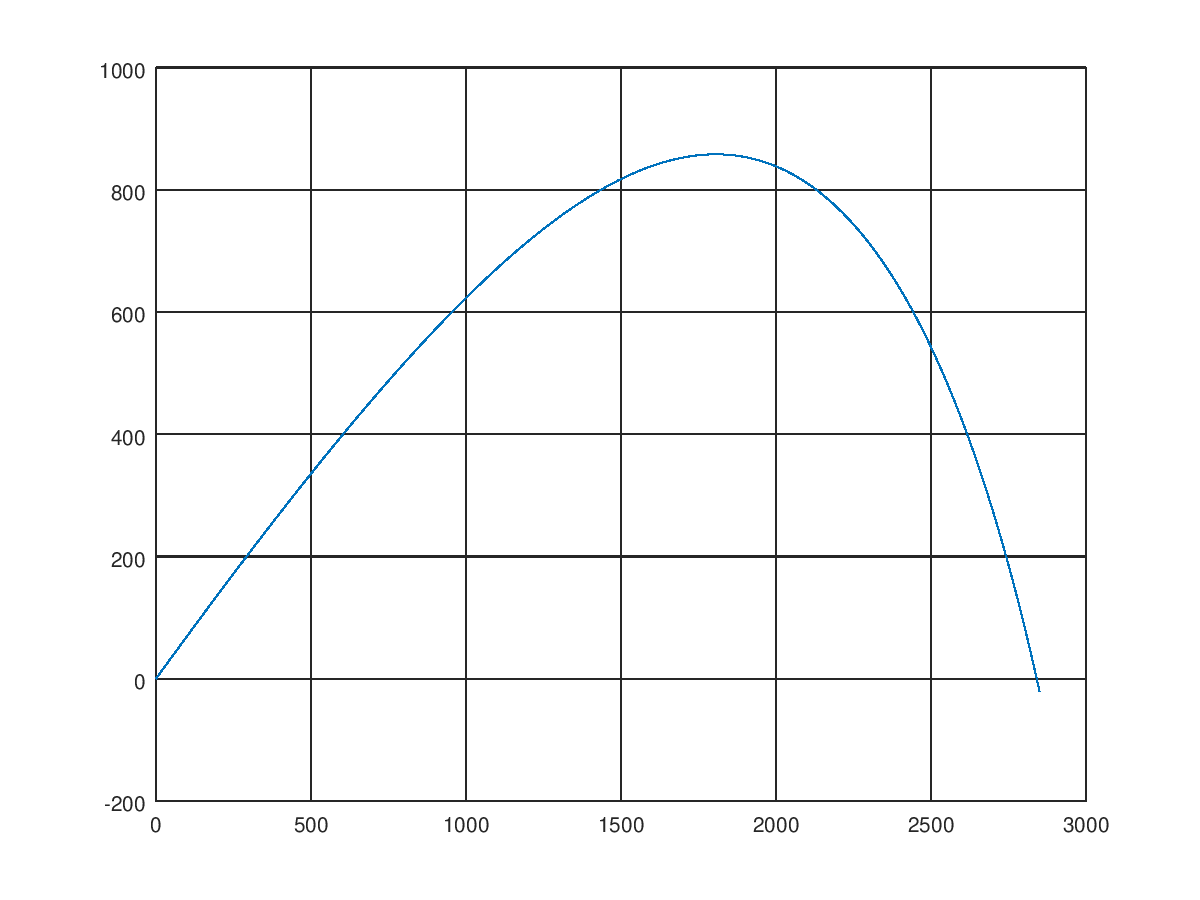
При tend = 26 секунды видим, что и дальность полета весьма значительно. Видно, что аэродинамическое сопротивление очень существенно влияет на характеристики нашего орудия и в реальности пренебрегать им нельзя. Меняется и форма траектории: она более полога на восходящем участке, и круто идет вниз на нисходящем, мало напоминая идеальную параболу.

5. Сравнение траекторий снаряда

Мы уже видим, что результаты моделирования полета ядра различаются между собой. Но всё познается в наглядном сравнении. Построим две траектории одновременно. Можно? Да проще простого

% Строим обе траектории
plot(Y_air(:,1), Y_air(:,2), Y(:,1), Y(:,2));

Сначала мы указали абсциссу и ординату для одной траектории, потом для другой. Что получилось?

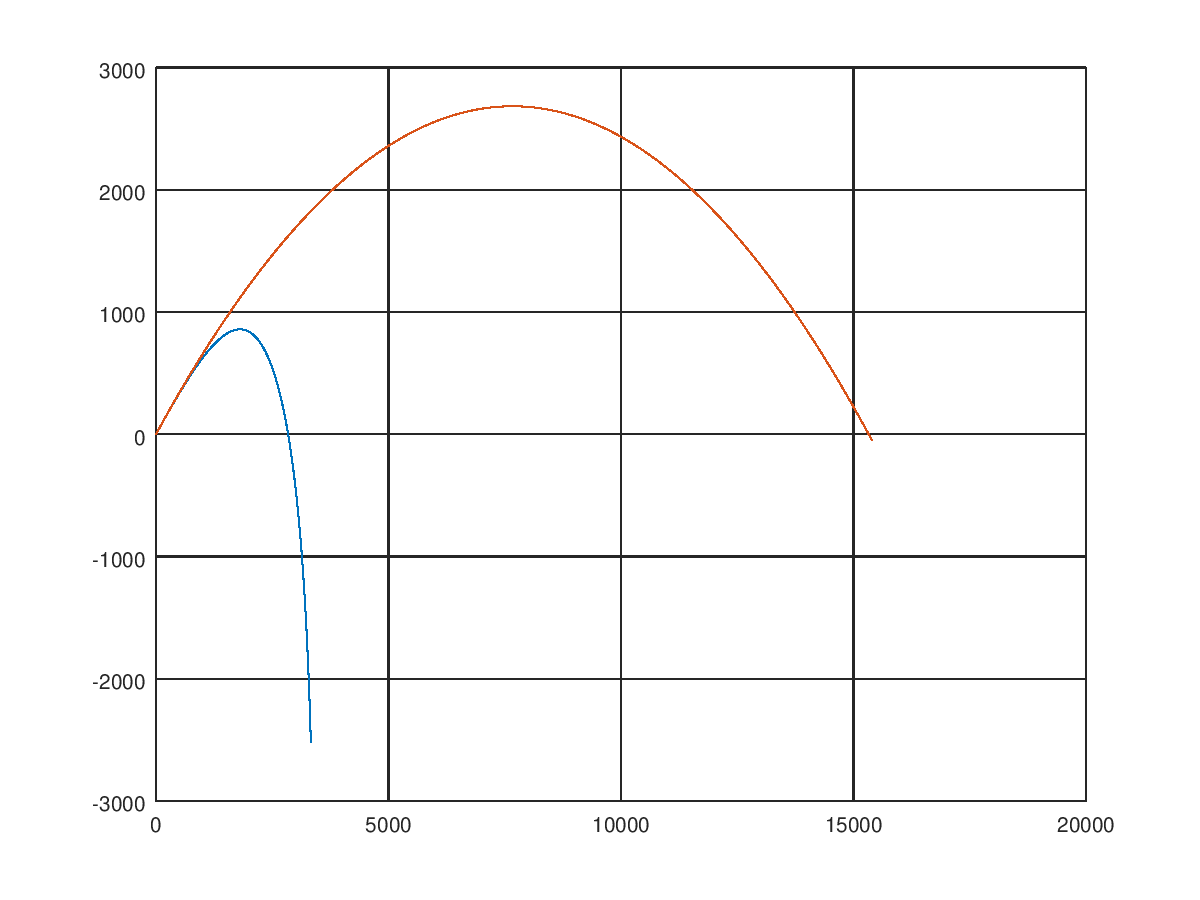
Эмм, это какой-то бред. Правильно, время полета снаряда в разных решениях разное. Столкновение ядра с поверхностью мы не моделируем. Из этой ситуации можно выкрутится, задав пределы изменения координат по осям командной axis(), вот так

% Задаем пределы отображения графиков по осям координат
xmin = 0;
xmax = 16000;
ymin = 0;
ymax = 3000;

axis([xmin xmax ymin ymax], "manual");

Теперь графики будут выглядеть так

Уже лучше. По крайней мере траектории можно сравнить между собой. А если нам хочется, чтобы по всем осям графика был одинаковый масштаб? Гугление дало такую команду

set(gca,'dataaspectratio',[1 1 1]);

определяющий одинаковый масштаб осей графика по всем осям координат

Под спойлером полный текст файла ballistics.m

ballistics.m

%-------------------------------------------------------------------------------
% Параметры стрельбы
%-------------------------------------------------------------------------------

% начальная скорость снаряда
v0 = 400; 
% угол наклона ствола пушки к горизонту
alpha = 35 * pi / 180; 

%-------------------------------------------------------------------------------
% Начальные условия
%-------------------------------------------------------------------------------
x0 = 0;
y0 = 0;
vx0 = v0 * cos(alpha);
vy0 = v0 * sin(alpha);

Y0 = [x0; y0; vx0; vy0];

%-------------------------------------------------------------------------------
% Параметры временного интервала
%-------------------------------------------------------------------------------

% начальный момент времени
t0 = 0;
% конечный момент времени
tend = 47.0;
% шаг выдачи решения
deltaT = 0.1;

% Массив интересующих нас моментов времени
t = [t0:deltaT:tend];

% Интрегрируем систему уравнений движения
Y = lsode("f", Y0, t);

%-------------------------------------------------------------------------------
% Параметры снаряда
%-------------------------------------------------------------------------------

% плотность материала снаряда
global gamma = 7800; 
% коэффициент сопростивления формы (для шара)
global c_f = 0.47;
% калибр
global d = 0.1;

% Интегрируем систему уравнений движения 
Y_air = lsode("f_air", Y0, t);

% Строим обе траектории
plot(Y_air(:,1), Y_air(:,2), Y(:,1), Y(:,2));

% Задаем пределы отображения графиков по осям координт
xmin = 0;
xmax = 16000;
ymin = 0;
ymax = 3000;

axis([xmin xmax ymin ymax]);

% Задаем масштаб по осям
set(gca,'dataaspectratio',[1 1 1]);

Заключение

В рассмотренном нами примере мы столкнулись с фундаментальным свойством законов природы — они нелинейны. Если учитывать сопротивление воздуха, то правые в части дифференциальных уравнений фазовые координаты входят нелинейно. Аналитического решения, то есть выраженного в элементарных функциях задача не имеет. Наличие аналитического решения для реальных задач техники скорее исключение. И без моделирования при их решении уже никак не обойтись.

Но само по себе решение уравнений движения на практике имеет мало смысла. Что нам дало это решение? Да, мы увидели влияние силы сопротивления воздуха на полет пушечного ядра. Но мы, например, не ответили на многие вопросы, например, какова точная дальность стрельбы нашей пушки? Какова максимальная высота подъема снаряда? Под каким углом надо стрелять, чтобы достичь максимальной дальности?

Математические модели создают для того, чтобы решать с помощью них практические задачи техники. Вот об этом мы и поговорим в следующий раз.

P.S.: Проекты примеров теперь будут доступны на Github

Tags:

Octave; моделирование; механика

Hubs: