
«Имеются два одинаковых шарика, находящихся при одной и той же температуре. Один из них лежит на горизонтальной поверхности, другой подвешен на нити. Обоим шарикам сообщают одинаковое количество теплоты. Будут ли после этого температуры шариков одинаковыми или нет? (Любыми видами тепловых потерь можно пренебречь.)»
Такую задачу иногда можно встретить на олимпиадах по физике или в соцсетях. Общепринятый ответ интуитивно понятен: из-за затрат энергии на тепловое расширение при наличии силы тяжести шарик, лежащий на горизонтальной поверхности, окажется холоднее висящего на нити. В недавней статье было показано, что этот ответ неправильный. На самом деле, результат будет обратным: лежащий шарик окажется теплее висящего. Разберемся, почему традиционный метод решения этой задачи приводит к неправильному ответу, и почему интуиция в этом случае нас подводит.
Традиционное решение и его проблема
Традиционное решение основано на следующей цепочке рассуждений. Оба шарика при нагреве будут расширяться, из-за этого у шарика, лежащего на горизонтальной поверхности, центр масс немного поднимется, а у висящего шарика центр масс опустится. В результате лежащий шарик нагреется слабее, поскольку часть переданной ему теплоты будет затрачена на его подъем, а висящий шарик нагреется сильнее за счет дополнительной работы силы тяжести при его опускании.

Рассуждения, используемые при традиционном решении: из-за теплового расширения лежащий на столе шарик поднимается, а висящий на нити шарик опускается.
Ответ можно выразить простой формулой для разности температур лежащего (
Казалось бы, в этом решении все логично. «Первой ласточкой», демонстрирующей, что здесь что-то не так, является мысленная попытка создать на основе шарика тепловую машину.
Машина может работать следующим образом: сначала шарик лежит на столе, где мы его нагреваем, из-за чего его центр масс поднимается. Затем мы закрепляем шарик на висящей сверху нити и аккуратно убираем стол, так, чтобы высота шарика не изменилась. Наконец, охлаждаем шарик до его первоначальной температуры, в результате шарик сожмется и его центр масс поднимется. Итог: часть теплоты, которую мы передавали шарику при его нагреве, превратилась в механическую работу по его подъему, и этот цикл можно бесконечно повторять.
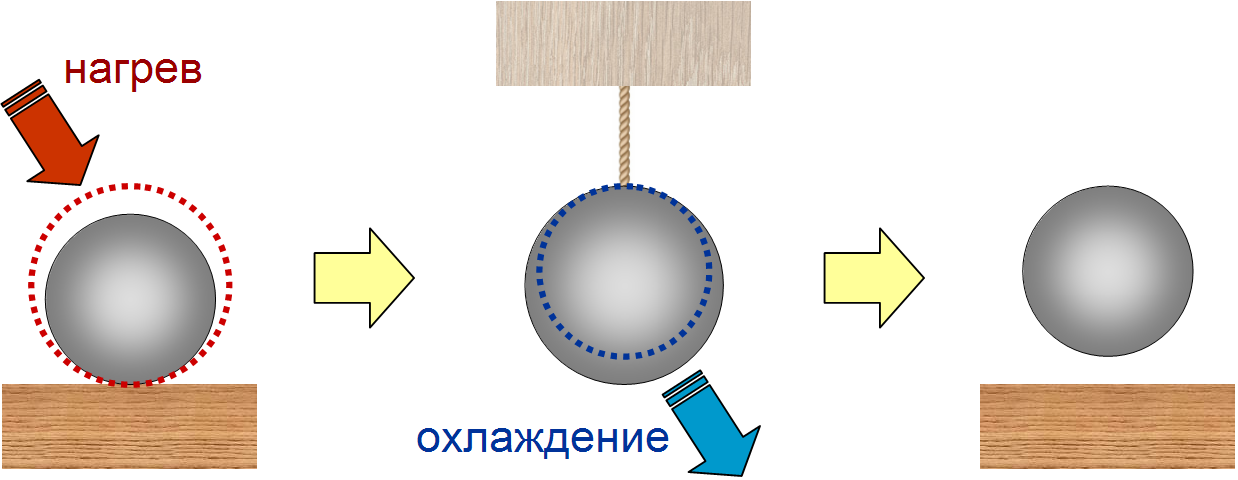
Цикл работы тепловой машины на основе шарика: после нагрева и охлаждения шарик поднялся, а это значит, что часть теплоты мы превратили в механическую работу.
Проблема здесь в том, что, увеличивая радиус шарика, коэффициент полезного действия (КПД) такой машины можно сделать сколь угодно близким к 100%. Это противоречит второму началу термодинамики, согласно которому КПД тепловой машины не может превышать КПД цикла Карно при тех же температурах нагревателя и холодильника.
В чем же дело?
Почему же традиционное решение задачи оказывается неправильным? Здесь нужно учесть, что лежащий на столе шарик уже с самого начала, до его нагрева, будет немного сплющен под действием силы тяжести, а висящий шарик будет немного растянут. Это отрицательно скажется на эффективности вышеописанной тепловой машины: в процессе подвешивания шарик будет слегка опускаться, из-за этого КПД снизится и уже не будет превышать КПД цикла Карно.

Влияние силы тяжести на шарики: лежащий на столе шарик сплющивается, а висящий на нити — растягивается.
Как это проявится при рассмотрении исходной задачи? Оказывается, сжатие или растяжение материала меняет его теплоемкость: в случае сжатого материала нагрев на ту же температуру потребует меньшего количества теплоты, чем в случае растянутого. Следовательно:
- При нагреве шарика, лежащего на столе, часть теплоты уйдет на его подъем за счет теплового расширения; но, вместе с этим, нагрев самого материала шарика будет происходить легче и потребует меньше теплоты.
- При нагреве шарика, висящего на нити, работа силы тяжести при его опускании добавится к переданной ему теплоте; но, вместе с этим, нагрев самого материала шарика будет более трудоемким и потребует больше теплоты.

При традиционном решении учитываются только факторы, обозначенные белыми стрелочками. Игнорирование факторов, показанных черными стрелочками, приводит к ошибочному ответу.
Как мы видим, в обоих случаях есть факторы, работающие как в пользу одного варианта ответа (лежащий шарик может оказаться холоднее висящего), так и в противоположную сторону (лежащий шарик может оказаться теплее висящего). Какой из них пересиливает?
Казалось бы, эффект изменения теплоемкости материала при его сжатии или растяжении, даже если и существует, должен быть очень мал, и им можно пренебречь, как и делается при традиционном решении задачи. Однако это не так. Этот эффект такого же порядка малости, что и само тепловое расширение, поскольку оба этих эффекта проистекают из ангармонизма межатомных сил. Учет одного из этих эффектов при традиционном решении в сочетании с игнорированием другого непоследователен и приводит к ошибочному ответу.
В статье показывается, что при правильном решении задачи разность температур шариков после передачи им одинакового количества теплоты оказывается равной:
По сравнению с результатом традиционного решения, разность температур оказывается:
- Противоположного знака, так как для большинства материалов величина
положительна, поэтому вся правая часть равенства тоже положительна, и
.
- Гораздо меньшей по абсолютной величине, так как здесь вместо малой величины фигурируют еще более малые величины
и
.
Таким образом, два рассмотренных выше эффекта почти полностью компенсируют друг друга, но второй из них (изменение теплоемкости при сжатии или растяжении) оказывается немного сильнее первого (теплового расширения).
Ангармонизм межатомных сил
Авторы статьи проводят достаточно строгое рассмотрение задачи, но, к сожалению, не дают наглядного объяснения того, как именно происходит почти полная компенсация двух эффектов, поэтому в этом вопросе пришлось разбираться самому.
На рисунке изображена типичная зависимость потенциальной энергии взаимодействия атомов от расстояния между ними. Действующая на атомы сила направлена в сторону убывания потенциальной энергии, поэтому атомы сильно отталкиваются друг от друга на малых расстояниях и слабо притягиваются на больших расстояниях. На некотором расстоянии
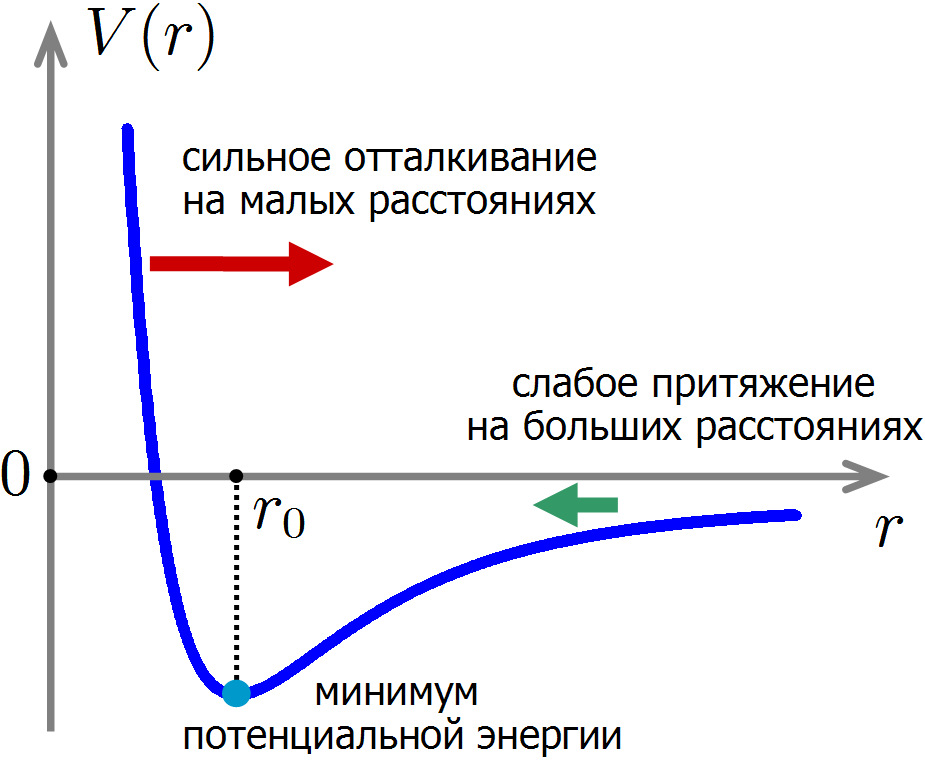
Теперь разберемся, откуда возникает тепловое расширение материалов. При хаотичном тепловом движении расстояние между атомами уже не равно строго
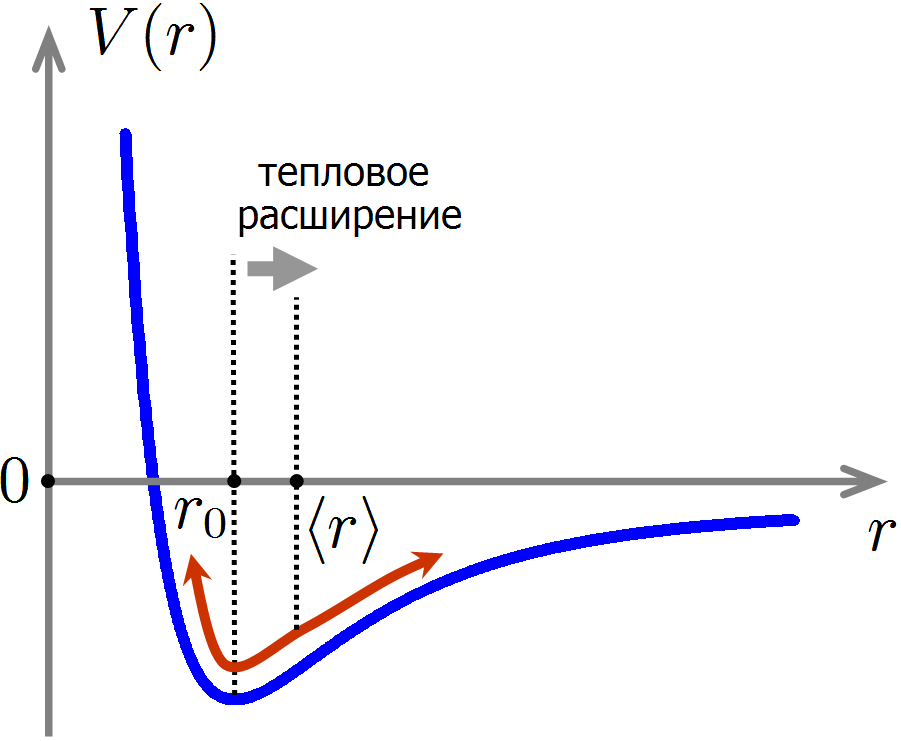
Причина теплового расширения материалов: при тепловом движении среднее расстояние между атомами увеличивается за счет ангармонизма сил межатомного взаимодействия.
Что происходит при сжатии или растяжении материала, как в случае сплющенного или растянутого шариков? При сжатии материала внешняя сила уменьшает среднее расстояние между атомами, а при растяжении — увеличивает.
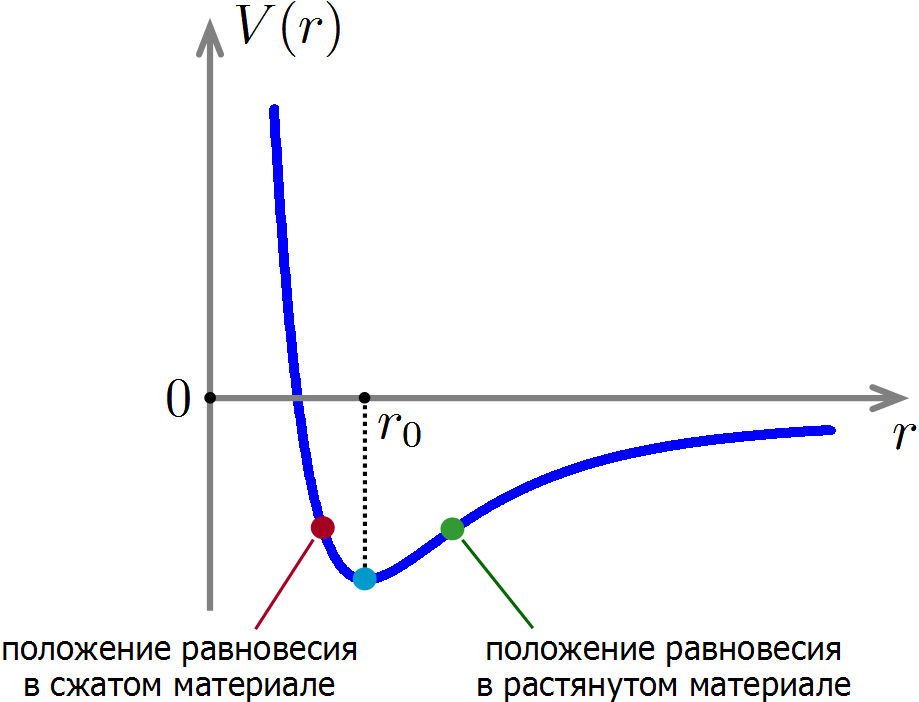
При сжатии равновесное расстояние между атомами уменьшается, а при растяжении увеличивается.
Теперь мы готовы понять, как сжатие и растяжение материала влияет на его теплоемкость. Представим, что мы сжали материал, так что расстояние между атомами при тепловом движении колеблется теперь вблизи сдвинутого влево положения равновесия. Ангармонизм при этом никуда не делся, поэтому, как и прежде, при нагреве среднее расстояние между атомами будет увеличиваться. Но при этом мы будем смещаться обратно в сторону минимума потенциальной энергии, а это значит, что энергия материала будет дополнительно уменьшаться! Так и объясняется уменьшение теплоемкости материала при сжатии: тепловое расширение приводит к небольшому дополнительному уменьшению энергии межатомных взаимодействий, поэтому на нагрев материала требуется меньше энергии.
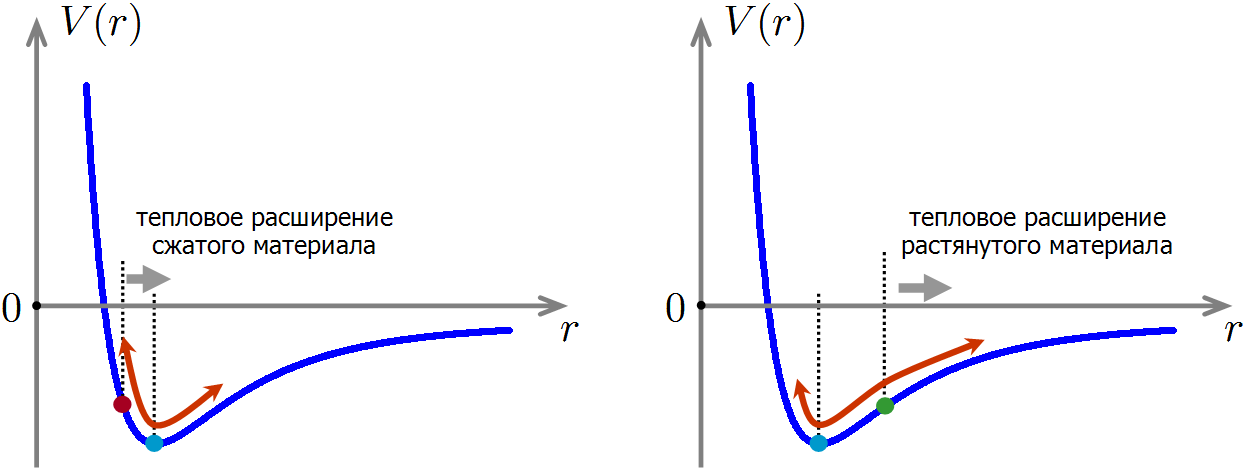
Если же материал растянут, то ситуация обратная: при тепловом расширении энергия взаимодействия атомов будет расти быстрее, чем в нерастянутом материале. Поэтому для нагрева растянутого материала на ту же температуру потребуется немного больше энергии, чем без растяжения, а значит, теплоемкость растянутого материала будет выше.
Итак, на примере олимпиадной задачи, которую многие десятилетия решали (и, может быть, продолжают решать) ошибочно, мы видим, что реальная физика иногда противоречит нашей интуиции. Поэтому так важно при решении задач аккуратно использовать математический аппарат, не ограничиваясь поверхностными рассуждениями.
По материалам статьи:
Giacomo De Palma, Mattia C. Sormani, Counterintuitive effect of gravity on the heat capacity of a solid sphere: Re-examination of a well-known problem, American Journal of Physics 83, 723 (2015).
Общедоступный препринт статьи: arxiv.org/pdf/1502.01337