Сегодня снова поворошим старое гнездо и поговорим о том, как скрыть кучку бит в картинке с котиком, посмотрим на несколько доступных инструментов и разберем самые популярные атаки. И казалось бы, при чем тут сингулярность?
Как говорится, если хочешь в чем-то разобраться, то напиши об этом статью на Хабр! (Осторожно, много текста и картинок)

Стеганография (дословно с греческого «тайнопись») — наука передачи скрываемых данных (стегосообщения) в других открытых данных (стегоконтейнеров) при сокрытии самого фак��а передачи данных. Не пугайтесь, на самом деле все не так сложно.
Итак, в каком месте изображения можно спрятать сообщение так, чтобы никто не заметил?
А мест всего два: метаданные и само изображение. Последнее совсем простое, достаточно набрать в гугле «exif». Так что начнем, пожалуй, сразу со второго.
Наиболее популярной цветовой моделью является RGB, где цвет представляется в виде трех составляющих: красного, зеленого и голубого. Каждая компонента кодируется в классическом варианте с помощью 8 бит, то есть может принимать значение от 0
до 255. Именно здесь и прячется наименее значащий бит. Важно понять, что на один RGB-цвет приходится приходится аж три таких бита.
Чтобы представить их более наглядно, проделаем пару небольших манипуляций.
Как и было обещано, возьмем картинку с котиком в png формате.

Разобьем её на три канала и в каждом канале возьмем наименее значащий бит. Создадим три новых изображения, где каждый пиксель обозначает НЗБ. Ноль — пиксель белый, единица соответственно черный.
Получаем вот что.
Но, как правило, изображение встречается в «собранном виде». Чтобы представить НЗБ трех компонент в одном изображении, достаточно компоненту в пикселе, где НЗБ равен единице, заменить на 255, и в обратном случае заменить на 0.
Представим, что все, что мы видели на последней картинке, это наше и мы в праве делать с этим все, что угодно. Тогда возьмем это как поток битов, откуда мы можем читать и куда мы можем записывать.
Берем данные, которые мы хотим вкрапить в изображение, представляем их в виде битов и последовательно записываем на место уже существующих.
Для извлечения этих данных прочитаем НЗБ как битовый поток и приведем к нужному виду. Чтобы узнать, сколько битов нужно считать, как правило, в начало записывают размер сообщения. Но это уже детали реализации.
Нужно отметить, что примерно в 50% случаев бит, который мы хотим записать, и бит в картинке будут совпадать и изменять нам ничего не придется.
Вот и все, на этом метод заканчивается.
Посмотрите на изображения ниже.
Это незаполненный стегоконтейнер:

А это заполненный на 95%:

Видите разницу? А она есть. Почему так?
Посмотрим на два цвета: (0, 0, 0) и (1, 1, 1), то есть на цвета, различные только НЗБ в каждой компоненте.
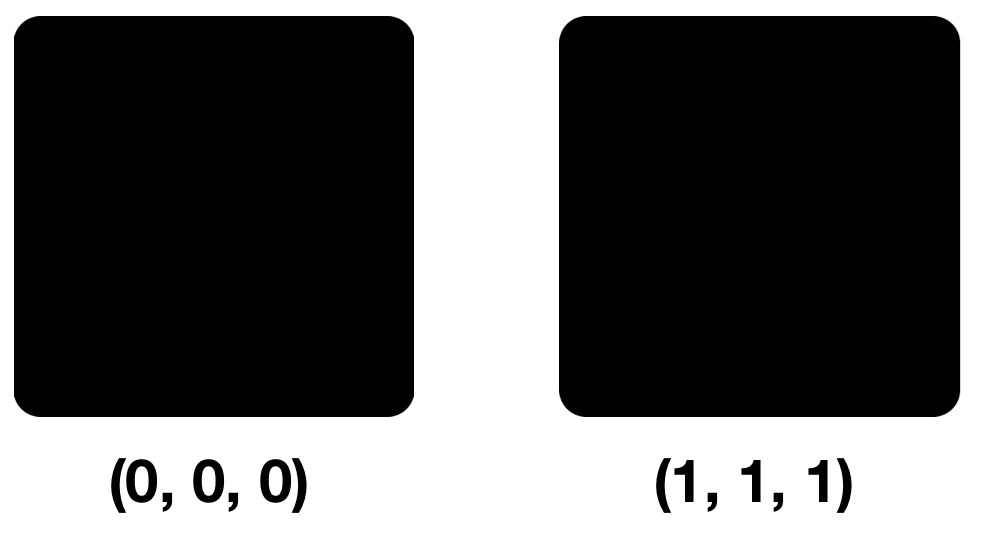
Небольшие различия в пикселях при первом, втором и третьем взгляде, заметны не будут. Дело в том, что наш глаз может различить около 10 миллионов цветов, а мозг всего лишь около 150. Модель RGB же содержит 16 777 216 цветов. Попробовать различить их все можно здесь.
Существует не так много работающих command line тулз в открытом доступе, представляющих LSB-стеганографию.
Самые популярные можно найти в таблице внизу.
И первой в списке атак на LSB-стеганографию выступает визуальная атака. Звучит странно, не правда ли? Ведь котик с секретом никак не выдавал себя как заполненный стегоконтейнер на первый взгляд. Хммм… Нужно всего лишь знать, куда смотреть. Несложно догадаться, что нашего пристального внимания заслуживают только НЗБ.
У заполненого стегоконтейнера изображение с НЗБ выглядит так:

Не верите? Вот вам НЗБ со всех трех каналов отдельно:
Это специфичный для сокрытия сообщения «рисунок» в НЗБ. На первый взгляд это кажется простым шумом. Но при рассмотрении проглядывается структура. Здесь видно, что стегоконтейнер заполнен под завязку. Если бы мы взяли сообщение в 30% от вместимости бедного котика, то получили такую бы картину:
Его НЗБ:

~70% котика осталось неизменным.
Тут стоит сделать небольшое отступление и поговорить о размерах. Что такое 30% котика? Размер котика 603х433 пикселей. 30% от этого размера равны 78459 пикселям. В каждый пиксель помещается 3 бита информации. Итого 78459 3 = 235377 бит или чуть меньше, чем 30 килобайт помещается в 30% котика. А в целого котика поместится около 100 килобайт. Такие дела.
Но мы же здесь вами не просто так. Как же все-таки обмануть глаза?
Первая мысль: засунуть сообщение в шум. Но не тут то было. Далее фрагмент заполненного стегоконтейнера и его LSB.

Прикладывая небольшое усилие, мы все-таки можем различить знакомую структуру. Не теряем надежды, господа!
Много вещей ломается статистикой, знаете ли.
Изменяя что-то в картинке, мы меняем её статистические свойства. Аналитику достаточно найти способ эти изменения зафиксировать.
Старый добрый хи-квадрат для этого начали использовать Андреас Весфилд и Андреас Пфитцманн из Университета Дрездена в своей работе «Attacks on Steganographic Systems», которую можно найти здесь.
Здесь и далее будем говорить об атаках в рамках одной цветовой плоскости, или в контексте RGB об атаках на один канал. Результаты каждой атаки можно привести к среднему и получить результат для «собранного» изображения.
Итак, атака «Хи-квадрат» основывается на том предположении, что вероятность одновременного появления соседних (отличных на наименее значащий бит) цветов (pair of values) в незаполненном стегоконтейнере крайне мала. Это действительно так, можешь поверить. Если говорить другими словами, то количество пикселей двух соседних цветов существенно отличается для пустого контейнера. Все, что нам нужно сделать, это посчитать количество пикселей каждого цвета и применить пару формул. На самом деле, это простая задачка на проверку гипотезы с использованием критерия хи-квадрат.
Немного математики?
Пусть h — массив, на i-ом месте содержащий количество пикселей i-ого цвета в исследуемом изображении.
Тогда:
Переводя это на Python получится что-то вроде этого:
Где histogram — количество пикселей цвета i в изображении,![$i \in [0, 255]$](https://habrastorage.org/getpro/habr/formulas/be3/262/f19/be3262f1907f4821fb8f9bc29e57558f.svg)
Хи-квадрат критерий для количества степеней свободы k-1 рассчитывается следующим образом (k — количество различных цветов, то есть 256):
И, наконец, P — это вероятность того, что распределения и
и  при этих условиях равны (вероятность того, что перед нами заполненый стегоконтейнер). Она рассчитывается при помощи интегрирования функции гладкости:
при этих условиях равны (вероятность того, что перед нами заполненый стегоконтейнер). Она рассчитывается при помощи интегрирования функции гладкости:
Эффективнее всего применять хи-квадрат не ко всему изображению, а только к его частям, например, к строкам. Если посчитанная вероятность для строки больше 0.5, то строку в оригинальном изображении закрасим красным. Если меньше, то зеленым. Для котика с 30% заполненностью, картина будет выглядеть следующим образом:

Весьма точно, неправда ли?
Ну вот мы и обзавелись математически обоснованной атакой, математику-то не обманешь! Или…??
Идея довольно проста: записывать биты не по порядку, а в случайные места. Для этого надо взять ГПСЧ, настроить его на выдачу одного и того же потока случайности при одном и том же сиде (aka пароле). Не зная пароля, мы не сможем настроить ГПСЧ и найти пиксели, в которых спрятано сообщение. Испытаем это на котике.
Котик (32% заполнености):

Его LSB:
Картинка выглядит шумной, но не подозрительной для неопытного аналитика. А что говорит Хи-квадрат?
Кажется, black hat победили!? Как бы не так…
Еще один статистический метод был Джессикой Фридрих, Мирославом Гольяном и Андреасом Пфитцманом в 2001 году. Он был назван как RS-метод. Оригинальную статью можно взять здесь.
Метод содержит несколько подготовительных этапов.
Изображение разделяется на группы из n пикселей. К примеру, 4 последовательных пикселя в строке. Как правило, такие группы содержат рядом стоящие пиксели.
Для нашего котика с последовательным заполнением в красном канале первыми пятью группами будут:
(Все измерения приводятся в классическом варианте RGB)
Затем мы определяем так называемую дискриминант-функцию или функцию гладкости, которая сопоставляет каждой группе пикселей действительно число. Цель это функции состоит в том, чтобы зафиксировать гладкость или «регулярность» группы пикселей G. Чем шумнее группа пикселей , тем большее значение дискриминант-функция будет иметь. Чаще всего выбирают «вариацию» группы пикселей или, проще говоря, сумму разностей соседних пикселей в группе. Но так же в ней можно учесть статистические предположения об изображении.
, тем большее значение дискриминант-функция будет иметь. Чаще всего выбирают «вариацию» группы пикселей или, проще говоря, сумму разностей соседних пикселей в группе. Но так же в ней можно учесть статистические предположения об изображении.
Значения функции гладкости для группы пикселей из нашего примера:
Далее определяется класс функций флиппинга от одного пикселя.
Они должны обладать некоторыми свойствами.
Где — любая функция из одного класса,
— любая функция из одного класса,  — прямая функция флиппинга, а
— прямая функция флиппинга, а  — обратная. В дополнение обычно обозначается тождественная функция флиппинга
— обратная. В дополнение обычно обозначается тождественная функция флиппинга  , которая не меняет пиксель.
, которая не меняет пиксель.
Функции флиппинга на python могут выглядеть примерно вот так:
К каждой группе пикселей мы применяем одну из функций флиппинга и на основании значения функции-дескриминанта до и после флиппинга, мы определяем тип группы пикселей: обычный (Regular), единичный/необычный (Singular), ибесполезный непригодный (unusable). Так как последний тип в дальнейшем не используется, метод был назван по первым буквам ключевых типов. Вот и весь секрет названия, сингулярность здесь ни при чем :)
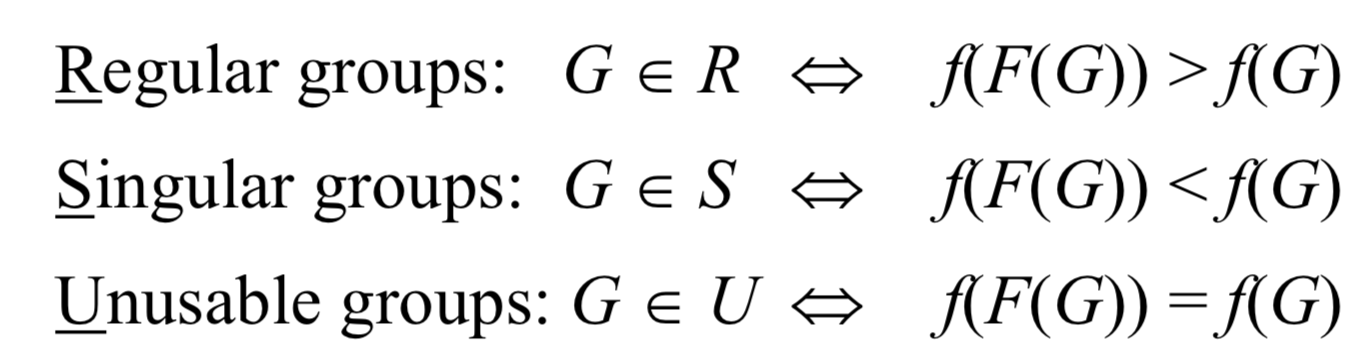
Мы можемзахотеть применить разный флиппинг к разным пикселям, для этого определяют маску М с n значениями -1, 0 или 1.
Пусть маска для нашего примера будет классическая — [1, 0, 0, 1]. Опытным путем было обнаружено, что лучше всего для этого метода подходят симметричные маски, не содержащие . Также удачными вариантами будут: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Применим флиппинг для групп из примера, подсчитаем значение гладкости и определим тип группы пикселей:
. Также удачными вариантами будут: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Применим флиппинг для групп из примера, подсчитаем значение гладкости и определим тип группы пикселей:
Обозначим число регулярных групп для маски M как (в процентных долях всех групп), и
(в процентных долях всех групп), и  для сингулярных групп.
для сингулярных групп.
Тогда и
и  , для отрицательной маски (все компоненты маски умножены на -1), т.к.
, для отрицательной маски (все компоненты маски умножены на -1), т.к.  , при этом
, при этом  может быть пустой. Аналогично для отрицательной маски.
может быть пустой. Аналогично для отрицательной маски.
Основная статистическая гипотеза состоит в том, что в типичном изображении ожидаемое значение равно значению
равно значению  , и то же самое верно для
, и то же самое верно для  и
и  . Это доказывают экспериментальные данные и некоторые танцы с бубном вокруг последнего свойства функции флиппинга.
. Это доказывают экспериментальные данные и некоторые танцы с бубном вокруг последнего свойства функции флиппинга.
Проверим это на нашем маленьком примере? Учитывая небольшой размер выборки, мы можем не подтвердить данную гипотезу. Посмотрим, что же будет с инвертированной маской: [-1, 0, 0, -1].
Ну тут все очевидно.
Однако разность между и
и  стремиться к нулю по мере увеличения длины m встроенного сообщения и мы получаем, что
стремиться к нулю по мере увеличения длины m встроенного сообщения и мы получаем, что  .
.
Забавно, что рандомизация плоскости LSB оказывает противоположное влияние на и
и  . Их разность увеличивается с длиной m встроенного сообщения. Объяснение этому явлению можно найти в оригинальной статье.
. Их разность увеличивается с длиной m встроенного сообщения. Объяснение этому явлению можно найти в оригинальной статье.
Вот график ,
,  ,
,  и
и  в зависимости от количества пикселей с инвертированными LSB, его называют RS-диаграммой. Ось x представляет собой процент пикселей с инвертированными LSB, ось y — относительное число регулярных и сингулярных групп с масками M и -M,
в зависимости от количества пикселей с инвертированными LSB, его называют RS-диаграммой. Ось x представляет собой процент пикселей с инвертированными LSB, ось y — относительное число регулярных и сингулярных групп с масками M и -M, ![$M=[0~1~ 1 ~0]$](https://habrastorage.org/getpro/habr/formulas/f65/77d/734/f6577d734f22f11d74a9dbc677e4b34f.svg) .
.
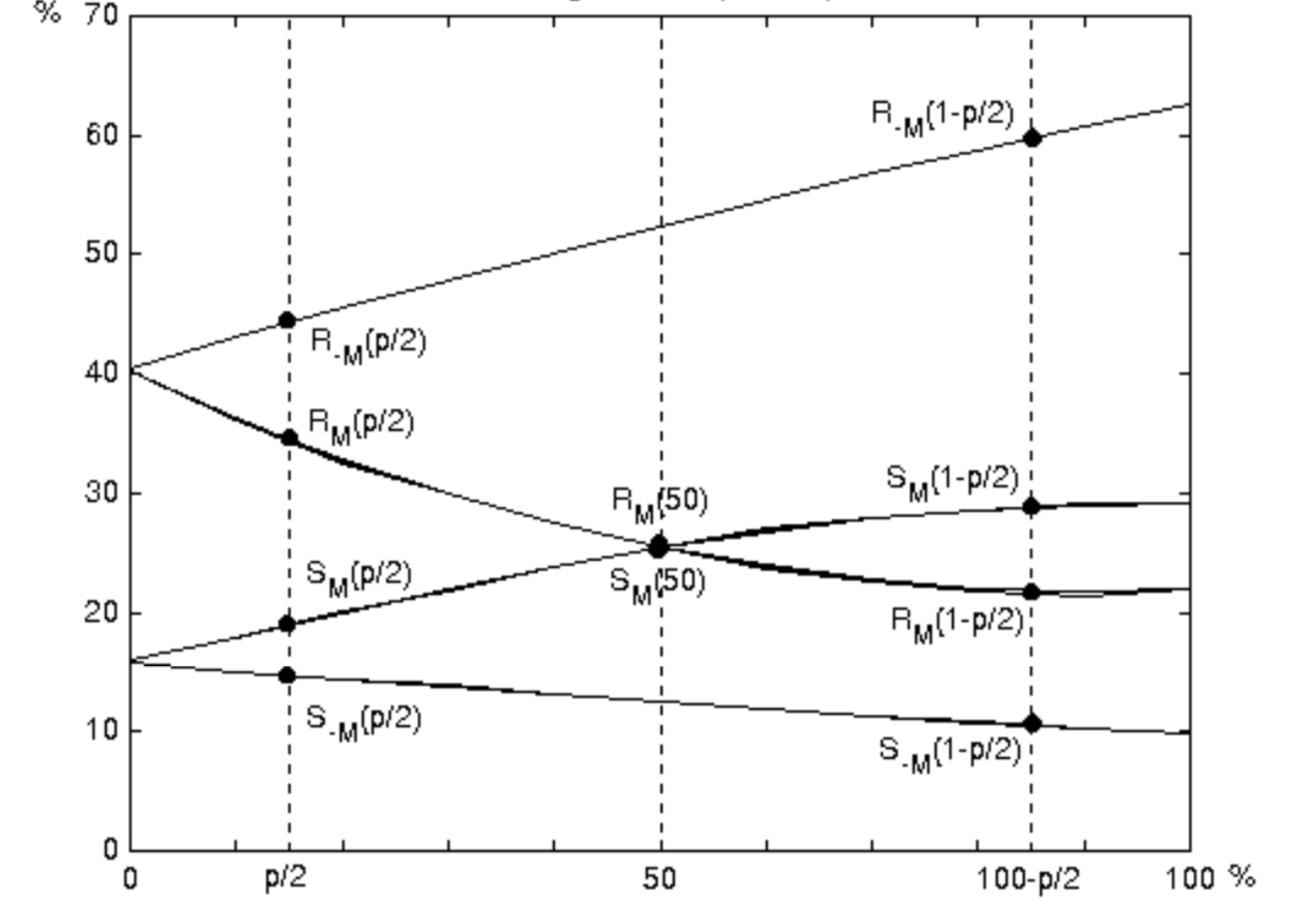
Суть метода RS-стегоанализа заключается в оценке четырех кривых диаграммы RS и вычислении их пересечения с использованием экстраполяции. Предположим, что у нас есть стегоконтейнер с сообщением неизвестной длины p (в процентах от пикселей), встроенное в младшие разряды случайно выбранных пикселей (то есть с использованием RandomLSB). Наши начальные измерения числа групп R и S соответствуют точкам ,
,  ,
,  и
и  . Мы берем точки именно от половины длины сообщения, так как сообщение является случайным битовым потоком и в среднем, как было сказано ранее, только одна половина пикселей будет изменена посредством внедрения сообщения.
. Мы берем точки именно от половины длины сообщения, так как сообщение является случайным битовым потоком и в среднем, как было сказано ранее, только одна половина пикселей будет изменена посредством внедрения сообщения.
Если мы инвертируем LSB всех пикселей на изображении и вычислим количество R и S групп, мы получим четыре точки ,
,  ,
,  и
и  . Поскольку эти две точки зависят от конкретной рандомизации LSB, мы должны многократно повторять этот процесс и оценивать
. Поскольку эти две точки зависят от конкретной рандомизации LSB, мы должны многократно повторять этот процесс и оценивать  и
и  из статистических выборок.
из статистических выборок.
Мы можем условно провести прямые через точки ,
,  и
и  ,
,  .
.
Точки ,
,  ,
,  и
и  ,
,  ,
,  определяют две параболы. Каждая парабола и соответствующая линия пересекаются слева. Среднее арифметическое x-координат обоих пересечений позволяет оценить неизвестную длину сообщения p.
определяют две параболы. Каждая парабола и соответствующая линия пересекаются слева. Среднее арифметическое x-координат обоих пересечений позволяет оценить неизвестную длину сообщения p.
Чтобы избежать долгой статистической оценки средних точек RM(1/2) и SM(1/2), можно принять еще пару соображений:
Эти два предположения позволяют получить простую формулу для длины секретного сообщения p. После масштабирования оси x, так что p / 2 становится 0, а 1 — p / 2 становится равным 1, x-координата точки пересечения является корнем из следующего квадратного уравнения
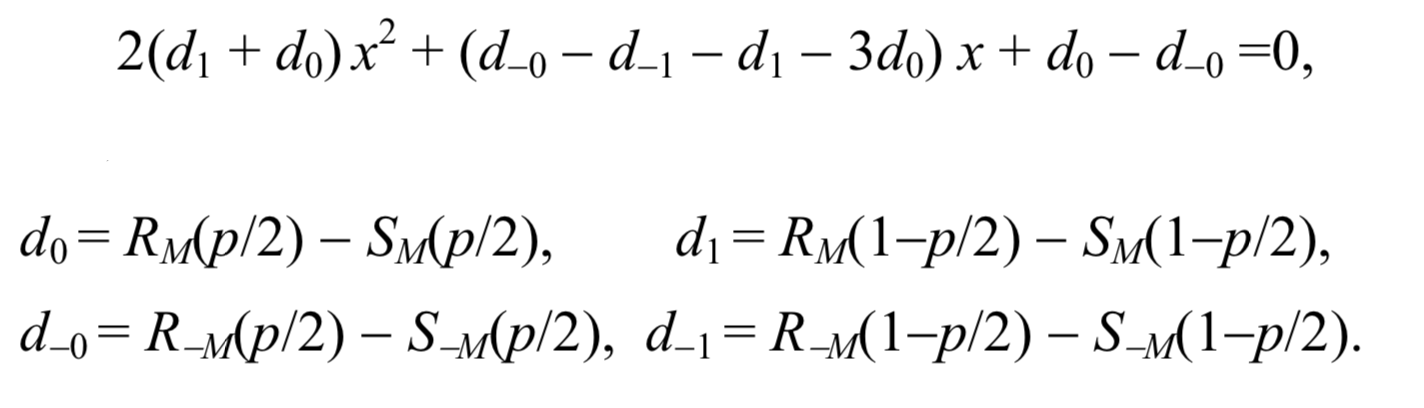
Тогда длину сообщения можно вычислить по формуле:
Тут на сцену выходит наш котик. (Не пора ли дать ему имя?)
Итак, у нас имеется:
(Если у вас очень много свободного времени, то можете подсчитать их самостоятельно, а пока предлагаю поверить мои подсчетам)
На повестке дня у нас осталась одна голая математика. Все же помнят, как решать квадратные уравнения?
Подставив все d в формулу выше, получим квадратное уравнение, которое решим, как учили в школе.
Возьмем меньший по модулю корень, то есть . Тогда примерная оценка для встроенного в котика сообщения будет такая:
. Тогда примерная оценка для встроенного в котика сообщения будет такая:
Да, у этого метода есть один большой плюс и один большой минус. Плюс заключается в том, что метод работает как с обычной LSB-стеганографией, так и RandomLSB-стеганографией. Хи-квадрат такой возможностью похвастаться не может. Нашего рандомного котика метод распознал точно и дал оценку длине сообщения в 0.3256, что очень-очень точно.
Минус же кроется в большой (очень большой) погрешности данного метода, растущей вместе с длинной сообщения при последовательном встраивании. К примеру, для котика с заполненностью в 30% моя реализация метода дает примерную среднюю оценку на три канала в 0.4633 или в 46% от общей вместимости, при заполненности более 95% — 0.8597. Зато для пустого котика аж 0.0054. И это общая тенденция, не зависящая от реализации. Наиболее точные результаты при обычном LSB метод дает при длине встраиваемого сообщение в 10%+-5%.
Чтобы не попасться, надо быть неожиданным и использовать ±1 кодирование. Вместо того чтобы изменять наименьший значащий бит в байте цвета, мы будем весь байт либо увеличивать, либо уменьшать на единицу. Есть только два исключения:
Для всех других значений байта мы совершенно случайно выбираем либо увеличение на единицу, либо уменьшение. Поверх данной манипуляции LSB будет изменяться так, как менялся раньше. Для пущей надежности лучше брать случайные байты для записи сообщения.
Вот наш друг котик:

Внешне внедрение незаметно ровно по той же причине, почему не было видны разницы между (0, 0, 0) и (1, 1, 1).
Срез LSB остается просто шумным из-за записи в случайные места.

Хи-квадрат по-прежнему слеп, а RS-метод дает приблизительную оценку 0.0036.
Чтобы не очень сильно радоваться, прочтите вот эту статью.
У самых внимательных может возникнуть вопрос, как же мы можем достать сообщение, если целые байты изменяются случайно, а пароля для настаивания ГПСЧ у нас нет (лучше использовать разные сиды aka состояния генератора aka пароли для работы с RandomLSB и ±1 кодированием). Ответ максимально прост. Мы достаем сообщение так же, как это делали и без ±1 кодирования. Мы вообще можем не знать о его использовании. Повторюсь, данную уловку мы используем только для обхода автоматических средств детектирования. При внедрении/извлечении сообщения мы работаем только с его LSB и ничем более. Однако при детектировании нам необходимо брать во внимание контекст внедрения, то есть все байты изображения, чтобы построить статистические оценки. Именно в этом и заключается весь успех ±1 кодирования.
Еще одна весьма неплохая попытка использовать статистику против LSB-стеганографии была предпринята в методе под названием Sample Pairs. Найти его можно здесь. Его присутствие здесь сделало бы статью слишком академичной, поэтому заинтересованным оставляю это для внеклассного чтения. Но предвосхищая вопросы аудитории, отвечу сразу: нет, он не ловит ±1 кодирование.
И конечно машинное обучение. Современные методы на основе ML дают очень хорошие результаты. Об этом можно почитать тут и тут.
По мотивам этой статьи была написана (пока) небольшая тулза. Она может генерировать данные, осуществлять визуальную атаку раздельно по каналам, подсчитывать RS-, SPA-оценку и визуализировать результаты Хи-квадрат. И она не собирается на этом останавливаться.
Подводя черту, хочется дать пару советов:
Буду рада увидеть ваши предложения, дополнения, исправления и другой feedback!
P.S. Хочу выразить особую благодарность PavelMSTU за консультации и мотивационные пинки.
Как говорится, если хочешь в чем-то разобраться, то напиши об этом статью на Хабр! (Осторожно, много текста и картинок)

Стеганография (дословно с греческого «тайнопись») — наука передачи скрываемых данных (стегосообщения) в других открытых данных (стегоконтейнеров) при сокрытии самого фак��а передачи данных. Не пугайтесь, на самом деле все не так сложно.
Итак, в каком месте изображения можно спрятать сообщение так, чтобы никто не заметил?
А мест всего два: метаданные и само изображение. Последнее совсем простое, достаточно набрать в гугле «exif». Так что начнем, пожалуй, сразу со второго.
Least Significant Bit
Наиболее популярной цветовой моделью является RGB, где цвет представляется в виде трех составляющих: красного, зеленого и голубого. Каждая компонента кодируется в классическом варианте с помощью 8 бит, то есть может принимать значение от 0
до 255. Именно здесь и прячется наименее значащий бит. Важно понять, что на один RGB-цвет приходится приходится аж три таких бита.
Чтобы представить их более наглядно, проделаем пару небольших манипуляций.
Как и было обещано, возьмем картинку с котиком в png формате.

Разобьем её на три канала и в каждом канале возьмем наименее значащий бит. Создадим три новых изображения, где каждый пиксель обозначает НЗБ. Ноль — пиксель белый, единица соответственно черный.
Получаем вот что.
Красный канал 

Зеленый канал 

Синий канал 
Но, как правило, изображение встречается в «собранном виде». Чтобы представить НЗБ трех компонент в одном изображении, достаточно компоненту в пикселе, где НЗБ равен единице, заменить на 255, и в обратном случае заменить на 0.
Тогда получается вот это 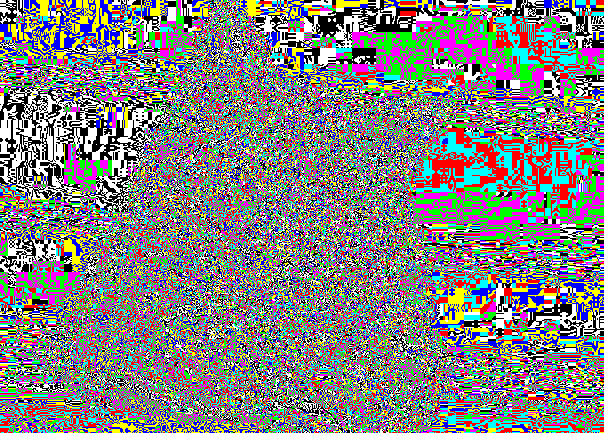
Может засунем сюда что-нибудь?
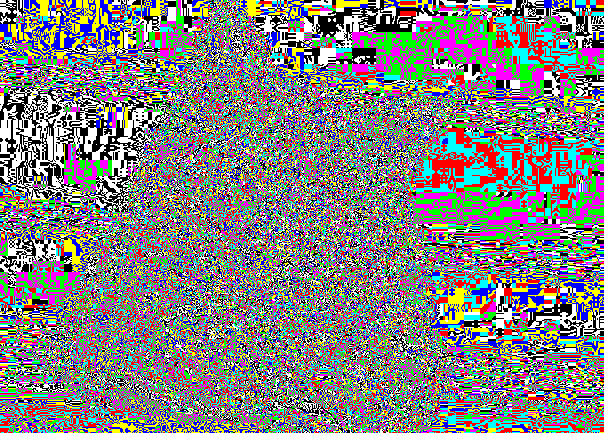
Может засунем сюда что-нибудь?
Но не менее значимый
Представим, что все, что мы видели на последней картинке, это наше и мы в праве делать с этим все, что угодно. Тогда возьмем это как поток битов, откуда мы можем читать и куда мы можем записывать.
Берем данные, которые мы хотим вкрапить в изображение, представляем их в виде битов и последовательно записываем на место уже существующих.
Для извлечения этих данных прочитаем НЗБ как битовый поток и приведем к нужному виду. Чтобы узнать, сколько битов нужно считать, как правило, в начало записывают размер сообщения. Но это уже детали реализации.
Нужно отметить, что примерно в 50% случаев бит, который мы хотим записать, и бит в картинке будут совпадать и изменять нам ничего не придется.
Вот и все, на этом метод заканчивается.
Почему это работает?
Посмотрите на изображения ниже.
Это незаполненный стегоконтейнер:

А это заполненный на 95%:

Видите разницу? А она есть. Почему так?
Посмотрим на два цвета: (0, 0, 0) и (1, 1, 1), то есть на цвета, различные только НЗБ в каждой компоненте.

Небольшие различия в пикселях при первом, втором и третьем взгляде, заметны не будут. Дело в том, что наш глаз может различить около 10 миллионов цветов, а мозг всего лишь около 150. Модель RGB же содержит 16 777 216 цветов. Попробовать различить их все можно здесь.
Из командной строки
Существует не так много работающих command line тулз в открытом доступе, представляющих LSB-стеганографию.
Самые популярные можно найти в таблице внизу.
| Тулза | Типы файлов | Описание | Сокрытие | Извлечение |
| openstego | PNG | Может использоваться не только для сокрытия данных, но и для водяных знаков. Использует RandomLSB — улучшенный алгоритм LSB с записью в Random Least Significant Bit. Поддерживает шифрование. Имеет также GUI. |
openstego embed -mf secret.txt -cf cover.png -p password -sf stego.png |
openstego extract -sf openstego.png -p abcd -xf output.txt |
| stegano | PNG | Работает не только с классическим LSB. Имеет гибкую настройку. Может использоваться как модуль Python. Самая привлекательная (как по мне). |
stegano-lsb hide --input cover.jpg -f secret.txt -e UTF-8 --output stego.png |
stegano-lsb reveal -i stego.png -e UTF-8 -o output.txt |
| cloackedpixel | PNG, JPG | Простенькая тулза. Плохо справляется с большим сообщением. (Точнее вообще никак) Поддерживает шифрование. |
cloackedpixel hide cover.jpg secret.txt password |
cloackedpixel extract cover.jpg-stego.png output.txt password |
| LSBSteg | PNG, BMP | Небольшая программа на Python c читабельным кодом. |
LSBSteg encode -i cover.png -o stego.png -f secret.txt |
LSBSteg decode -i stego.png -o output.txt |
А где котик?
И первой в списке атак на LSB-стеганографию выступает визуальная атака. Звучит странно, не правда ли? Ведь котик с секретом никак не выдавал себя как заполненный стегоконтейнер на первый взгляд. Хммм… Нужно всего лишь знать, куда смотреть. Несложно догадаться, что нашего пристального внимания заслуживают только НЗБ.
У заполненого стегоконтейнера изображение с НЗБ выглядит так:

Не верите? Вот вам НЗБ со всех трех каналов отдельно:
Красный канал 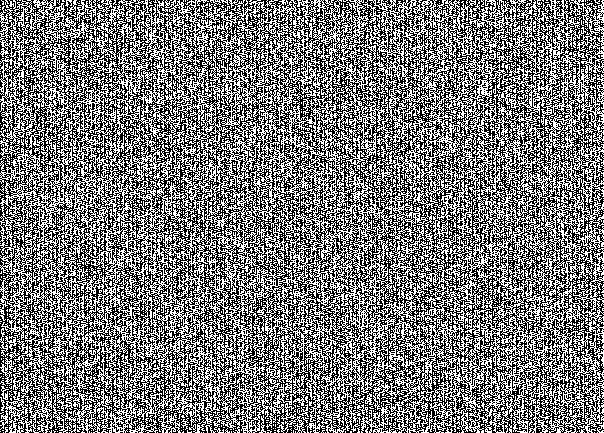
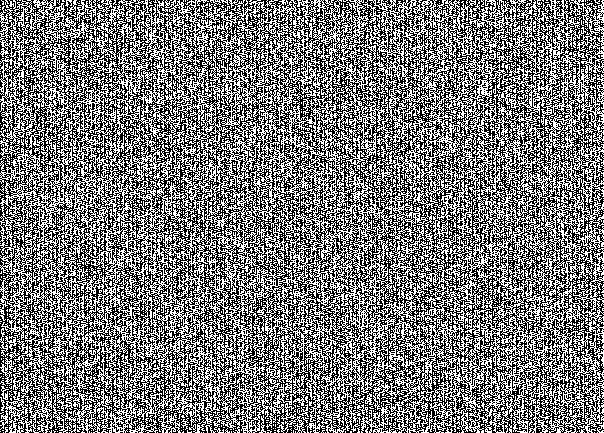
Зеленый канал 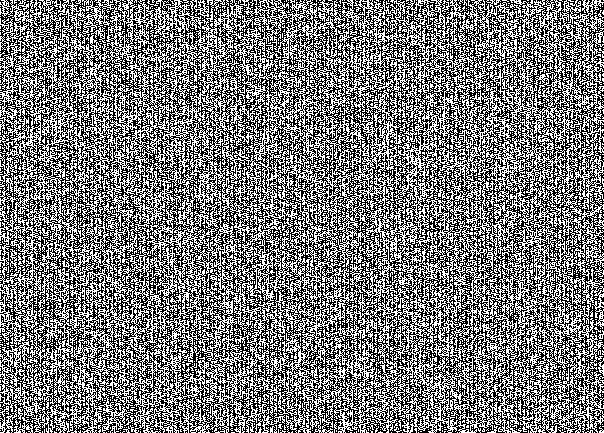
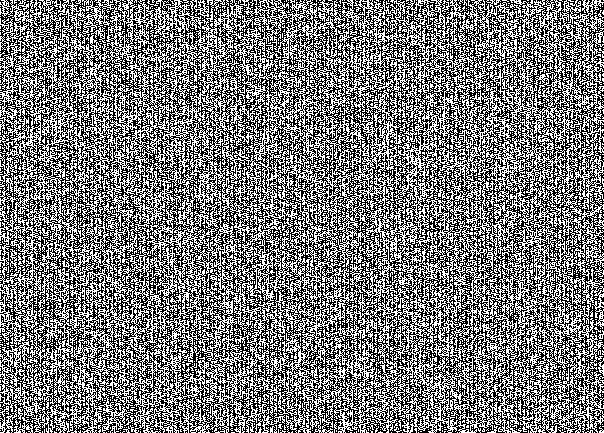
Синий канал 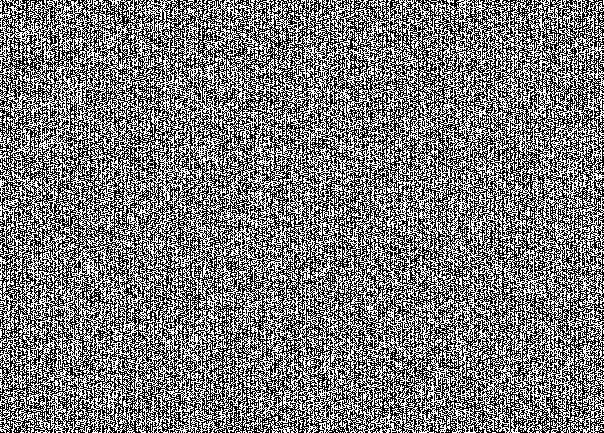
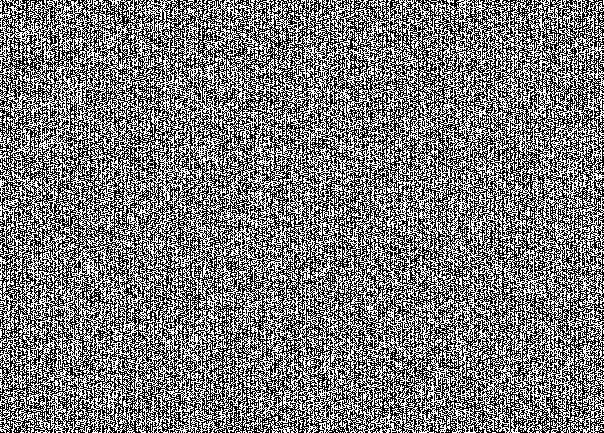
Это специфичный для сокрытия сообщения «рисунок» в НЗБ. На первый взгляд это кажется простым шумом. Но при рассмотрении проглядывается структура. Здесь видно, что стегоконтейнер заполнен под завязку. Если бы мы взяли сообщение в 30% от вместимости бедного котика, то получили такую бы картину:
Контейнер 

Его НЗБ:

~70% котика осталось неизменным.
Тут стоит сделать небольшое отступление и поговорить о размерах. Что такое 30% котика? Размер котика 603х433 пикселей. 30% от этого размера равны 78459 пикселям. В каждый пиксель помещается 3 бита информации. Итого 78459 3 = 235377 бит или чуть меньше, чем 30 килобайт помещается в 30% котика. А в целого котика поместится около 100 килобайт. Такие дела.
Но мы же здесь вами не просто так. Как же все-таки обмануть глаза?
Первая мысль: засунуть сообщение в шум. Но не тут то было. Далее фрагмент заполненного стегоконтейнера и его LSB.

Прикладывая небольшое усилие, мы все-таки можем различить знакомую структуру. Не теряем надежды, господа!
Хи-хи-хи
Много вещей ломается статистикой, знаете ли.
Изменяя что-то в картинке, мы меняем её статистические свойства. Аналитику достаточно найти способ эти изменения зафиксировать.
Старый добрый хи-квадрат для этого начали использовать Андреас Весфилд и Андреас Пфитцманн из Университета Дрездена в своей работе «Attacks on Steganographic Systems», которую можно найти здесь.
Здесь и далее будем говорить об атаках в рамках одной цветовой плоскости, или в контексте RGB об атаках на один канал. Результаты каждой атаки можно привести к среднему и получить результат для «собранного» изображения.
Итак, атака «Хи-квадрат» основывается на том предположении, что вероятность одновременного появления соседних (отличных на наименее значащий бит) цветов (pair of values) в незаполненном стегоконтейнере крайне мала. Это действительно так, можешь поверить. Если говорить другими словами, то количество пикселей двух соседних цветов существенно отличается для пустого контейнера. Все, что нам нужно сделать, это посчитать количество пикселей каждого цвета и применить пару формул. На самом деле, это простая задачка на проверку гипотезы с использованием критерия хи-квадрат.
Немного математики?
Пусть h — массив, на i-ом месте содержащий количество пикселей i-ого цвета в исследуемом изображении.
Тогда:
- Измеренная частота появления цвета
:
- Теоретически ожидаемая частота появления цвета
:
UPD: Небольшое пояснение к формулам выше
У многих возникнет вопрос: почему мы берем такой индекс? Почему именно 2k?
Нужно держать в голове, что мы работаем с соседними цветами, то есть с цветами (числами), различающимися только наименее значащим битом. Они идут парами последовательно:
Если количество пикселей цвета 2k и 2k+1 будет сильно различаться, то различаться будут измеренная частота и теоретически ожидаемая, что нормально для незаполненного стегоконтейнера.
Нужно держать в голове, что мы работаем с соседними цветами, то есть с цветами (числами), различающимися только наименее значащим битом. Они идут парами последовательно:
Если количество пикселей цвета 2k и 2k+1 будет сильно различаться, то различаться будут измеренная частота и теоретически ожидаемая, что нормально для незаполненного стегоконтейнера.
Переводя это на Python получится что-то вроде этого:
for k in range(0, len(histogram) // 2):
expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2))
observed.append(histogram[2 * k])
Где histogram — количество пикселей цвета i в изображении,
Хи-квадрат критерий для количества степеней свободы k-1 рассчитывается следующим образом (k — количество различных цветов, то есть 256):
И, наконец, P — это вероятность того, что распределения
Эффективнее всего применять хи-квадрат не ко всему изображению, а только к его частям, например, к строкам. Если посчитанная вероятность для строки больше 0.5, то строку в оригинальном изображении закрасим красным. Если меньше, то зеленым. Для котика с 30% заполненностью, картина будет выглядеть следующим образом:

Весьма точно, неправда ли?
Ну вот мы и обзавелись математически обоснованной атакой, математику-то не обманешь! Или…??
Shuffle Dance
Идея довольно проста: записывать биты не по порядку, а в случайные места. Для этого надо взять ГПСЧ, настроить его на выдачу одного и того же потока случайности при одном и том же сиде (aka пароле). Не зная пароля, мы не сможем настроить ГПСЧ и найти пиксели, в которых спрятано сообщение. Испытаем это на котике.
Котик (32% заполнености):

Его LSB:
Картинка выглядит шумной, но не подозрительной для неопытного аналитика. А что говорит Хи-квадрат?
А что говорит Хи-квадрат? 

Кажется, black hat победили!? Как бы не так…
Регулярность-сингулярность
Еще один статистический метод был Джессикой Фридрих, Мирославом Гольяном и Андреасом Пфитцманом в 2001 году. Он был назван как RS-метод. Оригинальную статью можно взять здесь.
Метод содержит несколько подготовительных этапов.
Изображение разделяется на группы из n пикселей. К примеру, 4 последовательных пикселя в строке. Как правило, такие группы содержат рядом стоящие пиксели.
Для нашего котика с последовательным заполнением в красном канале первыми пятью группами будут:
- [78, 78, 79, 78]
- [78, 78, 78, 78]
- [78, 79, 78, 79]
- [79, 76, 79, 76]
- [76, 76, 76, 77]
(Все измерения приводятся в классическом варианте RGB)
Затем мы определяем так называемую дискриминант-функцию или функцию гладкости, которая сопоставляет каждой группе пикселей действительно число. Цель это функции состоит в том, чтобы зафиксировать гладкость или «регулярность» группы пикселей G. Чем шумнее группа пикселей
Значения функции гладкости для группы пикселей из нашего примера:
- f(78, 78, 79, 78) = 2
- f(78, 78, 78, 78) = 0
- f(78, 79, 78, 79) = 3
- f(79, 76, 79, 76) = 9
- f(76, 76, 76, 77) = 1
Далее определяется класс функций флиппинга от одного пикселя.
Они должны обладать некоторыми свойствами.
Где
Функции флиппинга на python могут выглядеть примерно вот так:
def flip(val):
if val & 1:
return val - 1
return val + 1
def invert_flip(val):
if val & 1:
return val + 1
return val - 1
def null_flip(val):
return val
К каждой группе пикселей мы применяем одну из функций флиппинга и на основании значения функции-дескриминанта до и после флиппинга, мы определяем тип группы пикселей: обычный (Regular), единичный/необычный (Singular), и
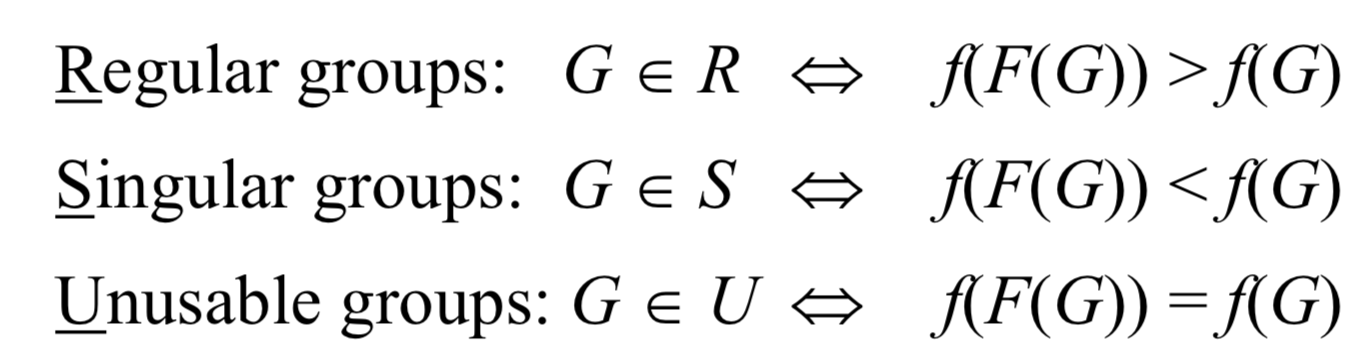
Мы можем
Пусть маска для нашего примера будет классическая — [1, 0, 0, 1]. Опытным путем было обнаружено, что лучше всего для этого метода подходят симметричные маски, не содержащие
(78, 78, 79, 78) = [79, 78, 79, 79];
f(79, 78, 79, 79) = 2 = 2 = f(78, 78, 79, 78)
Unusable группа
(78, 78, 78, 78) = [79, 78, 78, 79];
f(79, 78, 78, 79) = 2 > 0 = f(78, 78, 78, 78)
Regular группа
(78, 79, 78, 79) = [79, 79, 78, 78];
f(79, 79, 78, 78) = 1 < 3=f(78, 79, 78, 79) Singular группа
(79, 76, 79, 76) = [78, 76, 79, 77];
f(78, 76, 79, 77) = 7 < 9=f(79, 76, 79, 76) Singular группа
(76, 76, 76, 77) = [77, 76, 76, 76];
f(77, 76, 76, 76) = 1 = 1 = f(76, 76, 76, 77)
Unusable группа
Обозначим число регулярных групп для маски M как
Тогда
Основная статистическая гипотеза состоит в том, что в типичном изображении ожидаемое значение
Проверим это на нашем маленьком примере? Учитывая небольшой размер выборки, мы можем не подтвердить данную гипотезу. Посмотрим, что же будет с инвертированной маской: [-1, 0, 0, -1].
- F_M(78, 78, 79, 78) = [77, 78, 79, 77];
f(77, 78, 79, 77) = 4 > 2 = f(77, 78, 79, 77)
Regular группа
- F_M(78, 78, 78, 78) = [77, 78, 78, 77];
f(77, 78, 78, 77) = 2 > 0 = f(78, 78, 78, 78)
Regular группа
- F_M(78, 79, 78, 79) = [77, 79, 78, 80];
f(77, 79, 78, 80) = 5 > 3 = f(78, 79, 78, 79)
Regular группа
- F_M(79, 76, 79, 76) = [80, 76, 79, 75];
f(80, 76, 79, 75) = 11 > 9 = f(79, 76, 79, 76)
Regular группа
- F_M(76, 76, 76, 77) = [75, 76, 76, 78];
f(75, 76, 76, 78) = 3 > 1 = f(76, 76, 76, 77)
Regular группа
Ну тут все очевидно.
Однако разность между
Забавно, что рандомизация плоскости LSB оказывает противоположное влияние на
Вот график

Суть метода RS-стегоанализа заключается в оценке четырех кривых диаграммы RS и вычислении их пересечения с использованием экстраполяции. Предположим, что у нас есть стегоконтейнер с сообщением неизвестной длины p (в процентах от пикселей), встроенное в младшие разряды случайно выбранных пикселей (то есть с использованием RandomLSB). Наши начальные измерения числа групп R и S соответствуют точкам
Если мы инвертируем LSB всех пикселей на изображении и вычислим количество R и S групп, мы получим четыре точки
Мы можем условно провести прямые через точки
Точки
Чтобы избежать долгой статистической оценки средних точек RM(1/2) и SM(1/2), можно принять еще пару соображений:
- Точка пересечения кривых
и
имеет ту же координату x, что и точка пересечения для кривых
и
. Это по существу более строгая версия нашей статистической гипотезы. (см. выше)
- Кривые RM и SM пересекаются при m = 50%, или
.
Эти два предположения позволяют получить простую формулу для длины секретного сообщения p. После масштабирования оси x, так что p / 2 становится 0, а 1 — p / 2 становится равным 1, x-координата точки пересечения является корнем из следующего квадратного уравнения
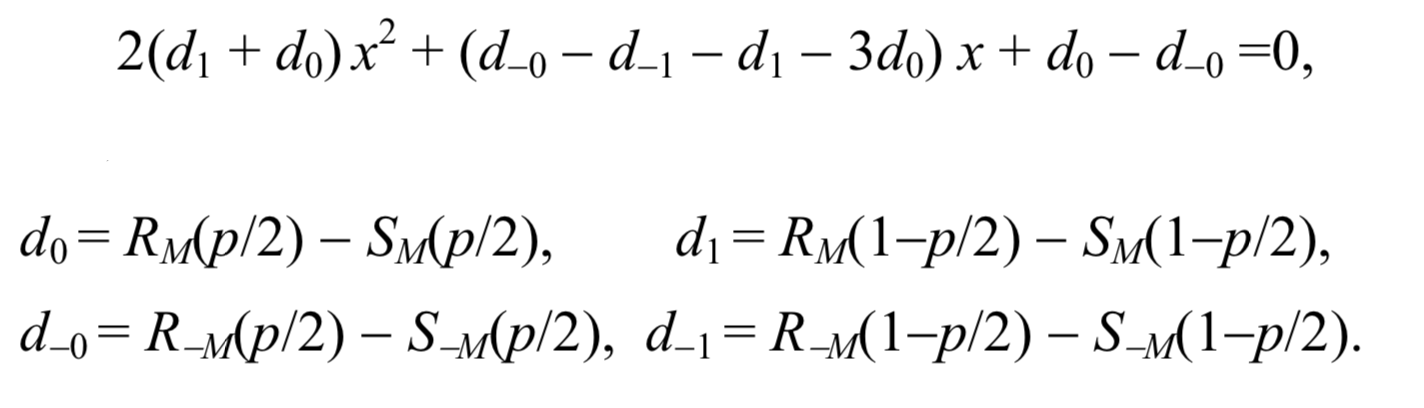
Тогда длину сообщения можно вычислить по формуле:
Тут на сцену выходит наш котик. (Не пора ли дать ему имя?)
Итак, у нас имеется:
- Regular групп RM(p/2): 23121 шт.
- Singular групп SM(p/2): 14124 шт.
- Regular групп с инвертированной маской R-M(p/2): 37191 шт.
- Singular групп с инвертированной маской S-M(p/2): 8440 шт.
- Regular групп с инвертированными LSB RM(1-p/2): 20298 шт.
- Singular групп с инвертированными LSB SM(1-p/2): 16206 шт.
- Regular групп с инвертированными LSB и с инвертированной маской R-M(1-p/2): 40603 шт.
- Singular групп с инвертированными LSB и с инвертированной маской S-M(1-p/2): 6947 шт.
(Если у вас очень много свободного времени, то можете подсчитать их самостоятельно, а пока предлагаю поверить мои подсчетам)
На повестке дня у нас осталась одна голая математика. Все же помнят, как решать квадратные уравнения?
Подставив все d в формулу выше, получим квадратное уравнение, которое решим, как учили в школе.
Возьмем меньший по модулю корень, то есть
Да, у этого метода есть один большой плюс и один большой минус. Плюс заключается в том, что метод работает как с обычной LSB-стеганографией, так и RandomLSB-стеганографией. Хи-квадрат такой возможностью похвастаться не может. Нашего рандомного котика метод распознал точно и дал оценку длине сообщения в 0.3256, что очень-очень точно.
Минус же кроется в большой (очень большой) погрешности данного метода, растущей вместе с длинной сообщения при последовательном встраивании. К примеру, для котика с заполненностью в 30% моя реализация метода дает примерную среднюю оценку на три канала в 0.4633 или в 46% от общей вместимости, при заполненности более 95% — 0.8597. Зато для пустого котика аж 0.0054. И это общая тенденция, не зависящая от реализации. Наиболее точные результаты при обычном LSB метод дает при длине встраиваемого сообщение в 10%+-5%.
Плюс-минус
Чтобы не попасться, надо быть неожиданным и использовать ±1 кодирование. Вместо того чтобы изменять наименьший значащий бит в байте цвета, мы будем весь байт либо увеличивать, либо уменьшать на единицу. Есть только два исключения:
- мы не можем уменьшить ноль, поэтому мы будем его увеличивать,
- мы также не можем увеличить 255, так что это значение мы всегда будем уменьшать.
Для всех других значений байта мы совершенно случайно выбираем либо увеличение на единицу, либо уменьшение. Поверх данной манипуляции LSB будет изменяться так, как менялся раньше. Для пущей надежности лучше брать случайные байты для записи сообщения.
Вот наш друг котик:

Внешне внедрение незаметно ровно по той же причине, почему не было видны разницы между (0, 0, 0) и (1, 1, 1).
Срез LSB остается просто шумным из-за записи в случайные места.

Хи-квадрат по-прежнему слеп, а RS-метод дает приблизительную оценку 0.0036.
Чтобы не очень сильно радоваться, прочтите вот эту статью.
У самых внимательных может возникнуть вопрос, как же мы можем достать сообщение, если целые байты изменяются случайно, а пароля для настаивания ГПСЧ у нас нет (лучше использовать разные сиды aka состояния генератора aka пароли для работы с RandomLSB и ±1 кодированием). Ответ максимально прост. Мы достаем сообщение так же, как это делали и без ±1 кодирования. Мы вообще можем не знать о его использовании. Повторюсь, данную уловку мы используем только для обхода автоматических средств детектирования. При внедрении/извлечении сообщения мы работаем только с его LSB и ничем более. Однако при детектировании нам необходимо брать во внимание контекст внедрения, то есть все байты изображения, чтобы построить статистические оценки. Именно в этом и заключается весь успех ±1 кодирования.
Вместо заключения
Еще одна весьма неплохая попытка использовать статистику против LSB-стеганографии была предпринята в методе под названием Sample Pairs. Найти его можно здесь. Его присутствие здесь сделало бы статью слишком академичной, поэтому заинтересованным оставляю это для внеклассного чтения. Но предвосхищая вопросы аудитории, отвечу сразу: нет, он не ловит ±1 кодирование.
И конечно машинное обучение. Современные методы на основе ML дают очень хорошие результаты. Об этом можно почитать тут и тут.
По мотивам этой статьи была написана (пока) небольшая тулза. Она может генерировать данные, осуществлять визуальную атаку раздельно по каналам, подсчитывать RS-, SPA-оценку и визуализировать результаты Хи-квадрат. И она не собирается на этом останавливаться.
Подводя черту, хочется дать пару советов:
- Внедряйте сообщение в случайные байты.
- Максимально уменьшайте объем внедряемой информации (вспоминаем дядюшку Хэмминга).
- Используйте ±1 кодирование.
- Выбирайте картинки с шумным LSB.
- UPD от remzalp: Используйте нигде не появлявшиеся изображения.
- Будьте паиньками!
Буду рада увидеть ваши предложения, дополнения, исправления и другой feedback!
P.S. Хочу выразить особую благодарность PavelMSTU за консультации и мотивационные пинки.
