В предыдущей статье "Скрещивание ужа и ежа.." мы проверяли применимость методов настройки систем автоматического управления к «реальным» моделям. В это статье попробуем оптимизировать не систему управления, а сам «физический» объект.

Для настройки регуляторов существует большое количество средств, методик и обеспечивающих оптимизацию законов регулирования. Если мы используем средства моделирования (типа Matlab Simulink), то можно сразу посмотреть на процесс оптимального управления непосредственно «вживую», на графиках. Возникает вопрос, если у нас есть метод для оптимизации параметров системы управления, можно ли оптимизировать не коэффициенты ПИД регулятора, а сам объект управления? Другими словами, не подбирать регуляторы для явно неудачной системы, а подобрать параметры самой системы. Ведь для компьютерной модели что коэффициенты ПИД, что размеры конструкции – это просто переменные, которые можно менять.
Немного теории «на пальцах»
Классическая задача оптимизации управления представлена на рисунке 1.
У нас есть модель объекта и модель регулятора. Мы задаем воздействие (необязательно ступенчатое). Создаем некоторую оценку переходного процесса и с помощью блока оптимизации настраиваем один или несколько параметров регулятора для получения наилучшей оценки. (см. рис. 1).

Рисунок 1. Классическая схема оптимизации регулятора.
При моделировании нам ничего не мешает менять не только параметры регулирования, но и параметры самой модели. Тогда в схеме оптимизации добавляется всего одна стрелка, которая меняет параметры самой модели (см. рис. 2).

Рисунок 2. Оптимизация параметров объекта.
Понятно, что если модель представлена в виде линейных передаточных функций, эта схема будет замечательно работать и подбирать параметры можно будет любым методом оптимизации. А если модель будет не линейная, а приближенная к жизни?
И, как всегда, совершенно случайно в мои руки попала «реальная» динамическая модель системы подачи топлива для вертолета. Ее и решено было немного оптимизировать.
Постановка задачи
Есть несколько баков вертолета различной конфигурации. Размеры баков, их конфигурации, а так же система трубопроводов, соединяющая эти баки, получены в результате компоновки вертолета. Схема системы представлена на рисунке 3. Баки соединены между собой по топливу и по инертному газу.
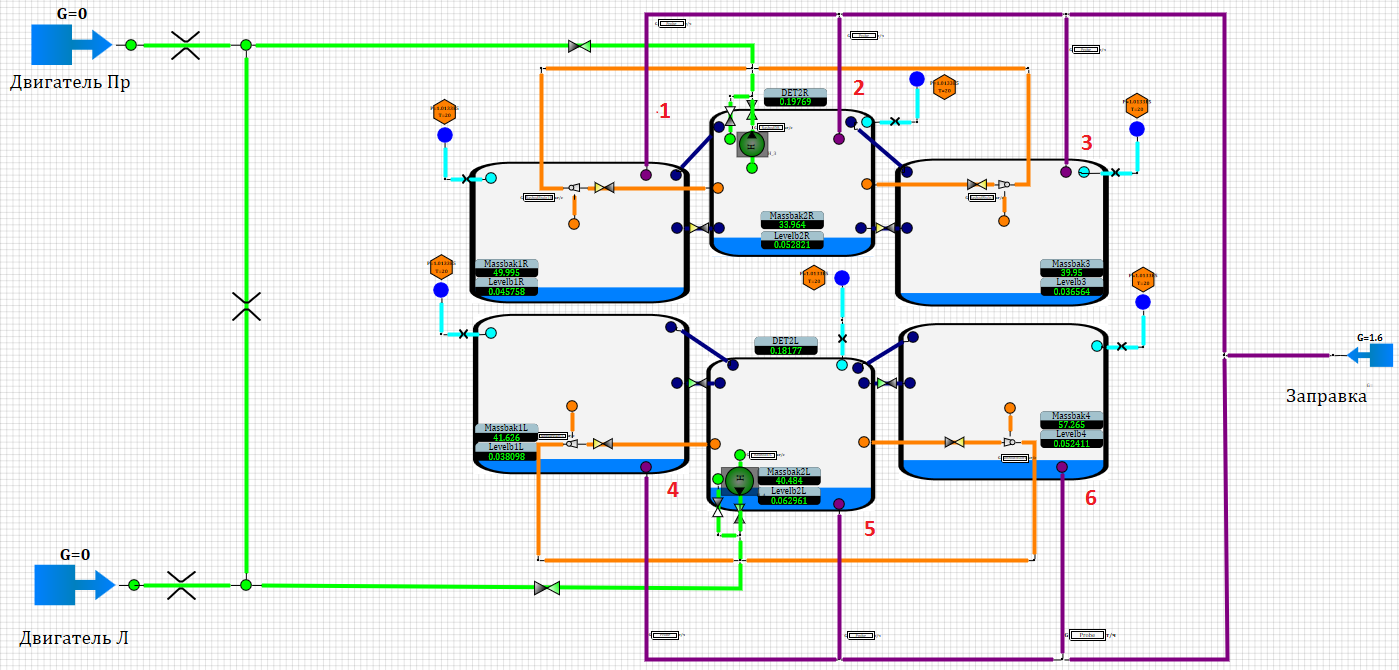
Рисунок 3. Модель топливной системы вертолета.
Диаметры трубопроводов могут быть от 10 до 70 мм. Задача: подобрать диаметр трубопроводов 1, 2, 3, 4, 5, 6, таким образом, чтобы обеспечить равномерную заправку баков из одного источника. Поскольку в результате компоновки вертолета баки оказались разными и тракты трубопроводов несимметричные, а так же существует система инертного газа, мы получаем задачу подбора диаметров по заданному расходу в каждый бак.
Рассмотрим несколько способов решения задачи:
Подбор диаметров простым регулятором.
Как было уже сказано выше, для компьютерной модели все эти разделения на систему управления и объект управления являются условными, ведь и то и другое – переменная в памяти компьютера, поэтому мы можем подключить регулятор таким образом, чтобы он воздействовал не на исполнительный механизм, а на диаметр трубопровода.
В жизни этого невозможно, но на модели пожалуйста. Схема для оптимизатора в этом случае выглядит так, как показано на рисунке 4.
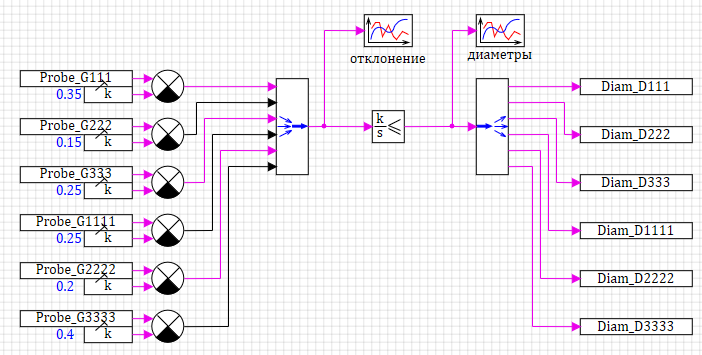
Рисунок 4. Подбор диметров с помощью интегрального регулятора.
Работает данная модель так:
Показания датчиков расхода в каждой линии сравниваются с заданными значениями. Разница подается на вход в векторный интегратор с ограничителями (6 независимых интеграторов). Если разница равна нулю, то на выходе из интегратора ничего не меняется, если разница больше нуля, то диаметр нужно уменьшать, если разница меньше нуля, то диаметр нужно увеличивать. На графики выводим текущее отклонение расхода от заданного в каждой линии, и диаметры трубопроводов.
Коэффициент интегратора определяет скорость изменения диаметра в процессе расчета.
Интегратор ограничен верхним и нижним значением диаметра трубопровода.
Начальное положение интегратора и, следовательно, начальный диаметр трубопровода приняты равным 10 мм. (0.01)
Параметры векторного интегратора приведены на рисунке 5.

Рисунок 5. Настройки интегратора для подбора диаметров.
Запускаем модель и видим следующий результат: в течении 40 секунд наш «виртуальный регулятор» подобрал диаметры трубопроводов, таким образом чтобы расходы были равны заданным.
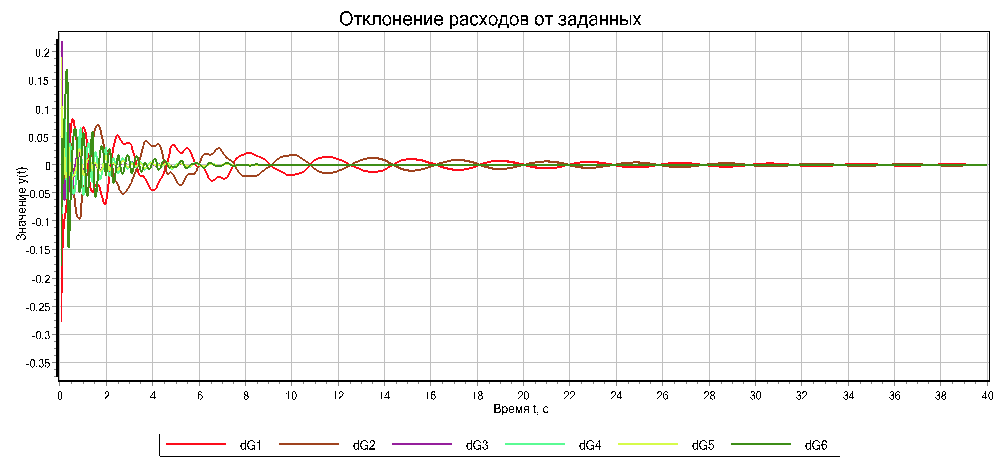
Рисунок 6. Отклонения расходов.
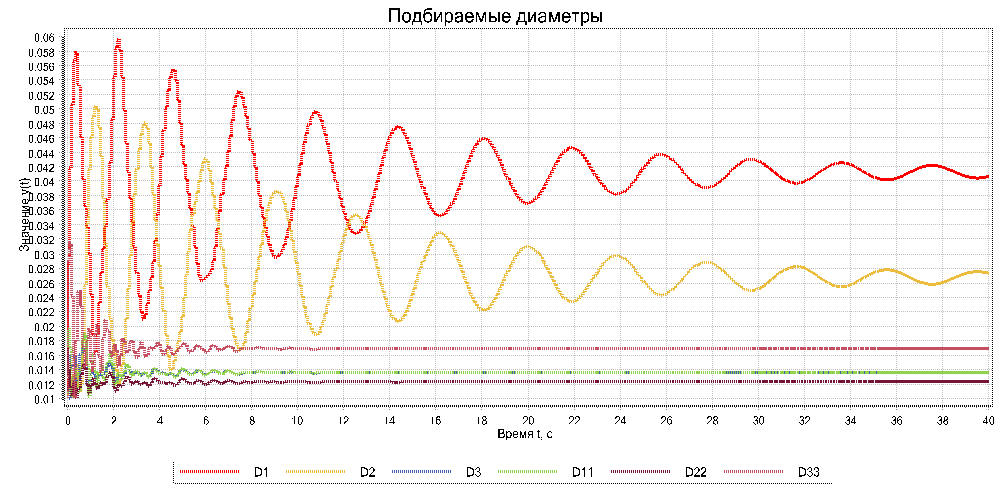
Рисунок 7. Подбор диаметров.
По графику видно, что наибольшие колебания и более долгое время установления – для первых двух диаметров. Если изменить коэффициент интегрирования с -1, до -0,5, то настройка происходит еще быстрее. Уже за 4 секунды расходы устанавливаются в нужное значение. См. рис. 8.

Рисунок 8. Отклонения расходов от заданных при Ki = -0.5.
Преимущества оптимизации регулятором:
- Простота и наглядность.
- Скорость проведения оптимизации определяется скоростью динамического расчета модели.
Недостатки оптимизации регулятором:
- Можно использовать только, если есть однозначная и очевидная связь между измеряемым и изменяемым параметрами. Как в нашем примере больше диаметр – больше расход.
- Дополнительные регуляторы могут вызвать колебания в системе. Например, в нашем случае если коэффициент интегратора принять равным – 2, то система переходит в режим колебаний (см. рис 9).
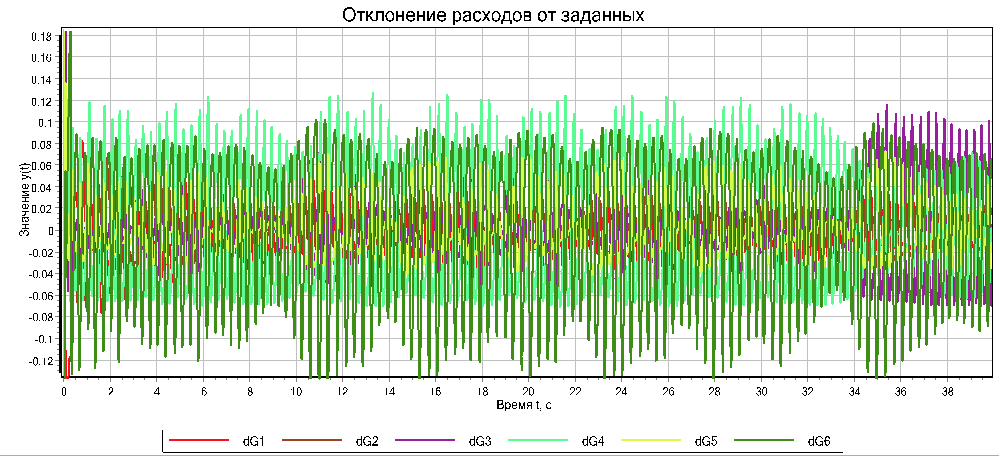
Рисунок 9. Отклонения расходов от заданных при Ki = — 2.
Подбор параметром блоком оптимизации.
Когда у нас нет очевидной связи между измеренными параметрами и затруднительно определить воздействие, необходимо использовать специальные блоки оптимизации. В нашем случае схема практически не изменится. В качестве критерия оптимизации мы используем модуль отклонения расходов от заданных, и тогда в схеме вместо интегратора появится блок оптимизации. Общая схема оптимизации будет выглядеть как показано на рисунке 10.

Рисунок 10. Схема подбора диаметров с помощью блока оптимизации.
Работает данная модель так:
Показания датчиков расхода в каждой линии сравниваются с заданными значениями. Используя блок модуля, вектор отклонений преобразуется в вектор абсолютных отклонений.
Таким образом, критерием оптимизации становится равенство нулю отклонений. Ну, а в качестве настраиваемых параметров выступают диаметры трубопроводов.
Оптимизация может работать в двух режимах:
- оптимизация по полному переходному процессу. Когда для расчёта критерия оптимизации нужно выполнить полное моделирование всего процесса.
- оптимизация «на ходу». Когда критерий оптимизации рассчитывается через определенный временной шаг.
Оптимизация по полному переходному процессу требует многочисленных повторений и занимает много времени, поэтому остановимся на оптимизации «на ходу». По умолчанию оптимизация выполняется с периодичностью раз в секунду. Настройки блока оптимизации приведены на рисунке 11.

Рисунок 11. Настройка блока оптимизации.
Запускаем на расчет и смотрим на результат. За 70 секунд процесса выполнить оптимизацию не удалось. Хотя, судя по графику, происходит постепенное схождение. см. рис. 12.

Рисунок 12. Отклонения расходов оптимизация с периодом 1 сек.
Похоже, что если осуществлять расчет оптимальных параметров чаще, можно быстрее прийти к решению. Для выбора периодичности оптимизации необходимо учитывать запаздывание отклика системы в динамическом режиме расчета. После изменения диаметра должно пройти какое то время, чтобы эти изменения отразились на измеряемых параметрах. Если посмотреть на график изменений расходов в более узком временном диапазоне, (см. рис. 13), то видно, что после изменения диаметра новый расход устанавливается примерно за 0.5 секунды.
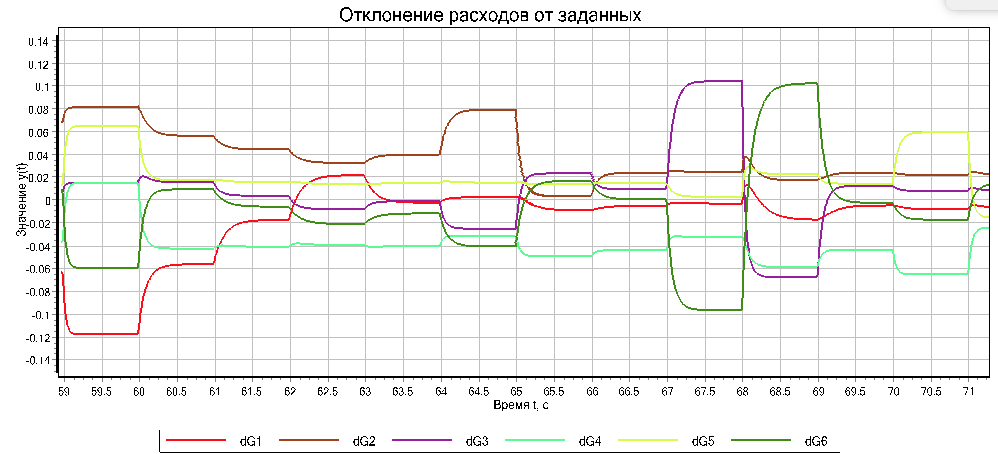
Рисунок 13. Отклонения расходов оптимизация с периодом 1 сек.
Уменьшим периодичность анализа с 1 до 0.5 секунду. Таким образом, за то же время количество расчётов увеличится в 2 раза. В результате удается произвести оптимизацию диаметров трубопроводов за 70 секунд динамического процесса. На графике 14 видно, что метод оптимизации работает. И отклонения расходов стремтся к нулю.
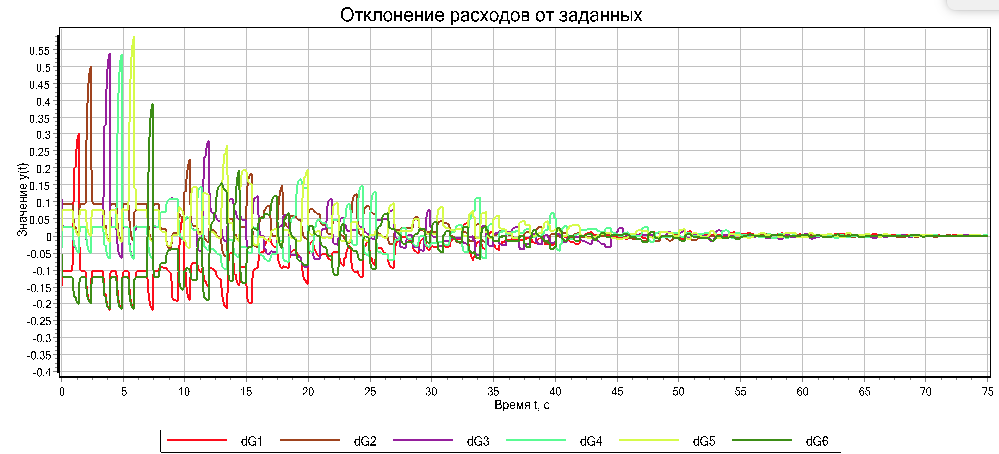
Рисунок 14. Отклонения расходов оптимизация с периодом 0.5 сек.

Рисунок 15. Побор диаметров оптимизацией.
Вывод
Эксперимент с подробной физической моделью топливной показал, что можно использовать методы теории автоматического регулирования, не только для настройки и оптимизации систем управления, но и для оптимизации физических параметров модели.