Часть 0: Фракталы в простых числах.
Часть 1: Фракталы в иррациональных числах.

В статье присутствуют Gif и контрастные картинки. У эпилептиков может случиться эпилептический припадок.
В предыдущей статье мы рассмотрели алгоритм визуализации двоичных последовательностей. Давайте вспомним.
Берем двоичную последовательность. В качестве примера несколько первых бит фрактальной последовательности, рассмотренной в предыдущей статье:
0100110110010011001001101100
Рисуем квадратное клеточное поле. Расставляем биты у верхней границы. Расстояние между битами — две клетки:

Для каждого бита рисуем по диагонали пунктирную траекторию (через клетку). Для нулей первый штрих рисуем вправо:

Для единиц — влево:
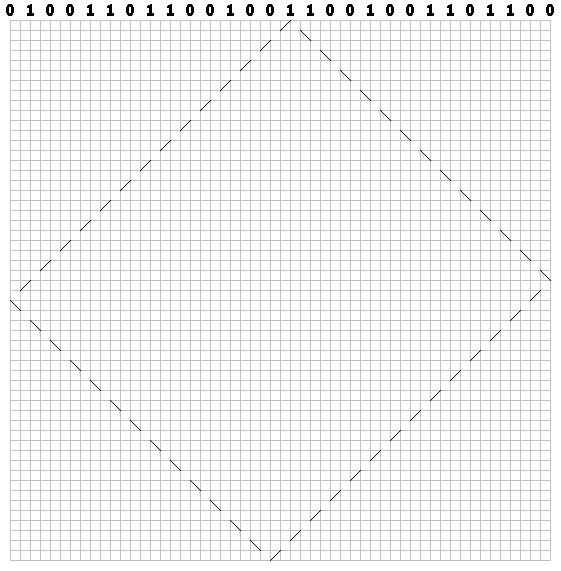
Нарисовали траекторию для каждого бита. Получили «бильярдный» паттерн:

Идентичный паттерн (без дефекта по диагонали — последовательность бесконечная, мы же ее визуализировали как конечную последовательность) можно получить другим способом. Инвертируем каждый четный бит в последовательности:
0001100011000110011100111001
Далее для каждого бита рисуем вертикальные пунктирные линии:

Расставляем биты слева, рисуем горизонтальные линии:

Совмещаем:

После написания первой статьи, оставались нерешенными два вопроса:
1. Можно ли нарисовать фрактальный паттерн для иррациональных чисел. Можно. Вопрос решили в предыдущей статье. На картинке выше — часть фрактального паттерна для . Если выделить одну из кривых на этом паттерне:
. Если выделить одну из кривых на этом паттерне:

Получим известную фрактальную кривую — «Fibonacci word fractal».
2. Второй вопрос — можно ли написать алгоритм, закрашивающий паттерн:

Решением второго вопроса займемся в этой статье. Раскрашивать паттерны будем с помощью ткацкого станка, работу которого сымитируем с помощью JavaScript.
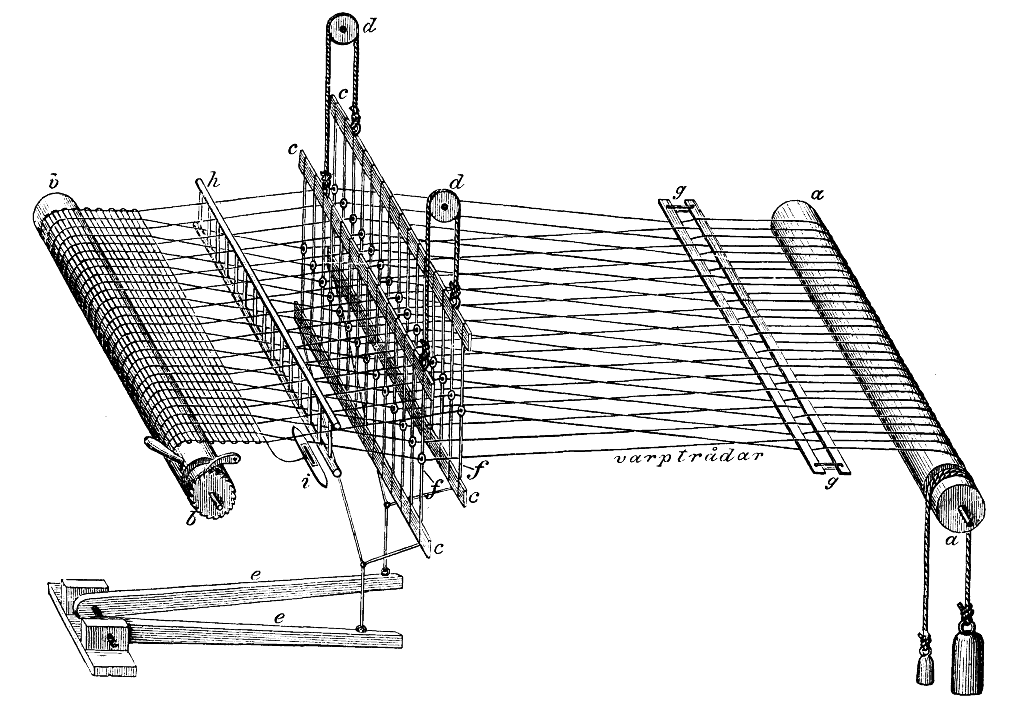
На схеме выше — самый простой станок. Он состоит из двух рамок, через которые протянуты нити. Рамки соединены с педалями. При нажатии на одну из педалей, одна из рамок поднимается. Нити, протянутые через эту рамку поднимаются и в получившийся зазор между нитями протягивается поперечная нить. Если четные и нечетные нити протянуть через разные рамки — получается переплетение в шахматном порядке:

В более сложных станках используется от четырех и больше рамок:

Ashford 4 Shaft Table Loom
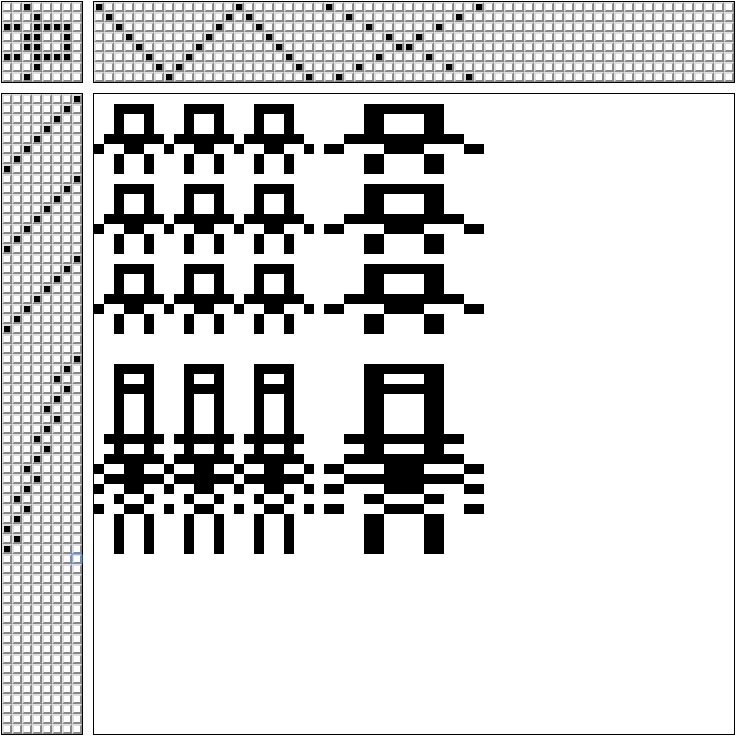
Для того, чтобы не запутаться, какую педаль нажимать — составляют схему.
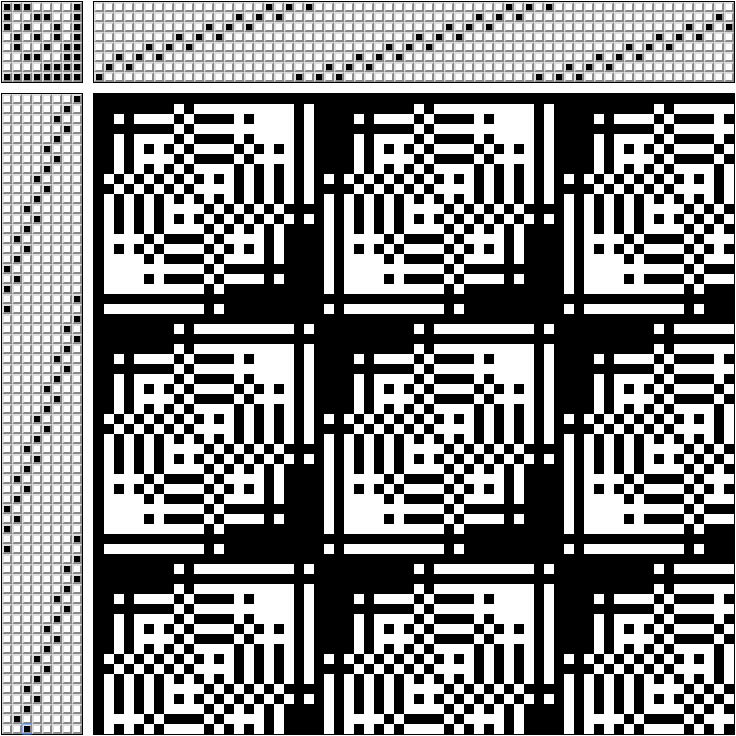
В верхней правой части схемы отмечено, через какие рамки проходят нити (схема для ткацкого станка на 8 рамок).
В левом верхнем углу — какие педали зажимать одновременно (каждая педаль связана только со своей рамкой).
В левой нижней части — в каком порядке зажимать педали.
В правой нижней части — какое переплетение мы получим. Если протягивать белую нить через черные — получим монохромный узор.
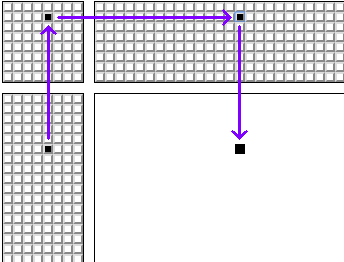
Сходу «въехать» в принцип может показаться немного затруднительным. На картинке ниже показано, как формируется ткацкий узор:

Напишем скрипт. Протягивать нити через рамки будем с помощью одномерного массива array2. В одномерный массив array1 запишем очередность зажатия педалей. В array3 (бинарный массив 8х8) запишем, какие педали зажимать одновременно.
Скрипт (работает в Google Chrome).
С помощью нашего импровизированного ткацкого станка мы можем нарисовать самые разнообразные узоры:
Но так исторически сложилось, что у среднестатистического человека не больше двух ног. Поэтому удобно одновременно зажимать не больше двух педалей. Один из самых популярных шаблонов для ткацкого станка выглядит следующим образом:
Для 4-х рамок. И его модификация для 8-ми рамок:

Неожиданно, узоры (или фрагмент узоров) сделанные с помощью этого шаблона, похожи на наши «бильярдные» паттерны. Кроме того, эти узоры получаются закрашенными:

Можно научиться подбирать «бильярдные» паттерны для ткацкого станка. Пример:

В начале статьи мы уже видели фрагмент этого паттерна.
Закончим с ткацкими станками и напишем скрипт для визуализации двоичных последовательностей. От одного из массивов можем избавиться — паттерн симметричен по диагонали. Как заполнить оставшийся массив? Элементарно:

Берем последовательность для . Создаем массив. В нулевой элемент массива записываем нулевой бит последовательности. Поочередно берем каждый бит последовательности. Если n-й бит = 1 — записываем в массив a[n]=a[n-1]+1. Если бит = 0 — записываем a[n]=a[n-1]-1
. Создаем массив. В нулевой элемент массива записываем нулевой бит последовательности. Поочередно берем каждый бит последовательности. Если n-й бит = 1 — записываем в массив a[n]=a[n-1]+1. Если бит = 0 — записываем a[n]=a[n-1]-1
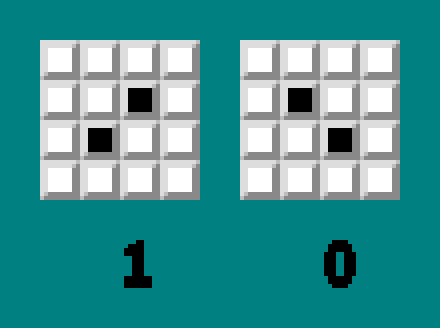
Проверяем:

Фактически мы уже получили элементарный фрактал, но продолжим.
Далее разберемся с матрицей:

Суммируем и
и  . Делим по модулю на 4. Если получившийся результат = 0 или 1 — записываем в матрицу true. Для 2 и 3 записываем false. Можем обойтись без матрицы (заранее неизвестно, какие максимальные и минимальные значения принимает a[n]). Суммируем a[x] и a[y]. К получившейся сумме добавляем некоторое число
. Делим по модулю на 4. Если получившийся результат = 0 или 1 — записываем в матрицу true. Для 2 и 3 записываем false. Можем обойтись без матрицы (заранее неизвестно, какие максимальные и минимальные значения принимает a[n]). Суммируем a[x] и a[y]. К получившейся сумме добавляем некоторое число  (чтобы избавиться от тех случаев, когда сумма — отрицательное число). Делим по модулю на 4. Для значений 0 и 1 закрашиваем пиксель с координатами
(чтобы избавиться от тех случаев, когда сумма — отрицательное число). Делим по модулю на 4. Для значений 0 и 1 закрашиваем пиксель с координатами  и
и  .
.
Окончательный алгоритм занимает всего несколько строк:
Визуализируем наши фрактальные последовательности.

Можно легко модифицировать скрипт для того, чтобы получить RGB-изображение:

Выше мы к сумме a[x]+a[y] прибавляли некоторое число . Если не прибавлять это число — минимальное значение суммы = -8, максимальное = 8 (для
. Если не прибавлять это число — минимальное значение суммы = -8, максимальное = 8 (для  и
и  от 0 до 750). Если убрать
от 0 до 750). Если убрать  — в некоторых случаях сумма получается отрицательной и не кратной 4-м и для этих случаев пиксель не закрашивается (остается черным):
— в некоторых случаях сумма получается отрицательной и не кратной 4-м и для этих случаев пиксель не закрашивается (остается черным):

Можно представить это так, будто часть фрактала находится ниже некоторой мнимой границы (ниже этой границы закрашиваются только отрицательные значения кратные 4-м: -4, -8, -12, ...).
Можем посмотреть, где находится эта граница:

Вместо деления по модулю, можем сравнить сумму с некоторым определенным значением и тем самым закрасить только один «слой» фрактала. В качестве примера возьмем среднее между минимальным и максимальным значением:

Изменяя значения от минимального до максимального, можем посмотреть как меняются «слои» в динамике:

Кроме того, мы можем «в лоб» сравнить a[x] с a[y] и тоже получить фрактальный паттерн:

Следующая последовательность:
Фрактал:

RGB:

Средний слой:

В динамике:

Фрактал:

RGB:

Средний слой:

В динамике:

Фрактал:

RGB:

Средний слой:

В динамике:
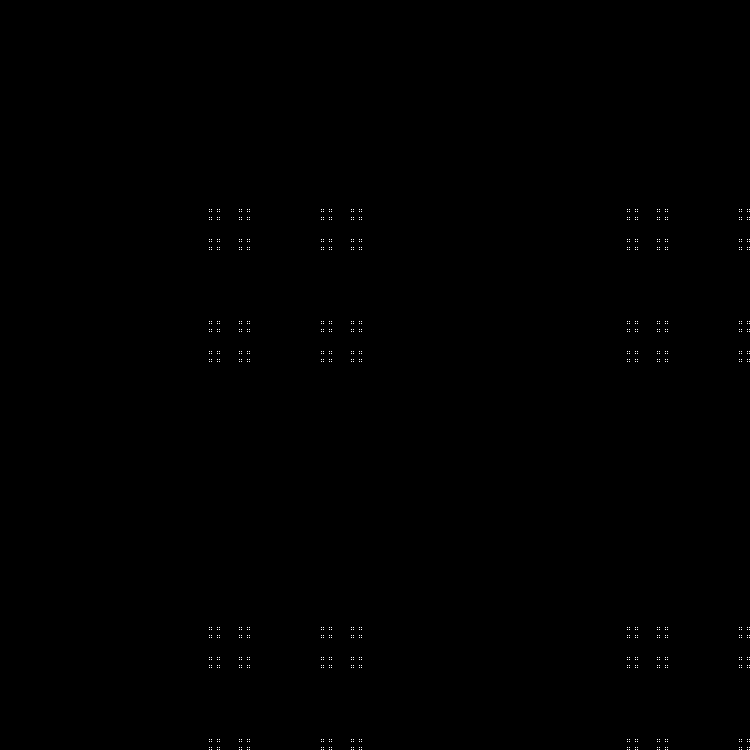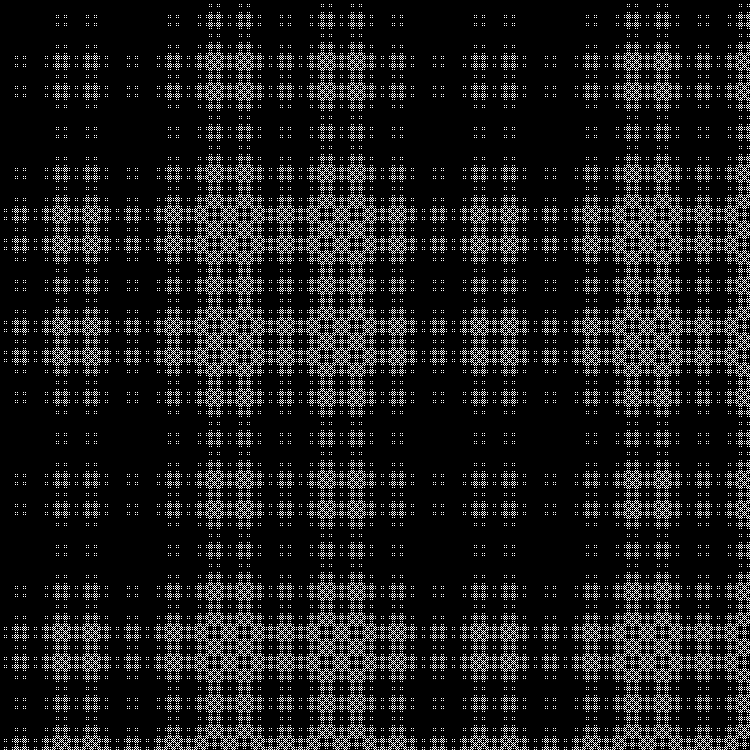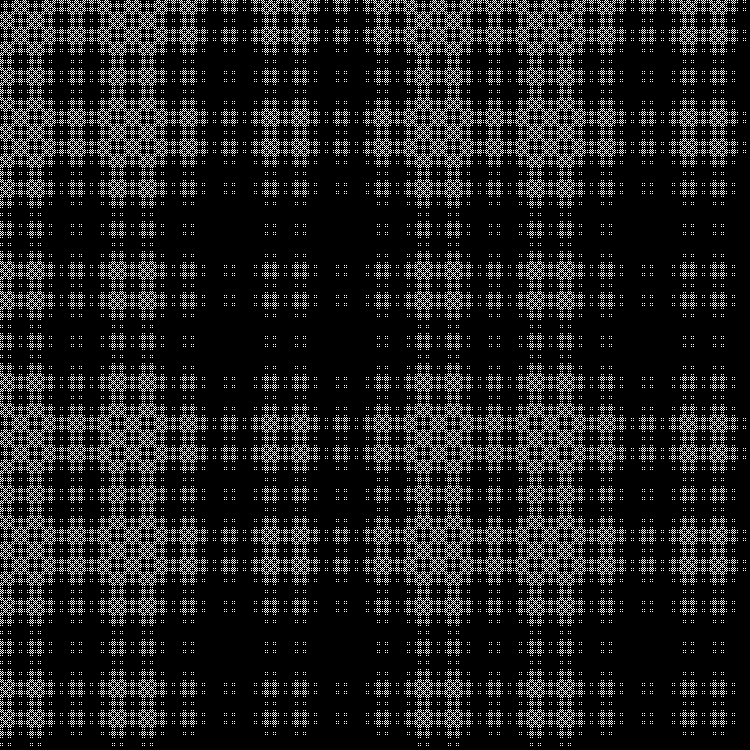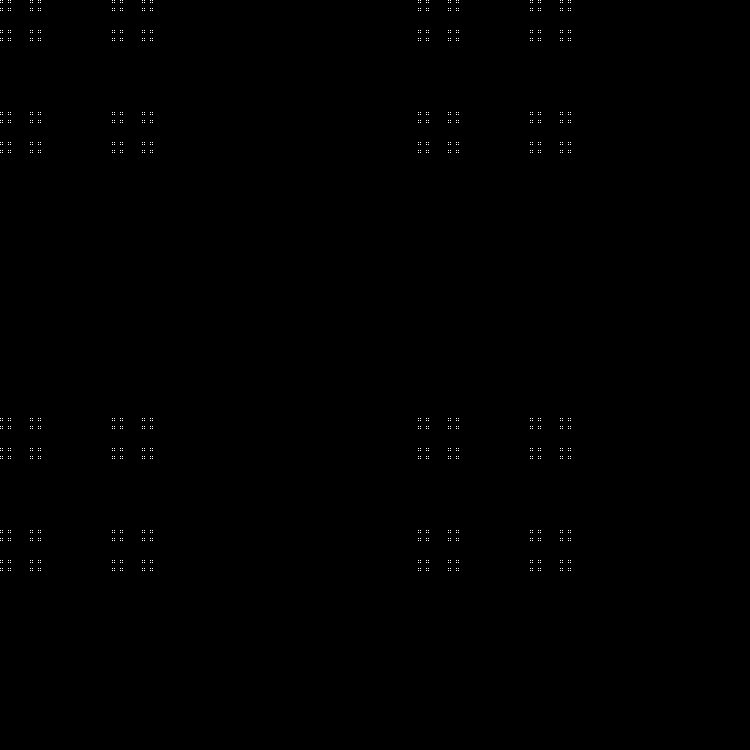
Фрактал:

RGB:

Средний слой:

В динамике:

Ну и наш любимый фрактал (часть этого паттерна можно нарисовать с помощью бильярда, с размерами сторон равными числам Фибоначчи):
Фрактал:

RGB:

Средний слой:

В динамике:
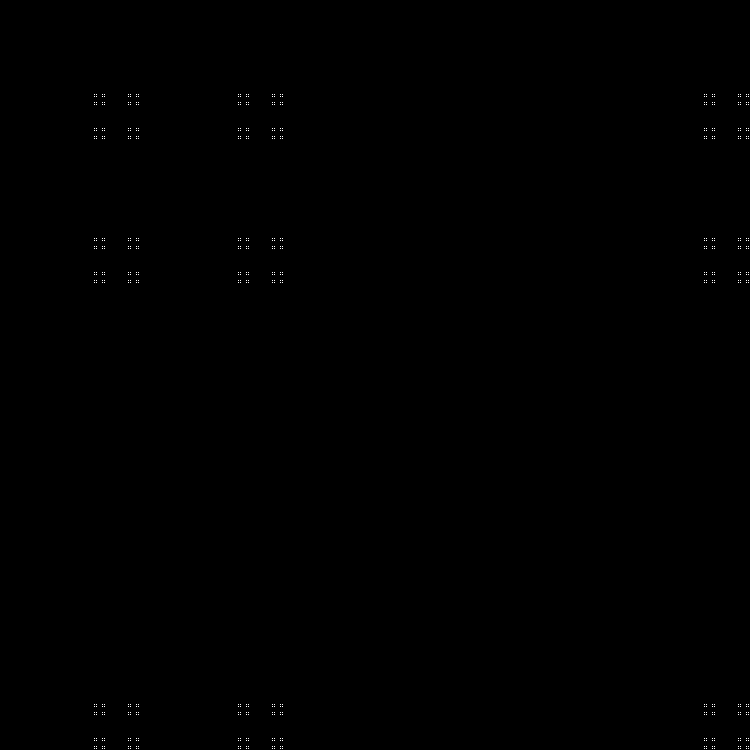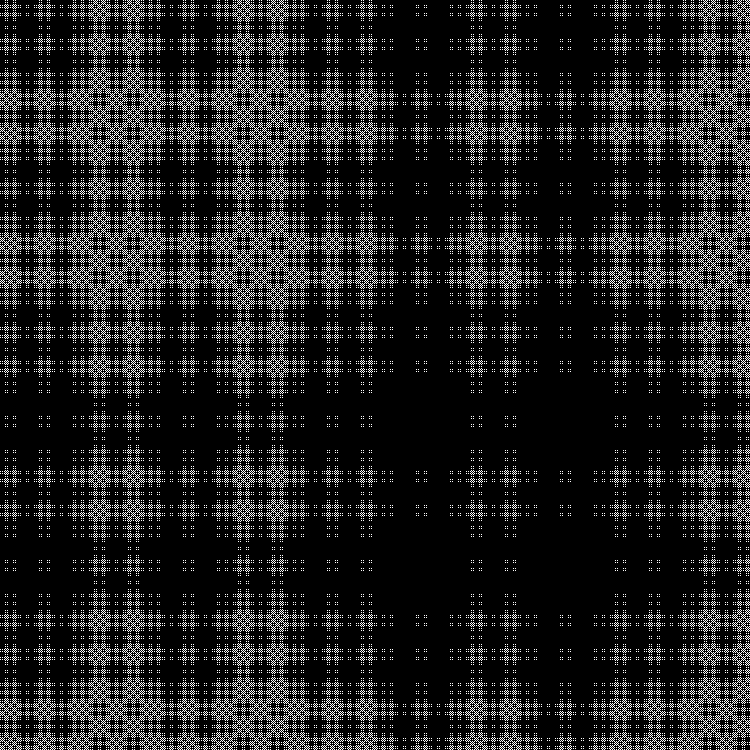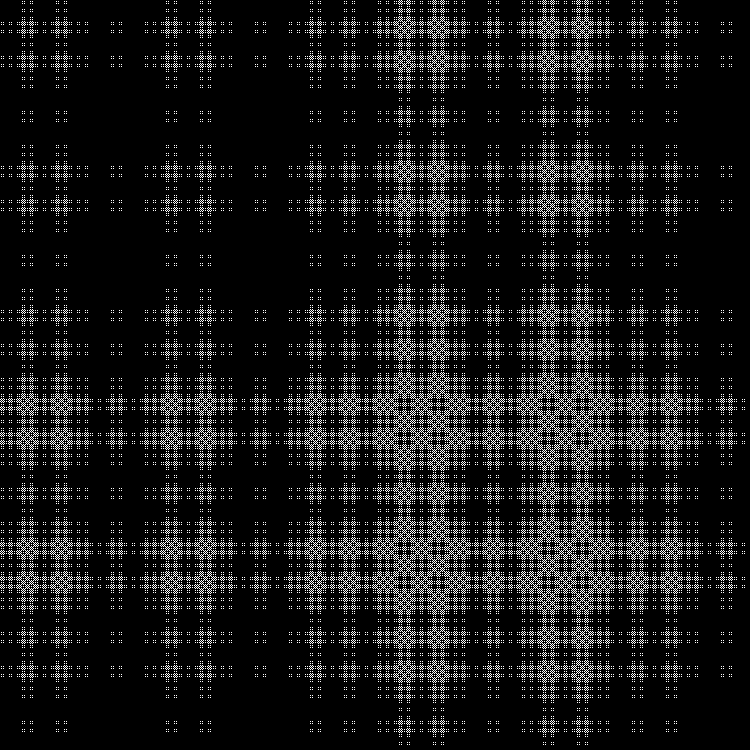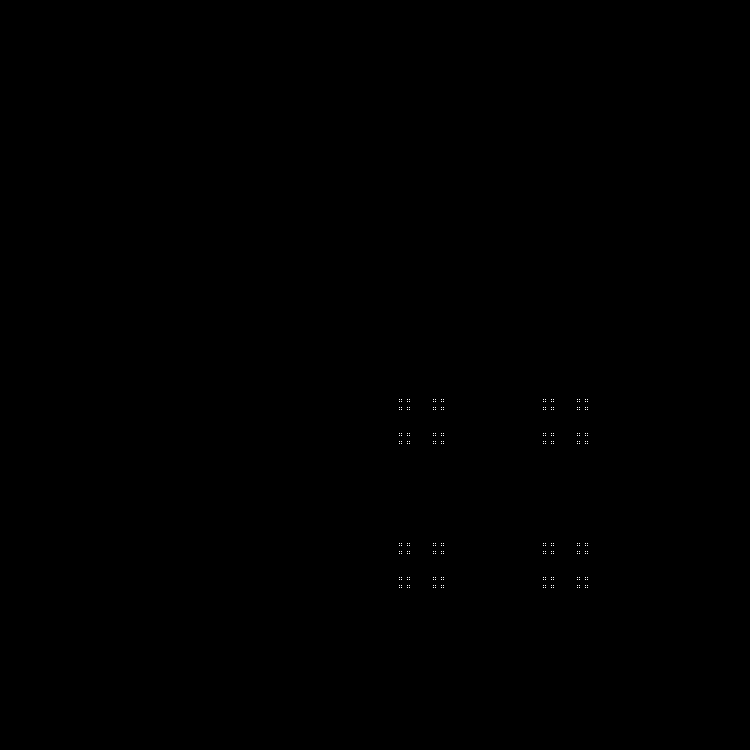
Еще одна последовательность в завершение:
Паттерн:

RGB:

Средний слой:

В динамике:
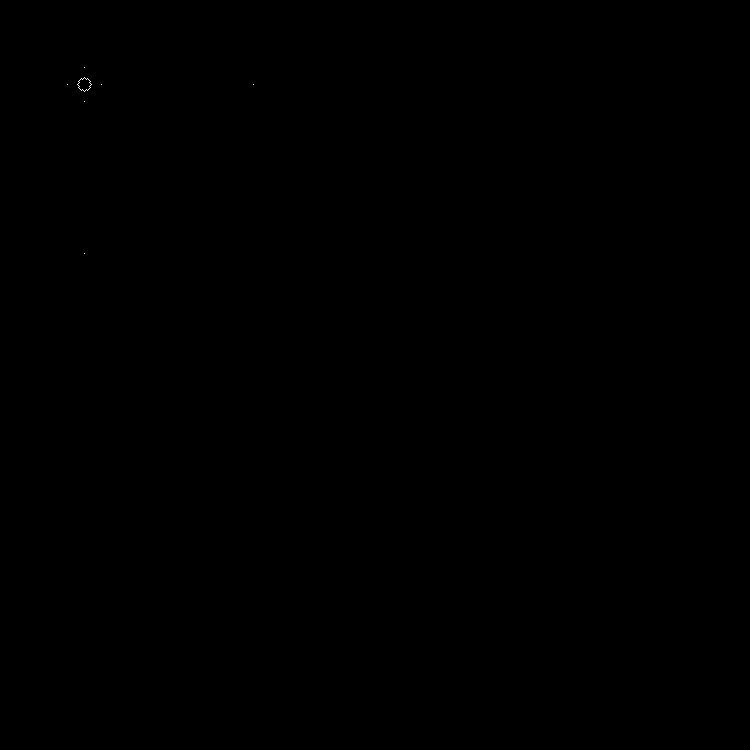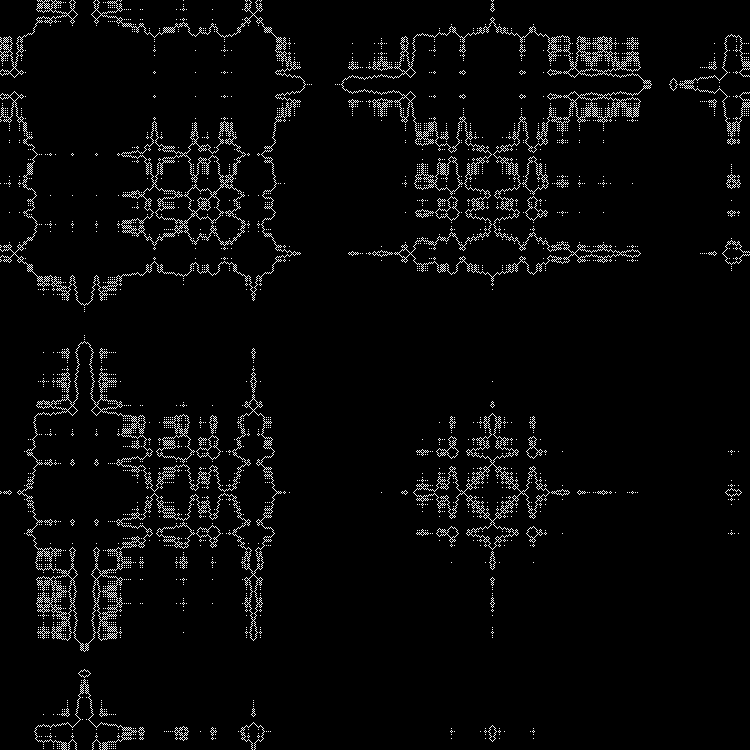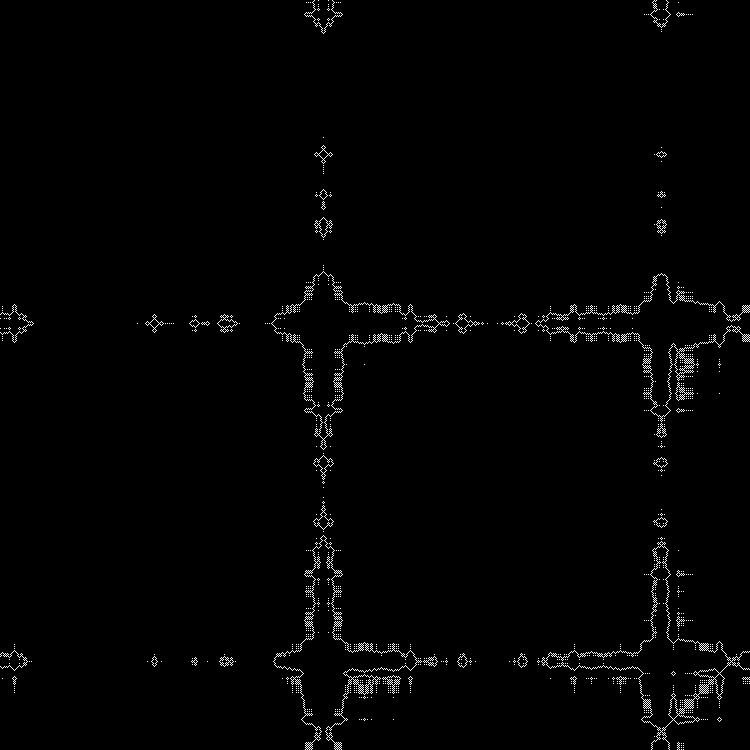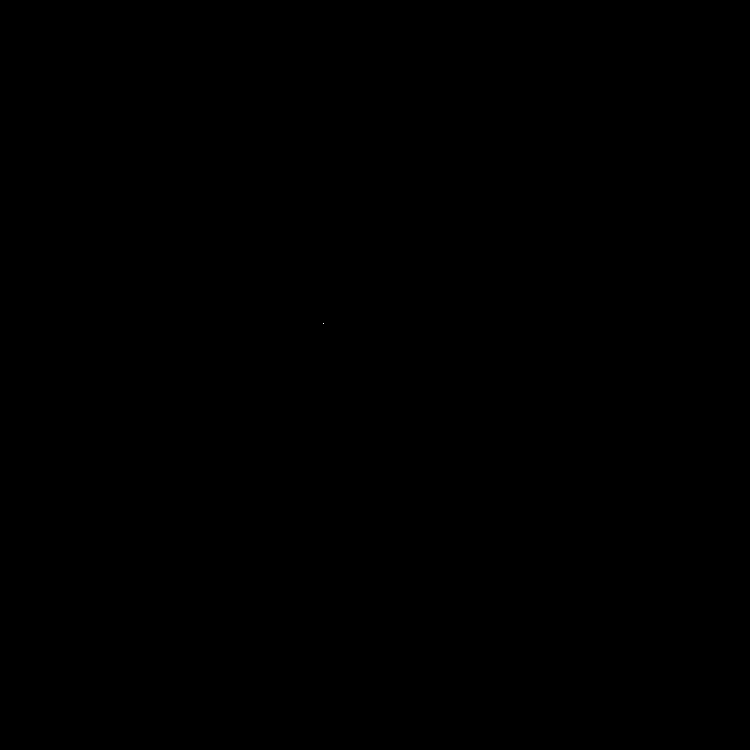
Другие квадратные корни можно вбить в скрипт. (Можно вбивать дробные значения).
Во втором скрипте можно вбить последовательность вручную.
Еще один скрипт для бильярдов. Координаты мышки — размеры бильярда. Паттерн в левой части формируется из последовательности, полученной с помощью остатков от деления (подробности в предыдущей статье). В правой части — четность .
.
Часть 1: Фракталы в иррациональных числах.

В статье присутствуют Gif и контрастные картинки. У эпилептиков может случиться эпилептический припадок.
В предыдущей статье мы рассмотрели алгоритм визуализации двоичных последовательностей. Давайте вспомним.
Берем двоичную последовательность. В качестве примера несколько первых бит фрактальной последовательности, рассмотренной в предыдущей статье:
0100110110010011001001101100
Рисуем квадратное клеточное поле. Расставляем биты у верхней границы. Расстояние между битами — две клетки:

Для каждого бита рисуем по диагонали пунктирную траекторию (через клетку). Для нулей первый штрих рисуем вправо:

Для единиц — влево:

Нарисовали траекторию для каждого бита. Получили «бильярдный» паттерн:

Идентичный паттерн (без дефекта по диагонали — последовательность бесконечная, мы же ее визуализировали как конечную последовательность) можно получить другим способом. Инвертируем каждый четный бит в последовательности:
0001100011000110011100111001
Далее для каждого бита рисуем вертикальные пунктирные линии:

Расставляем биты слева, рисуем горизонтальные линии:

Совмещаем:

После написания первой статьи, оставались нерешенными два вопроса:
1. Можно ли нарисовать фрактальный паттерн для иррациональных чисел. Можно. Вопрос решили в предыдущей статье. На картинке выше — часть фрактального паттерна для

Получим известную фрактальную кривую — «Fibonacci word fractal».
2. Второй вопрос — можно ли написать алгоритм, закрашивающий паттерн:

Решением второго вопроса займемся в этой статье. Раскрашивать паттерны будем с помощью ткацкого станка, работу которого сымитируем с помощью JavaScript.

На схеме выше — самый простой станок. Он состоит из двух рамок, через которые протянуты нити. Рамки соединены с педалями. При нажатии на одну из педалей, одна из рамок поднимается. Нити, протянутые через эту рамку поднимаются и в получившийся зазор между нитями протягивается поперечная нить. Если четные и нечетные нити протянуть через разные рамки — получается переплетение в шахматном порядке:

В более сложных станках используется от четырех и больше рамок:

Ashford 4 Shaft Table Loom
Для того, чтобы не запутаться, какую педаль нажимать — составляют схему.

В верхней правой части схемы отмечено, через какие рамки проходят нити (схема для ткацкого станка на 8 рамок).
В левом верхнем углу — какие педали зажимать одновременно (каждая педаль связана только со своей рамкой).
В левой нижней части — в каком порядке зажимать педали.
В правой нижней части — какое переплетение мы получим. Если протягивать белую нить через черные — получим монохромный узор.
Сходу «въехать» в принцип может показаться немного затруднительным. На картинке ниже показано, как формируется ткацкий узор:

Напишем скрипт. Протягивать нити через рамки будем с помощью одномерного массива array2. В одномерный массив array1 запишем очередность зажатия педалей. В array3 (бинарный массив 8х8) запишем, какие педали зажимать одновременно.

for(var i=0;i<length;i++){
for(var j=0;j<length;j++){
if(array3[array1[i]][array2[j]]){
context.fillRect(i, j, 1, 1);
}
}
}
Скрипт (работает в Google Chrome).
С помощью нашего импровизированного ткацкого станка мы можем нарисовать самые разнообразные узоры:

Но так исторически сложилось, что у среднестатистического человека не больше двух ног. Поэтому удобно одновременно зажимать не больше двух педалей. Один из самых популярных шаблонов для ткацкого станка выглядит следующим образом:

Для 4-х рамок. И его модификация для 8-ми рамок:

Неожиданно, узоры (или фрагмент узоров) сделанные с помощью этого шаблона, похожи на наши «бильярдные» паттерны. Кроме того, эти узоры получаются закрашенными:

Можно научиться подбирать «бильярдные» паттерны для ткацкого станка. Пример:

В начале статьи мы уже видели фрагмент этого паттерна.
Закончим с ткацкими станками и напишем скрипт для визуализации двоичных последовательностей. От одного из массивов можем избавиться — паттерн симметричен по диагонали. Как заполнить оставшийся массив? Элементарно:

Берем последовательность для

var a=[0];
for(var i=1;i<size;i++){
if(Math.floor(i*Math.sqrt(2))%2==1)
a[i]=a[i-1]+1;
else
a[i]=a[i-1]-1;
}
Проверяем:
for(var i=0;i<size;i++){
context.fillRect(i, a[i]+50, 1, 1);
}

Фактически мы уже получили элементарный фрактал, но продолжим.
Далее разберемся с матрицей:

Суммируем
Окончательный алгоритм занимает всего несколько строк:
var a=[0];
for(var i=1;i<size;i++){
if(Math.floor(i*Math.sqrt(2))%2==1)
a[i]=a[i-1]+1;
else
a[i]=a[i-1]-1;
}
for(var x=0;x<size;x++){
for(var y=0;y<size;y++){
q=(a[x]+a[y]+512)%4;
if(q==0 || q==1) context.fillRect(x, y, 1, 1);
}
}
Визуализируем наши фрактальные последовательности.

Можно легко модифицировать скрипт для того, чтобы получить RGB-изображение:
q=(a[x]+a[y]+512)%4;
/*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/
if(q==0) context.fillStyle = 'rgb(255,0,0)';
if(q==1) context.fillStyle = 'rgb(0,255,0)';
if(q==2) context.fillStyle = 'rgb(0,0,255)';
if(q==3) context.fillStyle = 'rgb(0,0,0)';
context.fillRect(x, y, 1, 1);

Выше мы к сумме a[x]+a[y] прибавляли некоторое число
q=(a[x]+a[y])%4;
if(q==0 || q==1) context.fillRect(x, y, 1, 1);

Можно представить это так, будто часть фрактала находится ниже некоторой мнимой границы (ниже этой границы закрашиваются только отрицательные значения кратные 4-м: -4, -8, -12, ...).
Можем посмотреть, где находится эта граница:
if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1);

Вместо деления по модулю, можем сравнить сумму с некоторым определенным значением и тем самым закрасить только один «слой» фрактала. В качестве примера возьмем среднее между минимальным и максимальным значением:
q=(a[x]+a[y]);
if(q==0) context.fillRect(x, y, 1, 1);

Если не понятно

Изменяя значения от минимального до максимального, можем посмотреть как меняются «слои» в динамике:

Если не понятно
Настоятельно не рекомендую открывать спойлер, если у вас эпилепсия

Кроме того, мы можем «в лоб» сравнить a[x] с a[y] и тоже получить фрактальный паттерн:
if(a[x]==a[y]) context.fillRect(x, y, 1, 1);
Следующая последовательность:
Фрактал:

RGB:

Средний слой:

В динамике:

Фрактал:

RGB:

Средний слой:

В динамике:

Фрактал:

RGB:

Средний слой:

В динамике:
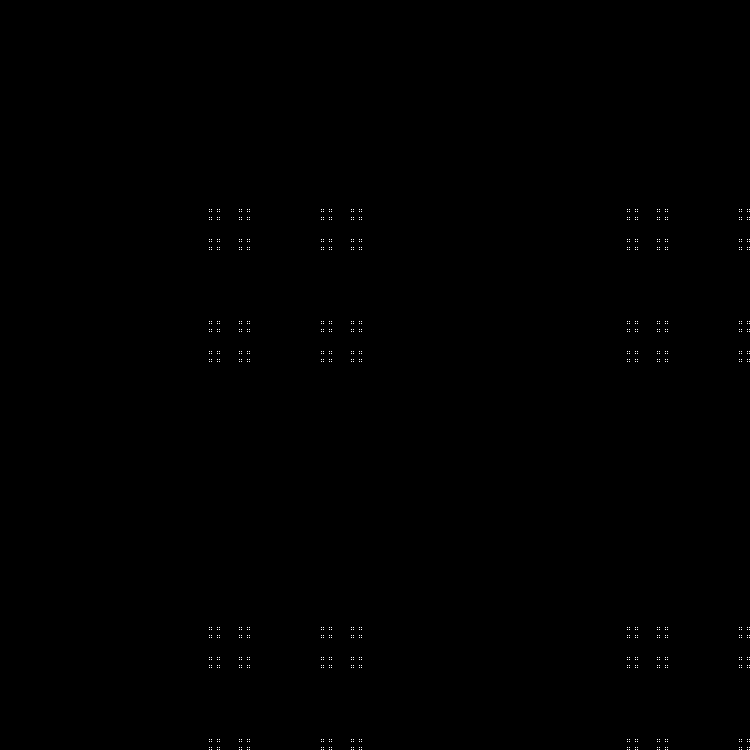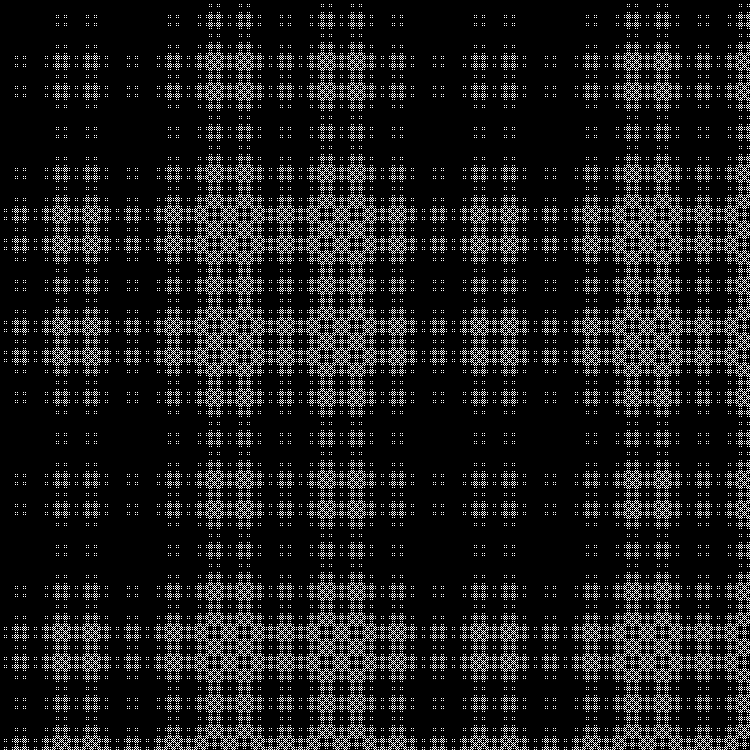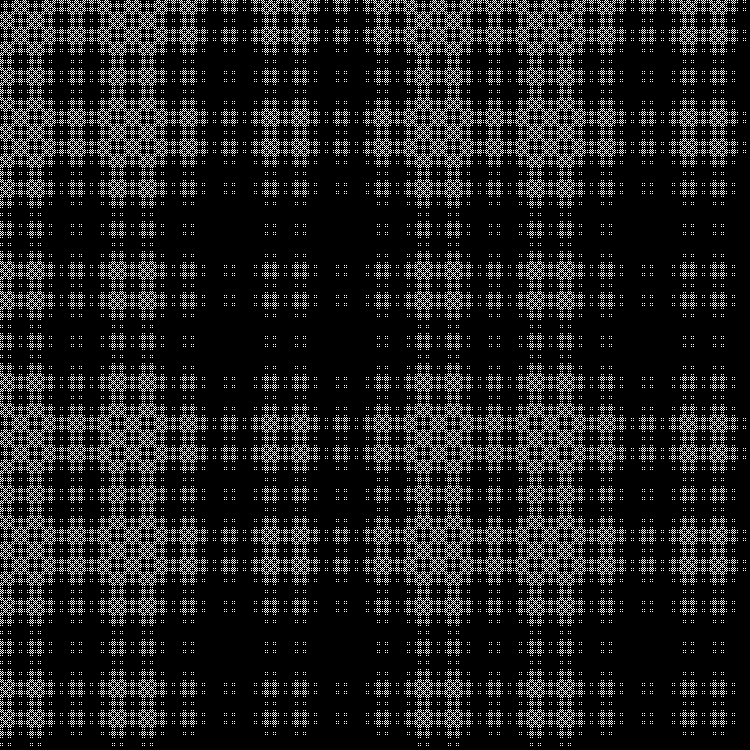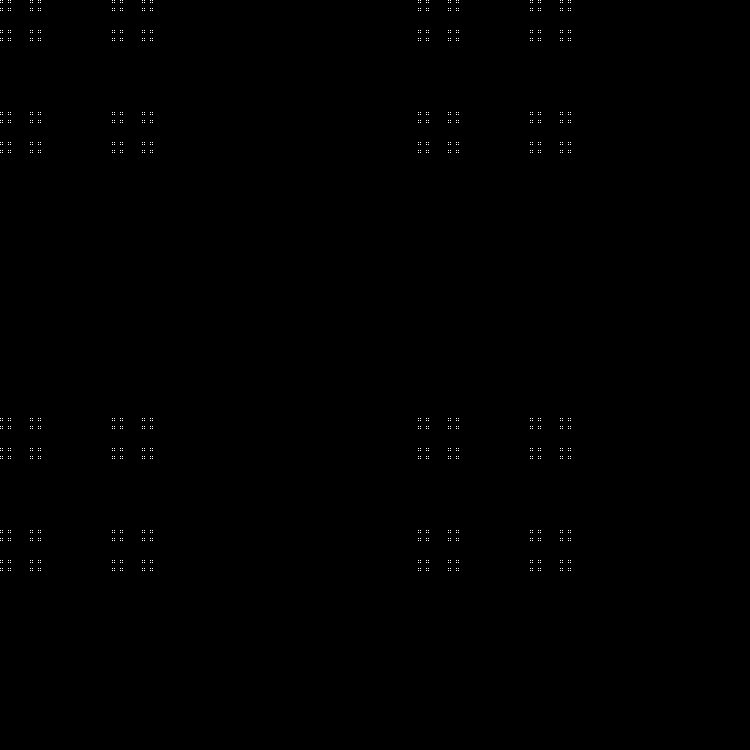
Фрактал:

RGB:

Средний слой:

В динамике:

Ну и наш любимый фрактал (часть этого паттерна можно нарисовать с помощью бильярда, с размерами сторон равными числам Фибоначчи):
Фрактал:

RGB:

Средний слой:

В динамике:
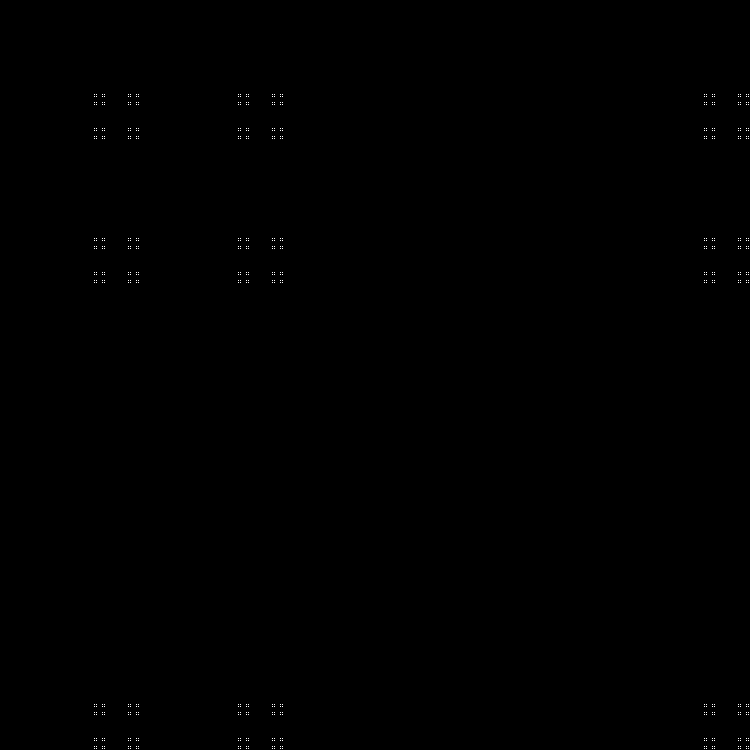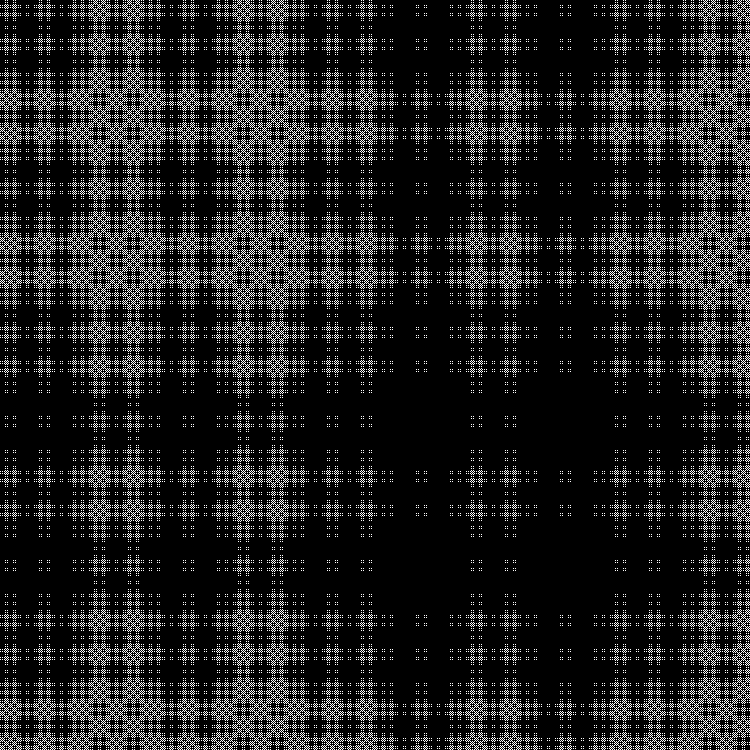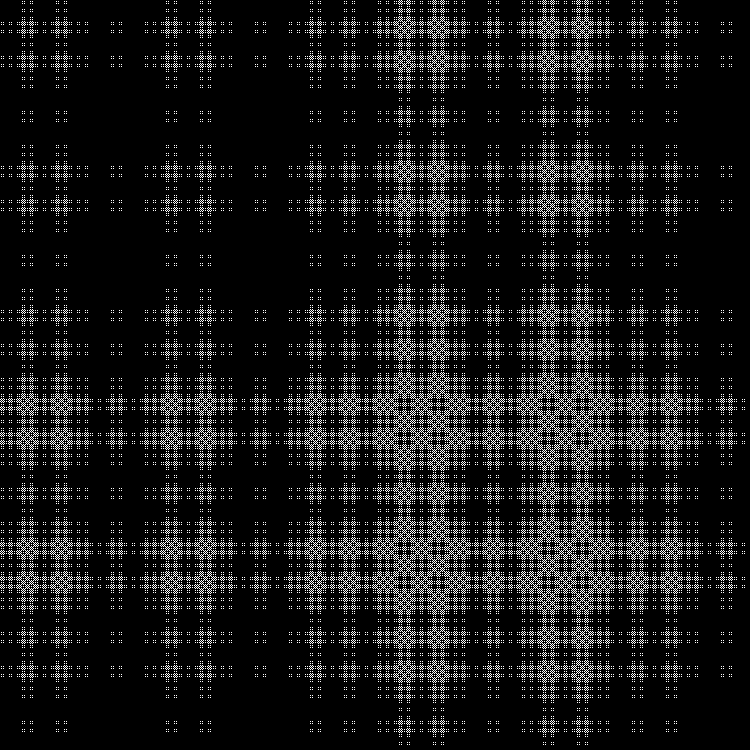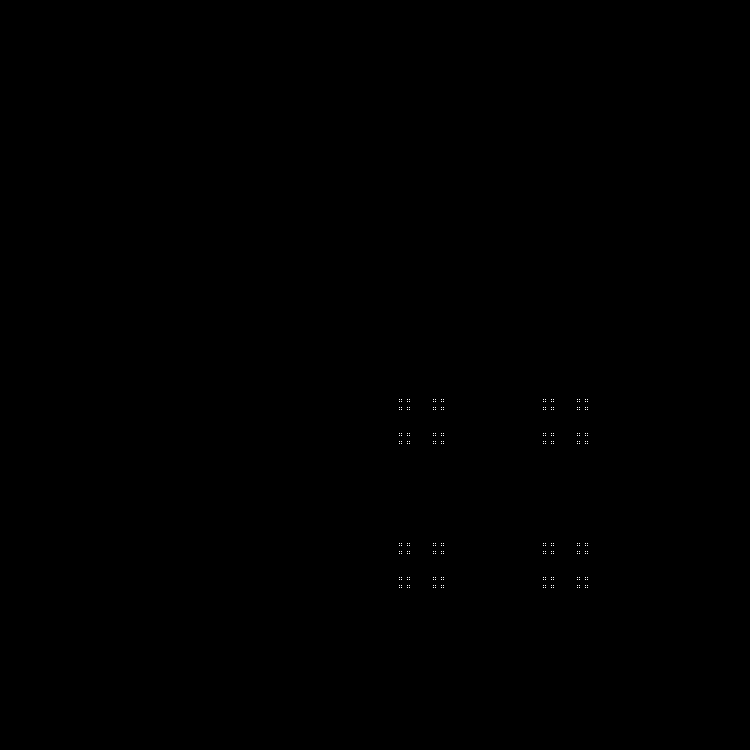
Еще одна последовательность в завершение:
Паттерн:

RGB:

Средний слой:

В динамике:
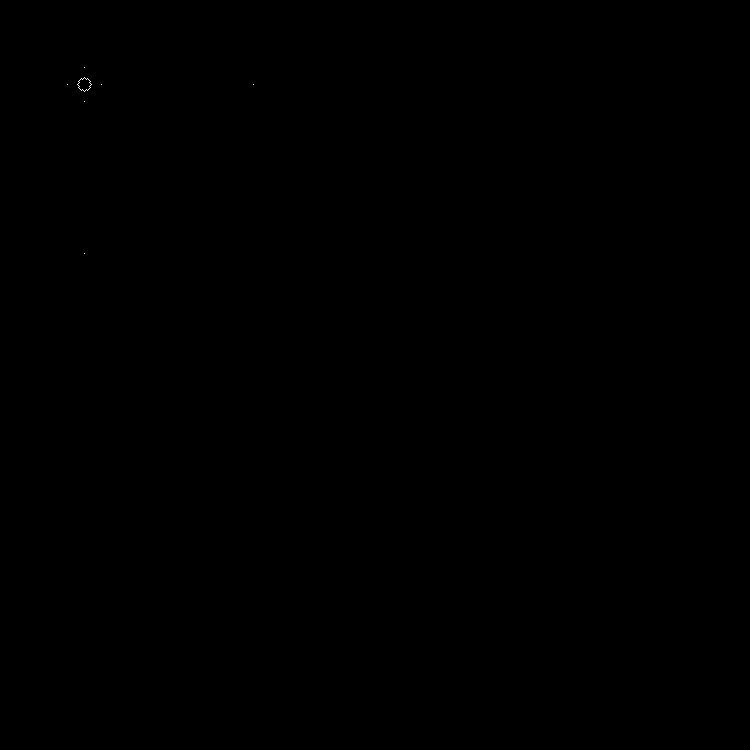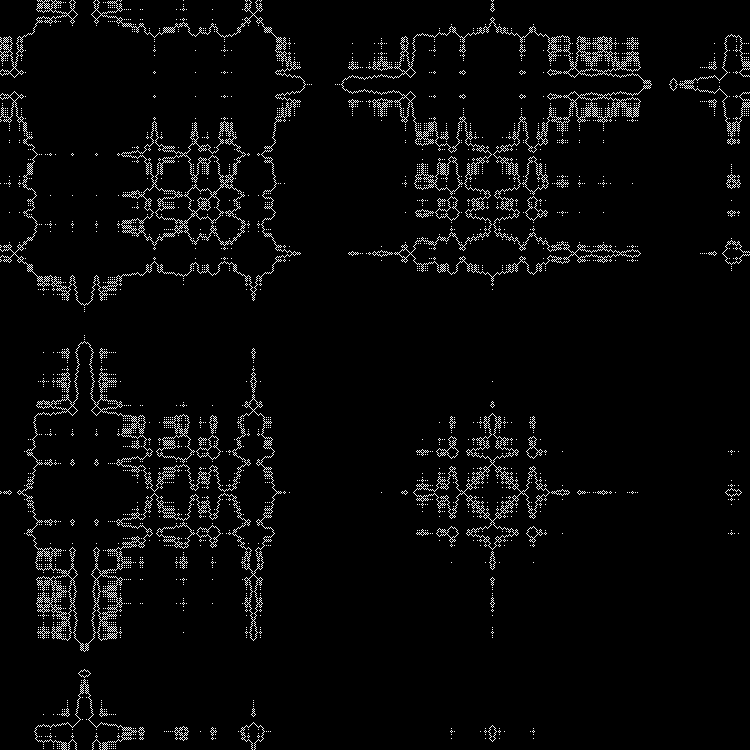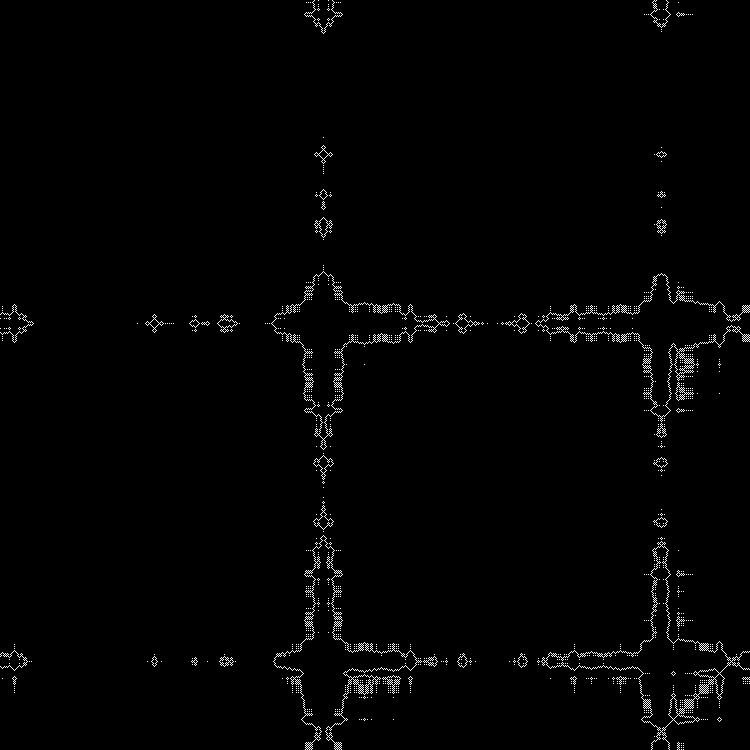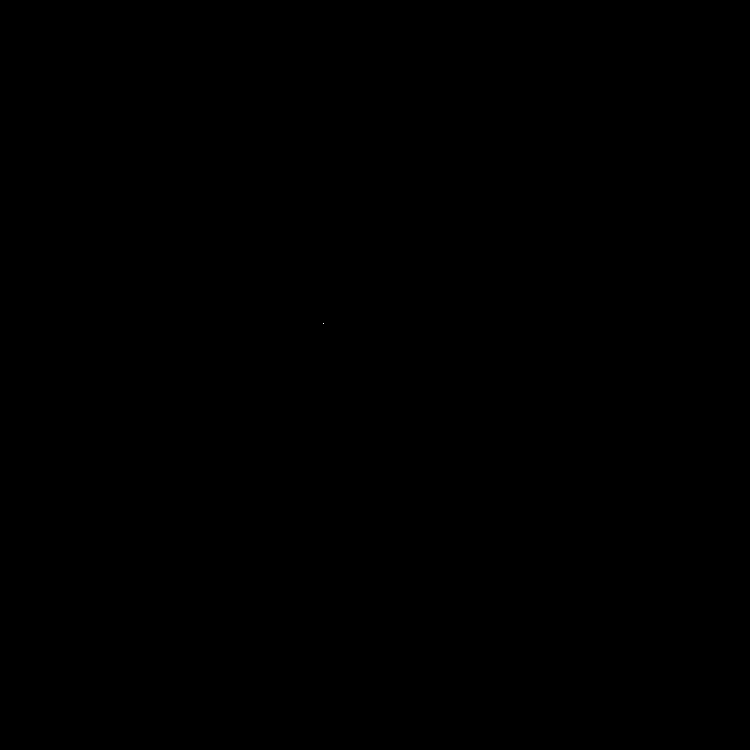
Другие квадратные корни можно вбить в скрипт. (Можно вбивать дробные значения).
Во втором скрипте можно вбить последовательность вручную.
Еще один скрипт для бильярдов. Координаты мышки — размеры бильярда. Паттерн в левой части формируется из последовательности, полученной с помощью остатков от деления (подробности в предыдущей статье). В правой части — четность