Ранее я показал элементарную реализацию алгоритма шинглов, позволяющую определять, являются ли два документа почти дубликатами или нет. В этот раз я поясню реализацию алгоритма, описанную Зеленковым Ю. Г. и Сегаловичем И.В. в публикации «Сравнительный анализ методов определения нечетких дубликатов для Web-документов».
Этим я начинаю серию из трех теоретических статей, в которых постараюсь доступным языком описать принцип алгоритмов шинглов, супершинглов и мегашинглов для сравнение веб-документов.
В публикации об алгоритмах поиска почти дубликатов предлагается версия алгоритма шинглов, использующая случайную выборку 84х случайных шинглов.
Почему именно 84? Использование 84х случайно выбранных значений контрольных сумм позволит легко модифицировать алгоритм до алгоритма супершинглов и мегашинглов, которые гораздо менее ресурсоемки. Их я опишу ближайшее время.
Рекомендую вооружиться ручкой и листком бумаги и фигурально представлять в виде рисунка каждый из этапов, описанных ниже.
Разберем, через какие этапы проходит текст, подвергшийся сравнению:
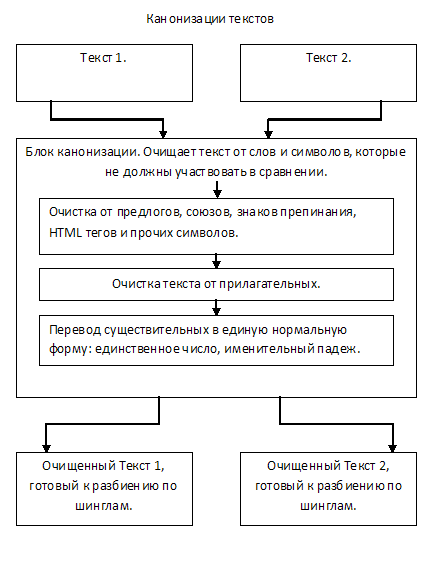
Что такое канонизация текста я описывал в своей прошлой статье об алгоритме шинглов. Но в коротко повторюсь. Канонизация текста приводит оригинальный текст к единой нормальной форме.
Текст очищается от предлогов, союзов, знаков препинания, HTML тегов, и прочего не нужного «мусора», который не должен участвовать в сравнении. В большинстве случаев так же предлагается удалять из текста прилагательные, так как они не несут смысловой нагрузки.
Так же на этапе канонизации текста можно приводить существительные к именительному падежу, единственному числу, либо оставлять от них только корни.
С канонизацию текста можно экспериментировать и экспериментировать, простор для действий тут широк.
На выходе имеем текст, очищенный от «мусора», и готовый для сравнения.
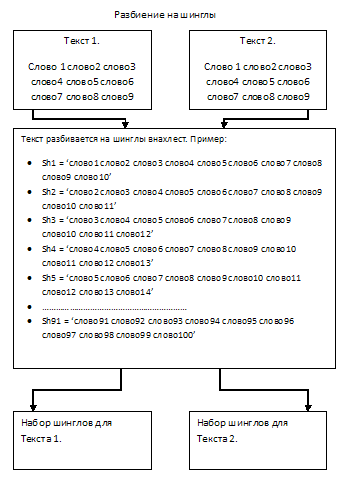
Шинглы (англ) — чешуйки, выделенные из статьи подпоследовательности слов.
Необходимо из сравниваемых текстов выделить подпоследовательности слов, идущих друг за другом по 10 штук (длина шингла). Выборка происходит внахлест, а не встык.
Таким образом, разбивая текст на подпоследовательности, мы получим набор шинглов в количестве равному количеству слов минус длина шингла плюс один (кол_во_слов — длина_шингла + 1).
Напоминаю, что действия по каждому из пунктов выполняются для каждого из сравниваемых текстов.
Вот этот этап самый интересный. Принцип алгоритма шинглов заключается в сравнении случайной выборки контрольных сумм шинглов (подпоследовательностей) двух текстов между собой.
Проблема алгоритма заключается в количестве сравнений, ведь это напрямую отражается на производительности. Увеличение количества шинглов для сравнения характеризуется экспоненциальным ростом операций, кто критически отразится на производительности.
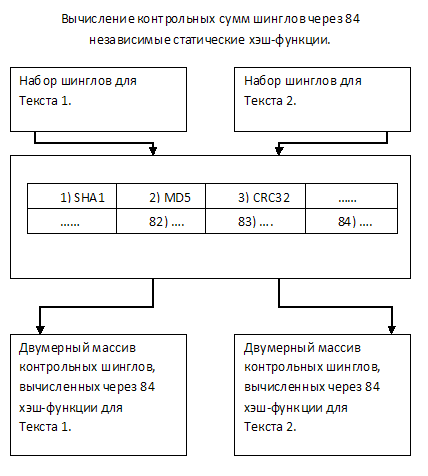
Предлагается представить текст в виде набора контрольных сумм, рассчитанных через 84х уникальные между собой статические хэш функции.
Поясню: для каждого шингла рассчитывается 84 значения контрольной суммы через разные функции (например SHA1, MD5, CRC32 и т.д., всего 84 функции). Итак каждый из текстов будет представлен, можно сказать, в виде двумерного массива из 84х строк, где каждая строка характеризует соответствующую из 84х функций контрольных сумм.
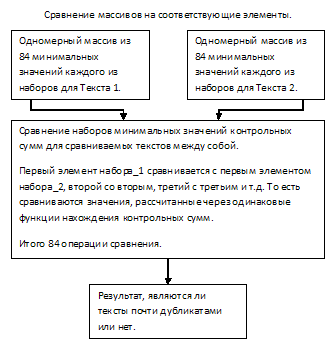
Из полученных наборов будут случайным образом отобраны 84 значения для каждого из текстов и сравнены между собой в соответствии функции контрольной суммы, через которую каждый из них был рассчитан. Таким образом, для сравнения будет необходимо выполнить всего 84 операции.
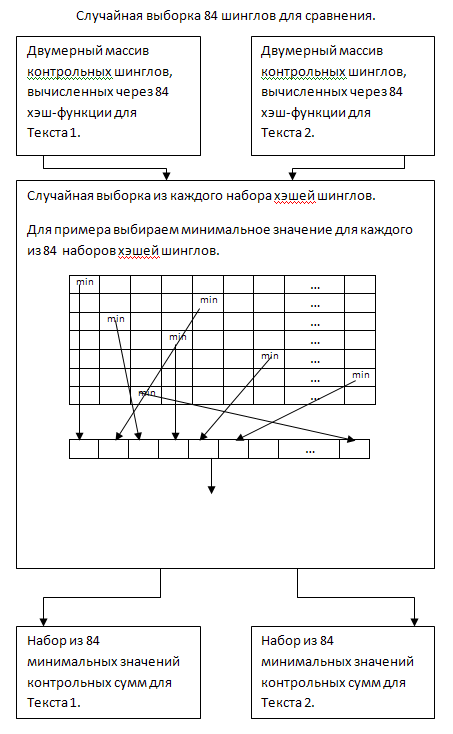
Как я описывал выше, сравнивать элементы каждого из 84х массивов между собой — ресурсоемко. Для увеличения производительности выполним случайную выборку контрольных сумм для каждой из 84х строк двумерного массива, для обоих текстов. Например, будем выбирать самое минимальное значение из каждой строки.
Итак, на выходе имеем набор из минимальных значений контрольных сумм шинглов для каждой из хэш функций.
И последний этап — сравнение. Сравниваем между собой 84 элемента первого массива с соответствующими 84ю элементами второго массива, считаем отношение одинаковых значений, из этого получаем результат.
Надеюсь, я доступно смог изложить теорию нахождения почти дубликатов для веб-документов, описанную в публикации Зеленкова Ю. Г. и Сегаловича И.В. не вдаваясь в особенности реализации на конкретном языке программирования.
Во второй статье цикла я собираюсь описать алгоритм супершинглов для веб-документов.
Надеюсь было интересно, удачи.
Оригинальная статья на нашем блоге: Часть 1. Алгоритм шинглов для веб-документов. Следите за обновлениями, скоро будет продолжение.
Этим я начинаю серию из трех теоретических статей, в которых постараюсь доступным языком описать принцип алгоритмов шинглов, супершинглов и мегашинглов для сравнение веб-документов.
В публикации об алгоритмах поиска почти дубликатов предлагается версия алгоритма шинглов, использующая случайную выборку 84х случайных шинглов.
Почему именно 84? Использование 84х случайно выбранных значений контрольных сумм позволит легко модифицировать алгоритм до алгоритма супершинглов и мегашинглов, которые гораздо менее ресурсоемки. Их я опишу ближайшее время.
Рекомендую вооружиться ручкой и листком бумаги и фигурально представлять в виде рисунка каждый из этапов, описанных ниже.
Итак, алгоритм шинглов для веб-документов
Разберем, через какие этапы проходит текст, подвергшийся сравнению:
- канонизация текста;
- разбиение на шинглы;
- вычисление хэшей шинглов с помощью 84х статических функций;
- случайная выборка 84 значений контрольных сумм;
- сравнение, определение результата.
1. Канонизация текста
Что такое канонизация текста я описывал в своей прошлой статье об алгоритме шинглов. Но в коротко повторюсь. Канонизация текста приводит оригинальный текст к единой нормальной форме.
Текст очищается от предлогов, союзов, знаков препинания, HTML тегов, и прочего не нужного «мусора», который не должен участвовать в сравнении. В большинстве случаев так же предлагается удалять из текста прилагательные, так как они не несут смысловой нагрузки.
Так же на этапе канонизации текста можно приводить существительные к именительному падежу, единственному числу, либо оставлять от них только корни.
С канонизацию текста можно экспериментировать и экспериментировать, простор для действий тут широк.
На выходе имеем текст, очищенный от «мусора», и готовый для сравнения.

2. Разбиение на шинглы
Шинглы (англ) — чешуйки, выделенные из статьи подпоследовательности слов.
Необходимо из сравниваемых текстов выделить подпоследовательности слов, идущих друг за другом по 10 штук (длина шингла). Выборка происходит внахлест, а не встык.
Таким образом, разбивая текст на подпоследовательности, мы получим набор шинглов в количестве равному количеству слов минус длина шингла плюс один (кол_во_слов — длина_шингла + 1).
Напоминаю, что действия по каждому из пунктов выполняются для каждого из сравниваемых текстов.

3. Вычисление хэшей шинглов с помощью 84х статических функций
Вот этот этап самый интересный. Принцип алгоритма шинглов заключается в сравнении случайной выборки контрольных сумм шинглов (подпоследовательностей) двух текстов между собой.
Проблема алгоритма заключается в количестве сравнений, ведь это напрямую отражается на производительности. Увеличение количества шинглов для сравнения характеризуется экспоненциальным ростом операций, кто критически отразится на производительности.
Предлагается представить текст в виде набора контрольных сумм, рассчитанных через 84х уникальные между собой статические хэш функции.
Поясню: для каждого шингла рассчитывается 84 значения контрольной суммы через разные функции (например SHA1, MD5, CRC32 и т.д., всего 84 функции). Итак каждый из текстов будет представлен, можно сказать, в виде двумерного массива из 84х строк, где каждая строка характеризует соответствующую из 84х функций контрольных сумм.
Из полученных наборов будут случайным образом отобраны 84 значения для каждого из текстов и сравнены между собой в соответствии функции контрольной суммы, через которую каждый из них был рассчитан. Таким образом, для сравнения будет необходимо выполнить всего 84 операции.

4. Случайная выборка 84 значений контрольных сумм
Как я описывал выше, сравнивать элементы каждого из 84х массивов между собой — ресурсоемко. Для увеличения производительности выполним случайную выборку контрольных сумм для каждой из 84х строк двумерного массива, для обоих текстов. Например, будем выбирать самое минимальное значение из каждой строки.
Итак, на выходе имеем набор из минимальных значений контрольных сумм шинглов для каждой из хэш функций.

5. Сравнение, определение результата
И последний этап — сравнение. Сравниваем между собой 84 элемента первого массива с соответствующими 84ю элементами второго массива, считаем отношение одинаковых значений, из этого получаем результат.

Заключение
Надеюсь, я доступно смог изложить теорию нахождения почти дубликатов для веб-документов, описанную в публикации Зеленкова Ю. Г. и Сегаловича И.В. не вдаваясь в особенности реализации на конкретном языке программирования.
Во второй статье цикла я собираюсь описать алгоритм супершинглов для веб-документов.
Надеюсь было интересно, удачи.
Оригинальная статья на нашем блоге: Часть 1. Алгоритм шинглов для веб-документов. Следите за обновлениями, скоро будет продолжение.