In this article, I will break down all the secrets of quantum computers piece by piece: what superposition (useless) and entanglement (interesting effect) are, whether they can replace classical computers (no) and whether they can crack RSA (no). At the same time, I will not mention the wave function and annoying Bob and Alice that you might have seen in other articles about quantum machines.
The first and most important thing to know is that quantum computers have nothing to do with conventional ones. Quantum computers are analog in nature, they have no binary operations. You have probably already heard about Qubits that they have a state of 0, 1 and 0-1 at the same time and with the help of this feature calculations are very fast: this is a delusion. A qubit is a magnet (usually an atom or an electron) suspended in space, and it can rotate on all three axes. In fact, the rotations of a magnet in space are the operations of a quantum computer. Why can it speed up calculations? It was very difficult to find the answer, but the most patient readers will find it at the end of the article.
Superposition
Before talking about the magical state 0-1 (superposition), let's first understand how the position of the magnet in 3D generally becomes zero and one. When creating a quantum computer, it can be decided that if the North (N) pole of the magnet (blue in the pictures below) looks up then this value is zero, if down then one. When a quantum program is launched, all qubits are set to zero (up) with the help of an external magnetic field. After the completion of the quantum program (a set of rotations of the qubits) it is necessary to obtain the final value of the qubits (to measure them), but how to do this? Qubits are extremely small and unstable. They are negatively affected by thermal radiation (therefore they are greatly cooled) and cosmic rays. You can't just look at a qubit and tell where its N pole is now. The measurement is performed indirectly. For example, you can bring magnets with N pole to the qubit from below and from above.

If the N pole of the qubit was directed upwards, then the qubit would fly down, and just this fall can be registered. After that, the state of the qubit is measured (Zero) and it is no longer physically suitable for further use in the quantum program. This is just an illustrative example, in each quantum computer the measurement is performed by its own methods, it is very difficult to find a description of how exactly, but the essence remains the same.
Now the most interesting, remember that our magnet can rotate in any direction, let's put it on its side? This is where all quantum algorithms start.

Great, we have put the qubit into a state of superposition, the famous "0-1 at the same time". When you try to measure such a qubit, it will fly up or down with the probability of about 50% (depending on the accuracy of building a quantum computer). As you can see, the state of the qubit is known exactly, we just rotated it 90o. Statements that it is at zero and one at the same time (or rushing between them) look strange, because only one sensor will be triggered during a measurement. Rotating another 90o takes the qubit out of the magical state.
Another important point: if the qubit is rotated from the vertical position not by 90o, but only by a couple of degrees, then during the measurement it will fly to "Sensor 0" with a very high probability, and in rare cases to "Sensor 1". This has been proven by experiments, I also tested it myself (IBM gives free access), a single atom behaves more complicated than an ordinary magnet.
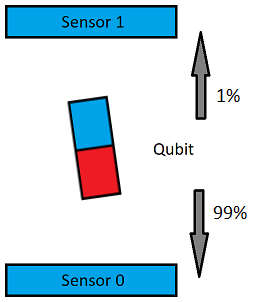
Any deviation from the vertical results in a probability of measuring one instead of zero. Accordingly, the initial initialization of qubits and all rotations of qubits must be done very accurately. It is also necessary to protect qubits from external influence very reliably, otherwise you will receive a calculation error. Modern quantum computers have extremely low accuracy, this is their big problem.
Now consider the very popular but misleading claim that superposition speeds up calculations. All quantum algorithms start by setting a group of qubits (register) into a superposition state (turning the magnets on their side). Starting from this moment, official science tells us that one qubit stores 0-1 at the same time, two qubits store 0-3 at the same time, eight qubits store 0-255, and so on. Any mathematical operation on this group of qubits will be performed immediately for all numbers stored by qubits.
Example: we have two groups of 32 qubits (two memory registers), we want to calculate the sum of numbers from these two registers. Performing addition once, we get absolutely all possible combinations of sums of numbers that can only be placed in these two registers. That is, about 18 quintillion addition operations were performed in one physical operation. It sounds very cool, but there is a catch.
After the completion of the quantum algorithm, we need to somehow pull out the result of the calculation. The problem is that a quantum computer won't give us all 18 quintillion results at once. After measurement, it will return only one of them, and that will be a random one. The measurement process destroys the qubits, which means that to get another result we will have to perform the operation again. To get all 18 quintillion results out of a quantum machine, you must run it at least 18 quintillion times.
What is with password cracking? Similarly, to convert the hash sum into a password you must run a quantum program very, very many times (as on a classical computer). Thus superposition (even if it is real) has no effect on the performance of the quantum machine by itself.
Entanglement
Quantum entanglement is the second whale on which the quantum computer is based. This is a curious effect that modern science cannot yet explain. But we will go a long way. Let's look at a typical piece of source code for a classical computer:
if (n > 50) then n = 50This line is difficult to execute on a quantum computer. After the operation (n>50), the qubits of the variable n will be immediately physically destroyed (because they had to be measured for the comparison operation), but we need this variable further in the code. Conditional jumps (and loops) are generally not available for quantum computers. How do they even survive then? One IF operation can still be performed, without taking a measurement: controlled NOT (CNOT), this is an analogue of the classical XOR operation. Two qubits participate in this operation, controlling and controlled:
if the N pole of the controlling qubit is pointing down (value 1), then the controlled qubit rotates 180 degrees
if the N pole of the controlling qubit is pointing up (value 0), then the controlled qubit does not change
This operation allows you to perform a trivial addition of integers for two qubit registers. To perform this operation, two qubits are briefly brought closer to each other, after which a series of separate rotations is performed. Measurements are not required, i.e., you can work with qubits further. After this operation the qubits are entangled. How does it show up? Let's start with the commonplace:

After we have entangled the qubits, they become dependent on each other. If the Q1 qubit has been measured as One, then the Q2 qubit will be measured as Zero. But this case is obvious and not interesting, let's put the qubits on their side before CNOT:
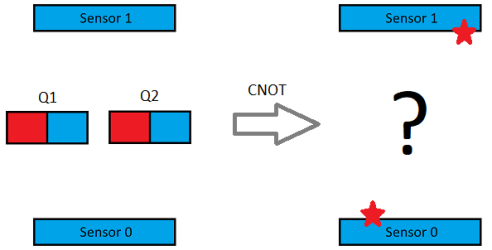
If the controlling qubit lies on its side, then the controlled one will either be rotated 180 degrees with a 50% probability or remain in the same state. The exact final position of the qubits in 3D space after such an operation is not known (they are allegedly in many states at once), because qubits cannot be viewed directly. But if entangled qubits are measured, then Q1 will randomly fly to sensor 0 or 1, and Q2 will always fly to the opposite sensor.
Why this happens no one knows. Logically, both qubits lie on their sides after the CNOT operation, which means that both should randomly fly on both sensors, without any dependence. In fact, there is a clear connection during the measurement (with some error, the system is analog). There are two theories on this:
Official science claims that qubits exchange information with each other (it is not known how, but instantly, more than the speed of light). When the first qubit is measured (hit on the sensor), it tells the second qubit exactly where it fell, and the second qubit remembers it and hits the opposite sensor during the measurement. This theory looks very strange, but here we must understand that official science adheres to the principle of superposition, that qubits are in the 0-1 state at the same time: when measuring the first qubit, the second can no longer remain in 0-1, it must urgently decide on the orientation.
The theory of hidden variables: it says that when interacting, qubits immediately agree on who will fall on which sensor. This happens due to a change in the physical parameter of the qubit, which is not yet known to science. This theory looks more logical, superluminal interactions are no longer required here. But this theory denies the existence of the superposition principle, which is the Holy Grail for modern science, so this theory is not being seriously studied.
In my opinion, the phenomenon of Entanglement itself is the main proof that Superposition does not exist. But I am not a theoretical physicist, so let's leave this topic. In the end, once official science ridiculed the theory of the movement of lithospheric plates, but in the end the guys figured everything out.
A couple final points about entanglement:
You can entangle many qubits, and this is a common thing for quantum computers. For this you need to run CNOT in turn for several qubits.
After the CNOT operation, the controlling qubit also changes its orientation in 3D space. Its N pole does not move up and down, but the qubit itself rotates around the Z axis, this phenomenon is called Phase Kickback. It is of great importance for quantum algorithms, this is what gives acceleration of calculations. We will talk about this below.
If, after entanglement, one of the qubits is transferred to the Zero state with the help of an external magnetic field (repeating the initial initialization), then this will not affect the second qubit in any way, the entanglement state will be broken. That is, the exchange of information at superluminal speed cannot be achieved using entanglement.
Entangled particles are sometimes compared to socks: I put one on my right foot, the second automatically becomes the left sock. This is an incorrect comparison. Entangled particles are more like two coins standing on their side: if one of them falls on heads, then the second will fall on tails, even if several hours have passed.
What Quantum Computers Cannot Do
Quantum computers are quite slow with a typical operating frequency of 100 MHz, but this is fixable. They are also quite small, 66 qubit machine is considered very good (you can store a couple of Int in memory), but this is also fixable. At the physical level, quantum computers do not (and may never) support:
conditional jumps and loops (I mentioned this earlier);
multiplication and division;
raising to a power and trigonometry.
All interaction between qubits is limited by the CNOT operation. But if quantum computers are so limited, why is there so much hype around them? When solving the problem head-on, there will be no superiority over classical computers, but there is a very short list of algorithms where a quantum computer can show itself. Let me remind you that each quantum operation is the rotation of one or two qubits, and one short-term pulse is enough to perform it. On the other hand, to simulate the rotation of a magnet on a classical computer, you need to calculate a lot of sines and cosines. Approximately on this feature effective quantum algorithms are built.
Shor's Algorithm
Shor's algorithm has long been a scare on the Internet, as it can theoretically crack RSA quite quickly. The hacking task itself comes down to finding two prime numbers that make up the RSA public key, i.e., we need to find two divisors for a very large number (about 512 bits for RSA-512). A simple enumeration on a classical or quantum computer will take a very long time, and as we saw above, the superposition principle does not help here.
In fact, there are two Shor Algorithms, classical and with quantum addition, let's start with the first one. Mathematicians have determined that the problem of simple enumeration can be replaced by the following equation:
a - the number 2 or 3 (in fact, any number, but 2 or 3 is exactly right, which one of them is impossible to say in advance);
N - the number for which we are looking for divisors (conditionally this is the RSA public key);
mod is an operation that returns the remainder of an integer division;
x is an auxiliary number, having found it (by simple enumeration) we will quickly find the divisors of the number N. The desired x must be greater than zero, even and the minimum of all possible.
Mathematicians have determined that the number of steps to enumerate the number x will be significantly less than a simple enumeration of the numbers a and b using the formula a*b=N. I checked how it works, ran the formulas in Excel and found the divisors for the number 15: it is enough to iterate over just two numbers x, ignoring 0 and all odd ones.

This effect should be more pronounced for larger numbers, but there is a catch. An experienced eye, of course, noticed the exponentiation operation, as well as the search for the remainder of the division. There may be fewer enumeration steps, but each step itself has become very complex, and their complexity will grow exponentially for large numbers N. Also, you are probably wondering, what does quantum computers have to do with it, if everything worked out in Excel?
Quantum Shor’s Algorithm
Shor's quantum algorithm also starts by calculating the formula axmod(N), but there are a lot of problems here:
raising to the power, multiplication and division (including integer division with remainder) are not supported at the hardware level;
the number of qubits is very limited, it is problematic to keep the result ax in memory;
loops are not supported, which means that iterating over the number x must be done without them.
The guys did not despair and came up with a set of workarounds. The number x at the input of the quantum program is given as qubits in superposition. The formula axmod(N) will supposedly be calculated immediately for all possible numbers x in one operation, but as we saw above, this is useless, because we can measure only one result of all, and it will be for random x.
Further, the formula axmod(N) itself is replaced by a very strange code (a simulation of a quantum computer is shown):
X = Register('X', 8)
F = Register('F', 4)
X.H()
F[3].X()
for i in range(8):
for j in range(2**i):
Fredkin(X[i], F[0], F[1])
Fredkin(X[i], F[1], F[2])
Fredkin(X[i], F[2], F[3])Register is a function that initializes the specified number of qubits (8 and 4), it returns the register of qubits with the value 0x0 (all N poles are directed upwards);
method H is Hadamard gate, puts qubits on their side (sets to superposition);
method X rotates a qubit by 180o (like binary NOT);
Fredkin function is standard for quantum computing, it swaps the values of two qubits if the first parameter (controlling) is set to one (N pole is directed downwards). The function consists of 8 CNOT operations and 9 single qubit rotations;
register X stores the number x;
register F stores the result of axmod(N)
The source code is available in my repository.
You are probably very surprised how this can even work? This is a workaround that allows to calculate the formula axmod(N) for a=2, N=15 and any x. There are several methods that allow to create a set of qubit rotations for any numbers a and N. I have no idea how it works, the documentation for quantum algorithms has low quality, but my own tests have confirmed that the calculations are correct.
Accordingly, if we want to crack some RSA-512 key, then first for this particular key we must create a scheme that will include a lot of rotations. But how many times should we run such the scheme? Did you notice the two nested loops in the source code above? For the number N=15, the circuit is launched 255 times, for N=21 - 511 times, for N=35, which is still unattainable by quantum computers, there will be 2047 launches. The number of operations increases dramatically.
Quantum Phase Estimation
Congratulations to all the most patient readers, having gone a long way of misunderstanding, we got to the very essence of quantum computers. When we calculate the formula F= axmod(N) on a classical computer, we wait for the value F=1. But when we work on a quantum machine, it doesn’t really matter to us what is ultimately stored in the register F, the solution to the problem will be stored in the input register X.
In the classical computer XOR operator (CNOT analogue) does not change the value of the controlling variable. But let me remind you that when we perform CNOT operation in the quantum machine, it changes both qubits:
the N pole of the controlled qubit moves up and down, depending on the state of the controlling one;
the N pole of the controlling qubit does not move up and down, but the qubit itself rotates along the Z axis.

The deviation of the qubit along the Z axis is called the phase. During the execution of a quantum program, all qubits accumulate some phase change. Mathematicians have proven that by measuring the final phase of all qubits in the input register X, it is possible with a very high probability to find the divisors of the number N (to hack RSA), even if the result in the register F is not 1. RSA-512 requires only about 2000 runs of the algorithm on a quantum computer. But there is a catch. Even two.
The first problem is that one must somehow be able to measure the phase. For this, the QFE (Quantum Phase Estimation) algorithm is used, which requires additional rotations of qubits by very small angles. For N=15 you need to rotate the qubits by 1.4o, for N=35 the rotations will be 0.175o. For RSA-512 you need to rotate the qubit by insignificant 180/21022 degrees and doing this 1022 times. Qubits are an analog system, if you make a mistake with the angle then you will get an error at the output. Modern quantum computers cannot cope with the number N=35, they already lack the accuracy of rotations. But this is not the biggest problem, the most insignificant turns can be simply neglected, almost without losing the accuracy of the entire algorithm.
The second problem is the calculation of axmod(N). For RSA-512 it only needs to be calculated 2000 times. But look again at the two nested loops: one such calculation is more than 21022 consecutive rotations of qubits. This is nonsense. Quantum computers are not capable to hack RSA, even if they grow to a million qubits. There are scientific articles about how they managed to optimize this part and make it hundreds and thousands of times faster, but they always keep silent about exactly how many operations are required when N is about 2511.
Quantum Computer Simulators
Quantum computer simulators are much slower than their real counterparts. This happens because simulators do their job honestly. When you create a register of 8 qubits in the simulator, all possible values for these qubits are stored in memory (an array of 256 values is created). If you create two registers of 8 qubits each and perform the A+B operation, the simulator will calculate and store in memory all possible combinations of additions (it will create an array of 65536 values). This will be significantly longer than a single addition operation, but after that the simulator can return all these values to you without destroying the data on each "measurement". To get all the results on a real quantum computer, you will run it at least 65536 times (the result is returned randomly, there may be repetitions), and in general, it will take even longer than on the simulator.
But if qubits are just magnets in 3D space, is it possible to create a simulator that rotates them in virtual reality? I tried and created the FastQubit library. Most of the operations work successfully (even Bell states), and such a simulator has a significant advantage over the real quantum computer:
there can be millions of qubits and they are completely stable, no errors;
qubits can be viewed at any time, the exact position in 3D can be determined, without destroying them.
But there is a catch. Phase Kickback doesn't work correctly in my library:
Q[0].H()
Q[1].X()
Q[0].P_pi(8)
Q[1].P_pi(8)
CNOT(Q[0], Q[1])
Q[1].P_pi(-8)
CNOT(Q[0], Q[1])This chain of operations should eventually shift the Q[0] qubit phase by 45o, but in my case, the shift is performed by 90o. The fact is that the exact position of qubits in 3D after the first CNOT operation is not known to science (but he is known after the second CNOT). Here they usually mention superposition, that qubits are in many states at once. I used the documentation for quantum operations and made the turns exactly as they are described there. But no, in fact no one knows what turns are performed.
If you get this short code to work correctly, you may be eligible for a Nobel Prize. But don't try to use a workaround: of course, you can turn the phase to the desired angle under certain conditions, but this will stop working when entanglement between several qubits is added to the quantum program.
Conclusion
The documentation for quantum computers is as pretentious as possible, even elementary things turn into complex formulas. I have spent weeks trying to figure out what is really hidden in them. Articles in the news and blogs, on the contrary, are extremely superficial, philosophical, and very often contain false information. No one ever publishes the number of how many operations are required to hack RSA-512 (and it is not the most crypto-resistant). Instead, you will be shown several formulas for calculating the complexity of the algorithm, making it as incomprehensible as possible.
I am not calling for an immediate end to all funding for quantum computing research. This is fundamental research that can bring unexpected useful results in other areas. But it is necessary to stop publishing scary stories about the post-quantum era.