Пролог
В продолжение опубликованной на выходных статьи.Компиляторы — пожалуй одна из самых интересных тем системного программирования.
Эта статья не расскажет как написать идеальный, или, хотя бы, работающий компилятор, но она поможет прояснить пару аспектов его работы, при помощи метода топологической сортировки сети.
Что такое сети?
Сеть — это бесконтурный ориентированный граф (В предыдущей статье разбирался вопрос контуров и методы их нахождения).Для алгоритма нам понадобятся некоторые свойства, часть из них была более подробно разобрана в самой первой статье.

Как видно из картинки, каждую вершину можно охарактеризовать числом дуг, входящих в неё (полустепень захода), и числом дуг, исходящих из неё к другим вершинам (полустепень исхода).
Если у вершины нет ни одной входящей дуги, вершина называется источником сети.
Если у вершины нет ни одной исходящей дуги, вершина называется стоком сети.

Рассмотрим сеть на примере сборки приложения.
Файлы обозначим вершинами.
Роль дуг в сети проще понять по картинке:
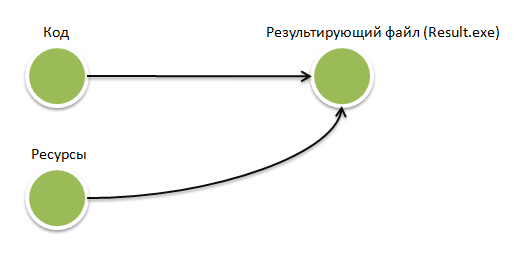
Дуга, идущая из вершины «Код» в вершину «Результирующий файл» говорит о том, что «Код» должен быть обработан прежде, чем будет получен Result.exe
Перед тем, как вершина может быть обработана, следует обработать все вершины, ссылающиеся на неё.
Всё кажется простым, когда мы видим нарисованную сеть небольшого размера.
Давайте перейдем поближе к реальности и рассмотрим построение небольшой программы.
Пример 1:

К сожалению, даже современные компиляторы не такие глазастые, чтобы увидеть здесь правильную последовательность сборки.
Алгоритм
Как же тогда компилятор понимает, что ему сделать сначала, а что потом?Сначала опишем, что же мы хотим от нашего алгоритма, а потом приведем код.
Итак, наша цель — создать сеть, состоящую из нескольких уровней.

Из рисунка видно, что задачи внутри одного уровня зависят только от задач на младших уровнях, и независимы друг от друга.
В таком случае, для достижения цели нам сначала надо в любом порядке выполнить все задачи уровня 0, потом, в любом порядке, задачи уровня 1, и т.д., до уровня 3 (последнего).
Для решения задачи, нам понадобится представление графа в виде матрицы (ij элемент = 1, если есть дуга из вершины i в вершину j, и равен 0, если дуги нет).
Рассмотрим ещё один пример
Пример 2:

В строке под таблицей даны полустепени захода для всех вершин. Каждое число отражает сумму единичек в соответствующем столбце матрицы.
На первом шаге алгоритма мы выбираем все вершины с нулевой полустепенью захода, заносим их в нулевой уровень и, мысленно, выкидываем из графа.
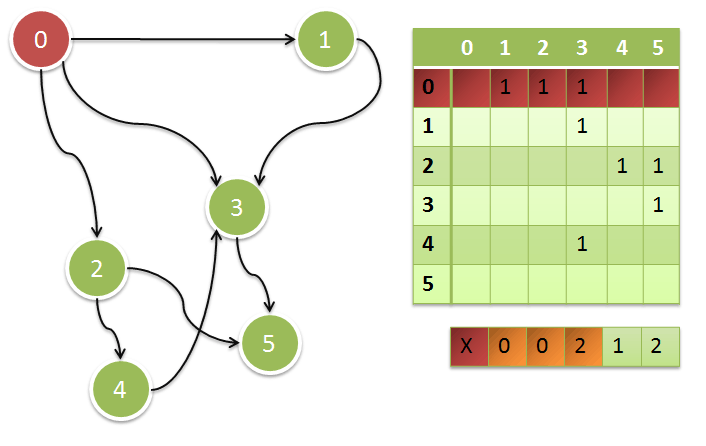
В результате, (мы больше не учитываем строки матрицы, соответствующие обработанным вершинам) полустепени захода остальных вершин уменьшатся.
Далее, проделываем тоже самое с оставшимися вершинами, имеющими нулевую полустепень захода и помещаем их в первый уровень:

Последующие шаги выполняются аналогично

В самом начале мы потребовали, чтобы наш граф был бесконтурным, благодаря этому требованию на каждом шаге у нас будут появляться новые вершины с нулевой полустепенью захода.
Применим алгоритм к нашей сети из примера 1:

Пример реализации
Базовый каркас, который нам понадобится:public class GraphNode
{
public List<GraphNode> LinkedNodes;
}
public class Graph
{
public List<GraphNode> nodes;
public void TopologicSort(out List<string> algResult, bool animated)
}
* This source code was highlighted with Source Code Highlighter.Вспомогательная функция, возвращающая массив полустепеней захода для всех вершин сети.
int?[] GetInputNodesArray()
{
int?[] array = new int?[this.nodes.Count];
for (int i = 0; i < this.nodes.Count; i++)
{
array[i] = this.nodes[i].LinkedDownNodes.Count;
}
return array;
}
* This source code was highlighted with Source Code Highlighter.И, наконец, алгоритм:
public void TopologicSort()
{
List<List<GraphNode>> levels = new List<List<GraphNode>>();
int?[] workArray = GetInputNodesArray();
int completedCounter = 0;
int currentLevel = 0;
bool pathFound;
while (completedCounter != this.nodes.Count)
{
levels.Add(new List<GraphNode>());
// Во избежание обработки вершин, с нулевой
// степенью захода, возникших по ходу следующего цикла,
// помечаем их заранее.
for (int i = 0; i < this.nodes.Count; i++)
{
if (workArray[i] == 0)
{
workArray[i] = null;
}
}
for (int i = 0; i < this.nodes.Count; i++)
{
if (workArray[i] == null)
{
// Если вершину следует обработать, помещаем её
// В соответствующий ей уровень и корректируем
// Массив степеней захода остальных вершин
levels[currentLevel].Add(this.nodes[i]);
this.nodes[i].Tag = currentLevel; // Оставляем в вершине метку о её уровне
foreach (GraphNode node in this.nodes[i].LinkedNodes)
{
int linkedNode = this.nodes.IndexOf(node);
workArray[linkedNode]--;
}
workArray[i] = -1; // Помечаем вершину как обработанную
completedCounter++;
}
}
currentLevel++;
}
}
* This source code was highlighted with Source Code Highlighter.Эпилог
Компиляторами не ограничивается применение данного алгоритма, он также может быть применен например, при программировании нейронных сетей, или планировании крупных проектов.В следующий раз будет рассказ про алгоритмы поиска кратчайшего пути на графе (алгоритм Дейкстры и алгоритм Волнового фронта).
Исходники
Программа и Исходники на C#: СкачатьПо данной ссылке много более функциональная программа и несколько примеров сетей для сортировки.
Презентация с опущенными шагами алгоритма: Скачать