On the Internet and in non-fiction literature, you can often find various mathematical tricks: you are asked to think of a number, then perform a series of arithmetic operations with it. After that, the conversation partner accurately guesses the number you got. Most of these tricks are based on the fact that the original number is insensibly replaced by another during transformations, and then reduced to a known answer in several steps. Such tricks, for example, can be found in the books of Yakov Perelman.
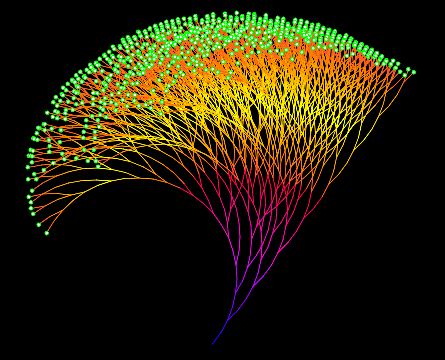
The Collatz conjecture leaves all such tricks behind. At first glance, it may seem that this is also some kind of trick with a catch. However, upon closer examination, it turns out that there is no catch. You think of a number and repeat one of two arithmetic operations for it several times. Surprisingly, the result of these actions will always be the same. Or, may be not always? Nobody knows for sure, but so far no one has been able to get something else.
Let's try. So, think of any positive integer. Then follow a simple algorithm:
If the number is even, divide it by 2.
Otherwise, multiply it by 3 and add 1.Repeat step 1 with the resulting number.
What do you think we will get as a result if we repeat steps 1 and 2 many times?
The German mathematician Lothar Kollatz believes that for any positive integer, sooner or later we will first get 4, then naturally: 2, and then 1. And after that we will walk in a circle, again and again getting the chain 4-2-1. The most amazing thing is that we will come to such result, no matter what number we start with.

Hard to believe? This is not difficult to verify, especially since the conditions of the problem are very simple. Perhaps, at the moment, this is the simplest formulation of an unsolved mathematical problem—everyone can multiply and add. To be fair, it is worth noting that for some initial numbers it will take a long time to count. So for guessing in a company of friends this “trick” is only suitable for small initial numbers.
But we can always write a little program—could not be easier: a loop with one condition. Here is my version of the program in Python:
import random
def calc(n):
while n>1:
if n%2==0:
n = n//2
else:
n = 3*n+1
yield n
n = random.randint (1,1000)
steps = [n]+[n for n in calc(n)]
print (steps)
print ('Number: {}. Steps: {}. Maximum: {}.'.format(steps[0],len(steps),max(steps)))Feel free to experiment with this hypothesis yourself. By the way, you can find many interesting visualizations on the web showing the distribution of solutions and steps for different initial data. And there is also a site that contains options for implementing this task for many programming languages.
Do you know what else is interesting? Collatz's statement is not called a hypothesis for nothing—so far no one has been able to come up with its logical proof. Lothar Kollatz formulated his hypothesis back in the 30s of the 20th century, and since then numerous attempts have been made to prove or disprove this statement using strict mathematical logic. But all that mathematicians have been able to achieve is simply to test the hypothesis experimentally. In this problem, the program search for a solution is essentially not limited by anything, except for computing power. While the hypothesis has not been refuted—even for huge initial numbers, sooner or later the algorithm reaches 1. To solve this problem, a project of voluntary distributed computing was even organized. But this is not enough for classical mathematics. Numbers are sometimes very tricky. Somewhere among the incredibly huge initial numbers, there may be such an initial number for which the hypothesis is not confirmed.
By the way, the Collatz conjecture has several less famous names:
the 3n+1 problem is a variant of the step for odd numbers;
hailstone hypothesis—sequence graphs are somewhat reminiscent of hail trajectories in the atmosphere;
the Ulam conjecture, named after the Polish mathematician Stanisław Ulam;
the Kakutani problem, named after the Japanese mathematician Shizuo Kakutani;
the Thwaites conjecture, named after the English mathematician Brian Thwaites;
the Hasse algorithm—named after the German mathematician Helmut Hasse;
the Syracuse problem.
Judging by the amount of different names, it is clear that mathematicians are seriously interested in this problem. However, it turned out that this is one of those "tough" tasks that are very easy to formulate, but extremely difficult to solve. Just like Fermat's Last Theorem.
The numbers in this problem behave very odd: in some cases, the calculations reach 1 very quickly, and sometimes the subtotal gets to a fairly large number, and then quickly “breaks” down to the very unit. For example, for the initial number 27, the subtotal reaches 9232, and then quickly descends to 1 in a few steps. As a result, the number of steps for 27 is 111. And this despite the fact that for 26 it is 10 (the maximum intermediate number is 40), and for 28: 18 (the maximum intermediate number is 52).
Although mathematicians have not been able to fully logically confirm or disprove the hypothesis, they still achieved something. As is often the case, scientists approach the solution gradually. More recently, on September 8, 2019, University of California mathematician Terence Tao published a proof showing that the Collatz conjecture is at least “almost” true for “almost” all numbers. The story of how mathematicians stormed this problem and what Terence Tao managed to achieve is described in details here.
Variety of the proof of the Collatz conjecture have repeatedly appeared in journals and on the net. However, unfortunately, all of them either contained errors or were incomplete. So the hypothesis is still just the hypothesis, and also the really cool and beautiful mathematical trick.
This is a translation of my original article.