There are about 14,000 species of ants on Earth, each of them has its own name. However, no matter how hard you try, you will not find Langton's ant in any biological encyclopedia.
The thing is, Langton's ant is just a mathematical abstraction, a model for describing the behavior of a dynamic system. Sometimes it seems that mathematicians are really fascinated with ants—just to mention, the ant colony optimization algorithm that has already become a classic. Also, ants are quite common in all sorts of logical models and math problems.

From chaos to strict order
Let's take a closer look at our Langton's ant. He lives on an endless field of white cells. He has two inexhaustible buckets—one with white paint, the other with black. The ant moves along the cells of the field from one cell to another. In the meanwhile, he executes a simple algorithm:
If the cell is white, the ant repaints it black, turns 90° to the right (clockwise) and takes a step forward.
If the cell is black, the ant repaints it white, turns 90° to the left (counterclockwise) and takes a step forward.
Basicly, this is it. The life of Langton's Ant seems quite sad, but, as we'll soon discover, he is not ready to put up with such an outrageous situation and is trying his best to escape.

Writing a program that simulates the behavior of Langton's ant is a simple task. There are many examples of the implementation of this algorithm on the Internet: easy and more complicated—with a set of additional settings.
Try to observe the movements of this ant along its checkered field. At first glance, his steps are completely chaotic—there is no order. But, to paraphrase a famous saying, if you are looking at the ant for a long time, you can see him running away. Somewhere after 10,000 steps, the ant suddenly realizes the pointlessness of existence and makes an attempt to escape—he begins to build a periodic structure. Every 104 steps he is moved into two cells diagonally. After that, the steps are repeated. The behavior of the ant will never become chaotic—now it will continue to move along a wide diagonal strip-highway, consisting of black and white cells.
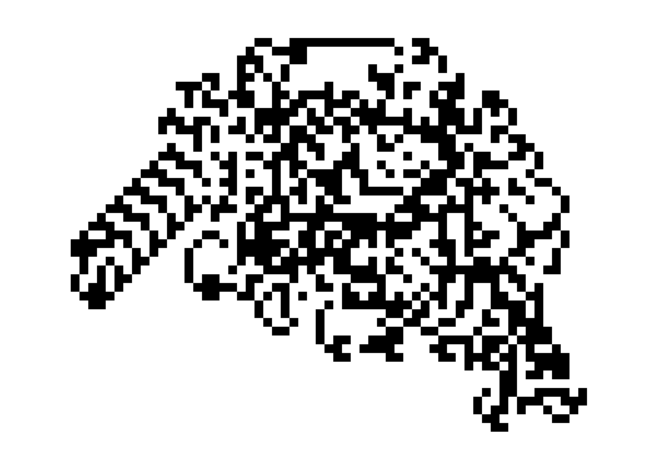
Already this sudden change in the behavior of Langton's ant makes one wonder how a strict order is suddenly born from a completely chaotic system?! But our ant has an even more impressive feature. What would happen if, before the ant begins to move, a finite number of some of the cells adjacent to the starting point are painted black? Could it change the behavior of the ant?
Ian Stewart's book, The Great Mathematical Problems, gives a fascinating description of this experiment: "We can choose any cells for this: it can be a random set, a black square, or Mona Lisa. There may be a million, or a billion, or even more, but not an infinite number".
What will happen in the end? In all the experiments, the ant, wandering through the cells, sooner or later again began to build its highway using the same 104 steps. It seems that the ant has a complex self-learning algorithm, which eventually leads it to a regular repeating pattern of steps. In fact, the algorithm is still the same—the two rules described at the beginning of the article. But the most interesting thing about this whole model is that mathematicians still do not know the answer to the following questions:
Does the ant always start the orderly movement?
If the answer to the previous question is yes, then is the highway of 104 steps repeated the only construction ("attractor") that the ant eventually begins to build?
The only thing that mathematicians can say with certainty is that regardless of the initial configuration of the cells, a freedom-loving ant will not remain forever in a closed area. American scientist Christopher Langton invented his ant back in 1986. Since then, no one has been able to explain the strange behavior of this mysterious model.
Langton's ant modifications
Langton's ant is essentially a cellular automaton, a regular grid in which, at each step, the color of cells changes according to a certain set of rules, usually depending on the color of neighboring cells. The most famous cellular automaton is John Conway's Game of Life. Scientists have come up with a wide variety of cellular automata, but perhaps none of them can be compared in mystery with our ant.
By the way, like the other cellular automata, Langton's ant has its modifications. For example, sometimes our ant is loaded with buckets of additional paints. In this case, separate rotation rules are set for each color. You can also add other ants to the ant (each with a bucket of its own color) and see how they interact. There are also variants with a hexagonal grid that uses six different rotation options: no change, 180°, 60° right, 60° left, 120° right and 120° left.

You can also change the behavior of each ant in the system. To do this, they came up with a way to encode the algorithm as a string of characters R—turn right and L—turn left. In this entry, each position corresponds to the color of the cell to which the ant came. For the classic Langton's ant, the notation would be: RL. Also, sometimes two more commands are added: C—continue moving in the same direction (sometimes the letter F is used), U—turn around 180° (sometimes the letter B is used). Ants with modified behavioral algorithms begin to behave in a completely different way—they no longer always build highways. Many of them immediately begin to make symmetrical patterns. This is how, for example, ants behave with repeating pairs: LL and RR. For example, LRR.

You can use one of the ready-made programs or program this wonderful and mysterious system yourself and experiment with various options for its implementation. For ants, you can come up with new algorithms, change their number, the initial direction of movement, and the starting points on the plane. You can also experiment with the initial coloring of some cells on the plane. For example, a freedom-loving ant with the RL rule can successfully get out of a closed square.

For this cellular automaton, you can come up with many modifications with different behavior, but the classic Langton's ant remains one of the unsolved problems of mathematics so far. I have always been amazed by such systems with their simplest formulations and inexplicable behavior. They remind us of how much we still do not know about the mathematical laws of our world. Perhaps the solution of such problems in the future will lead us to understand something more than the behavior of the simplest cellular automaton.
This is a translation of my original article.