7.4 Точность по возмущающему воздействию
Рассмотрим замкнутую САР, на которую может воздействовать возмущающее входное воздействие .
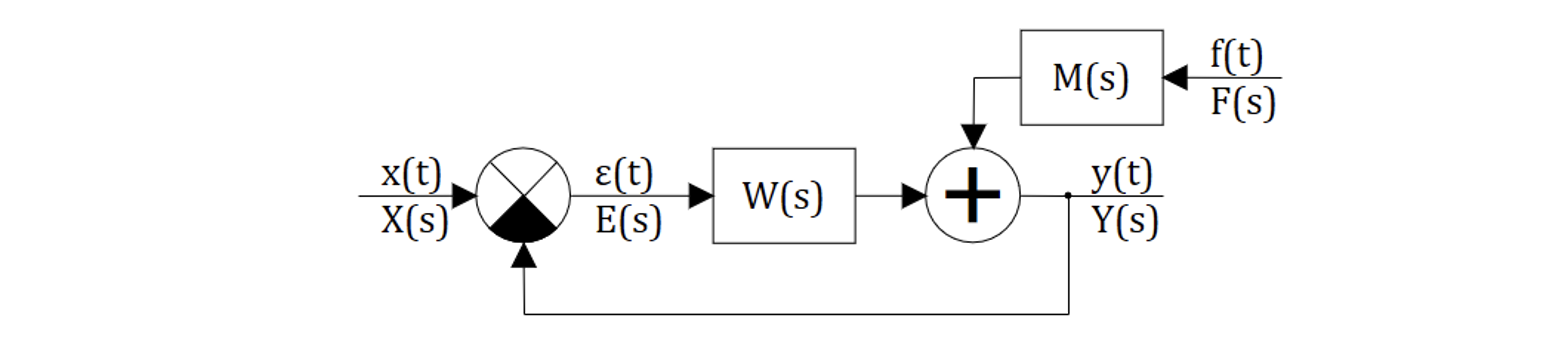
Предположим, что , т.е. управляющее воздействие отсутствует. В этом случае САР обязана поддерживать на выходе
(с некоторой степенью точности)
В этом случае , поэтому установившуюся ошибку
можно вычислить как:
Используя передаточную функцию замкнутой САР по возмущающему воздействию , имеем:
7.4.1 Ступенчатое возмущающее воздействие
Пусть ступенчатое возмущение
Передаточная функция равна:
Анализ соотношения (7.4.3) показывает, что:
- если САР – статическая (т.е. полином имеет свободный член, равный 1), то:
- если САР – астатическая (степень астатизьма ), то:
Графическая иллюстрация переходного процесса:
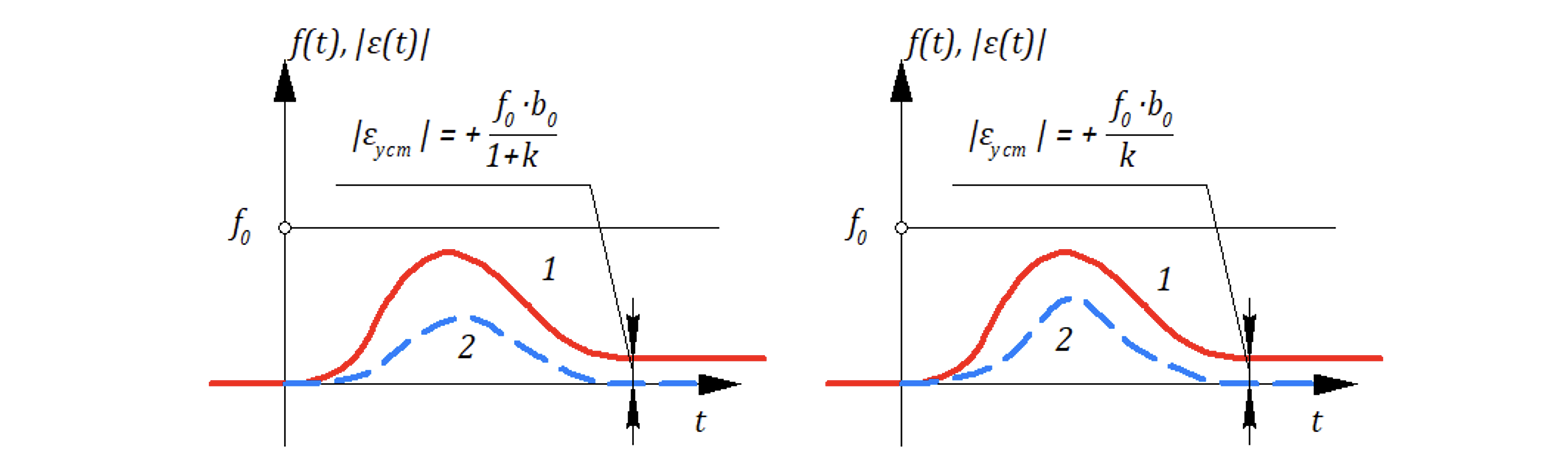
Кривые 1 на рисунках соответствуют случаям, когда полином имеет свободный член, равный
(причем для данных рисунков
), а кривые 2 соответствуют случаям, когда полином
не имеет свободного члена.
Случай, когда полином не имеет свободного члена принято называть астатизмом по возмущающему воздействию.
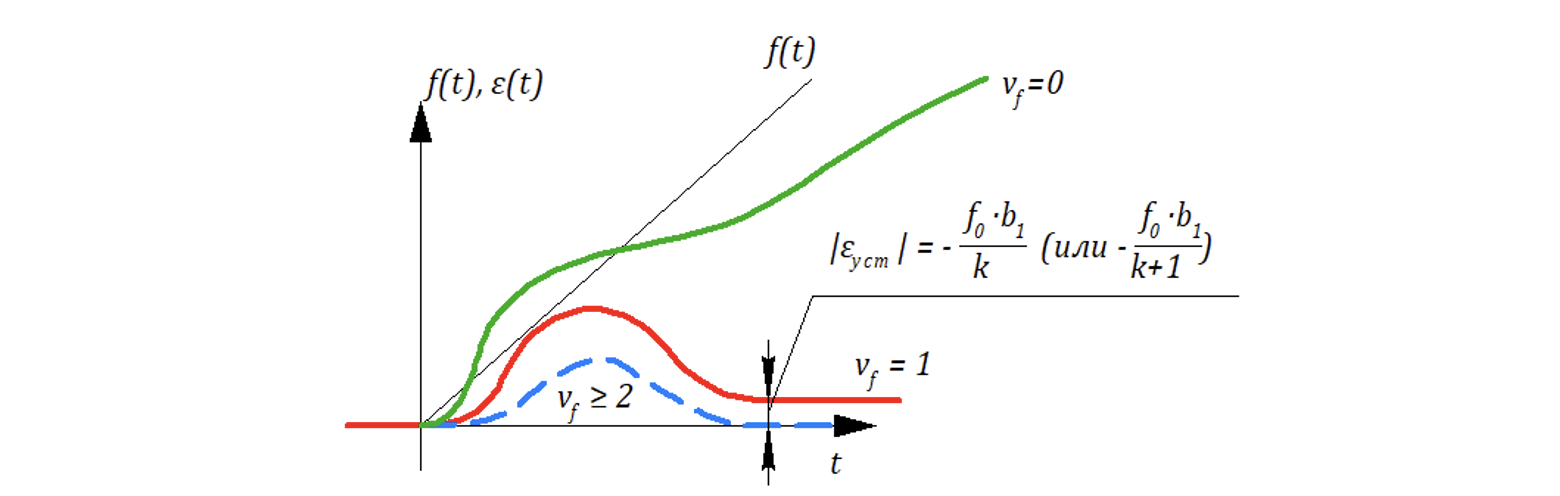
7.4.2 Линейное возмущающее воздействие
Пусть возмущающее воздействие перейдем в изображение
Подстановка в формулу (7.4.2) показывает, что если САР не имеет астатизм по возмущающему воздействию, то:
Если САР имеет астатизма по возмущающему воздействию , то
.
В завершении обсуждения рассмотренных подразделов сделаем некоторые заключающие выводы:
Система автоматического регулирования называется астатической по управляющему воздействию, если при воздействии, стремящемся к установившемуся значению ошибка (рассогласование) стремится к нулю независимо от величины управляющего воздействия.
Система автоматического регулирования называется астатической по возмущающему воздействию, если при его приложении ошибка (рассогласование) стремится к некоторому установившемуся значению, зависящему от величины установившегося значения возмущающего воздействия.
Хорошей практикой при проектировании САР является придание ей свойства астатизма как по управляющему воздействию , так и по возмущающему воздействию
.
Анализ подраздела (7.3) показывает, что астатизм по управляющему воздействию обеспечивается за счет астатических регуляторов (структура которого содержит интегрирующие звенья) – например ПИ-регуляторов.
Наряду со статическими и астатическими САР различают статические и астатические регуляторы.
Статический регулятор при ступенчатом управляющем воздействии на его входе обеспечивает на выходе (регулятора) асимптотически-устанавливающиеся значения.
У астатических регуляторов при ступенчатом входном сигнале выходной сигнал (регулятора) линейно (или нелинейно) нарастает без ограничений по уровню.
Пример
Определить установившиеся ошибки по управляющему и возмущающему воздействиям, если и
для следующей САР:
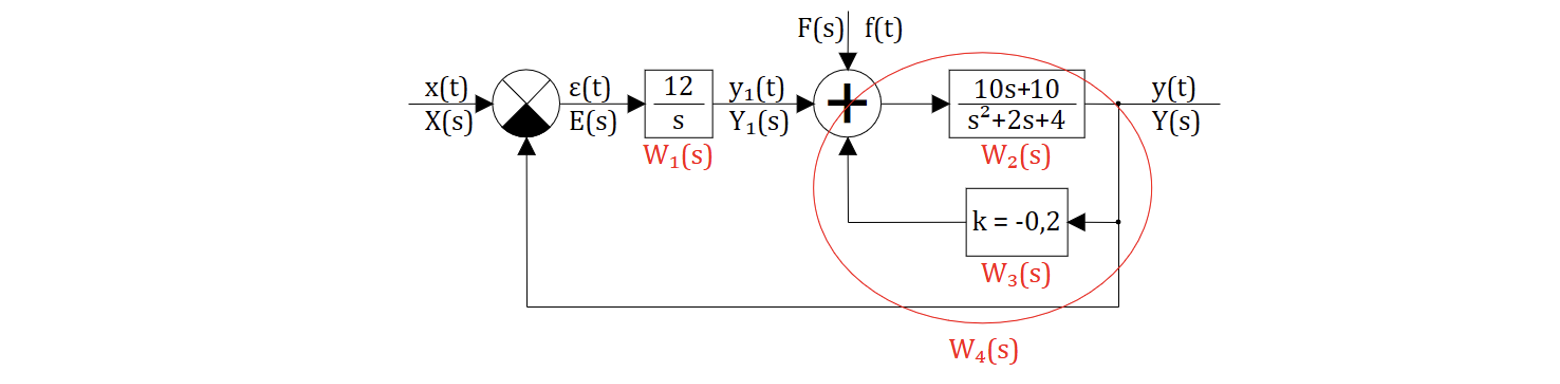
Найдем
по управляющему воздействию, выполним преобразования к общей передаточной функции.
Передаточная функция разомкнутой САР

Легко видеть, что данная САР устойчива
Т.к. система астатична по управляющему воздействию, то
Найдем . Преобразуем к свободным членам, равным единице:
Найдем
- установившуюся ошибку по возмущающему воздействию.
Используя замену цепи с местной обратной связью
, получаем следующую структурную схему:

Рисунок 7.4.6 Эквивалентная САР по возмущему воздействию
Найдем передаточную функцию по возмущающему воздействию (для замкнутой САР):
Замечаем, что САР астатична по возмущающему воздействию, т.к. числитель не имеет свободного члена.
Используя первую предельную теорему:
7.5 Установившаяся ошибка при медленно изменяющемся произвольном воздействии (коэффициенты ошибок)
Сначала прокомментируем название данного раздела:
1. произвольное воздействие – форма воздействия не соответствует любому типовому воздействию:

Причем закон изменения - не известен.
2. Медленно изменяющееся – подразумевает, что скорость протекания собственной части переходного процесса намного больше (т.е. характерная постоянная времени существенно меньше), чем скорость (относительная) изменения входного воздействия. Например, если , где
– период разгона, причем
, где
– например, время переходного процесса при подаче на вход САР ступенчатого воздействия.

Поскольку входное (управляющее) воздействие и непосредственно САР имеют значительно различающиеся постоянные времени, в первом приближении можно считать, что САР почти без инерции «отслеживает» управляющее воздействие, т.е. рассогласование можно считать приблизительно «установившимся»:
По аналогии с предыдущими подразделами:
Учитывая, что , используем обратное преобразование Лапласа:
где - весовая функция замкнутой САР для ошибки;
- свертка.
Раскрывая свертку с помощью интеграла Дюамеля-Карсона (смотри раздел 2.9), получаем:
Если , то аргумент функции
- отрицателен, следовательно
Разложим в ряд Тейлора:
Напомним сведения из математики:
Если - действительная функция, имеющая на интервале
n-ю производную, то значение функции можно расчитать по выражению:
В нашем случае в качестве переменной выступает
; в качестве
- время
; в качестве
- переменная
.
Подставляя выражение (7.5.4) в соотношение (7.5.3), получаем:
где:
Коэффициенты - называются коэффициентами ошибок.
Если аналитическое выражение - известно, то «нетрудно» рассчитать
и, соответственно, рассчитать значения коэффициентов ошибок
по выше приведенным интегралам.
Если известна экспериментально-определенная весовая (или переходная
), то расчет коэффициентов ошибок тоже не представляет проблем.
Второй способ определения установившейся ошибки при произвольном воздействии, отталкиваясь от формулы , разложим
в ряд Тейлора (а точнее в ряд Маклорена):
Подставляя последнее соотношение в формулу для рассогласования , имеем:
Замечая, что оригиналы равны:
Окончательно:
где:
Второй способ вывода явно более простой.
Коэффициенты ошибок могут быть определены и путем деления полином числителя на полином знаменателя и сравнением полученного ряда с выражением (*).
Для систем с различным порядком астатизма первые три коэффициента ошибок принимают следующие значения:
для статической САР
для астатической САР 1-го порядка
;
для астатической САР 2-го порядка
.
Пример 3
Найти установившуюся ошибку для САР, замкнутой единичной обратной связью, если разомкнутая САР состоит из последовательно-соединенных идеального интегрирующего звена и апериодического звена первого порядка
а входное управляющее воздействие
где возмущающее воздействие
, где
.

Численное решение данной задачи в видео:
Аналитическое решение
Сначала рассмотрим первую часть задачи, когда возмущающее воздействие отсутствует.
Очевидно, что данная САР имеет астатизм 1-го порядка, следовательно Тем не менее проведем эти вычисления:
где новые переменные
Найдем коэффициенты ошибок:
Найдем коэффициент :
Аналогичным путем можно найти ,
, и т.д.
Вычислим значения и
подставля занчения
Пренебрегая в первом приближении составляющими высокого порядка ( ), получаем:
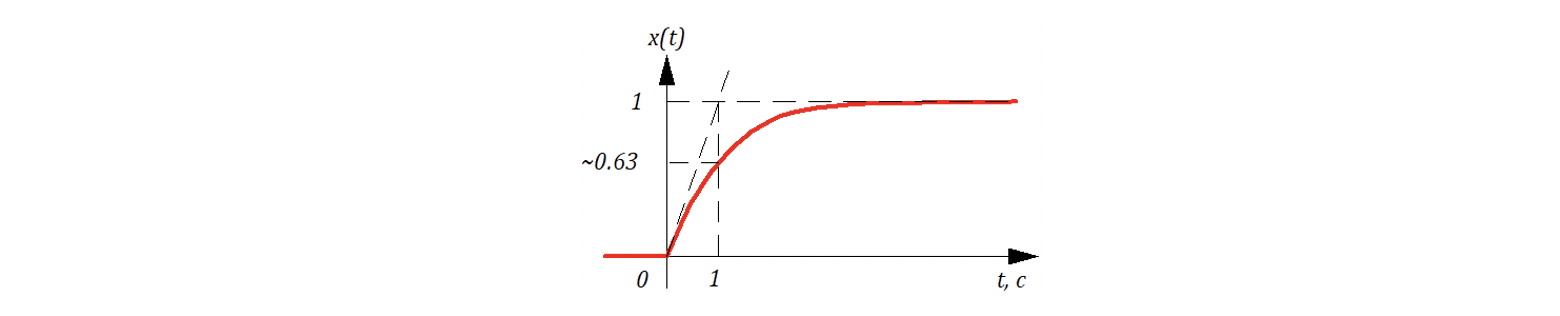
Пусть , тогда
подставляем в

Если учесть член проведя вычисления
Дифференцируя
Анализ показывает, что учитывать члены более высокого порядка нет смысла, т.к. они очень малы.
Теперь рассмотрим 2-ю часть задачи: найдем установившиеся отклонения при возмущающем воздействии
где
и нулевым входным воздействием
Найдем передаточную функцию системы для ошибки по воздействию:
где новые переменные
Найдем коэффициент ошибок:
- это означает, что рассматриваемая САР имеет астатизм по возмущающему воздействию.
Найдем :
Найдем :
Найдем :
Члены более высокого порядка не учитываем, т.к. они второго порядка малости.
- подставляя значения
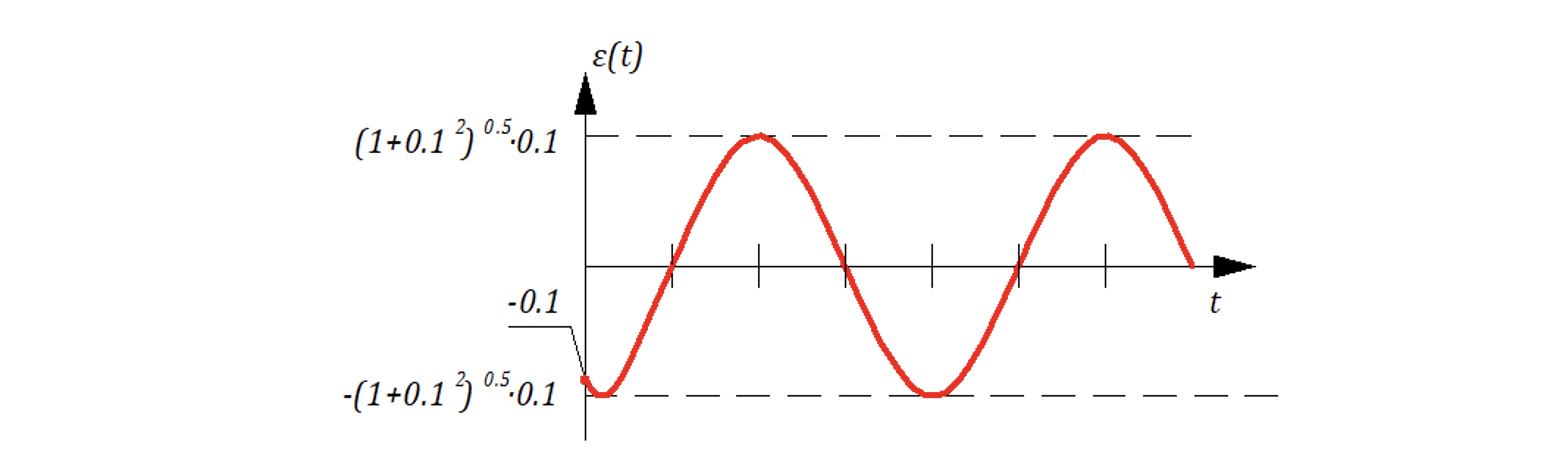
В заключение пример анализа САР по возмущающему воздействию.
В других сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1 Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2 Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3 Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4 Апериодическое звено 2-го порядка. 3.5 Колебательное звено. 3.6 Инерционно-дифференцирующее звено. 3.7 Форсирующее звено. 3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9 Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
7. Точность систем автоматического управления. Часть 1 и Часть 2
8. Качество переходного процесса. Часть 1 и Часть 2
9. Синтез и коррекция систем автоматического регулирования (САР).
10. Особые линейные системы. Часть 1