Anonymous identification for groups

Hard

13 min

362

The identification protocol based on the pairing function, resistant to impersonation and compatible with the instant digital signature (IDS) mode, was studied in this article. This protocol uses prover's and verifier's public keys. As a result, there is no anonymity, since certificates including personal data of their owners are issued for the mentioned keys. This article contains a description and analysis of new anonymous identification protocols for groups.

This publication consists of sections where we describe anonymous group identification protocols for two different scenarios, analyze the key security and resistance to impersonation, estimate the amount of information transmitted, and evaluate the optimization of computations and memory resources. At the end of this text, summary and conclusion are specified and formulated.

The term 'vanishingly small probability' (abbreviated as v.s.p.) and the boolean variable $\mathfrak{B},$ as well as public key certificates functions, were all explained in our previous article.

The following practical problem is studied in the fundamental work [RST'01]. Some party $\texttt{A},$ for example, a member of the cabinet of ministers (CM), intends to publish incriminating information about the actions of the prime minister. For this purpose, $\texttt{A}$ contacts, for example, $\texttt{B},$ a journalist from an independent media. In this case, on the one hand, it is necessary to guarantee the anonymity of the source. On the other hand, it's essential to ensure the reliability of the information provided. From the point of view of $\texttt{B},$ the information provided by a member of the CM is considered reliable.

Let's take a look at possible options.

$\texttt{A}$ cannot transmit a message signed with through a digital signature (DS) scheme, since the verification will result in de-anonymization, because $\texttt{A}’s$ personal data is included in the public key certificate. Although this method will certainly convince $\texttt{B}$ that the information comes from a member of the CM.
If $\texttt{A}$ uses anonymizing services, then all identifiers of the sender will be removed from the transmitted message. Therefore, $\texttt{B}$ will not be able to verify that the information comes from a member of the CM and won't consider it reliable.

In [RST'01] a solution has been proposed. Each member of the CM generates a DS using his personal private key, but this DS can only be verified using the personal public keys of all members of the CM, including the witness himself. As a result, $\texttt{B}$ is convinced and can also convince a third party that the information comes from the CM, but at the same time $\texttt{A}$ remains unknown.

We propose a solution to the problem formulated above through an anonymous identification protocol for groups. The advantage of our solution is that in addition to anonymous identification, $\texttt{A}$ can transmit information confidentially using a secure data transfer tunnel. The tunnel (virtual) is accessible by construction, since $\texttt{A}$ and $\texttt{B}$ are able to independently generate a shared session secret key upon successful identification. Confidentiality is guaranteed by using a symmetric cryptographic scheme.

The anonymous group identification protocol also makes it possible to convince a third party that the information received comes from a member of the CM. This follows from the fact that all public keys involved in verifying the evidence belong to members of the CM, which is easily verified using personal data from the certificates of these keys. Anonymity is based on a simple principle, which can be formulated as follows: “it is reliably known that one is from the group, but it is not known who exactly.”

The use of an anonymous group identification protocol is logically justified in the context of solving a wide range of practical problems for which compatibility with the IDS mode is essential. Some scenarios are described here.

Anonymous identification protocols for groups

The parameters used below, such as , , $\mathbb{G}_1$ , $\mathbb{G}_3$ , $\mathbb{F}_m$ , $e_m(\cdot, \cdot)$ are explained in Appendix A.

For the sake of simplicity, we omit details related to the verification of criteria needed for inclusion in the group, as well as the subsequent registration of those participants who meet them. We will proceed from the assumption that such a group has been successfully created.

For $2\leqslant n<m$ participants, represented by a set of numerators $\mathcal{I}=\{1,\ldots,n,n+1,\ldots,2n\},$ the trusted party generates a set of long-term public keys $\mathcal{P},$ a set of personal private keys of participants $\mathcal{K},$ as well as a group public key $\mathsf{Q}.$

Setup (Input: . Output: $\mathcal{P}$ , $\mathcal{K}$ , $\mathsf{Q}$ ).

$\widetilde{\mathcal{I}}=\mathcal{I}\setminus \{n+1\}=\{1, \ldots, n, n+2, \ldots, 2n\},$ $|\widetilde{\mathcal{I}}|=2n-1.$
$\alpha\in_R\!(0,m-1].$
$\omega\in_R\!(0,m-1],$ if $\omega=\alpha,$ then it chooses another $\omega.$
$\mathsf{P}_i=[\alpha^i\omega\pmod m]\mathsf{G}_1,$ $\forall i\in\widetilde{\mathcal{I}},$ if $\exists!_{i\in\widetilde{\mathcal{I}}}(\mathsf{P}_i=\infty),$ then it goes to 3.
$\gamma\in_R\!(0,m-1],$ if $(\gamma=\omega)\lor(\gamma=\alpha),$ then it chooses another $\gamma.$
$\mathsf{Q}=[\gamma\omega\alpha^{n+1}\pmod m]\mathsf{G}_1,$ if $\mathsf{Q}=\infty,$ then it goes to 5.
$s_{i}=\alpha^i\gamma\pmod m,$ $i=\overline{1,n},$ if $\exists!_{i\in[1,n]}(s_{i}=0),$ then it goes to 5.
$\mathcal{P}=\{\mathsf{P}_1,\ldots,\mathsf{P}_n,\mathsf{P}_{n+2},\ldots,\mathsf{P}_{2n}\},$ $|\mathcal{P}|=2n-1,$ $\mathcal{K}=\{s_1,\ldots, s_n\},$ $|\mathcal{K}|=n.$

The private key $s_i\in\mathcal{K}$ is delivered to the -th participant in a private way, for example, using Protocol 3 from this article. A separate certificate is issued indicating the owner’s personal data for each public key from $\{\mathsf{P}_1, \ldots, \mathsf{P}_n\}.$ In addition, a single certificate is issued for $\{\mathsf{P}_{n+2}, \ldots, \mathsf{P}_{2n}, \mathsf{Q}, n\},$ which establishes the connection between the components of this set with keys from $\{\mathsf{P}_1, \ldots, \mathsf{P}_n\}.$

The setup is performed once and ends with the removal of $\alpha,$ $\gamma,$ $\omega,$ from the local long-term secret memory of party In total, certificates are issued and maintained.

Protocol 1

Let's consider the anonymous identification protocol for the case where does not belong to the group of registered participants and $\mathsf{P}_V$ differs from the public keys from $\mathcal{P}.$ Let's suppose that owns a key pair $\{\mathbf{y},\mathsf{P}_V=[\mathbf{y}]\mathsf{G}_1\},$ where ${\mathbf{y} \in_R\!(0,m-1]}.$ The certificate $\{D_V,\mathsf{P}_V, {\Im}_{\rm{T}}\}$ is issued for $\mathsf{P}_V.$ has access to $\mathcal{S}$ and knows

Let an $\ell$ th participant act as $\ell\in\mathcal{S},$ $\mathcal{S}\subseteq\{1,\ldots,n\}.$

Protocol messages.

$P \longrightarrow V : \mathsf{S}=[\upsilon s_\ell \pmod m]\mathsf{P}_V= [\upsilon s_\ell \mathbf{y} \pmod m]\mathsf{G}_1$
$P \longleftarrow V : \mathsf{T}=[\mathbf{y}^\phi\pmod m]\mathsf{P}_V=[\mathbf{y}^{\phi+1}\pmod m]\mathsf{G}_1$
$P \longrightarrow V : g_a, \mathsf{R}=[s_\ell^{-1}]\mathsf{Q}=[\omega\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1$

Actions of the parties.

proves to that it knows the private key $s_\ell$ such that $\ell\in\mathcal{S}$ and $\mathsf{P}_\ell\in\{\mathsf {P}_1,\ldots,\mathsf{P}_n\}.$ During the proof, $\ell,$ $s_\ell$ and $\mathsf{P}_\ell$ are not revealed. The following steps are performed:

reads the current certificate $\{D_V,\mathsf{P}_V, {\Im}_{\rm{T}}\}$ and checks the DS of the trusted party $\rm{T}.$ If $\mathfrak{B}=False$ then the session ends. If $\mathfrak{B}=True,$ then it chooses ${\upsilon\in_R\!(0,m-1]}$ (commitment), computes $\mathsf{S}$ (witness), checks the condition ${\mathsf{S}\stackrel{?}\neq\infty}.$ If $\mathsf{S}=\infty,$ then selects a new $\upsilon$ and re-performs the necessary computations and checks.

reads the current certificate $\{D_V,\mathsf{P}_V, {\Im}_{\rm{T}}\}$ and checks the DS of the trusted party $\rm{T}.$ If $\mathfrak{B}=False$ then the session ends. If $\mathfrak{B}=True,$ then selects ${\phi\in_R\!(0, m-1]}$ and computes $\mathsf{T}$ (challenge). If $\mathsf{T}=\infty,$ then selects a new $\phi$ and re-performs the necessary computations and checks.
checks the integrity, authenticity and relevance of public keys $j\in\widetilde{\mathcal{S}},$ $\widetilde{\mathcal{S}}=\{\mathcal{S}\}\setminus\{\ell\},$ using the appropriate certificates. If relevance is not confirmed or $\mathfrak{B}=False,$ then the current session ends. checks the condition $\mathsf{T}\stackrel{?}\neq\infty.$ If it's true, then computes response for $\widetilde{\mathcal{S}}$ as $\{g_a=g_\ell^{-1}, \mathsf{R}\},$ where
$g_\ell=e_m([\upsilon s_\ell\pmod m]\mathsf{T}, \mathsf{G}_1+\sum_{j\in\widetilde{\mathcal{S}}}\mathsf{P}_{n+1-j})= g^{\upsilon\mathbf{y}^{\phi+1}\gamma(\alpha^\ell+\omega\sum_{j\in\widetilde{\mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}\text{,}$
otherwise the session ends.
verifies the integrity, authenticity and relevance of public keys $\mathsf{P}_{n+1-j},$ $j\in\mathcal{S},$ using the appropriate certificates. If the relevance is not confirmed or $\mathfrak{B}=False,$ then the current session ends. checks the condition $(\mathsf{S}\neq\infty)\land((g_a\neq 1)\lor(g_a\neq g)).$ If the condition is not met, the session ends. If it's met, then computes:
$g_b=e_m([\mathbf{y}^\phi\pmod m]\mathsf{S}, \mathsf{G}_1+\sum_{j\in \mathcal{S}}\mathsf{P} _{n+1-j})=g^{\upsilon\mathbf{y}^{\phi+1}\gamma(\alpha^\ell+\omega\sum_{j\in\mathcal{S}}\alpha^{n+1-j+\ell})\pmod m}\text{,}\\$
$g_c=g_bg_a=g^{\upsilon\mathbf{y}^{\phi+1}\gamma\omega(\sum_{j\in\mathcal{S}}\alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{\mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}=g^{\upsilon\mathbf{y}^{\phi+1}\gamma\omega\alpha^{n+1}\pmod m}\text{.}$

Then checks $g_c\stackrel{?}{=}e_m([\mathbf{y}^\phi\pmod m]\mathsf{S}, \mathsf{R}).$ If equal, then the proof is accepted, and rejected otherwise.

If the identification stage is successfully completed, the parties independently generate a shared session secret key in accordance with the following rules:

computes $\mathsf{A}=[\upsilon s_\ell\pmod m]\mathsf{T}=[\upsilon s_\ell\mathbf{y}^{\phi+1}\pmod m]\mathsf{G}_1.$
computes $\mathsf{B}=[\mathbf{y}^\phi\pmod m]\mathsf{S}=[\mathbf{y}^{\phi+1}\upsilon s_\ell\pmod m]\mathsf{G}_1.$

Protocol 2

Let's now consider a protocol where belongs to a group of registered participants. Then owns a key pair $\{s_c,\mathsf{P}_c\},$ where $c\in \widetilde{\mathcal{S}}$ and ${s_c=\gamma\alpha^c\pmod m},$ $\mathsf{P}_c=[\omega\alpha^c\pmod m]\mathsf{G}_1.$ The certificate $\{D_c,\mathsf{P}_c, \widehat{\Im}_{\rm{T}}\}$ is issued for $\mathsf{P}_c.$

Protocol messages.

$P \longrightarrow V : \widehat{\mathsf{S}}=[\upsilon s_\ell \pmod m]\mathsf{P}_c= [\upsilon \gamma\omega\alpha^{c+\ell}\pmod m]\mathsf{G}_1$
$P \longleftarrow V : \widehat{\mathsf{T}}=[\phi]\widehat{\mathsf{P}}_c=[\phi\gamma^{-1}\omega\pmod m]\mathsf{G}_1$
$P \longrightarrow V : \hat{g}_a, \mathsf{R}=[s_\ell^{-1}]\mathsf{Q}=[\omega\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1$

Actions of the parties.

reads the current certificate $\{D_c,\mathsf{P}_c, \widehat{\Im}_{\rm{T}}\}$ and checks the DS of the trusted party $\rm{T}.$ If $\mathfrak{B}=False,$ then the session ends. If $\mathfrak{B}=True,$ then chooses ${\upsilon\in_R\!(0,m-1]}$ (commitment), computes $\widehat{\mathsf{S}}$ (witness), checks the condition ${\widehat{\mathsf{S}}\stackrel{?}\neq\infty}.$ If $\widehat{\mathsf{S}}=\infty,$ then choses another $\upsilon$ and re-performs the necessary computations and checks.

reads the current certificate $\{D_c,\mathsf{P}_c, \widehat{\Im}_{\rm{T}}\}$ and checks the DS of the trusted party $\rm{T}.$ If $\mathfrak{B}=False,$ then the session ends. If $\mathfrak{B}=True,$ then computes ${\widehat{\mathsf{P}}_c=[s_c^{-1}]\mathsf{P}_c=[\gamma^{-1}\omega\pmod m]\mathsf{G}_1},$ chooses ${\phi\in_R\!(0, m-1]}$ and then computes $\widehat{\mathsf{T}}$ (challenge). If $\widehat{\mathsf{T}}=\infty,$ then chooses another $\phi$ and re-performs the necessary computations and checks.

checks the integrity, authenticity and relevance of public keys $\mathsf{P}_{n+1-j},$ $j\in\widetilde{\mathcal{S}},$ $\widetilde{\mathcal{S }}=\{\mathcal{S}\}\setminus\{\ell\},$ using the appropriate certificates. If relevance is not confirmed or $\mathfrak{B}=False,$ then the current session ends. checks the condition $\widehat{\mathsf{T}}\stackrel{?}\neq\infty.$ If the condition is met, then computes response for $\widetilde{\mathcal{S}}$ as $\{\hat{g}_a=\hat{g}_\ell^{-1}, \mathsf{R}\},$ where

$\hat{g}_\ell=e_m([\upsilon s_\ell\pmod m]\widehat{\mathsf{T}}, \mathsf{G}_1+ \sum_{j\in\widetilde{\mathcal{S}}}\mathsf{P}_{n+1-j})=g^{\phi\upsilon\omega(\alpha^\ell+\omega\sum_{j\in\widetilde{\mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}\text{,}$

otherwise the session ends.

verifies the integrity, authenticity and relevance of public keys $\mathsf{P}_{n+1-j},$ $j\in\mathcal{S},$ using the appropriate certificates. If the relevance is not confirmed or $\mathfrak{B}=False,$ then the current session ends. checks the condition $(\widehat{\mathsf{S}}\neq\infty)\land((\hat{g}_a\neq 1)\lor(\hat{g}_a\neq g)).$ If the condition is not met, the session ends. If it is met, then computes

$\hat{g}_b=e_m([\phi s_c^{-1}\pmod m]\widehat{\mathsf{S}}, \mathsf{G}_1+\sum_{j\in \mathcal{S}} \mathsf{P}_{n+1-j})=g^{\phi\upsilon\omega(\alpha^\ell+\omega\sum_{j\in\mathcal{S}}\alpha^{n+1-j+\ell})\pmod m}\text{,}\\$ $\hat{g}_c=\hat{g}_b\hat{g}_a=g^{\phi\upsilon\omega^2(\sum_{j\in\mathcal{S}}\alpha^{n+1-j+\ell}- \sum_{j\in\widetilde{\mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}=g^{\phi\upsilon\omega^2\alpha^{n+1}\pmod m}\text{.}$

Then checks $\hat{g}_c\stackrel{?}{=}e_m([\phi s_c^{-1}\pmod m]\widehat{\mathsf{S}}, \mathsf{R}).$ If equal, then the proof is accepted, and rejected otherwise.

If the identification stage is successfully completed, the parties independently generate a shared session secret key in accordance with the following rules:

computes $\mathsf{A}=[\upsilon s_\ell\pmod m]\widehat{\mathsf{T}}=[\phi\upsilon\alpha^\ell\omega\pmod m]\mathsf{G}_1.$
computes $\mathsf{B}=[\phi s_c^{-1}\pmod m]\widehat{\mathsf{S}}=[\phi\upsilon\alpha^\ell\omega\pmod m]\mathsf{G}_1.$

Key security

The idea is that the public key $\mathsf{P}_i$ is masked using $\omega,$ while the private key is masked using $\gamma,$ where ${\gamma, \omega\in_R\!(0,m-1]}$ and $\gamma\neq\omega\neq\alpha$ by construction. This means that the complexity of revealing all with a known ECDLP/DLP solution for the public key from $\mathcal{P},$ as well as a known private key from $\mathcal{K},$ is not less than the complexity of finding a ECDLP/DLP solution.

Let's consider a particular case. Let us assume that $s_1=\gamma\alpha\pmod m$ and $\varphi_1=\alpha\omega\pmod m$ are known, where $\varphi_1$ is the ECDLP/DLP solution subject to $\mathsf{P}_1$ or $e_m(\mathsf{ P}_1, \mathsf{G}_1).$ Then

$\alpha={\varphi_1\omega^{-1}\pmod m}=s_1\gamma^{-1}\pmod m,$ $\omega={\varphi_1\alpha^{-1}\pmod m},$ $\gamma=s_1\alpha^{-1}\pmod m$ and $\psi={s_1\varphi_1^{-1}\pmod m}=\gamma\omega^{-1}\pmod m,$ $\psi'=s_1^{-1}\varphi_1\pmod m=\gamma^{-1}\omega\pmod m.$ Consequently, if $\varphi_1$ and are known, then it is enough to find $\alpha\lor\gamma\lor\omega$ to reveal all $2\leqslant i\leqslant n.$

Note that the adversary has additional capabilities. Let and $\varphi_u$ be known such that $u=2^{2^w},$ $u\in[2,n],$ $0\leqslant w\leqslant\lfloor\log_2{\log_2 {n}}\rfloor.$ The adversary's motivation is that with known $\varphi_u$ and (the square root is calculated once if ), it is possible to reveal $\alpha$ using the iterative method of taking a square root using the Tonelli-Shanks algorithm of asymptotic complexity $O((\log_{2}{m})^2)$ [C'06] (section 11.1.5).

For example, with known $\omega,$ $\alpha=\sqrt{\cdots\sqrt{\varphi_u\omega^{-1}\pmod m}}$ and $\gamma={s_u\varphi_u^{-1} \omega\pmod m}.$ In general, it is not known how to take the root of an arbitrary degree in $\mathbb{F}_m^*.$

Brute force attacks for some $\varphi_u,$ are listed in Appendix C. Frontal attack (Algorithm 1) is not considered optimal, since on average it will take trials, where

Let's suppose that there is a number $\mathsf{a}$ such that $\mathsf{a}\equiv\varphi_u\pmod m$ and a factorization $\mathsf{a}=\prod_{j=1}^t\mathsf{p}_j^{r_j}$ is known, $\mathsf{p}_j$ are different primes, ${r_j,t\in\mathbb{N}}.$

Such factorization can be obtained by using, for example, the number field sieve method or another well-known method [I'11]. Let the set $\mathcal{D}=\{\mathsf{p}_1^{r_1}, \ldots, \mathsf{p}_t^{r_t}\}$ be given. If all are known, then the following representation is true:

$\widehat{\mathcal{D}}=\{\underbrace{\mathsf{p}^{\mathstrut}_1,\ldots,\mathsf{p}^{\mathstrut}_1}_{r_1}, \ldots, \underbrace{\mathsf{p}^{\mathstrut}_t, \ldots, \mathsf{p}^{\mathstrut}_t}_{r_t}\},$ $|\widehat{\mathcal{D}}|=\sum_{j=1}^t r_j=d.$

Let us enumerate the prime numbers from $\widehat{\mathcal{D}}$ by integers from to and move to the set $\widetilde{\mathcal{D}}=\{\tilde{\mathsf{p}} ^{\mathstrut}_1, \ldots, \tilde{\mathsf{p}}^{\mathstrut}_d\}.$

Let's estimate the complexity of the optimized brute force (Algorithm 2). The attack uses the auxiliary sequence $\mathbf{b}=(b_1, \ldots, b_d),$ $b_j\in\{0,1\}.$ The Hamming weight $\mathbf{b}$ varies in the range from to $\lceil d/2 \rceil$ and the number of trials is limited above by

$A=\sum_{j=1}^{\lceil d/2 \rceil}C_d^j. \hspace{3.5cm}\text{(1)}$

On average, it takes trials to find $\alpha,$ $\omega,$ $\gamma.$

Let's suppose that $\alpha=\tilde{\mathsf{p}}_{1}^{\mathsf{x}}\pmod m$ and $\omega=\tilde{\mathsf{p}}_{2}^{\mathsf{y}}\pmod m,$ $\mathsf{x}, \mathsf{y}\in\mathbb{N}.$ Let us recall that $\alpha\neq\omega$ by construction, and the following options are also possible:

$\tilde{\mathsf{p}}_{1}=\tilde{\mathsf{p}}_{2}$ $\Rightarrow$ $((\mathsf{x}\geqslant 1)\land(\mathsf{y}\geqslant \mathsf{x}+1))\lor((\mathsf{y}\geqslant 1)\land(\mathsf{x}\geqslant \mathsf{y}+1)).$
$\tilde{\mathsf{p}}_{1}\neq\tilde{\mathsf{p}}_{2}$ $\Rightarrow$ $(\mathsf{x}\geqslant 1)\land(\mathsf{y}\geqslant 1).$

Let's denote the number of primes in the range as $\pi(M).$ According to Chebyshev's estimates ${0.92\times\frac{M}{\ln M}<\pi(M)<1.06\times\frac{M}{\ln M}}.$ Therefore, $2<d\leqslant\pi(M).$

It is well known that $\sum_{j=0}^d C_d^j=2^d,$ but in (1) approximately half of all possible binomial coefficients are summed up and therefore Thus, $\forall_{d\leqslant\lceil \log_2{M}\rceil}A<M.$

The cardinality of the set $\widetilde{\mathcal{D}}$ cannot be controlled if $\alpha, \omega\in_R\!(0,m-1].$ As a result, may be small and the complexity of a brute force, meaning the number of trials will not provide the required security level.

Let's act as follows in order to improve the situation. At the setup stage, let the trusted party randomly select $d\leqslant \pi(M)$ distinct primes from the range and make the set $\widetilde{\mathcal{D}}.$ The primality test is performed using the technique from [AKS'04]. For example, if $m\sim 2^{160},$ then $1.2\times10^{46} < \pi(M) < 1.4\times10^{46}.$ Then generates a random binary sequence $\mathbf{b}$ of Hamming weight $\lceil d/2 \rceil,$ where $b_j\in_R\!\{0, 1\},$ and for a given $\widetilde{ \mathcal{D}}$ computes:

$\alpha=\prod_{j=1}^d\tilde{\mathsf{p}}_j^{b_j}\pmod m$ and $\omega=\prod_{j=1 }^d\tilde{\mathsf{p}}_j^{\bar{b}_j}\pmod m,$ $\forall_{j\in[1,d]}\bar{b}_j=b_j\oplus 1.$

Now the complexity of the brute force mentioned above is limited by the guaranteed value $B=C_d^{\lceil d/2 \rceil}$ and $2^d>A>B\geqslant\frac{2^d}{d+1}.$

In general, $C_d^{[ad]}=\left(\frac{1}{a^a(1-a)^{1-a}}+o(1)\right)^d,$

where $a\in(0,1),$ is a certain function whose modulus tends to zero and can take on both negative and positive values. If then For example, to ensure a -bit security level or higher, it's necessary to choose $d\geqslant84.$

The complexity of finding $\alpha\lor\omega\lor\gamma$ under the condition $\widetilde{\mathcal{D}}$ is equivalent to the well-known -complete problem Subset Product [GJ'79] (SP14, p. 224) or, in another way, Product of Dimensions [GJ'82] (MP 14, page 283). -completeness is proven by reducing another -complete problem known as Exact Coverage by 3-Sets [GJ'82] (TP-3, page 73) to this problem. It should be noted that MP 14 is a problem with numerical parameters and -completeness does not exclude solving this problem using a pseudopolynomial time complexity algorithm under the condition $P\neq NP$ [GJ'82] (section 4.2 on page 117, commentary to MP 14 on page 283), which depends on and $\max(\tilde{\mathsf{p}}_1, \ldots, \tilde{\mathsf{p}}_d).$ Obviously, the existence of an algorithm of such complexity provides the adversary with additional opportunities. However, this drawback is eliminated if chooses primes from the range $[\lceil\sqrt{\mathstrut{m}}\rceil, M],$ and the value of is such that it compensates for the decrease in security level due to the existence of a pseudo-polynomial complexity algorithm. The value of is limited below by the security level. Then can choose an arbitrarily large subject to a given security level as a necessary condition. The set $\widetilde{\mathcal{D}}$ is created once at the setup and its cardinality, as well as the bitlength of the prime numbers included, does not affect the performance characteristics of the identification protocol. The number of primes in the mentioned range does not differ in order of magnitude from $\pi(M).$ With -bit security level, the length of prime numbers will vary from to bits.

Grover's algorithm [G'96] allows to find $\alpha\lor\omega\lor\gamma$ under the condition $\widetilde{\mathcal{D}}$ in $O(\sqrt{B})$ trials on a quantum computer with qubits. If a brute force on a quantum computer seems realistic, then it's necessary to choose such a value of that it could compensate for the decrease in security as a result of using Grover's algorithm. For example, a security level of bits inclusive and higher is provided with $d\geqslant 164.$

In [S'97] it is demonstrated that on a quantum computer the complexity of such intractable problems as factorization, DLP, and also ECDLP due to the existence of a bilinear mapping $e_m:\mathbb{G}_1\times \mathbb{G}_1\mapsto \mathbb {G}_3,$ is limited by some polynomial of the input size.

Let's note that the set $\widetilde{\mathcal{D}}$ is intended solely for obtaining $\alpha,$ $\omega,$ on the basis of which $\mathsf{P}_i,$ are then computed. Once all necessary computations are complete, removes $\widetilde{\mathcal{D}}$ from local long-term memory.

Why does it work

It's worth noting that the anonymous group identification protocol is based on the ideas revealed in [BGW'05].

Let's dive inside it and look at the function ${\eta=n+1-j+\ell},$ which appears in the exponent of $\alpha$ when $g_\ell$ and as well as $\hat{g}_ \ell$ and $\hat{g}_b$ being computed.

The function $\eta$ is continuous, and, for analysis purposes, it is enough to look at the Table #1 containing values for some enumerators from the integer interval

Let $\mathcal{S}=\{1,\ldots,n\},$ $\ell\in \mathcal{S}$ and $\widetilde{\mathcal{S}}=\{\mathcal{S} \}\setminus\{\ell\}.$ According to the Table 1, $\eta=n+1$ is located on the main diagonal and meet the criteria $j=\ell,$ $\ell\neq 0$ by construction and therefore $\eta\in[2,2n].$

Since $\widetilde{\mathcal{S}}$ lacks the $\ell$ th numerator, but $\mathcal{S}$ contains the numerator $j=\ell,$ then

$\sum_{j\in \mathcal{S}}\alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{\mathcal{S}}}\alpha^{n+1-j+\ell}=\alpha^{n+1}.$

In $\mathcal{S},$ the non-decreasing order of the numerators is chosen to simplify explanations. It's worth noting that the protocol is invariant regarding this order. Moreover, the protocol works correctly with the subset $\mathcal{S}_\wp\subseteq\mathcal{S}.$ The asymptotic estimate for the number of such subsets is These subsets may either intersect or not.

Example

Let's suppose that $\mathcal{S}=\{1,2,3,\ldots,8,9,10\}$ and There is some subset ${\mathcal{S}_\wp\subset\mathcal{S}}$ such that

$\mathcal{S}_\wp=\{3,7,5,8,4,2\}.$ Let $\ell=7,$ then $\widetilde{\mathcal{S}}_\wp=\{3,5,8,4,2\}.$ Therefore,

$\sum_{j\in\mathcal{S}_\wp}\alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{\mathcal{S}_\wp}}\alpha^{n+1-j+\ell}=$

$\alpha^{11-3+7}+$

$\alpha^{11-7+7}+$

$\alpha^{11-5+7}+$

$\alpha^{11-8+7}+$

$\alpha^{11-4+7}+$

$\alpha^{11-2+7}-$

$\alpha^{11-3+7}-$

$\alpha^{11-5+7}-$

$\alpha^{11-8+7}-$

$\alpha^{11-4+7}-$

$\alpha^{11-2+7}=\alpha^{11}.$

Preliminary analysis

Let's suppose that the adversary knows $\ell$ and $\varphi_\ell$ is a ECDLP/DLP solution subject to $\mathsf{P}_\ell$ or $e_m(\mathsf{P}_\ell, \mathsf{G}_1).$ Then in Protocol 1 the adversary on behalf of computes witness as $\mathsf{S}'={[\upsilon \varphi_\ell \pmod m]\mathsf{P}_V}= [\upsilon\alpha^\ell\omega \mathbf{y}\pmod m] \mathsf{G}_1.$ Moreover, computes response as

$\{\acute{g}_a=\acute{g}_\ell^{-1},$ $\mathsf{R}'=[\varphi_\ell^{-1}]\mathsf{Q}=[\gamma\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1\},$ where

$\acute{g}_\ell=e_m([\upsilon \varphi_\ell\pmod m] \mathsf{T}, \mathsf{G}_1+\sum_{j\in\widetilde{ \mathcal{S}}} \mathsf{P}_{n+1-j})=g^{\upsilon\mathbf{y}^{\phi+1}\omega(\alpha^\ell+\omega\sum_{j\in\widetilde{ \mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}\text{.}$

In its turn, computes

$\acute{g}_b=e_m([\mathbf{y}^\phi\pmod m] \mathsf{S}', \mathsf{G}_1+\sum_{j\in \mathcal{S}} \mathsf{P}_{n+1-j})=g^{\upsilon\mathbf{y}^{\phi+1}\omega(\alpha^\ell+\omega\sum_{j\in \mathcal{S}}\alpha^{n+1-j+\ell})\pmod m}\text{,}\\$ $\acute{g}_c=\acute{g}_b\acute{g}_a=g^{\upsilon\mathbf{y}^{\phi+1}\omega^2(\sum_{j\in \mathcal{S}}\alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{ \mathcal{S}}} \alpha^{n+1-j+\ell})\pmod m}=g^{\upsilon\mathbf{y}^{\phi+1}\omega^2\alpha^{n+1}\pmod m}\text{.}$

Therefore, $\grave{g}=e_m([\mathbf{y}^\phi\pmod m] \mathsf{S}', \mathsf{R}')=g^{\upsilon\mathbf{y}^{\phi+1}\omega\gamma\alpha^{n+1}\pmod m}$ and $\acute{g}_c=\grave{g}$ with v.s.p.

In order to deceive the verifier, the adversary needs to reveal $\gamma$ and $\omega,$ then

$\mathsf{R}'={[\gamma^{-1}\omega\varphi_\ell^{-1}\pmod m]\mathsf{Q}}=[\omega\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1$ and $\acute{g}_c=\grave{g}.$

In Protocol 2 witness and response are computed as $\widehat{\mathsf{S}}'=[\upsilon\varphi_\ell \pmod m]\mathsf{P}_c= {[\upsilon\omega^2\alpha^{c+\ell}\pmod m] \mathsf{G}_1}$ and $\{\check{g}_a=\check{g}_\ell^{-1},$ $\mathsf{R}'=[\varphi_\ell^{-1}]\mathsf{Q}=[\gamma\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1\},$ respectively, where

$\check{g}_\ell=e_m([\upsilon \varphi_\ell\pmod m]\widehat{ \mathsf{T}}, \mathsf{G}_1+\sum_{j\in\widetilde{ \mathcal{S}}} \mathsf{P}_{n+1-j})=g^{\phi\upsilon\gamma^{-1}\omega^2(\alpha^\ell+\omega\sum_{j\in\widetilde{ \mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}\text{.}$

computes

$\check{g}_b=e_m([\phi s_c^{-1}\pmod m]\widehat{ \mathsf{S}}', \mathsf{G}_1+\sum_{j\in \mathcal{S}} \mathsf{P}_{n+1-j})=g^{\phi\upsilon\gamma^{-1}\omega^2(\alpha^\ell+\omega\sum_{j\in \mathcal{S}}\alpha^{n+1-j+ \ell})\pmod m}\text{,}\\$ $\check{g}_c=\check{g}_b\check{g}_a=g^{\phi\upsilon\gamma^{-1}\omega^3(\sum_{j\in \mathcal{S}}\alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{ \mathcal{S}}} \alpha^{n+1-j+\ell})\pmod m}=g^{\phi\upsilon\gamma^{-1}\omega^3\alpha^{n+1}\pmod m}\text{.}$

Therefore, $\bar{g}=e_m([\phi s_c^{-1}\pmod m]\widehat{ \mathsf{S}}', \mathsf{R}')=g^{\phi\upsilon\omega^2\alpha^{n+1}\pmod m}$ и $\check{g}_c=\bar{g}$ with v.s.p.

In order to deceive the verifier, the adversary needs to reveal $\gamma$ and $\omega,$ then

$\mathsf{R}'={[\gamma^{-1}\omega\varphi_\ell^{-1}\pmod m]\mathsf{Q}}=[\omega\alpha^{n+1-\ell}\pmod m]\mathsf{G}_1$ и $\check{g}_c=\bar{g}.$

Let's recall that, in order to reveal $\gamma$ and $\omega,$ it's necessary to find a solution to a specific -complete problem given the known $\varphi_u$ and

Let a malicious verifier owns the key pair $\{\mathbf{\acute{y}},\mathsf{P}_{V'}=[\mathbf{\acute{y}}]\mathsf{G} _1\}.$ Let's evaluate potential risks associated with impersonating the verifier, namely replacing with

Protocol 1

To impersonate the verifier, it is necessary to find a ECDLP/DLP solution subject to $\mathsf{P}_V$ or $e_m(\mathsf{P}_V, \mathsf{G}_1).$ Then $\mathsf{S}'=[\mathbf{y}^{-1}\mathbf{\acute{y}}\pmod m]\mathsf{S}={[\upsilon s_\ell\pmod m] \mathsf{P}_{V'}}.$ The relationship between ECDLP and DLP is explained in Appendix A.

Let's assume that the ECDLP/DLP solution mentioned above is not known. However, the adversary has access to $\mathsf{P}_{V'}$ and is able to impose $\mathsf{T}'=[\phi']\mathsf{P}_{V'}$ instead of $\mathsf{T}$ and $\mathsf{S}'=[\upsilon']\mathsf{P}_{V'}$ $\mathsf{S}$ instead of $\mathsf{S},$ where $\phi'=\mathbf{y}^\phi\pmod m$ and $\upsilon'=\upsilon s_\ell\pmod m$ with v.s.p. Then computes response as $\acute{g}_a=\acute{g}_\ell^{-1},$ $\mathsf{R},$ where

$\acute{g}_\ell=e_m([\upsilon s_\ell\pmod m] \mathsf{T}', \mathsf{G}_1+\sum_{j\in\widetilde{ \mathcal{S}}} \mathsf{P}_{n+1-j})=g^{\phi'\upsilon\gamma\acute{\mathbf{y}}(\alpha^\ell+\omega\sum_{j\in\widetilde{ \mathcal{S}}}\alpha^{n+1-j+\ell})\pmod m}\text{.}$

computes

$\acute{g}_b=e_m([\phi'\pmod m] \mathsf{S}', \mathsf{G}_1+\sum_{j\in \mathcal{S}} \mathsf{P}_{n+1-j})=g^{\phi'\upsilon'\acute{\mathbf{y}}(1+\omega\sum_{j\in \mathcal{S}}\alpha^{n+1-j})\pmod m}$

and $\acute{g}_c=\acute{g}_a\acute{g}_b.$ Obviously, $\acute{g}_c=g_c$ and $\acute{g}_c=e_m([\phi'] \mathsf{S}', \mathsf{R})$ with v.s.p.

Let's assume that the adversary imposes $\widetilde{\mathsf{T}} = [\phi']\mathsf{P}_V,$ but doesn't substitute $\mathsf{S},$ then

$\acute{g}_b=e_m([\phi'\pmod m] \mathsf{S}, \mathsf{G}_1+\sum_{j\in \mathcal{S}} \mathsf{P} _{n+1-j})=g^{\phi'\upsilon\gamma\mathbf{y}(\alpha^\ell+\omega\sum_{j\in \mathcal{S}}\alpha^{n+1-j+\ell})\pmod m}\text{,}\\$ $\acute{g}_c=\acute{g}_b\acute{g}_a=g^{\phi'\upsilon\mathbf{y}\gamma\omega(\sum_{j\in \mathcal{S}} \alpha^{n+1-j+\ell}-\sum_{j\in\widetilde{ \mathcal{S}}} \alpha^{n+1-j+\ell})\pmod m}=g^{\phi'\upsilon\gamma\mathbf{y}\omega\alpha^{n+1}\pmod m}.$

If the final check is performed by then $\acute{g}_c=e_m([\mathbf{y}^{\phi}\pmod m] \mathsf{S}, \mathsf{R})$ with v.s.p. If such a check is performed by someone who knows $\phi',$ for example then $\acute{g}_c=e_m([\phi'] \mathsf{S}, \mathsf{R}).$ However, despite the fact that the proof is accepted by impersonation does not take place, since is not substituted.

Then computes $\mathsf{A}'=[\upsilon s_\ell\pmod m]\mathsf{T}'=[\upsilon s_\ell\mathbf{y}\phi'\pmod m]\mathsf {G}_1$ and computes $\mathsf{B}=[\mathbf{y}^{\phi}\pmod m]\mathsf{S}=[\mathbf{y}^{\phi+1 }\upsilon s_\ell\pmod m]\mathsf{G}_1.$

Therefore, $\mathsf{A}=\mathsf{B}'$ with v.s.p. will not be able to reveal the session secret key, since this requires knowing $\mathbf{y}.$ However, knows $\acute{\mathbf{y}}$ and can compute $\mathsf{B}'=[\acute{\mathbf{y}}\phi'\pmod m]\mathsf{S}=[\acute{\mathbf{y}}\phi'\upsilon s_\ell\pmod m]\mathsf{G}_1,$ but since $\acute{\mathbf{y}}=\mathbf{y}$ with v.s.p., then $\mathsf{A}'=\mathsf{B}'$ with v.s.p.

Protocol 2

Let's suppose that ${\varphi_c=\omega\alpha^c\pmod m}$ is a ECDLP/DLP solution subject to $\mathsf{P}_c$ or $e_m(\mathsf{P}_c, \mathsf{G}_1).$ Then $\widehat{\mathsf{S}}'=[\varphi_c^{-1}\acute{\mathbf{y}}\pmod m]\widehat{\mathsf{S}}=[\upsilon s_\ell \pmod m]\mathsf{P}_{V'},$ but in order to compute $\widehat{\mathsf{T}}'=[\phi'\gamma\omega^{-1} \acute{\mathbf{ y}}\pmod m]\widehat{\mathsf{P}}_c=[\phi']\mathsf{P}_{V'},$ where $\phi'=\phi$ with v.s.p., it is necessary to know $\gamma$ and $\omega.$ As demonstrated above, the revelation of them requires to solve a specific -complete problem under the condition that $\varphi_u$ and are known.

In the light of the explanation given above, further considerations regarding impersonation do not make sense.

Amount of information transmitted

When a compact representation is used, then, in order to deliver $\mathsf{S},$ $\mathsf{T},$ $\mathsf{R},$ in Protocol 1, as well as $\widehat{\mathsf{S}},$ $\widehat{\mathsf{T}},$ $\mathsf{R},$ $\hat{g}_a$ in Protocol 2, one will need to transmit $3(\lceil\log_{2}{p}\rceil+1)+ k\lceil\log_{2}{p}\rceil+\lambda$ bits, where $\lambda$ is the bitlength of the binary representation of serial numbers of certificates $\{D_V,\mathsf {P}_V, \Im_{\rm{T}}\}$ and $\{D_c,\mathsf{P}_c, \widehat{\Im}_{\rm{T}}\},$ and is the embedding degree ( $g_a, \hat{g}_a\in\mathbb{G}_3$ ). Explanations regarding the embedding degree are provided in Appendix A.

If some random subset $\mathcal{S}_\wp\subseteq\mathcal{S}$ is involved, then it is necessary to notify about the enumerators included in this subset. To do this, must additionally transmit bits of information, where

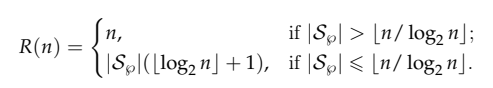
When bits are transmitted, the numerators from $\mathcal{S}_\wp$ correspond to the positions where the binary units are located.

On the other hand, it is reasonable to estimate the amount of information required for the transmission of only protocol messages, since this subset is either fixed or changes slowly over time for most practical applications, although must know which numerators are included in $\mathcal{S}_\wp\subseteq\mathcal{S},$ and therefore somehow obtain the relevant information. Therefore, it is enough to transmit information about numerators once. When estimating, we can neglect the amount of information that needs to be transmitted to modify such a slowly changing subset.

Computational optimization

$\mathcal{S}$ is fixed in a number of practical applications. For example, when some sets of public keys, used for verification, are assigned to individual structural divisions of a corporation or government agency. In this case, there is no need to report the numerators from $\mathcal{S}$ each time, since the set of necessary public keys is predefined.

If you commit $\mathcal{S},$ then you can proactively confirm the authenticity, integrity and relevance of public keys $\mathsf{P}_{n+1-j},$ $j\in\mathcal{S},$ using corresponding certificates.

Then it's necessary to compute and publish the point $\mathsf{M}=\sum_{j\in \mathcal{S}} \mathsf{P}_{n+1-j}.$ Then the $\ell$ -th prover computes the point $\mathsf{K}_\ell=\sum_{j\in\widetilde{ \mathcal{S}}} \mathsf{P}_{n+1-j}$ in advance and stores it in local long-term secret memory. Assuming that Protocol 1 is initiated, then in the case of the $\ell$ -th prover computes $g_\ell={e_m([\upsilon s_\ell\pmod m] \mathsf{T}, \mathsf{G}_1+ \mathsf{K}_\ell)}$ and computes $g_b={e_m([\mathbf{y}^\phi\pmod m]\mathsf{S}, \mathsf{ G}_1+\mathsf{M})}.$

The optimization is relevant for both Protocol 1 and Protocol 2.

If always belongs to a group of registered participants and Protocol 2 is initiated, then an optimization is possible that relies on the following rationale.

The embedding degree as well as the field characteristic determine the complexity of the DLP in $\mathbb{G}_3.$ For a fixed the larger the higher the complexity of individual pairing, as well as various arithmetic operations in $\mathbb{G}_3,$ including discrete exponentiation and multiplicative inversion. Since for Protocol 2 the subexponential complexity of finding a DLP solution is not critical, it is reasonable to reduce the complexity of arithmetic operations, as well as reduce the memory resource by using small values of

Conclusions

Regarding the key security, Protocol 1 and Protocol 2 are presumably consistent with the basic imperative of post-quantum cryptography, where the rationale for security is to prove that an attack on a cryptosystem consists of finding a solution to some problem that is hypothetically intractable on a quantum computer. -complete problems under the condition $P\neq NP$ fully comply with this statement.

Since the ECDLP/DLP solution for an arbitrary public key from $\mathcal{P}$ does not allow revealing the corresponding private key due to special masking techniques, we assumed that in addition to the solution $\varphi_u,$ the private key is also known. It is demonstrated that even with such assumptions, it is necessary to find a solution to a specific -complete problem to reveal all other private keys.

We emphasize that the choice of numbers $u=2^{2^w},$ $u\in[2,n],$ is limited. There are few such numbers, for example, if we put $n=2^{16},$ then the numbers from the set $\{2, 2^2, 2^4, 2^8, 2^{16}\}$ are available. Expansion of this set is unlikely, since groups with the number of participants $n=2^{32}$ and more are rarely encountered in practice.

Consequently, the adversary's options are also limited.

It should be noted that Protocol 1 allows impersonation with the known ECDLP/DLP solution. This is because the verifier's private and public keys do not have additional masking, unlike the keys used in Protocol 2.

The anonymous group identification protocol described and analyzed in this article effectively distinguishes itself by the security level from the functionally similar protocol in this article. This distinction arises because the security of the latter is solely determined by the complexity of finding an ECDLP/DLP solution.

Final findings

IDS-compatible anonymous identification protocols for groups have been designed and studied. It is demonstrated that the key security is determined by the complexity of finding a solution to a specific -complete problem.

The text of the article in pdf format can be downloaded here.

References

[RST'01] Rivest, Ronald L., Shamir, A., Tauman, Y. "How to leak a secret: Theory and applications of ring signatures." In $\textit{Advances in Cryptology — ASIACRYPT'01},$ LNCS 3895, (2001) 164-186.

[C'06] Cohen, H., Frey, G., Avanzi, R., Doche, C., Lange, T., Nguyen, K., Vercauteren, F. $\textit{Handbook of Elliptic and Hyperelliptic Curve Cryptography},$ Chapman and Hall/CRC, 2006.

[AKS'04] Agrawal, M., Kayal, N., Saxena, N. "PRIMES is in P." $\textit{Annals of Mathematics},$ v.160, (2004) 781-793.

[I'11] Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие. — Казань: Казан. ун-т, 2011. 200 с.

[GJ'79] Garey, M. R. and Johnson, D. S. A Guide to the Theory of -Completeness. W. H. Freeman&Co., New York, NY, 1979.

[G'96] Grover, L. "A fast quantum mechanical algorithm for database search." Proceedings of $\textit{28th Annual ACM Symposium on the Theory of Computing (STOC)},$ (1996) 212-219. https://arxiv.org/abs/quant-ph/9605043.

[S'97] Shor, Peter W. "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer." $\textit{SIAM Journal on Computing},$ v.26, 5, (1997) 1484-1509.

[BGW'05] Boneh, D., Gentry, C. and Waters, B. "Collusion Resistant Broadcast Encryption With Short Ciphertexts and Private Keys." In $\textit{Proceedings of Crypto 2005},$ LNCS 3621, (2005) 258-275.

Tags:

Hubs:

Information Security