 В прошлый раз мы говорили о том, что число бинарных деревьев с n вершинами равно C(n), где C(n) – это n-ое число Каталана. Я заинтересовался чего больше: произвольных деревьев из n вершин или бинарных деревьев из n вершин. Ответ может вас удивить, он не лежит на поверхности.
В прошлый раз мы говорили о том, что число бинарных деревьев с n вершинами равно C(n), где C(n) – это n-ое число Каталана. Я заинтересовался чего больше: произвольных деревьев из n вершин или бинарных деревьев из n вершин. Ответ может вас удивить, он не лежит на поверхности.
Распространённый ответ на этот вопрос я получу сразу: «Разумеется, произвольных деревьев больше, т.к. бинарное дерево – это частный случай произвольного дерева». Можете ли вы сказать, почему это неверно? Бинарных деревьев больше, чем произвольных деревьев! Существует два бинарных дерева из двух вершин: одно с левым потомком ребёнком корня, а другое – с правым потомком корня. Но есть только одно произвольное дерево с двумя вершинами, в нём нет разницы между «левым» и «правым» потомком.
Как оказалось, ответ на мой вопрос (кроме вырожденных случаев деревьев из нуля вершин и одной вершины) заключается в том, что бинарных деревьев из n вершин всегда больше, чем произвольных деревьев из n вершин.
Если вы исследуете эту задачу, то заметите интересный факт: число произвольных деревьев из n вершин равно С(n-1). Существует 14 бинарных деревьев из 4 вершин и 14 произвольных деревьев из 5 вершин. Существует 1430 бинарных деревьев из 8 вершин и 1430 произвольных деревьев из 9 вершин. Чудно!
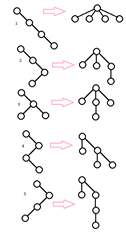
Очевидно, что это не может быть совпадением. Должно быть взаимнооднозначное соответствие между бинарными деревьями размера n и произвольными деревьями размера n+1. И в самом деле, в существовании соответствия легко убедиться, если посмотреть на картинки. Слева находится изображение первых 5 бинарных деревьев размера 4, а рядом – пять соответствующих произвольных деревьев размера 5.
Чтобы сделать соответствие более понятным посмотрим на изображение справа. Для перехода из бинарного дерева в соответствующее произвольное дерево нужно повернуть бинарное дерево на 45 градусов против часовой стрелки, добавить сверху корень, а затем исправить все горизонтальные линии так, чтобы они указывали на родителей.
Или, с точки зрения структур данных, можно представить каждую вершину в произвольном дереве, как ссылку на первого ребёнка и ссылку на следующего брата. Получилось в точности бинарное дерево, только вместо надписей на вершинах «первый ребёнок» и «следующий брат» нужно написать «левый потомок» и «правый потомок». Есть только одно отличие между бинарным деревом и произвольным деревом в этой системе – правый потомок корня всегда пуст, т.к. корень не имеет братьев. Теперь вы ведете, что отличие между бинарным деревом и произвольным деревом состоит в именах полей в структуре данных, а значит мы показали взаимнооднозначное соответствие между ними.
Таким образом, мы получили решение второй части моей задачи. У нас есть механизм, который пронумеровывает все бинарные деревья и взаимнооднозначное соответствие между бинарными деревьями и произвольными деревьями. Все что осталось сделать – получить механизм превращения бинарного дерева в соответствующее произвольное дерево. Оставим это в качестве упражнения, но ради интереса приведём здесь механизм, который превращает бинарное дерево в строковое представление соответствующего произвольного дерева, использую компактный синтаксис для произвольного дерева, о котором я говорил в прошлый раз.
public static string TreeString(Node node)
{
// Получение строкового представления произвольного дерева
// по бинарному дереву.
var sb = new StringBuilder();
Action<Node> f = null;
f = n =>
{
sb.Append("{");
for (Node child = n.Left; child != null; child = child.Right)
f(child);
sb.Append("}");
};
f(new Node(node, null));
return sb.ToString();
}
* This source code was highlighted with Source Code Highlighter.Для получения всех деревьев размера 5, мы переберём все бинарные деревья размера 4 и выведем соответствующие произвольные деревья размера 5.
foreach (var n in AllBinaryTrees(4))
Console.WriteLine(TreeString(n));
* This source code was highlighted with Source Code Highlighter.и мы получим
{{}{}{}{}}
{{}{}{{}}}
{{}{{}}{}}
{{}{{}{}}}
{{}{{{}}}}
{{{}}{}{}}
{{{}}{{}}}
{{{}{}}{}}
{{{{}}}{}}
{{{}{}{}}}
{{{}{{}}}}
{{{{}}{}}}
{{{{}{}}}}
{{{{{}}}}}
Обратите внимание, что если вы уберёте крайние скобки, то мы получим решение задачи «напечатать все правильные комбинации из четырёх пар скобок»! Если вы пронумеруете все бинарные деревья, тогда вы пронумеруете все решения множества различных эквивалентных задач.
В следующий раз: что мы можем сгенерировать ещё?