Comments 47
(h ∘ g) ∘ f = h ∘ (g ∘ f) = h ∘ g ∘ f
где используются следующие морфизмы:
f: A → B, g: B → C и h: C → D
Все 3 композиции обозначают одно и то же: A опосредованно знает D.
Вам намекнули, что "A опосредованно знает D" — это уже не ассоциативность, а транзитивность, которая вообще не про скобки. А вот что Вы подразумеваете под отношением "знает" и как его транзитивность следует из ассоциативности композиции функций или наоборот — это уже загадка.
На рисунке ниже нарисованы 4 человека (или их страницы вконтакте — не суть важно): Иван, Я, Мария, Алёна. Пётр нас в данный момент не интересует.
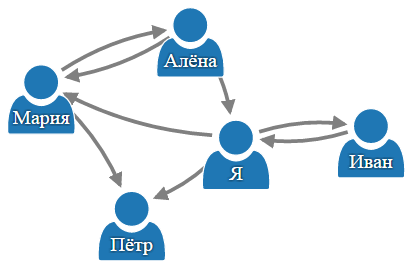
Пусть этот гипотетический Иван знает меня, неважно, в реальной жизни или в сети. Т.е. под отношением «знает» я подразумеваю именно то, что один человек знает другого. Пусть Я знаю гипотетическую Марию. Причём, если речь идёт, скажем, о теннисистке Марии Шараповой, то, скорее всего, она меня не знает, поэтому морфизм от неё ко мне не рисуем. Пусть Мария знает некоторую Алёну — рисуем ещё один морфизм.
Итого получается цепочка: Иван знает меня, Я знаю Марию, Мария знает Алёну.
При этом Иван опосредованно знает Марию через меня. Также Иван опосредованно знает Алёну через меня и Марию. Я опосредованно знаю Алёну через Марию. В отношение «опосредованно знает» я не вкладываю какой-то больший смысл, на интуитивном уровне это отношение вполне понятно: один человек знает кого-то, кто знает другого человека. Хотя, блин, я согласен, что в реальной жизни отношение «опосредованно знает» не используется и какое-то не очень интуитивное.
Будем считать, что в нашем примере один человек знает другого именно в реальности. Пусть я видел Марию Шарапову не только по телевизору, но, скажем, брал у неё автограф и жал ей руку. А, вот, Ивану так не посчастливилось. Но он может тешить себя тем, что знает Марию через два рукопожатия, а Алёну — через три.
Транзитивность отношения «опосредованно знает» нас в данном случае совершенно не интересует, поэтому я и не говорил о ней в статье. Для нас важно то, что следующие высказывания
«Иван через меня знает Марию, которая знает Алёну.»
«Иван знает меня, который через Марию знает Алёну.»
обозначают одно и то же:
«Иван через меня и Марию знает Алёну.»
Т.е. в этой цепочке «знания» можно группировать морфизмы (расставлять скобки) как угодно — всё-равно результат будет один.
Свободная категория, на мой взгляд, существенно сложнее категории множеств. Этот пример я привёл просто для затравки. Совсем серьёзно свободные категории мы в этом цикле скорее всего не будем рассматривать. И у более простых категорий есть интересные применения.
Почему не использовать синтаксис es6? Код сократился бы раза в 2.
И через typeof тип проверять не стоит:
function A() {}
class B {}
let a = new A();
let b = new B();
typeof a; // => "object"
typeof b; // => "object"Изначально не использовал ES6, потому что писал всё это преимущественно в 2013-ом году. Сейчас не стал переписывать, потому что по хорошему надо всё это разложить по модулям и существенно иначе организовать код. Но сейчас этим заниматься слишком рано, пока не реализованы более сложные категории.
С другой стороны, в том же d3.js не используются лямбды, классы и т.п. Разве что только модули. В общем, я согласен, что стоит переписать на ES6, но хочется поднакопить ещё категорий и сразу переписать нормально.
хочется поднакопить ещё категорий и сразу переписать нормально.
Раз так, очень советую писать на Typescript. Типы там конечно только во время компиляции живут (после компиляции всё становится обычным JS с его правилами), но, тем не менее, плюсов у TS намного больше, чем минусов, и его изучение окупится. Вот, например, доки с продвинутым использованием типов. Там и дженерики, и объединения типов, и другие плюшки.
Мне, как и разработчикам ES6 или TypeScript, не нравились некоторые особенности JavaScript. Но я планировал усовершенствовать JavaScript не просто добавлением статической типизации или коллекций, а созданием некоего CategoricalScript, основанного на теории категорий. На начальном этапе он может быть реализован просто в виде набора функций, написанных, на JavaScript. В будущем для него может быть запилен какой-то специальный синтаксис, но это не принципиально.
Например, язык Charity (ещё тут и тут) полностью основан на теории категорий. На мой взгляд, это качественно новый уровень по сравнению с остальными языками программирования.
Короче, эта библиотечка решает задачи аналогичные тем, которые решает TypeScript и т.п., но качественно иначе. Как именно она реализована уже вторично. Изначально хотелось сократить количество лишних прослоек в виде TypeScript и т.п., но в будущем будет виднее.
Уже ведь есть PureScript.
Да, он по мотивам Haskell. Насчёт "мало ТК в Haskell" у меня возникает вопрос: Вы хотите много теории категорий в языке, чтобы что? Какой-то практический смысл в этом будет? Или просто just for fun эзотерический ЯП создать?
В Haskell реализована одна категория Hask, в которой объекты — типы, морфизмы — функции. А, скажем, категория множеств или графов в нём из коробки не реализованы. Они нам понадобятся в следующих статьях для написания одного приложения. Мне мало осознания того, что, например, полиморфные функции в Haskell — это типа естественные преобразования и т.п. Всё-равно они остаются полиморфными функциями. А я хочу собрать какое-то осмысленное приложение полностью в терминах ТК. Чтобы в нём не было функций, классов, типов, а были только категории, функторы и т.п., чтобы все задачи на унификацию чего-то были описаны как коуравнители или кодекартовы квадраты в некоторой категории, чтобы все задачи на поиск оптимальной структуры описывались через универсальные свойства и т.п. Иными словами, хочу, чтобы не просто какие-то конструкции ЯП можно было бы описать в терминах ТК, а чтобы само приложение было написано в терминах ТК. Короче, в Haskell есть конструкции, которые типа из ТК, но всё-равно приложения пишутся в терминах функций, типов, классов, а не ТК.
Если получится всё приложение разложить на категории, пределы, универсальные свойства и т.п., то можно попробовать запилить под это ЯП, в котором уже не будет типов, функций, классов, а будут только категории, пределы,… Все привыкли к тому, что в ЯП есть функции, типы. А я хочу сделать ЯП, в котором будет что-то принципиально другое.
Не факт, что это получится, пока просто пишем приложение, о котором расскажу в следующих статьях, и разбираемся в ТК.
хочу, чтобы не просто какие-то конструкции ЯП можно было бы описать в терминах ТК, а чтобы само приложение было написано в терминах ТК. Короче, в Haskell есть конструкции, которые типа из ТК, но всё-равно приложения пишутся в терминах функций, типов, классов, а не ТК.
Для меня это выглядит логичным, потому что программисты, может быть за редким исключением, не мыслят в терминах теории категорий при разработке программы.
Но в любом случае, успехов Вам, может правда кому-то пригодится и такой ЯП.
Я вот за что математику люблю. За то, что если удалось какую-то человечески-сформулированную задачу поставить на математическом языке, то путем применения лемм, теорем и следствий мы имеем ответ (сначала на математическом, а затем и уже на человеческо-сформулированном).
Вот чувствую же что с теорией категорий можно всё, но без человеческой задачи сложно весьма. Вот смотрите, из практики. Есть множество товаров. «Морфизм» (?) для товаров — взаимодополняющие. Это категория, так как ассоциативна, и будем полагать что товар сам себя дополняет. Что можно из этого «заиметь бесплатно» с теорией категорий в руках?..
Что касается категории товаров. Можно каждый товар рассматривать как отдельный объект и мы получим свободную категорию. Но не уверен, что это удачный взгляд. С другой стороны, можно рассматривать категорию товаров как категорию отношений. Например, в этой категории будет объект { Автомобиль, Шина, Бензин, Силикон (для чернения шин), Телефон, Планшет, Внешний аккумулятор } и эндоморфизм на этом объекте, который является следующим отношением: { (Автомобиль, Шина), (Шина, Силикон), (Автомобиль, Бензин), (Телефон, Аккумулятор), (Планшет, Аккумулятор) }.
Причем, повторюсь, что такая категория будет именно категорией отношений, а не множеств. Потому что приведенный морфизм является отношением, а не функцией — он сопоставляет автомобилю два значения: шина и бензин.
Что делать с этой категорией дальше — я не знаю :) У меня есть практический пример использования теории категорий, я планирую его описать в одной из следующих статей, но он немного из другой области.
И вот лично что я увидел увидел в теории категорий, так это потенциал к AI-вычислениям, например, не так давно я баловался с F# и генетическими алгоритмами поиска действий, переводящих систему из точки А в точку В. Но генетические алгоритмы ненадежны, сами понимаете, random — а ему особо не доверишь чувствительные вопросы, даже на моих простецких модельках результаты зависели «от погоды на Марсе» — от тупо запуска программы. Так вот… теория категорий… оно ж решает уравнения. Уравнения относительно произвольных объектов, а объектом могут быть и математические, и любые другие операции. Вобщем задали вы мне материал для размышлений, даже как отвлекаться на обычную работу теперь не знаю :)
Сидел весь вечер с двумя примерами: дерево KPI предприятия и действия, условно, какой-нибудь единицы на поле боя. Если вершина, так выражусь, теории категорий — это уравнители, то никакой особо полезной информации, кроме того что «могут существовать эквивалентные порядки», мы похоже не получаем.
Возвращаясь к нашим товарам, можно размножить сущности на уровень ниже: у товаров есть свойства. Соответственно, операция «товар дополняет» должна сохранять какие-то соотношения у свойств. Наличие уравнителя бы означало бы, что, ну нет, не масло масляное, но близко к тому — «удочки хорошо идут с джипами». Вроде хорошо, только беда что утверждение имеет место с точностью до изоморфизма, коих может быть более чем континуально (ну не на конечном множестве естественно, а на конечных там всё вырождается в тривиальщину — в случае с KPI, а в случае с каким-нибудь танком — там бесконечность решений).
Хотя может я и неправильно всё рассудил.

Раз уж пишу ответом на свой бестолковый коммент чуть более чем полугодовалой давности, кое-что скажу и по поводу своих примеров.
Дерево KPI. Имеем несколько множеств индикаторов. Пусть каждое множество отражает некоторый аспект (без кавычек, в менеджменте это и есть аспекты, финансовый, рыночный, внутрикорпоративно-персональный, и другие). Морфизм — «показатель влияет». Навскидку, уравнитель даст множество «корневых» индикаторов — тех, которые определяют поведение всей системы.
Поле боя. Пусть есть множества боевых единиц двух враждующих сторон (разных родов войск). Морфизм — «может подбить». Аналогично, предел — множество единиц, которые всех могут подбить.
Что касается «AI и прочих умных и красивых обезьянок». Теория категорий в изложенном виде как мне видится может быть чертовски полезна в анализе (кластеризованных) событий с морфизмом «является причиной».
Ну вобщем захотелось написать свой теор-велосипед :) Спасибо еще раз за статью!
До категории Клейсли я дойду наверное не очень скоро. Ей везде уделяют очень много внимания. А более простые и, на мой взгляд, важные вещи (типа глобальных и обобщённых элементов) обходят стороной или рассматривают вскользь.
«она помогает правильно организовывать код, правильно называть классы и функции.»- да, ладно. Вы вкладываете в смысл организация кода явно не структуру файлов, каталогов и тд.
и про название классов и функций тоже мимо.
«Во-вторых, теория категорий позволяет писать универсальные алгоритмы» — универсальные для чего? Может он один универсальный алгоритм-то… Или если он не один, то почему они все универсальные…
Практического приложения не хватает очень…
Практическое приложение планируется в самой последней статье цикла.
Самая простая абстракция — это переход от «двух яблок», «двух камней» и т. д. к понятию числа 2; переход от «я повернулся боком», «камень повернулся боком» к понятию поворота на 90°. При этом манипулирование предметами заменяется на универсальные законы работы с числами (или с преобразованиями, или с чем-то еще).
Абстракция следующего уровня возникает, когда понимаешь, что правила обращения с числами 2, 3, 15 и т. д. по сути одинаковы. Все эти числа можно складывать, перемножать, для них работают переместительный, сочетательный и другие законы. Иными словами, все целые числа «играют по одним правилам». Поэтому часто полезно оперировать не с конкретными числами, а с новым математическим объектом — кольцом целых чисел. Аналогично, разные повороты предмета в пространстве являются элементами нового математического объекта — группы трехмерных вращений.
Третий уровень абстракции — это когда исчезает «осязаемость» элементов групп, колец, полей. Тут уже рассматриваются не конкретные группы вращений или иных преобразований, а просто абстрактные группы — совокупности элементов со строго очерченными свойствами. Здесь на первый план выходит то, какова структура группы, а не то, из чего она «состоит». Свойства всевозможных непротиворечивых математических структур, безотносительно к тому, где именно эти структуры возникают, изучает абстрактная алгебра.
Теория категорий предлагает подняться еще выше, на четвертый уровень абстракции. В ней изучаются уже не конкретные группы, а сеть математических взаимосвязей между разными группами. Аналогично, изучается сеть взаимосвязей между самыми разными типами пространств или между самыми разными кольцами. Более того, оказывается, что эти сети взаимосвязей (групп, полей, пространств и т. д.) — очень шаблонны. Между ними (между сетями!) можно установить параллели, и с помощью этих параллелей высокого уровня иногда удается решить очень трудные, но вполне конкретные задачи.
При этом, не будучи Георгием Перельманом...
Видимо, имеется ввиду Григорий Перельман.
Получается, что в категории множеств класс объектов и класс морфизмов совпадают? По крайней мере, с точностью до изоморфизмов. Интересно, есть ли какое-то строгое описание всего этого. Это похоже на какой-то частный случай леммы Йонеды или непонятно что.
Получается, что в категории множеств класс объектов и класс морфизмов совпадают? По крайней мере, с точностью до изоморфизмов
Именно что с точностью до изоморфизма, то есть сами классы не совпадают. А морфизмы нужны, чтобы композицию из них делать, и тут мы нужную для этого информацию безнадежно теряем. Как сюда Ионеду воткнуть, тоже не очень видно, потому что там все про hom-множества, а не про их отдельные элементы. Может и можно как-то проинтерпретировать, при желании.
Дело в том, что в данных категориях от некоторого объекта A к некоторому объекту B может идти максимум один морфизм.
Получается, что нет.
Соответственно, на языке теории категорий декартиан — это просто произведение объектов в категории множеств, а булениан — это, скорее всего, экспоненциал в категории множеств. Наверное для разных видов ступеней можно попробовать нарисовать коммутативные диаграммы, попробовать соотнести универсальные свойства произведений и экспоненциалов с каким-то «физическим» смыслом, который стоит за разными видами ступеней. Чтобы ответить что-то более конкретное, нужно лучше понять какой «физический» смысл стоит за разнообразиями, комплексами разнообразий, отношениями, комплексами отношений. Я не смог найти примеры.
Теория категорий на JavaScript. Часть 1. Категория множеств