Серпинский — польский математик, в честь которого назвали улицу в Варшаве и кратер на Луне. Он стал известен благодаря своим работам по теории множеств, аксиоме выбора, континуум-гипотезе, теории чисел, теории функций и так далее. В этом материале мы остановились на треугольнике Серпинского. Рассказали, что он из себя представляет, как его построить и в каких областях можно применять.
Краткая биография Серпинского
Вацлав Серпинский родился 14 марта 1882 г. в Варшаве, которая в то время входила в состав Российской империи. В 22 года он поступил на физико-математический факультет Варшавского университета. После его окончания ему присвоили звание кандидата наук и наградили золотой медалью за работы по теории чисел.
В 1905 году Серпинский получил степень доктора математических наук в Ягеллонском университете в Кракове. Вскоре после этого его назначили адъюнкт-профессором того же университета. Он ввел в университетскую программу курс по теории множеств, впервые включив такую дисциплину в академическую программу. В 1910 году Серпинского назначили профессором.
Одновременно с преподаванием он опубликовал несколько своих научных работ. Во время Первой мировой войны обстоятельства вынудили его остаться в России. Однако в 1918 году он смог вернуться в Польшу через Финляндию и Швецию. После возвращения Серпинского назначили заведующим кафедрой математики Варшавского университета, которую он занимал до конца своей карьеры.
Вклад ученого в науку
Теория чисел
В 1906 году Серпинский получил степень кандидата наук в Варшавском университете за свои работы в области теории чисел. Одним из его ранних научных трудов была статья «О разложении простых чисел в квадратичные формы», опубликованная в 1908 году. В ней он исследовал разложение простых чисел в квадратичные формы и применил алгебраические методы к арифметическим задачам.
Теория множеств и аксиома выбора
В 1917 году Серпинский опубликовал работу «Сведения о множествах, дополняющих кривую Пеано», в которой представил исследования в области теории множеств и предложил новый подход к изучению дополняющих множеств. Важным вкладом в теорию множеств стала его работа «Множество Кантора и аналогичные ему множества», опубликованная в 1920 году.
Фрактальная геометрия
В 1917 году Серпинский впервые упомянул о треугольнике Серпинского в работе «Сведения о множествах, дополняющих кривую Пеано». В 1920 году он опубликовал работу «Множество Кантора и аналогичные ему множества», в которой впервые упоминается о ковре Серпинского. Он активно исследовал фракталы в последующие годы и создал множество фрактальных конструкций, таких как квадратный фрактал и множество «серпинскомтине».
Что такое треугольник Серпинского
Треугольник Серпинского — это фрактал, который получается из треугольника путем рекурсивного деления его на меньшие треугольники. На каждом шаге берется каждый треугольник и заменяется на еще три равносторонних треугольника меньшего размера. Этот процесс повторяется до бесконечности для каждого из меньших треугольников, которые остались.
Три способа, как построить треугольник
Геометрический способ
Самый простой способ построить треугольник Серпинского — это геометрический:
постройте равносторонний треугольник;
разделите его на четыре равносторонних треугольника и удалите тот, который находится в центре;
повторяйте те же действия с остальными треугольниками до бесконечности.

Результатом повторного выполнения одного и того же действия будет фрактал. Он будет выглядеть одинаково даже при увеличении изображения. Это узор, который повторяется внутри самого себя.
Давайте рассмотрим математические свойства этого фрактала. Если площадь первого треугольника — A, то, разделив треугольник на четыре части и сохранив только три из них, получим оставшуюся площадь:

если повторять те же действия снова и снова, каждый раз разделяя треугольники на четыре части и сохраняя только три из них, по n-му шагу мы получим следующую формулу.
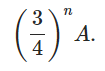
Это означает, что каждый шаг имеет меньшую площадь, чем предыдущий, и стремится к нулю, если продолжать до бесконечности.
Теперь, если периметр исходного треугольника равен, скажем, P, то на следующем шаге периметр заштрихованной области будет равен

поскольку мы должны добавить периметр вырезанного треугольника. Периметр растет на каждом шаге, и к n-му шагу он может быть выражен как

С каждым шагом площадь уменьшается и в конце концов достигает нуля, а периметр увеличивается и в конце концов становится бесконечным. Например, если мы начнем с треугольника с периметром всего 1 сантиметр, то после 62 повторений периметр заштрихованной области будет достаточно длинным, чтобы дотянуться от Земли до Луны и обратно.
Несмотря на это, все, что находится внутри этого треугольника, может поместиться на кончике пальца. На 62 шаге площадь заштрихованной области составит всего 3,45 х 10^-9 см^2. Это слишком мало для того, чтобы увидеть ее невооруженным глазом или отобразить на экране компьютера.
Треугольник Паскаля
Построить треугольник Серпинского-Паскаля можно с помощью следующих шагов:
начните с верхнего ряда треугольника и поставьте там число 1;
в следующем ряду под каждым числом поставьте 1, а между числами — сумму чисел, которые стоят над ними в верхнем ряду. Таким образом, во втором ряду будут стоять две единицы, а между ними число 2;
для всех остальных рядов сделаете то же самое;
продолжайте этот процесс для всех следующих рядов. Каждый новый ряд будет иметь на одно число больше, чем предыдущий.
Таким образом, получится пирамида чисел, где каждое число — это сумма двух чисел, стоящих над ним в верхнем ряду. Этот геометрическую фигуру называют «Треугольник Паскаля», его можно использовать для разложения многочлена (x + y)^k. Если в треугольнике есть достаточное количество рядов и мы выделим только нечетные числа, то обнаружим уже знакомый нам треугольник Серпинского.

Видение фрактального узора, подобного треугольнику Серпинского, в простой сетке четных и нечетных чисел, показывает, что связи между различными математическими темами могут быть обнаружены в самых неожиданных местах.
Мы получили треугольник Серпинского из треугольника Паскаля, когда взяли ряды и разделили числа на четные и нечетные, то есть разделили каждое число на 2 и сосредоточились только на остатках. Но что, если сосредоточиться на остатках и делить на другое число?
Если делить на число k и использовать разные цвета для каждого возможного остатка, то получится треугольник k-Серпинского. В следующей галерее представлен первый 641 ряд различных треугольников k-Серпинского.




В результате мы получаем обобщенную версию треугольника Серпинского. Теперь в треугольнике k-Серпинского можно увидеть все узоры, которые были скрыты в традиционном варианте, особенно если число k-простое.
Метод случайных точек
Чтобы построить треугольник методом случайных точек:
нарисуйте на листе бумаги три фиксированные точки A, B и C;
выберите начальную точку x0 где-либо на листе бумаги. Это будет точка, с которой начнется процесс построения треугольника;
выберите случайным образом одну из трех фиксированных точек A, B или C;
переместитесь из начальной точки x0 в среднюю точку выбранной фиксированной точки (A, B или C). Для выбранной точки A вычислите среднюю точку между x0 и A, для точки B — среднюю точку между x0 и B, для точки C — среднюю точку между x0 и C;
отметьте новую точку x1 в средней точке выбранной фиксированной точки. Это станет следующей точкой в построении треугольника;
повторите процесс, выбирая на каждом шаге одну из трех фиксированных точек A, B или C и перемещаясь в среднюю точку между выбранной точкой и последней отмеченной точкой. Это создаст новую точку x2, затем x3 и так далее;
продолжайте процесс до тех пор, пока вы не получите желаемую степень детализации и треугольник полностью не сформируется.

Вначале трудно разглядеть возникающую закономерность, поскольку есть всего несколько точек, которые расположены как бы в случайном порядке. Однако если повторить процесс достаточное количество раз, то треугольник Серпинского начинает приобретать очертания, а точки A, B и C образуют его вершины

Если не только отметить точки x0, x1 и так далее, но и провести линию, которая соединяет каждые две последовательные точки, то в итоге получится фигура.
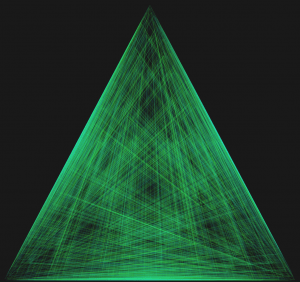
Если у нас есть точки A, B, C и D, и мы произвольно переместимся в среднюю точку любой из этих четырех точек, то в итоге получится треугольник Серпинского.
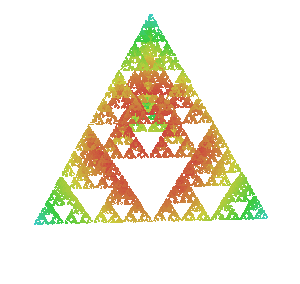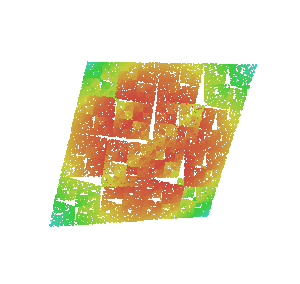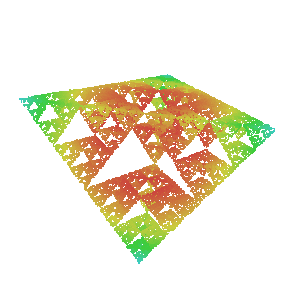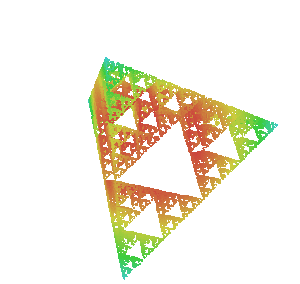
Можно даже выбрать k точек в пространстве размерности (k-1) и, произвольно перемещаясь к средним точкам, создать обобщенный фрактал Серпинского. Однако не получится визуально наблюдать этот фрактал, потому что мы не можем визуализировать такое количество измерений. Этот фрактал существует за пределами нашего визуального восприятия, но не за пределами нашего воображения.
Свойства треугольника Серпинского
Самоподобие. Каждая его более мелкая часть аналогична всему треугольнику в целом. Таким образом, он имеет степень самоподобия, и вся структура повторяется на все более мелких масштабах.
Фрактальность. Треугольник Серпинского — это фрактал, что означает, что он обладает сложной и повторяющейся структурой на всех уровнях масштаба.
Бесконечность. Процесс рекурсивного деления треугольника повторяется до бесконечности, что приводит к бесконечному числу мелких треугольников в структуре.
Плотность. Треугольник заполняет все пространство внутри исходного треугольника, но при этом имеет конечную площадь, так как его размер уменьшается с каждой итерацией.
Равносторонность. Исходный треугольник и все его более мелкие части — это равносторонние треугольники, у которых все стороны равны между собой.
Определенность. Каждый шаг рекурсивного деления строго определен и повторяется одинаково для каждого треугольника на всех уровнях масштаба.
Простота правил. Для получения треугольника применяется простое правило деления каждого треугольника на три равносторонних меньших треугольника без изменения углов и формы.
Сферы применения треугольника Серпинского
Треугольник Серпинского находит применение в различных областях.
Компьютерная графика и анимация. Треугольник Серпинского используют для создания узоров и текстур, а также для генерации фрактальных ландшафтов и фоновых изображений в компьютерной графике и анимации.
Алгоритмы и кодирование данных. Принцип самоподобия применяют в алгоритмах сжатия данных и кодировании, что может привести к более эффективному хранению и передаче информации.
телекоммуникации. Фрактальные антенны, основанные на принципе самоподобия, используют для повышения производительности и уменьшения размеров антенн в радиотехнике и мобильных связях;
Электроника и микроэлектроника. Треугольник Серпинского используют в дизайне интегральных микросхем для создания более эффективных и надежных структур.
Музыка и звуковые эффекты. Идея самоподобия фрактала применяют для создания уникальных музыкальных композиций и звуковых эффектов.
Образование и популяризация науки. Треугольник Серпинского используют для образовательных целей, чтобы познакомить людей с концепцией фракталов и помочь им понять абстрактные геометрические концепции.
Искусство и дизайн. Фрактальные узоры используют в искусстве и дизайне для создания уникальных узоров и композиций.
Треугольник Серпинского — захватывающая исследовательская тема
Треугольник Серпинского — это фрактал с удивительными свойствами самоподобия и фрактальности. Методы его построения открывают множество возможностей для исследования сложных геометрических структур и создания визуальных узоров. Ученые со всего мира продолжают и сейчас изучать треугольник Серпинского, так как фракталы остаются одной из активно разрабатываемых тем в области математики и компьютерных наук.