Мы снисходительно относимся к такому инструменту, как логарифмическая линейка. Однако она верой и правдой служила инженерам и конструкторам в течение долгого времени. С помощью этой самой линейки были созданы Ту-104 и первые космические ракеты. Но сейчас разработки таких масштабов нельзя представить без помощи компьютера.
В этой статье для блога ЛАНИТ я попытаюсь представить ретроспективу развития вычислительных приборов.

В технических вузах в 50-60 годах прошлого века в течение семестра преподавали специальный курс, который давал возможность освоить многочисленные нюансы использования логарифмической линейки.
Многие сейчас будут удивлены, но с ее помощью можно умножать, делить, определять площадь круга, находить квадраты и кубы чисел, логарифмы, синусы и тангенсы углов, переводить значения углов в радианы, причём со скоростью, не уступающей современным калькуляторам (рис. 1).

Операции сложения и вычитания на ней проводить было нельзя. Другой недостаток логарифмической линейки ― необходимость определять характеристику числа, а не только его мантиссу. Проще говоря, надо было подумать, где поставить запятую при определении порядка числа. Лично я не считаю это недостатком. Требовалось включить мозги, чтобы не заехать ненароком в макро- или микромир. Сейчас, используя калькулятор, мы сразу получаем число с известным порядком, безусловно доверяем ему. Однако во многих случаях необходимость осмысления полученного порядка расчета помогает шире посмотреть на решаемую проблему. С калькулятором теряется перспектива развития мыслительных возможностей нашего мозга. Попросите сегодняшнего школьника прикинуть, сколько стоит 330 г колбасы по цене 750 рублей за килограмм. Он обязательно полезет в калькулятор, хотя вполне достаточно поделить 750 рублей на три (с точностью до одного рубля).
Наиболее распространенный тип логарифмической линейки имеет длину 25 см, что позволяет получить результат расчёта с точностью до трёх знаков. Возник конфликт между длиной и точностью: чем линейка длиннее, тем она точнее, но тогда страдает компактность. В ограниченных экземплярах выпускали полуметровые и даже метровые линейки, печатали даже шкалы для самостоятельного изготовления линеек различной длины, а также создали круглые линейки (это уже не линейки, а «круглейки»), но они не получили большого распространения. Однако ими пользовались специалисты, которым необходима была компактность, например, геологи (рис. 2).

Операции сложения и вычитания механизировали с помощью арифмометров (от греч. αριθμός — «число», «счёт» и греч. μέτρον — «мера», «измеритель»), созданных на рубеже 19-20 веков. Распространённый в нашей стране арифмометр «Феликс» (рис. 3) в 1956 году стоил 110 рублей (примерно 12 тысяч по нынешнему курсу).

Самый маленький механический арифмометр Curta (высота 85 мм, диаметр 53 мм) использовали не только финансисты, но даже лётчики гражданских авиалиний, которые высчитывали на нём центровку и топливо.
При работе на арифмометре порядок действий всегда задаётся вручную — непосредственно перед каждой операцией следует нажать соответствующую клавишу или повернуть соответствующий рычаг. На арифмометре «Феликс» ввод чисел осуществляется перемещением рычажков вверх-вниз. Операция сложения требует оттягивания расположенной справа ручки и проворачивания её на один оборот от себя. Операция вычитания наоборот ― проворачивания на один оборот на себя. Умножение и деление реализовано как последовательные сложение и вычитание при перемещении каретки на один шаг для перехода на следующий или предыдущий порядок (при делении).
Потребность в ускорении расчетов породила электромеханические арифмометры, представители которых показаны ниже (рис. 4). Старшее поколение помнит, что определить местоположение бухгалтерии предприятия можно было по страшному грохоту, который производили эти вычислительные машины. Но им было по силам умножение и деление уже без ручного перевода разрядов. Разновидностью этого вида устройств являлись электромеханические кассовые аппараты, которые осуществляли ввод денежной суммы, номера секции магазина и чека (машина была снабжена автоматическим четырёхзначным нумератором), а также ввод даты выдачи чека (ежедневно выставлялся вручную), фиксированной дополнительной информации (например, названия предприятия или номера кассы). Машины такого типа выпускались в больших количествах, но сохранились немногие, так как их списание контролируется законом.

С конца 70-х годов началась эра электронных калькуляторов и вычислительных машин. Производить расчёты стало просто, быстро и в какой-то мере неинтересно с точки зрения получения удовольствия от самих вычислений (слишком быстро получаются). Зато появилась возможность оперативно выполнить расчеты, на которые раньше требовались годы.
Появление персональных компьютеров стимулировало громадный скачок в развитии вычислительных возможностей. Если в 70-х годах прошлого века учебное пособие Копченова Н.В., Марон И.А. «Вычислительная математика в примерах и задачах» (Наука, 1972) рекомендовало для решения дифференциальных уравнений прикладных задач использовать так называемый метод сеток, связанный с весьма громоздкими ручными вычислениями, то в настоящее время это весьма просто и изящно выполняется с помощью Excel с получением в результате математической модели.
Привожу пример расчёта изменения концентрации водорода в отливке сечением 200х200 мм в процессе ее остывания в литейной форме. В основу расчета положено решение дифференциального уравнения диффузии для двумерного случая, т.е. когда рассматривается распределение водорода в поперечном сечении отливки, если её длина не менее чем в пять раз больше её сечения. Уравнение диффузии для двумерного случая имеет следующий вид (Источник: Батунер Л.М., Позин М.Е. Математические методы в химической технике, Ленинград, «Химия», 1968):
Решением уравнения (1) является ряд вида:
– концентрация водорода в текущий момент времени
в точке с координатами
,
.
– шаг разбиения по координате
;
– шаг разбиения по координате
;
– размер отливки по координате
;
– размер по координате
.
Начальные условия: исходная концентрация водорода в металле отливки – .
Запись (3) означает, что в начальный момент времени концентрация водорода по сечению отливки равномерна и равна исходной концентрации ; по прошествии значительного промежутка времени концентрация водорода падает до нуля.
Граничные условия:
Запись (4) означает, что на поверхности отливки концентрация водорода принимается равной нулю в течение всего процесса дегазации.
Решение уравнения (1) с помощью ряда (2) сводится к вычислению концентрации в точках с координатами
для моментов интегрального времени:
– коэффициент диффузии
;
– температура
;
– время.
Значения коэффициента диффузии выбираются из следующих данных. Объектом расчета является конструкционная сталь Сr-Ni-Mo-композиции. При охлаждении в области температур от 1000 до 300 использована зависимость, известная для
(Гельд П.В., Рябов Р.А. Водород в металлах и сплавах, М., «Металлургия», 1974):
При охлаждении в области температур 300-20 использована зависимость, известная для
:
Расчет проводился в Excel с помощью подпрограммы, составленной на языке Delphy 5.0. Блок-схема подпрограммы приведена на рис. 5.
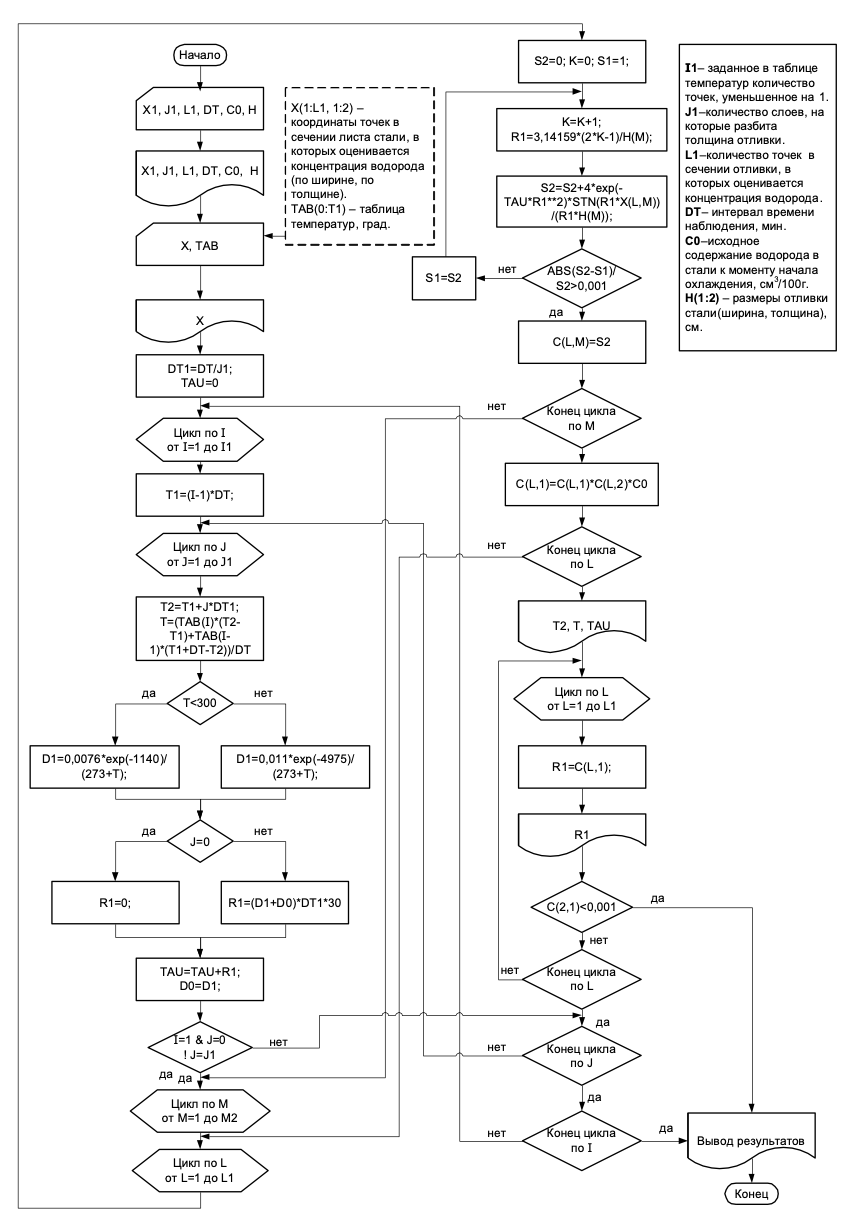
Результат расчёта, выведенный подпрограммой в Excel, представлен на рис. 6.
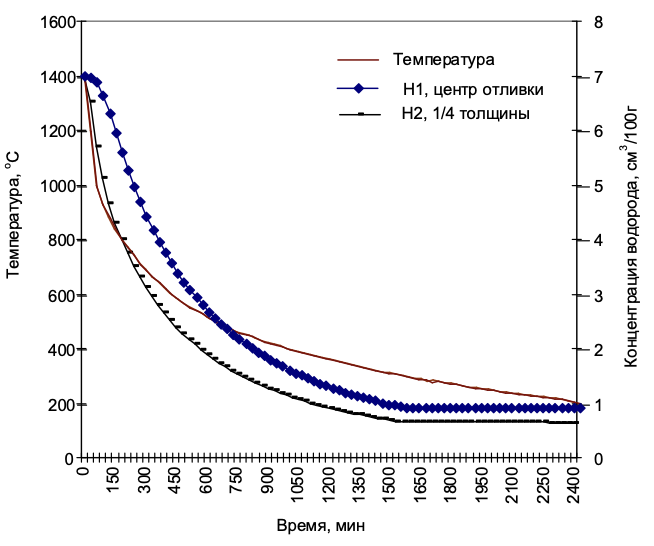
Приведенный расчет имеет прикладное значение. Он позволяет достоверно оценить конечное содержание водорода в отливке и принять решение о дальнейшей обработке, чтобы предотвратить дефекты водородного происхождения. Кроме того, составив один раз эту программу, можно выполнить бесконечное количество вариативных вычислений: изменить размеры и начальные условия, проверить влияние значений коэффициента диффузии. Другое практическое применение ― возможность рассчитать скорость изменения температуры при охлаждении и нагреве, так как дифференциальные уравнения диффузии и теплопроводности полностью идентичны. Например, можно определить температуру стенки дизеля или газотурбинного двигателя в процессе их эксплуатации в различных режимах, не прибегая к дорогостоящим натурным измерениям.
Инженерные вычисления производятся не для самих вычислений как таковых, а для расчёта инженерных конструкций, проектирование которых традиционно проводилось с помощью чертёжных инструментов, в частности, кульмана, который был неотъемлемым атрибутом инженера-конструктора и является таковым до настоящего времени (рис. 7).

Электронные вычислительные машины осуществили переворот в вычислительной технике. На рисунке показана одна из первых ламповых БЭСМ.

Персональные компьютеры дали импульс к появлению большого количества прикладных программ для систем автоматизированного проектирования (САПР, CAD – Computer Aided Design) типа AutoCad, Autodesk Inventor, SolidWorks, SolidEdge, Компас-3D, бесплатных программ – LibreCAD, QCAD, Bently View, Tinkercad, nanoCAD, OpenSCAD, BRL-CAD, ZBrush на платформах Windows, Linux, Mac, которые позволяют проектировать в двумерной и трехмерной среде, строить 3D-модели, создавать и оформлять чертежи непосредственно на экране компьютера.
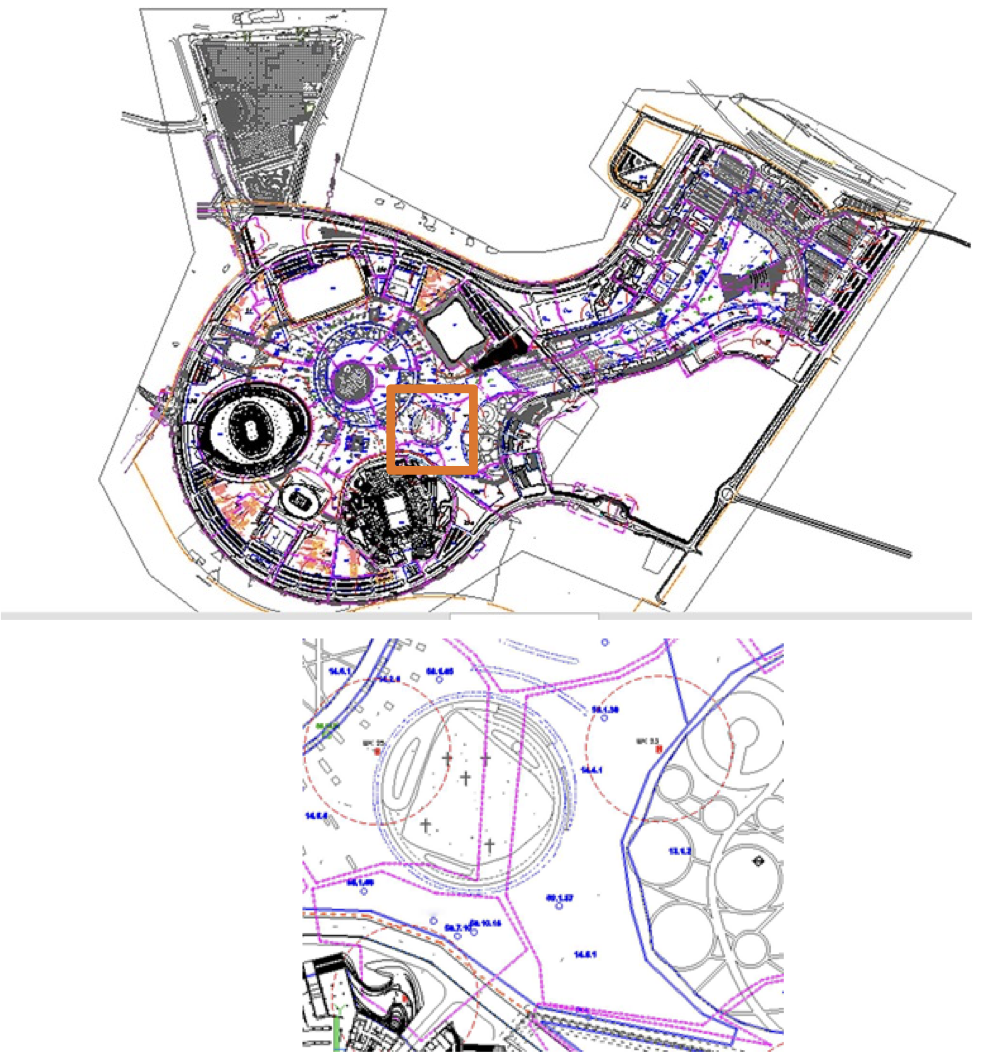
AutoCad (компания Autodesk) – самая распространённая CAD-система в мире. В ней можно выполнять строительные, машиностроительные проекты, работать с изысканиями, электрикой и др., осуществлять многоуровневую детализацию. На рис. 8 показан выполненный в AutoCad проект Олимпийского парка в Сочи и область подробной детализации размещения объектов, обозначенная красным квадратом.
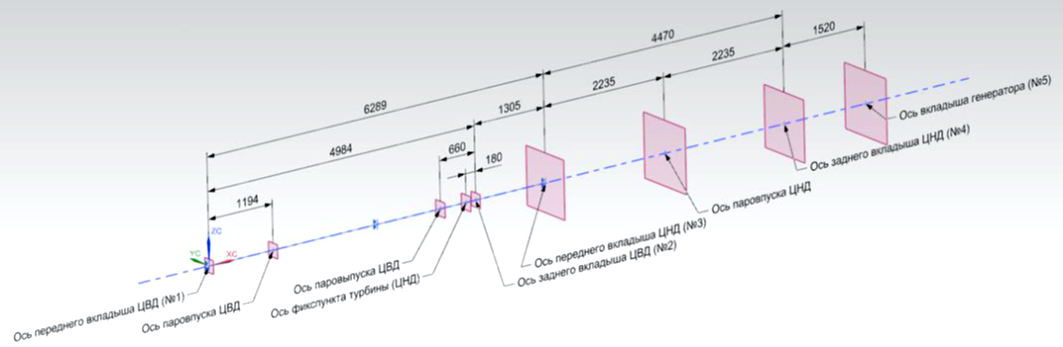
Конструкторское проектирование при использовании современных CAD-инструментов осуществляется по несколько другим принципам, чем традиционное последовательное вычерчивание деталей, узлов, агрегатов и изделия в целом. Сейчас проектирование начинается с формирования так называемой базовой контрольной структуры (БКС) – это сборка, содержащая информацию для проработки, согласования, утверждения и изменения информации о базовой геометрии основных составных частей изделия, их относительного пространственного положения и геометрических взаимосвязей между ними, начиная с ранних стадий жизненного цикла изделия. Компоненты верхнего уровня БКС создаются главным конструктором проекта сразу после получения технического задания, его анализа и выбора аналога (рис. 9).
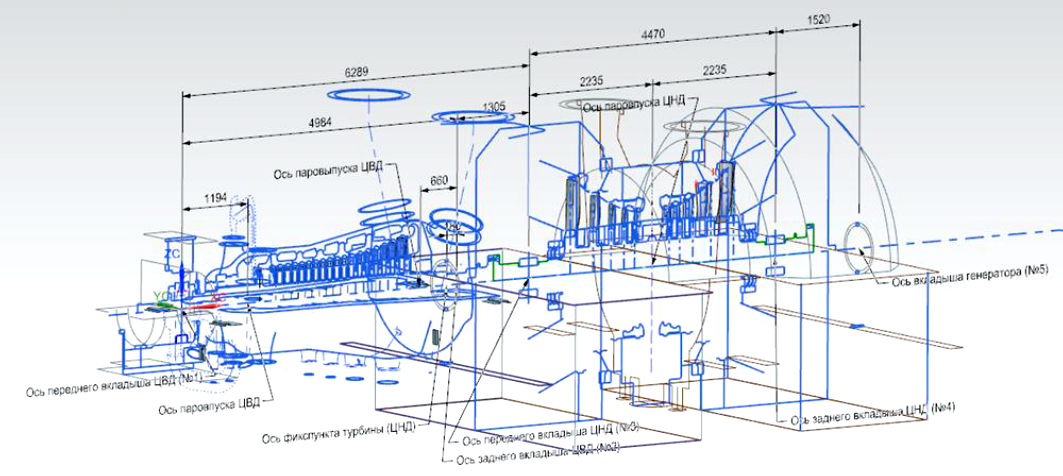
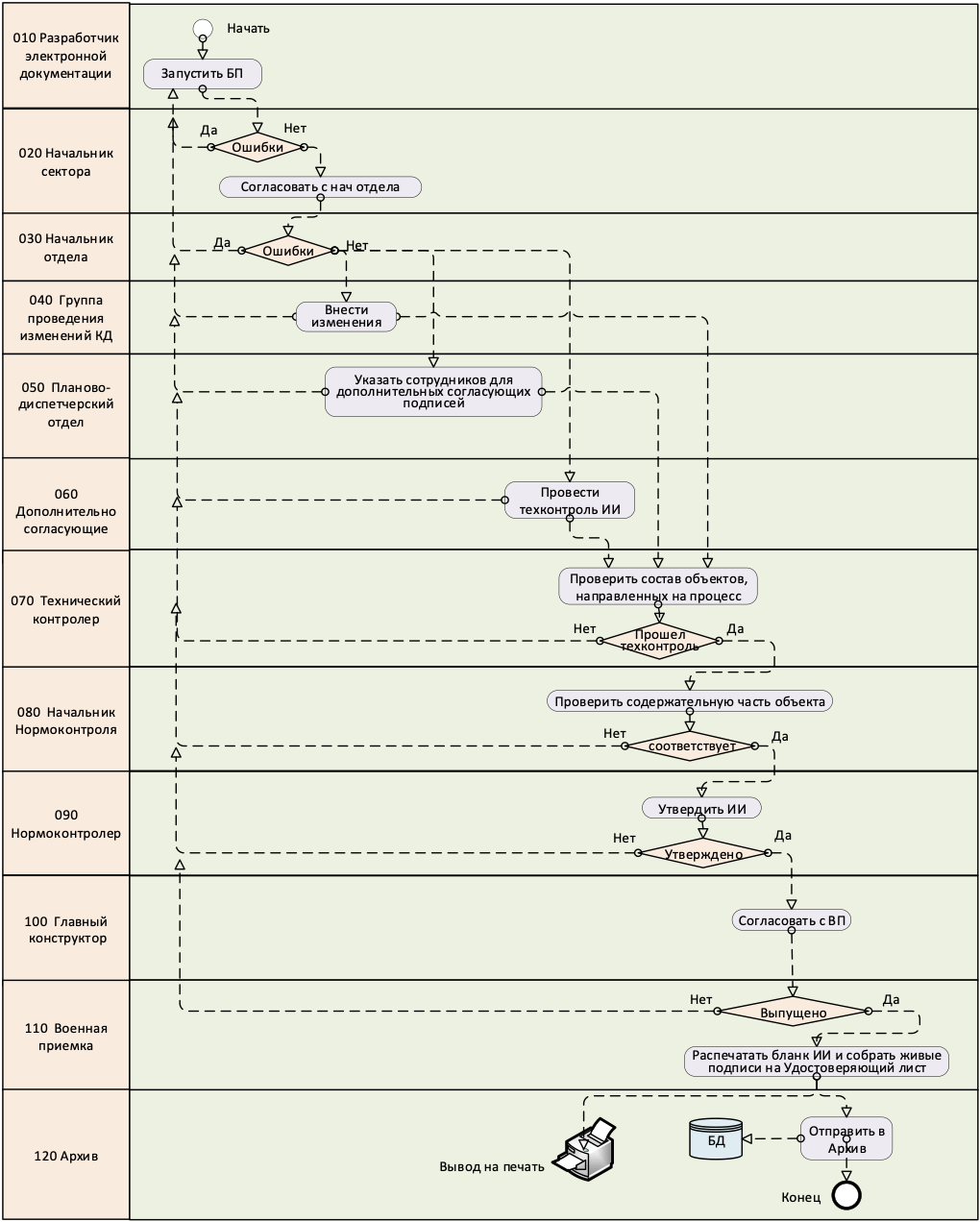
На основании согласованной БКС в дальнейшем производится проектирование отдельных узлов и деталей соответствующими подразделениями и формируется общий комплект конструкторской документации. На этом создание документации не заканчивается. На рис. 11 показаны стадии, предшествующие окончательному утверждению комплекта электронных чертежей. Чтобы облегчить и ускорить эту организационную и техническую работу, созданы компьютерные программы, в качестве одной из них можно назвать Teamcenter (c программой можно ознакомиться в книге Тороп Д. Н., Терликов В. В. Teamcenter. Начало работы, М.: ДМК Пресс, 2011). Программа позволяет не только проектировать, но и управлять проектами, инженерными процессами, расчётными и технологическими данными, взаимоотношениями с поставщиками, оформлять отчеты и аналитику.
Хочу обратить внимание, что компьютерное проектирование, которое начинается с базовой контрольной структуры, не является открытием, связанным именно с появлением компьютера. Просто создание БКС ранее происходило у конструктора в голове. Посмотрите на эскизы Сергея Павловича Королева и фотографию ракеты Р7, созданной под его руководством (рис. 12 и 13).


Резюме
Я попытался кратко описать развитие техники вычислений и инженерного проектирования. Но немного отвлекусь от восьмиядерных процессоров ноутбуков и попытаюсь изложить мысли, которые возникли у меня, когда я писал этот обзор.
30 лет назад в альпийском леднике случайно обнаружили мумифицированное тело человека, замершего 5300 лет назад. Возраст был точно установлен с помощью радиоуглеродного анализа. При нем нашли медный топор с тисовой рукояткой (очень редкая вещь для неолита), контейнер из бересты с запасом древесных углей, кремни, трут, бересту, то есть все необходимое для быстрого розжига костра. Человек, его условно назвали «Эци», по-видимому, был ранен, наконечник стрелы застрял у него в плече и, как предполагают, спасаясь от погони, он, вероятно, замерз на леднике. При нём нашли также каменный нож, тисовый 180-сантиметровый лук и стрелы. Дотошные исследователи изготовили несколько точных копий этого лука и определили, что по характеристикам он не уступает современным спортивным и мог уверенно поражать добычу на расстоянии до 80 м. То есть этот человек был прекрасно приспособлен к существованию в той среде, в которой он жил.
Мы тоже непрерывно приспосабливаемся к технической, интеллектуальной, информационной среде, в которой мы сейчас существуем. Эта способность приспособления есть удивительное свойство нашего мозга, и при этом наши тела и наш мозг постепенно и непрерывно изменяются, иногда избавляясь от ставших ненужными частей тела (как наши пращуры 15 млн лет назад избавились за ненадобностью от хвоста, которым цеплялись за ветки деревьев) и, к сожалению, от некоторых функций, которыми обладал наш мозг совсем недавно. К примеру, мало кто считает сейчас в уме. Зачем, если есть калькулятор? Может быть, если так дело пойдет дальше, мы и вовсе потеряем эту способность.
Вот еще один пример о наступлении цифрового мира в нашу жизнь. Студент РГГУ написал и защитил диплом с помощью нейросети ChatGPT, потратив на написание сутки, причем проверка на плагиат показала оригинальность 83 процента. Надо отдать должное умению студента использовать современные технологии, и хотя на защите он получил всего лишь трояк, не означает ли данный факт, что в недалеком будущем когнитивные функции человека может заменить что-то вроде продвинутого калькулятора, а способность творчески мыслить со временем атрофируется.
Непрерывно совершенствуя вычислительную и связанные с ней другие технологии, мы неизбежно будем терять некоторые свои способности, в том числе и функциональные мозговые. Технический прогресс остановить невозможно. Человек так устроен, что непрерывно совершенствует среду и совершенствуется сам. Значит, будут происходить изменения и в нём самом. Создание искусственного интеллекта, очевидно, приведёт к каким-то революционным изменениям нашего мозга. Он будет совершенствоваться так радикально, как мы не можем сейчас представить. Вследствие этого будет происходить взрывной прогресс технологий, масштабы и последствия которого также невозможно вообразить. Но при этом мы что-то и потеряем, как сейчас большинство из нас потеряли способность выживать в дикой природе (за исключением отдельных энтузиастов, которые, тем не менее, через месяц жизни на природе отмываются в ванне). Надо также помнить слова Курта Воннегута: «Над чем бы ученые ни работали, у них всё равно получается оружие».
Мне повезло в определённом отношении. В течение своей жизни я смог воочию проследить весь прогресс вычислительной техники от логарифмической линейки до ноутбука, но на все это ушло почти 70 лет, и, надеюсь, я не сильно отстал от молодого поколения в степени овладения информационными технологиями.
При этом я все-таки оптимистично настроен. Представьте, что современный годовалый ребенок попал в прошлое, к неандертальцам. Он вырастет и будет полноправным членом их сообщества, будет охотиться на мамонтов и не проявит интереса к освоению смартфона, потому что понятия не имеет, что это такое. Давайте еще пофантазируем и отправим того же младенца на 2000 лет в будущее. Он вырастет и будет пользоваться всеми благами того общества, которое его вырастило, не будет ничем особенным выделяться среди сверстников, хотя, вполне возможно, проявит какие-то выдающиеся способности в такой области, о существовании которой мы не подозреваем. Пластичность нашего мозга бесконечна, он может приспособиться ко всему.
Но есть одно НО. Пластичность теряется с возрастом. Нельзя стать виртуозным музыкантом, начав заниматься музыкой в 50 лет, хотя, возможно, и были подобные случаи (что только подтверждает мою мысль о безграничной пластичности мозга). Вывод тривиален – учись смолоду, учись всю жизнь.