Как быстро вычисляются логарифм и экспонента в компьютере?

[sepetov]

Не по теме статьи, но поделюсь рецептом как быстро прикинуть в уме десятичный логарифм. Как оказалось, это почему-то знают не все, хотя в какой-то мере даже интуитивно. Вдруг кому пригодится (pH посчитать, ну или *бару какую-нибудь).

Сразу примеры:

• lg(4567) = 3.6

• lg(78901234) = 7.9

• lg(44) = 2.6

Закономерность такая: целая часть - это количество цифр в числе минус один (=порядок числа). Дробная часть - это первая цифра числа плюс два. Почему-то (с).

Правило имеет исключение: если первая цифра числа - это единица или девятка, то двойку к дробной части не прибавляем, а к восьмёрке можно прибавить единицу. Например:

• lg(123) = 2.1, а не 2.3

• lg(98765) = 5.99, а не 6.1

Возможно, уже где-то на хабре и было.

[novoselov]

lg(4567) = 3.6596 (округление не сработало)

lg(78901234) = 7.8970 (округление сработало)

lg(44) = 1.6434 (алгоритм справился лучше автора)

lg(123) = 2.0899 (округление сработало)

lg(98765) = 4.9946 (это пять)

А объясняется все довольно просто

Hidden text

[sepetov]

В третьем и последнем пунктах, конечно, опечатался. Не из калькулятора же копировал.

В остальных, как видите, отличная точность с целью прикинуть точнее целых величин.

[Andy_U]

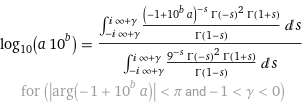
На самом деле, экспонента и возведение в степень вычисляются практически одинаково:

Вы бы заменили это странное утверждение на что-нибудь типа "Можно легко доказать, что:"