Здравствуйте, уважаемое хабрасообщество.
В последнее время на хабре стали появляться статьи, так или иначе связанные с анализом и обработкой сигналов и изображений (например Обнаружение устойчивых признаков изображения: метод SURF, Интегральное представление изображений от BigObfuscator), в связи с чем я хотел бы вкратце осветить такой инструмент для анализа сигналов, как wavelet-преобразование.
Для того, чтобы понять смысл вейвлет анализа начнем довольно издалека. В данной статье описывается математический смысл (простыми словами) вейвлет-преобразований, о применимости и его дискретной версии я расскажу позднее.
Спектральный анализ — это один из методов обработки сигналов, который позволяет характеризовать частотную составляющую измеряемого сигнала.
Главной математической основой спектрального анализа является преобразование Фурье, которое связывает пространственный или временной сигнал (либо некоторую модель этого сигнала) с его представлением в частотной области.
Преобразование Фурье функции f является интегральным представлением и задается следующей формулой:

Но преобразование Фурье дает информацию только про частоту, которая присутствует в сигнале и не дает никакой информации про то, в какой промежуток времени эта частота присутствует в сигнале.
Таким образом для следующего стационарного сигнала:
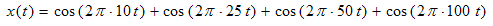
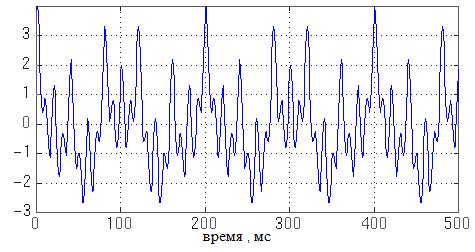
преобразование Фурье будет иметь вид:
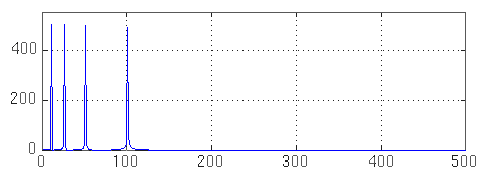
А для не стационарного сигнала:
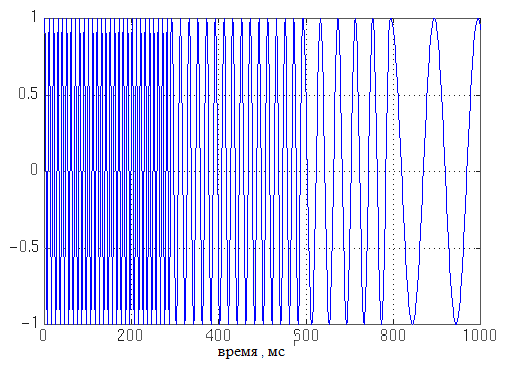
преобразование Фурье будет иметь вид:
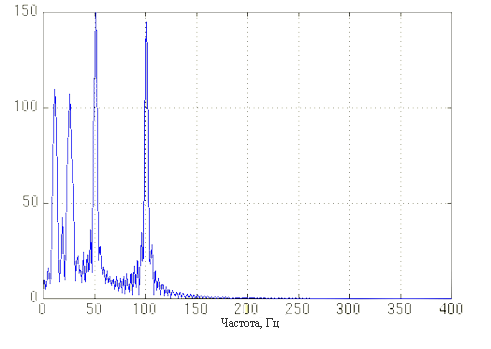
Таким образом, для двух абсолютно разных сигналов мы получаем почти одинаковые преобразования Фурье (не плавность графика преобразования Фурье для второго сигнала объясняется внезапной сменой частоты в этом сигнале, а разница в амплитуде разных частот объясняется тем, что эти частоты действовали на протяжении разного времени на рассматриваемом отрезке сигнала).
Таким образом преобразование Фурье по своей сути не может отличить стационарный сигнал от нестационарного, что является большой проблемой для его применимости.
Другим инструментом спектрального анализа является оконное преобразование Фурье (Short-time Fourier transform), которое является разновидностью преобразования Фурье и определяется следующим образом:
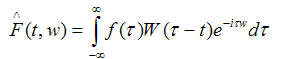
где W(Tau-t) — некоторая оконная функция.
Обычно в качестве оконной функции используется гауссиан, окно Хемминга, окно Ханна или окно Кайзера.
Оконное преобразования Фурье, в отличии от обычного преобразования Фурье, уже является функцией от времени, частоты и амплитуды. То есть она позволяет получать характеристику распределения частоты сигнала (с амплитудой) во времени.
Рассмотрим следующий не стационарный сигнал:
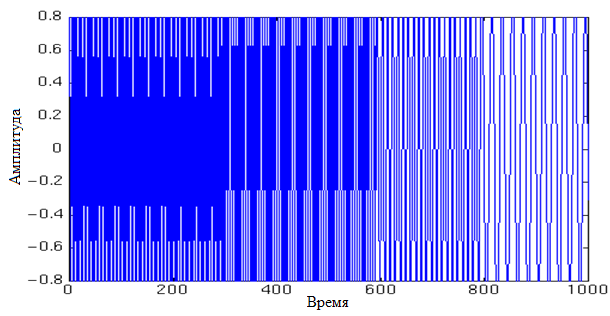
Этот сигнал является стационарный каждые 250мс (на первом отрезке длинной 250мс он имеет частоту 300Гц, на втором — 200Гц, на третьем — 100Гц и на четвертом — 50Гц).
Трехмерный (время, частота и амплитуда) график оконного преобразования Фурье будет иметь следующий вид:
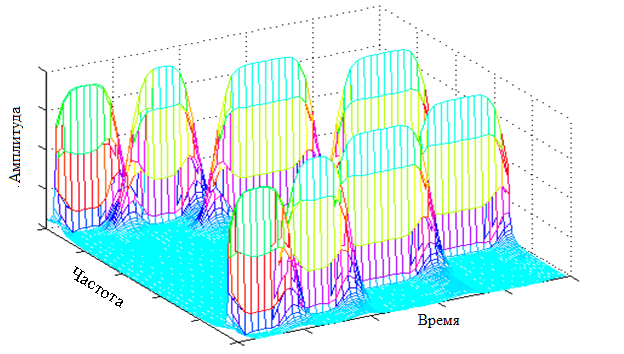
(симметричность графика объясняется тем, что преобразования Фурье (в том числе и оконное преобразования Фурье) являются симметричными для любого сигнала)
На этом графике мы можем увидеть четыре ярко выраженных максимума, которые соответствуют частотам, присутствующим в сигнале. Самым важным является то, что в отличии от обычного преобразования Фурье мы получаем значения частот относительно оси времени, то есть получаем частотно-временную характеристику сигнала.
Но главной проблемой в использовании оконного преобразования Фурье для получения частотно-временной характеристики сигнала является так называемый принцип неопределенности Гейзенберга, который возникает для параметров времени и частоты сигнала.
В основе принципа неопределенности лежит тот факт, что невозможно сказать точно какая частота присутствует в сигнале в данный момент времени (можно говорить только про диапазон частот) и не возможно сказать в какой точно момент времени частота присутствует в сигнале (можно говорить лишь про период времени).
В связи с этим возникает проблема разрешающей способности. Разрешающую способность оконного преобразования Фурье можно регулировать с помощью ширины окна.
Оконное преобразования Фурье с узким окном в форме Гауссиана с масштабом (обратная величина к ширине окна) 0.01 будет иметь следующий вид:
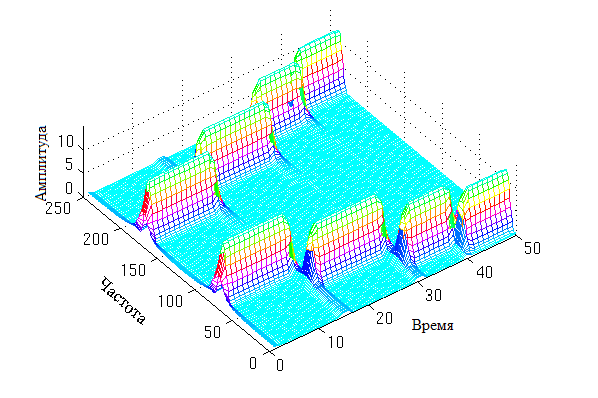
Как видно, полученное преобразование Фурье имеет хорошую точность относительно времени и плохую точностью относительно частоты (каждый максимум занимает некоторый диапазон частот).
При использовании более широкого окна в форме Гаусианна с масштабом 0.00001 оконное преобразование будет иметь вид:
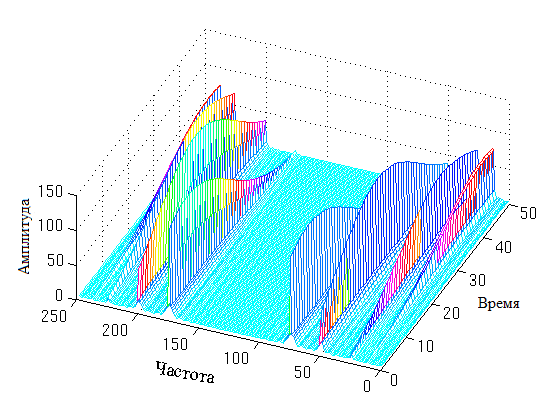
Видно, что в данном случае мы получаем высокую точность относительно частоты, но при этом очень низкую точность относительно времени.
Можно считать, что обычное преобразование Фурье является оконным преобразованием Фурье с окном шириной в бесконечность.
Таким образом при увеличении ширины окна (уменьшении его разрешающей способности) мы увеличиваем точность относительно частоты и уменьшаем точность относительно времени.
Какое тогда подобрать значение ширины окна, чтобы добиться оптимального соотношения точностей? На этот вопрос отвечает вейвлет-преобразование.
Вейвлет преобразование было создано как инструмент, который решает проблему неопределенности Гейзенберга для построение частотно-временных характеристик сигнала.
Вейвлет преобразование сигнала f(t) имеет вид:
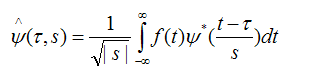
где Tau — сдвиг по времени, S — масштаб, а Psi* — материнский вейвлет.
Понятие вейвлета означает волну, которая проходит через сигнал и является окном некоторой ширины (масштаба) для некоторого местоположения во времени, во время (простите за тавтологию) интегрирования сигнала.
Материнский вейвлет — это функция, которая является прототипом для всех окон, которые будут генерироваться во время вейвлет-преобразования.
Сдвиг по времени регулирует движение генерированных окон по временной компоненте сигнала.
Понятие масштаба является обратным к понятию ширины окна. Чем меньше ширина окна, тем больше масштаб, то есть окно захватывает меньшую часть сигнала и сигнал интегрируется более «детально».
Чем больше ширина окна, тем меньший масштаб, то есть окно захватывает бОльшую часть сигнала и сигнал, соответственно, интегрируется менее «детально».
Опишем процесс вейвлет преобразования (в качестве материнского вейвлета используется гауиссиан) некоторого непрерывного сигнала, который действовал на протяжении некоторого промежутка времени (0-200мс) с нормализованной амплитудой (0-1):
1. Рассчитывается интеграл при начальных условиях Tau=0 и S=1;
а) увеличивается параметр Tau(i) =Tau(i-1)+e на некоторое достаточно малое число e и рассчитывается интеграл. Выполняется пока Tau(i) не станет равным 200мс (концу сигнала).
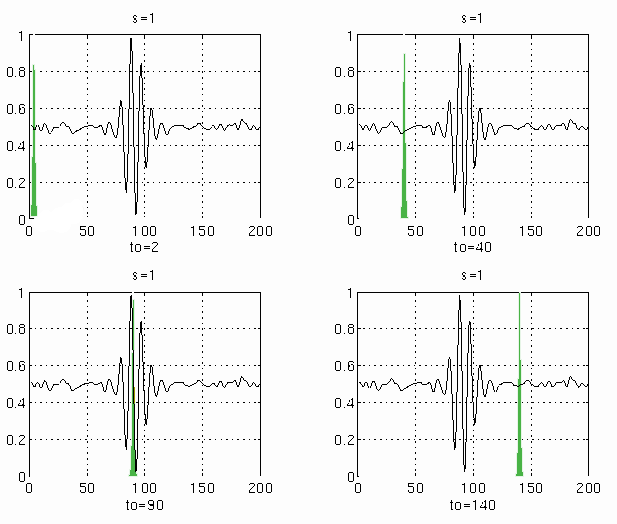
2. Изменяется параметр S=5, значение Tau опять устанавливается в начальную точку сигнала (Tau=0);
а) увеличивается параметр Tau(i)=Tau(i-1)+e на некоторое достаточно малое число е и рассчитывается интеграл. Выполняется пока Tau(i) не станет равным 200мс (концу сигнала).
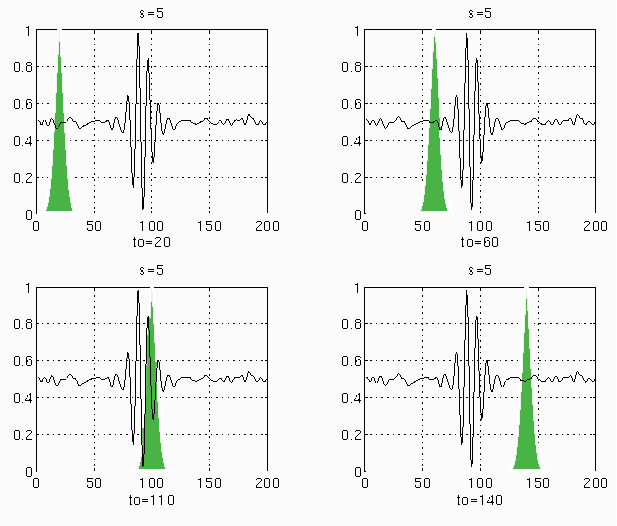
Аналогично рассчитываются интегралы для значений параметра S=20, S=50 и т.д.
В результате описанного процесса мы получаем рассчитанные значения интегралов функции для каждого масштаба в каждый момент времени.
Таким образом мы получаем трехмерное представление сигнала с компонентами: масштаб, время и амплитуда (значения рассчитанных интегралов).
Рассмотрим следующий не стационарный сигнал:
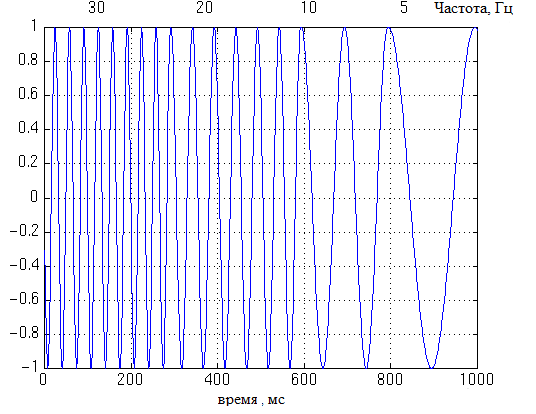
Вейвлет преобразования для такого сигнала будет иметь вид:
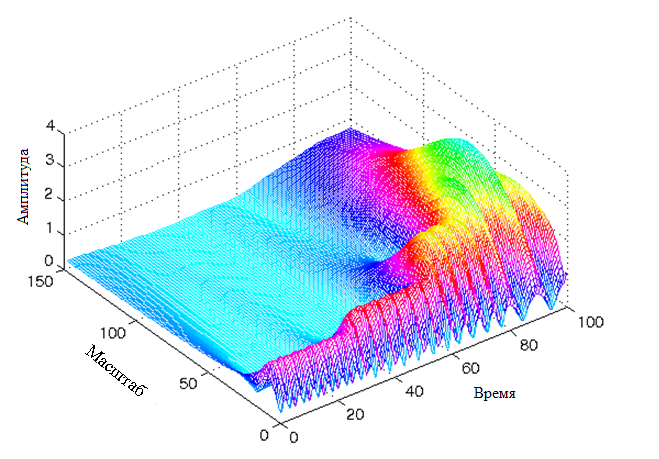
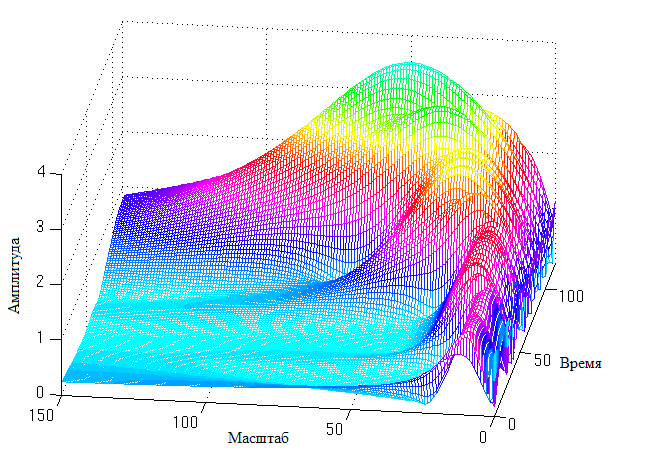
Таким образом, вейвлет-преобразования, в отличии от оконного преобразования Фурье, которое имеет постоянный масштаб в любой момент времени для всех частот, имеет лучшее представление времени и худшее представление частоты на низких частотах сигнала и лучшее представление частоты с худшим представлением времени на высоких частотах сигнала.
На рисунках хорошо видно, что полученное вейвлет-преобразование является более детализированным по времени в области высоких значений масштаба (низких частот) и менее детализирована в области низких значений масштаба (высоких частот).
Из этого следует, что вейвлет преобразования дает возможность уменьшить влияние принципа неопределенности Гейзенберга на полученном частотно-временном представлении сигнала. С его помощью низкие частоты имеют более детальное представление относительно времени, а высокие — относительно частоты.
Использованная литература: Wavelet-tutorial
В последнее время на хабре стали появляться статьи, так или иначе связанные с анализом и обработкой сигналов и изображений (например Обнаружение устойчивых признаков изображения: метод SURF, Интегральное представление изображений от BigObfuscator), в связи с чем я хотел бы вкратце осветить такой инструмент для анализа сигналов, как wavelet-преобразование.
Для того, чтобы понять смысл вейвлет анализа начнем довольно издалека. В данной статье описывается математический смысл (простыми словами) вейвлет-преобразований, о применимости и его дискретной версии я расскажу позднее.
Спектральный анализ — это один из методов обработки сигналов, который позволяет характеризовать частотную составляющую измеряемого сигнала.
Преобразование Фурье
Главной математической основой спектрального анализа является преобразование Фурье, которое связывает пространственный или временной сигнал (либо некоторую модель этого сигнала) с его представлением в частотной области.
Преобразование Фурье функции f является интегральным представлением и задается следующей формулой:

Но преобразование Фурье дает информацию только про частоту, которая присутствует в сигнале и не дает никакой информации про то, в какой промежуток времени эта частота присутствует в сигнале.
Таким образом для следующего стационарного сигнала:
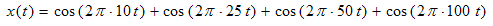

преобразование Фурье будет иметь вид:

А для не стационарного сигнала:

преобразование Фурье будет иметь вид:

Таким образом, для двух абсолютно разных сигналов мы получаем почти одинаковые преобразования Фурье (не плавность графика преобразования Фурье для второго сигнала объясняется внезапной сменой частоты в этом сигнале, а разница в амплитуде разных частот объясняется тем, что эти частоты действовали на протяжении разного времени на рассматриваемом отрезке сигнала).
Таким образом преобразование Фурье по своей сути не может отличить стационарный сигнал от нестационарного, что является большой проблемой для его применимости.
Оконное преобразование Фурье
Другим инструментом спектрального анализа является оконное преобразование Фурье (Short-time Fourier transform), которое является разновидностью преобразования Фурье и определяется следующим образом:
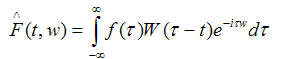
где W(Tau-t) — некоторая оконная функция.
Обычно в качестве оконной функции используется гауссиан, окно Хемминга, окно Ханна или окно Кайзера.
Оконное преобразования Фурье, в отличии от обычного преобразования Фурье, уже является функцией от времени, частоты и амплитуды. То есть она позволяет получать характеристику распределения частоты сигнала (с амплитудой) во времени.
Рассмотрим следующий не стационарный сигнал:

Этот сигнал является стационарный каждые 250мс (на первом отрезке длинной 250мс он имеет частоту 300Гц, на втором — 200Гц, на третьем — 100Гц и на четвертом — 50Гц).
Трехмерный (время, частота и амплитуда) график оконного преобразования Фурье будет иметь следующий вид:

(симметричность графика объясняется тем, что преобразования Фурье (в том числе и оконное преобразования Фурье) являются симметричными для любого сигнала)
На этом графике мы можем увидеть четыре ярко выраженных максимума, которые соответствуют частотам, присутствующим в сигнале. Самым важным является то, что в отличии от обычного преобразования Фурье мы получаем значения частот относительно оси времени, то есть получаем частотно-временную характеристику сигнала.
Но главной проблемой в использовании оконного преобразования Фурье для получения частотно-временной характеристики сигнала является так называемый принцип неопределенности Гейзенберга, который возникает для параметров времени и частоты сигнала.
В основе принципа неопределенности лежит тот факт, что невозможно сказать точно какая частота присутствует в сигнале в данный момент времени (можно говорить только про диапазон частот) и не возможно сказать в какой точно момент времени частота присутствует в сигнале (можно говорить лишь про период времени).
В связи с этим возникает проблема разрешающей способности. Разрешающую способность оконного преобразования Фурье можно регулировать с помощью ширины окна.
Оконное преобразования Фурье с узким окном в форме Гауссиана с масштабом (обратная величина к ширине окна) 0.01 будет иметь следующий вид:

Как видно, полученное преобразование Фурье имеет хорошую точность относительно времени и плохую точностью относительно частоты (каждый максимум занимает некоторый диапазон частот).
При использовании более широкого окна в форме Гаусианна с масштабом 0.00001 оконное преобразование будет иметь вид:

Видно, что в данном случае мы получаем высокую точность относительно частоты, но при этом очень низкую точность относительно времени.
Можно считать, что обычное преобразование Фурье является оконным преобразованием Фурье с окном шириной в бесконечность.
Таким образом при увеличении ширины окна (уменьшении его разрешающей способности) мы увеличиваем точность относительно частоты и уменьшаем точность относительно времени.
Какое тогда подобрать значение ширины окна, чтобы добиться оптимального соотношения точностей? На этот вопрос отвечает вейвлет-преобразование.
Wavelet-преобразование
Вейвлет преобразование было создано как инструмент, который решает проблему неопределенности Гейзенберга для построение частотно-временных характеристик сигнала.
Вейвлет преобразование сигнала f(t) имеет вид:
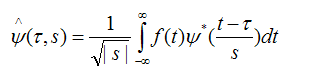
где Tau — сдвиг по времени, S — масштаб, а Psi* — материнский вейвлет.
Понятие вейвлета означает волну, которая проходит через сигнал и является окном некоторой ширины (масштаба) для некоторого местоположения во времени, во время (простите за тавтологию) интегрирования сигнала.
Материнский вейвлет — это функция, которая является прототипом для всех окон, которые будут генерироваться во время вейвлет-преобразования.
Сдвиг по времени регулирует движение генерированных окон по временной компоненте сигнала.
Понятие масштаба является обратным к понятию ширины окна. Чем меньше ширина окна, тем больше масштаб, то есть окно захватывает меньшую часть сигнала и сигнал интегрируется более «детально».
Чем больше ширина окна, тем меньший масштаб, то есть окно захватывает бОльшую часть сигнала и сигнал, соответственно, интегрируется менее «детально».
Опишем процесс вейвлет преобразования (в качестве материнского вейвлета используется гауиссиан) некоторого непрерывного сигнала, который действовал на протяжении некоторого промежутка времени (0-200мс) с нормализованной амплитудой (0-1):
1. Рассчитывается интеграл при начальных условиях Tau=0 и S=1;
а) увеличивается параметр Tau(i) =Tau(i-1)+e на некоторое достаточно малое число e и рассчитывается интеграл. Выполняется пока Tau(i) не станет равным 200мс (концу сигнала).

2. Изменяется параметр S=5, значение Tau опять устанавливается в начальную точку сигнала (Tau=0);
а) увеличивается параметр Tau(i)=Tau(i-1)+e на некоторое достаточно малое число е и рассчитывается интеграл. Выполняется пока Tau(i) не станет равным 200мс (концу сигнала).

Аналогично рассчитываются интегралы для значений параметра S=20, S=50 и т.д.
В результате описанного процесса мы получаем рассчитанные значения интегралов функции для каждого масштаба в каждый момент времени.
Таким образом мы получаем трехмерное представление сигнала с компонентами: масштаб, время и амплитуда (значения рассчитанных интегралов).
Рассмотрим следующий не стационарный сигнал:

Вейвлет преобразования для такого сигнала будет иметь вид:


Таким образом, вейвлет-преобразования, в отличии от оконного преобразования Фурье, которое имеет постоянный масштаб в любой момент времени для всех частот, имеет лучшее представление времени и худшее представление частоты на низких частотах сигнала и лучшее представление частоты с худшим представлением времени на высоких частотах сигнала.
На рисунках хорошо видно, что полученное вейвлет-преобразование является более детализированным по времени в области высоких значений масштаба (низких частот) и менее детализирована в области низких значений масштаба (высоких частот).
Из этого следует, что вейвлет преобразования дает возможность уменьшить влияние принципа неопределенности Гейзенберга на полученном частотно-временном представлении сигнала. С его помощью низкие частоты имеют более детальное представление относительно времени, а высокие — относительно частоты.
Использованная литература: Wavelet-tutorial