Есть хорошая статья Питера Норвига, в которой он рассказывает как написать спеллчекер в 20 строк кода. В этой статье он показывает как поисковые системы могут исправлять ошибки в запросах. И делает это довольно элегантно. Однако, у его подхода есть два серьезных недостатка. Во-первых, исправление более трех ошибок требует больших ресурсов. А гугл, кстати, неплохо справляется и с четырьмя ошибками. Во-вторых, нет возможности проверки связного текста.

Итак, хочется исправить эти проблемы. А именно, написать корректор коротких фраз или запросов, который:
Остальное — под катом.
Для начала решим проблему поиска ошибки в одном слове. Допустим, у нас есть словарь и есть слово для проверки. Мы можем пойти путем, о котором писал Норвиг:
Под генерацией ошибок здесь понимается довольно простая вещь. Для проверяемого слова создается набор слов, которые получаются применением 4-х операций: удаление, вставка, замена и перестановка. К примеру, ошибки замены 'a' на 'о' в слове 'ашибка' дадут следующие слова: ошибка, ааибка, ашабка, ашиака, ашибаа, ашибка. Ясно, что такое проделывается для всех букв алфавита. Подобным образом генерируются варианты слов для вставки, удаления и перестановки.
В этом подходе есть один минус. Если посчитать, то для английского алфавита и слова длиной 5 символов мы получим около 400 вариантов одной ошибки. Для двух ошибок — 160 000. Для трех ошибок — больше шести миллионов. И даже если проверка по словарю происходит за константное время, такое количество вариантов слишком долго генерировать. Да и памяти это отъест прилично.
Мы можем пойти другим путем: сравнить проверяемое слово с каждым словом из словаря, используя какую-нибудь меру сходства. Здесь нам поможет расстояние Левенштейна. Если кратко, расстояние Левенштейна — это минимальное количество операций редактирования, которые нужно применить к первой строке чтобы получить вторую. В классическом варианте рассматриваются три операции: вставка, удаление и замена. К примеру, чтобы из слова «cat» получить «cafe» нам необходимы две операции: одна замена (t->f) и одна вставка (->e).
cat
cafe
Но и здесь есть подвох. Расстояние Левенштейна считается за время O(n*m), где n,m — длины соответствующих строк. Таким образом, посчитать расстояние Левенштейна влоб не представляется возможным. Однако, с этим можно работать, преобразовав словарь в конечный автомат.
Да, да, те самые. А нужны они для того, чтобы представить словарь в виде единой структуры. Эта структура очень похожа на trie, лишь с небольшими отличиями. Итак, конечный автомат — некое логическое устройство, которое получает на вход строку и допускает либо отвергает ее. Можно записать все это формально, но я попробую обойтись без этого, чтобы вид формул никого не усыпил.
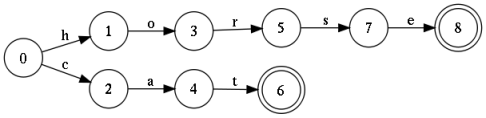
На картинке показан автомат, который принимает на вход любую конечную последовательность символов, но допускает только два слова: 'cat' и 'horse'. Такой автомат называется акцептором. Несложно дополнить эту конструкцию еще несколькими тысячами слов, и в результате получится полноценный словарь. Стоит отметить, что эту конструкцию можно минимизировать, в результате чего она может хранить сотни тысяч слов. Если сохранять условие детерминированности (из любого состояния выходят дуги, не имеющие одинаковых меток), то поиск будет производится за линейное время. И это хорошо.
Но простого акцептора тут недостаточно. Нужно ввести чуть более замысловатую конструкцию, называемую конечным преобразователем (finite state transducer), или трансдьюсером. От акцептора он отличается тем, что каждая дуга имеет два символа: входящий и исходящий. Это позволяет не только «допускать» или «отвергать» строки, но также преобразовывать входящую строку.

Вот пример преобразования строки 'cat' в строку 'fox'.
Преобразователь — это математический объект. Как множество, или, лучше сказать, как регулярное выражение. Как и регулярное выражение, трансдьюсер задает определенный язык, то есть набор строк. Также, трансдьюсеры можно пересекать, объединять, инвертировать и т.п. Но в отличие от регулярного выражения у него есть очень полезная операция, называемая композицией.
Если описать неформально, суть операции заключаются в следующем. Мы проходим одновременно по первому и второму трансдьюсеру, при этом символы на выходе первого «скармливаем» на вход второго. Если нашелся успешный путь как в первом, так и во втором трансдьюсере, мы фиксируем его в новом результирующем трансдьюсере.
Надо сказать, это очень неформальное объяснение. Однако, формализация приведет к необходимости выкатывать целый пласт теории, а это не входило в мои планы. За формальными выкладками можно обратится на википедию. Строгую формализацию дает Мериар Мори (Mehryar Mohri). Он пишет очень интересные статьи на эту тему, хотя и непростые для чтения.
Пора перейти к объяснению, как все же это поможет при вычислении расстояния Левенштейна. Здесь следует отметить, что в трансдьюсере могут участвовать специальные символы, которые обозначают пустую строку (пустой символ, обозначим его 'eps'). Это и позволит нам использовать их как операции редактирования. Все что нам нужно — провести композицию трех трансдьюсеров:
Первые два трансдьюсера представляют входящие строки (см рисунки). Они допускают слова cat и bath.


Модель ошибок представляет собой состояние с рефлексивными (замкнутыми на себя) переходами. Все они, за исключением перехода a:a, представляют операции редактирования:
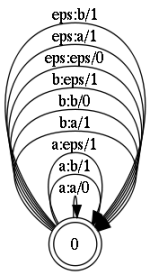
Чтобы не загромождать картинку, на ней показаны коррекции только для двух букв. Тут нужно отметить, что каждый переход маркирован числом. Это обозначения веса коррекции. Т.е. для операций вставки, замены, удаления вес равен 1. Тогда как для перехода типа a:a, который просто транслирует изначальный символ без коррекции, вес равен 0. В результате, итоговая композиция примет следующий вид.
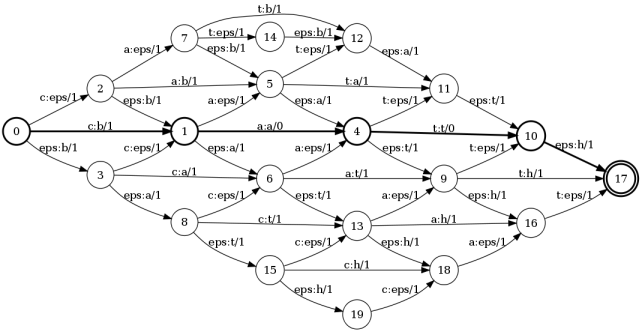
И вот результат: сумма весов вдоль наикратчайшего пути и будет расстоянием Левенштейна. В данном примере таким путем является: 0 — 1 — 4 — 10 — 17. Сумма весов вдоль этого пути равна 2. А теперь проследим за метками вдоль этого пути: c:b a:a t:t eps:h. Это есть ни что иное, как операции редактирования. Т.е. чтобы получить слово bath из слова cat нам необходимо заменить первую букву и добавить 'h' последней.
Итак, мы можем вычислить расстояние Левенштейна между двумя трансдьюсерами. Но это значит, что мы можем вычислить это расстояние между строкой и словарем. Это и позволит вычислить наиболее близкое слово в словаре и даст правильный вариант исправления.
Как исправлять ошибки в отдельных словах уже понятно. Но как исправить ошибку, когда два слова слиплись. Например, если вместо Pen Island кто-то написал penisland. Более того, нужно разделить эти слова правильно, чтобы не травмировать нежную психику пользователя. Кстати, и яндекс и рамблер справляются с задачей хорошо, тогда как mail.ru рубит сплеча.
Чтобы правильно сегментировать или объединять строки необходимо знать, какое словосочетание наиболее вероятно. В статистической лингвистике для этого используются так называемые модели языка, которые строятся обычно на основе ngram'ной модели (или байесовской сети). Здесь я не буду подробно объяснять что это такое. Читатель может глянуть в мой предыдущий пост, где такая модель создается для простого генератора текста.
Хорошая новость заключается в том, что эта модель может быть представлена в виде трансдьсера. Более того, есть готовые библиотеки, которые позволяют рассчитать модель по заданному корпусу. Основная идея заключается в подсчете пар, троек, или n-последовательностей слов, переходу от частот к вероятностям, и построению автомата. Этот автомат делает простую вещь — он оценивает вероятность последовательности слов на входе. Где вероятность больше, ту последовательность и используем.

На рисунке — модель языка для нескольких слов. Картинка кажется несколько запутанной, но алгоритм ее построения несложный. Тем не менее, языковая модель — это тема, требующая отдельной статьи. В ближайшем будущем надеюсь ее написать.
Веса переходов в модели языка — не что иное как вероятность встретить следующее слово. Однако, для числовой стабильности она представлена отрицательным логарифмом. Таким образом веса превращаются в некоторый штраф, и чем штраф меньше, тем наиболее вероятна данная строка.
У нас есть все что нужно для построения спеллчекера. Все что нужно сделать — провести композицию четырех трансдьюсеров:
R = S o E o L o M
и найти кратчайший путь в результирующем трансдьюсере R. Путь, представляющий набор слов и будет искомым вариантом исправления.
Здесь есть пара моментов, требующих пояснения. Во-первых — преобразователь L. Это довольно тривиальный трансдьюсер, «склеивающий» слово из букв для передачи в модель уже целого слова. Таким образом он помогает перейти от букв и символов модели ошибок к словам в модели языка. Второй момент заключается в весах преобразователей. Чтобы произвести корректную композицию необходимо чтобы веса всех преобразователей имели один смысл. Исходная строка и лексикон не имеют весов, модель языка представляет вероятности, но вот модель ошибок дает Левенштейна. Нам необходимо перейти от этой оценки к вероятностям. Этот процесс близок к шаманизму, но тем не менее возможно подобрать такие веса, которые наиболее подходят к реальным ошибкам.
Это, пожалуй и все. Вы можете справедливо спросить, а где же код? А его нет. Все делается с помощью операций над преобразователями. А эти операции уже реализованы в библиотеках. К примеру, в этой: openfst.org. Все что нужно — построить исходные объекты.
Я считаю данный подход очень интересным. Он обладает рядом сильных сторон. Первой сильной стороной является то, что мы не пишем код, а просто оперируем математическими объектами. Это упрощает разработку инструментов работы с текстом и очень сильно экономит время.
Другой сильной стороной является его универсальность. Не нужно писать различные алгоритмы для операций со строками. К примеру, если понадобиться определять ошибки неверной раскладки вида «fkujhbnv» -> «алгоритм», то для этого не нужно писать новую программу. Достаточно немного модифицировать модель ошибок: добавить переходы, маркированные буквами двух языков и пару состояний.
Однако, есть и отрицательные стороны. Довольно не тривиально добиться стабильной и быстрой скорости. У меня не получилось. Скорость работы сильно зависит от структуры преобразователей, количества переходов, меры недетерминированности. Кроме того, некоторые операции над преобразователями требуют больших объемов памяти. Но все эти вопросы так или иначе разрешимы.
Надеюсь, статья была полезной. Задавайте вопросы, если что-то непонятно. Охотно отвечу.

Итак, хочется исправить эти проблемы. А именно, написать корректор коротких фраз или запросов, который:
- умел бы выявлять три (и более) ошибки в запросе;
- умел бы проверять «разорванные» или «слипшиеся» фразы, например expertsexchange — experts_exchange, ma na ger — manager
- не требовал много кода для реализации
- мог бы достраиваться до исправления ошибок на других языках и других типов" ошибок
Остальное — под катом.
Как определять ошибку
Для начала решим проблему поиска ошибки в одном слове. Допустим, у нас есть словарь и есть слово для проверки. Мы можем пойти путем, о котором писал Норвиг:
- поверить слово в словаре
- если нет, сгенерировать однобуквенные ошибки, и проверить в словаре
- если опять неудача, сгенерирвоать двубуквенные ошибки, и снова по словарю
Под генерацией ошибок здесь понимается довольно простая вещь. Для проверяемого слова создается набор слов, которые получаются применением 4-х операций: удаление, вставка, замена и перестановка. К примеру, ошибки замены 'a' на 'о' в слове 'ашибка' дадут следующие слова: ошибка, ааибка, ашабка, ашиака, ашибаа, ашибка. Ясно, что такое проделывается для всех букв алфавита. Подобным образом генерируются варианты слов для вставки, удаления и перестановки.
В этом подходе есть один минус. Если посчитать, то для английского алфавита и слова длиной 5 символов мы получим около 400 вариантов одной ошибки. Для двух ошибок — 160 000. Для трех ошибок — больше шести миллионов. И даже если проверка по словарю происходит за константное время, такое количество вариантов слишком долго генерировать. Да и памяти это отъест прилично.
Мы можем пойти другим путем: сравнить проверяемое слово с каждым словом из словаря, используя какую-нибудь меру сходства. Здесь нам поможет расстояние Левенштейна. Если кратко, расстояние Левенштейна — это минимальное количество операций редактирования, которые нужно применить к первой строке чтобы получить вторую. В классическом варианте рассматриваются три операции: вставка, удаление и замена. К примеру, чтобы из слова «cat» получить «cafe» нам необходимы две операции: одна замена (t->f) и одна вставка (->e).
cat
cafe
Но и здесь есть подвох. Расстояние Левенштейна считается за время O(n*m), где n,m — длины соответствующих строк. Таким образом, посчитать расстояние Левенштейна влоб не представляется возможным. Однако, с этим можно работать, преобразовав словарь в конечный автомат.
Конечные автоматы
Да, да, те самые. А нужны они для того, чтобы представить словарь в виде единой структуры. Эта структура очень похожа на trie, лишь с небольшими отличиями. Итак, конечный автомат — некое логическое устройство, которое получает на вход строку и допускает либо отвергает ее. Можно записать все это формально, но я попробую обойтись без этого, чтобы вид формул никого не усыпил.

На картинке показан автомат, который принимает на вход любую конечную последовательность символов, но допускает только два слова: 'cat' и 'horse'. Такой автомат называется акцептором. Несложно дополнить эту конструкцию еще несколькими тысячами слов, и в результате получится полноценный словарь. Стоит отметить, что эту конструкцию можно минимизировать, в результате чего она может хранить сотни тысяч слов. Если сохранять условие детерминированности (из любого состояния выходят дуги, не имеющие одинаковых меток), то поиск будет производится за линейное время. И это хорошо.
Но простого акцептора тут недостаточно. Нужно ввести чуть более замысловатую конструкцию, называемую конечным преобразователем (finite state transducer), или трансдьюсером. От акцептора он отличается тем, что каждая дуга имеет два символа: входящий и исходящий. Это позволяет не только «допускать» или «отвергать» строки, но также преобразовывать входящую строку.

Вот пример преобразования строки 'cat' в строку 'fox'.
Композиция автоматов
Преобразователь — это математический объект. Как множество, или, лучше сказать, как регулярное выражение. Как и регулярное выражение, трансдьюсер задает определенный язык, то есть набор строк. Также, трансдьюсеры можно пересекать, объединять, инвертировать и т.п. Но в отличие от регулярного выражения у него есть очень полезная операция, называемая композицией.
Если описать неформально, суть операции заключаются в следующем. Мы проходим одновременно по первому и второму трансдьюсеру, при этом символы на выходе первого «скармливаем» на вход второго. Если нашелся успешный путь как в первом, так и во втором трансдьюсере, мы фиксируем его в новом результирующем трансдьюсере.
Надо сказать, это очень неформальное объяснение. Однако, формализация приведет к необходимости выкатывать целый пласт теории, а это не входило в мои планы. За формальными выкладками можно обратится на википедию. Строгую формализацию дает Мериар Мори (Mehryar Mohri). Он пишет очень интересные статьи на эту тему, хотя и непростые для чтения.
Расстояние Левенштейна через композицию
Пора перейти к объяснению, как все же это поможет при вычислении расстояния Левенштейна. Здесь следует отметить, что в трансдьюсере могут участвовать специальные символы, которые обозначают пустую строку (пустой символ, обозначим его 'eps'). Это и позволит нам использовать их как операции редактирования. Все что нам нужно — провести композицию трех трансдьюсеров:
- трансдьюсер, представляющий первое слово
- трансдьюсер, представляющий модель ошибок
- трансдьюсер, представляющий второе слово
Первые два трансдьюсера представляют входящие строки (см рисунки). Они допускают слова cat и bath.


Модель ошибок представляет собой состояние с рефлексивными (замкнутыми на себя) переходами. Все они, за исключением перехода a:a, представляют операции редактирования:
- a:a — оставляем символ без изменения
- a:b — замена символа; здесь 'a' на 'b'
- eps:a — вставка символа
- a:eps — удаление символа символа

Чтобы не загромождать картинку, на ней показаны коррекции только для двух букв. Тут нужно отметить, что каждый переход маркирован числом. Это обозначения веса коррекции. Т.е. для операций вставки, замены, удаления вес равен 1. Тогда как для перехода типа a:a, который просто транслирует изначальный символ без коррекции, вес равен 0. В результате, итоговая композиция примет следующий вид.

И вот результат: сумма весов вдоль наикратчайшего пути и будет расстоянием Левенштейна. В данном примере таким путем является: 0 — 1 — 4 — 10 — 17. Сумма весов вдоль этого пути равна 2. А теперь проследим за метками вдоль этого пути: c:b a:a t:t eps:h. Это есть ни что иное, как операции редактирования. Т.е. чтобы получить слово bath из слова cat нам необходимо заменить первую букву и добавить 'h' последней.
Итак, мы можем вычислить расстояние Левенштейна между двумя трансдьюсерами. Но это значит, что мы можем вычислить это расстояние между строкой и словарем. Это и позволит вычислить наиболее близкое слово в словаре и даст правильный вариант исправления.
Языковая модель
Как исправлять ошибки в отдельных словах уже понятно. Но как исправить ошибку, когда два слова слиплись. Например, если вместо Pen Island кто-то написал penisland. Более того, нужно разделить эти слова правильно, чтобы не травмировать нежную психику пользователя. Кстати, и яндекс и рамблер справляются с задачей хорошо, тогда как mail.ru рубит сплеча.
Чтобы правильно сегментировать или объединять строки необходимо знать, какое словосочетание наиболее вероятно. В статистической лингвистике для этого используются так называемые модели языка, которые строятся обычно на основе ngram'ной модели (или байесовской сети). Здесь я не буду подробно объяснять что это такое. Читатель может глянуть в мой предыдущий пост, где такая модель создается для простого генератора текста.
Хорошая новость заключается в том, что эта модель может быть представлена в виде трансдьсера. Более того, есть готовые библиотеки, которые позволяют рассчитать модель по заданному корпусу. Основная идея заключается в подсчете пар, троек, или n-последовательностей слов, переходу от частот к вероятностям, и построению автомата. Этот автомат делает простую вещь — он оценивает вероятность последовательности слов на входе. Где вероятность больше, ту последовательность и используем.

На рисунке — модель языка для нескольких слов. Картинка кажется несколько запутанной, но алгоритм ее построения несложный. Тем не менее, языковая модель — это тема, требующая отдельной статьи. В ближайшем будущем надеюсь ее написать.
Веса переходов в модели языка — не что иное как вероятность встретить следующее слово. Однако, для числовой стабильности она представлена отрицательным логарифмом. Таким образом веса превращаются в некоторый штраф, и чем штраф меньше, тем наиболее вероятна данная строка.
Собираем все вместе
У нас есть все что нужно для построения спеллчекера. Все что нужно сделать — провести композицию четырех трансдьюсеров:
R = S o E o L o M
- S — исходная строка
- E — модель ошибок
- L — лексикон
- M — модель языка
и найти кратчайший путь в результирующем трансдьюсере R. Путь, представляющий набор слов и будет искомым вариантом исправления.
Здесь есть пара моментов, требующих пояснения. Во-первых — преобразователь L. Это довольно тривиальный трансдьюсер, «склеивающий» слово из букв для передачи в модель уже целого слова. Таким образом он помогает перейти от букв и символов модели ошибок к словам в модели языка. Второй момент заключается в весах преобразователей. Чтобы произвести корректную композицию необходимо чтобы веса всех преобразователей имели один смысл. Исходная строка и лексикон не имеют весов, модель языка представляет вероятности, но вот модель ошибок дает Левенштейна. Нам необходимо перейти от этой оценки к вероятностям. Этот процесс близок к шаманизму, но тем не менее возможно подобрать такие веса, которые наиболее подходят к реальным ошибкам.
Это, пожалуй и все. Вы можете справедливо спросить, а где же код? А его нет. Все делается с помощью операций над преобразователями. А эти операции уже реализованы в библиотеках. К примеру, в этой: openfst.org. Все что нужно — построить исходные объекты.
Выводы, pro et contra
Я считаю данный подход очень интересным. Он обладает рядом сильных сторон. Первой сильной стороной является то, что мы не пишем код, а просто оперируем математическими объектами. Это упрощает разработку инструментов работы с текстом и очень сильно экономит время.
Другой сильной стороной является его универсальность. Не нужно писать различные алгоритмы для операций со строками. К примеру, если понадобиться определять ошибки неверной раскладки вида «fkujhbnv» -> «алгоритм», то для этого не нужно писать новую программу. Достаточно немного модифицировать модель ошибок: добавить переходы, маркированные буквами двух языков и пару состояний.
Однако, есть и отрицательные стороны. Довольно не тривиально добиться стабильной и быстрой скорости. У меня не получилось. Скорость работы сильно зависит от структуры преобразователей, количества переходов, меры недетерминированности. Кроме того, некоторые операции над преобразователями требуют больших объемов памяти. Но все эти вопросы так или иначе разрешимы.
Надеюсь, статья была полезной. Задавайте вопросы, если что-то непонятно. Охотно отвечу.