UPD. 2025. The demo of Graph Unfolding Cellular Automata (GUCA) has been re-implemented in TypeScript: https://github.com/roma-goodok/guca
Пожалуй, ничто так долго, на протяжении многих веков, не интересовало учёных, как вопросы о происхождении жизни и разума. Как природа догадалась сотворить человеческий мозг? Чем определяется структура нейронной сети в нашей голове и как работает автосборка многоклеточного организма из единственной клетки? Почему при развитии зародыша человека на определённой стадии можно наблюдать нечто похожее на рыбьи жабры?
Да и простого любопытствующего обывателя, не отягощённого подробностями органической химии, подобные вопросы не обходят стороной.
Вот была бы игрушка-конструктор, с помощью которой можно собрать простенькие растущие организмы. Тогда построив предельно упрощённую модель, демонстрирующую многие из явлений живого, можно было бы приблизиться к ответам на вопросы устройства жизни, или хотя бы к пониманию, где эти ответы искать.
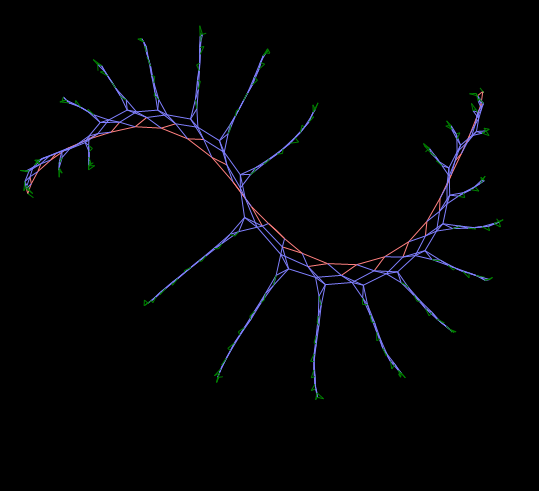
Такой предельно упрощённой и наглядной моделью могут оказаться «Живые графы» — конечные автоматы на графе, каждый узел которого содержит некое исполняющее устройство (автомат) с конечным числом состояний и с набором примитивных правил, управляющих созданием или изменением новых связей между узлами.
В статье будет рассказано об одном из воплощений «Живого графа» — о клеточном автомате развёртывания графа GUCA (Graph Unfolding Cellular Automata). Демонстрацию работы GUСА можно «пощупать» прямо в браузере с подключённым Silverlight-плагином. Веб-приложение визуализирует короткую жизнь некоторых моих первых экземпляров растущих графов – как собственноручно сконструированных продуктов «генной инженерии», так и «естественно-отобранных» генетическим алгоритмом форм.
Даже если начальный граф будет состоять только из одного узла, а все порождающиеся узлы графа будут иметь одну и ту же копию набора правил с каждой новой итерации срабатывания правил можно будет наблюдать развитие самых разнообразных структур. Легко заметить, что начальный узел — аналогичен зародышу многоклеточного организма, остальные узлы графа аналогичны клеткам, наборы правил – хромосоме, а сами правила – генам.
А всё началось с увлечения искусственными нейронными сетями (ИНС), при исследовании которых и родилась идея GUCA.
Небольшое напоминание. Искусственные нейронные сети, нашедшие широкое применения в искусственных же системах управления, можно представить как соединённые между собой «нейроны», сами по себе выполняющие достаточно простые операции, например, суммирование входящих сигналов и преобразование получившегося значения. Но будучи соединёнными по некоторым правилам в единую сеть «нейроны» образуют систему, возможности которой заметно превышают возможности cоставляющих её элементов — того же сумматора. Системе в целом уже доступны функции распознавания образов, классификации, фильтрации сигналов – всё то, что необходимо для построения сложной «интеллектуальной» системы управления.
На заре использования нейронных сетей топология сети задавалась исследователем, а параметры связей подбирались по наперёд заданному алгоритму, использующему накопленные данные о решаемой задаче. Если для достаточно простых типов нейронов задача построения топологии сети была достаточно детерминированной и решаемой (что не означает при этом решаемости самой задачи предметной области), то при использовании каскадов нейронных нелинейных динамических сетей с обратными связями, задача эта оказывалась не тривиальной и возникла идея поручить построение топологии нейронной сети компьютеру. На помощь пришли методы, подсмотренные в самой природе.
Речь идёт об нейроэволюционных методах,, в которых для построения топологий нейронных сетей используются генетические алгоритмы.
Обзор таких методов был недавно опубликован на хабре: [1] habrahabr.ru/blogs/artificial_intelligence/84015,
Я не буду пересказывать уже известные способы реализации таких алгоритмов, напомню лишь основные положения косвенного кодирования сетей/графов, также лежащие в основе рассматриваемого метода GUCA, реализацию которого отличает лишь локальность, контекстный выбор применяемых правил и «запрограммированная смерть».
В косвенных методах кодирования нейронных сетей, в «геноме» экземпляра сети топология задаётся не явным перечислением узлов и связей, а косвенно через правила построения сети из небольшого её фрагмента. Ведь именно таким способом развивается организм животного из маленького зародыша, да и человеческий мозг.
Напомню также, что генетический алгоритм обеспечивает: случайную генерацию или модификацию кодов, оценку «результата» декодирования «генома» (т.е. оценку получившейся нейронной сети с помощью фитнесс-функции) и отбор лучших представителей.
Для нейронных систем выполняющих роль систем управления объектами (роботами, манипуляторами), фитнесс-функцией может стать работоспособность объекта управления в некой среде (лабиринте, при обращение с предметами, в полёте, в бою и т.п)
При этом косвенные способы кодирования обеспечивают следующие свойства:
1) Модульность. Рекурсивное построение фрактальных структур по простым правилам и повторение в конструкции организма неких стандартных блоков, элементов.
2) Полнота. Для любого заданной сети (графа) можно подобрать код.
3) Избыточность. Код может содержать избыточные данные никак не влияющие на результат декодирования
4) (При условии использования в правилах кодирования контекста)
a. Порождение топологии в зависимости от проходящих в нейронной сети сигналов
b. Регенерация — восстанавливаемость при локальных повреждениях
Из обзора [1] видно, что основные усилия исследователей направлены на изобретение более-менее удачных способов кодирования именно топологии сети, нежели на конструирование принципов работы нейрона/сети и кодирование её параметров, что не удивительно – ведь именно топология и определяет работу всей системы «нейронная сеть».
Действительно, было бы полезно выделить в отдельную задачу проблему «выращивание» топологии сети с применением всё того же генетического алгоритма и косвенного кодирования (по сути – направленного графа, а ещё более абстрагируясь от НС – ненаправленного графа). Фитнесс-функцией (определяющей успешность выживания экземпляра) будет уже не способность нейронной сети справится с управляемым объектов, а, например, геометрические свойства топологии. Если же развернуть граф на плоскости или в пространстве — то оценкой приспособленности графа могут быть свойства получившегося изображения, в т.ч. растрового.
Концентрация усилий на более узкой задаче (построение топологий, абстрагируясь от нейронной сети) позволит:
• Найти более широкое применение в областях отличных от ИНС (автосборка механизмов, конфигурация распределённых вычислений в компьютерной сети или вирусов, взаимодействие боевых роботов).
• Наглядно представить результат (не только конечный, но и промежуточный) для исследователя, что может помочь при отработке алгоритмов лучше понимать причинно-следственные связи. К тому же, наглядное представление может подсказать идеи/решения/тупики.
• Объективней сравнивать различные решения по кодированию топологии или комбинировать удачные решения по кодированию топологии с различными конструкциями «нейронов». Объективно – т.е. независимо от конкретной предметной области применения.
• Проще (быстрее и дешевле) рассчитывать фитнес-функции (по сравнению с оценкой пригодности нейронной сети в качестве системы управления) – т.е. исследовать именно топологические алгоритмы, не затрачивая дополнительные ресурсы, в том числе и вычислительные, на производные задачи.
При этом, такие любопытные свойства как вышеперечисленные «модульность», «регенерация» — останутся доступными для исследования.
Можно добавить, что эволюция мозга животных также берёт начало от результата, достигнутого эволюцией формы многоклеточного организма (осе симметричность — хрящ – позвоночник — спинной мозг – несимметричность — головное уплотнение мозга).
Одним из таких методов и является клеточный автомат развёртывания графа GUCA, принципы работы которого будут изложены в следующем разделе.
«Живой граф» GUCA – это конечный клеточный автомат, в котором каждый узел находится в одном из состояний (количество состояний конечно), и может переходить в другое состояние по определённым правилам, зависящим как от состояния самого узла, так и от его окружения. Эти правила едины для всех узлов, неизменны во времени и отрабатываются синхронно для всех узлов одновременно.
Классический представитель клеточного автомата – игра «Жизнь». Основное отличие «Живых графов» от классической игры «Жизнь» и её вариаций заключается в том что «внутриклеточные» автоматы расположены не на прямоугольной плоскости, а находятся в узлах графа с переменным количеством связанных соседей.
При этом, в отличии от большинства методов кодирования топологии сети описанных в обзоре [1], «Живой граф» GUCA исповедует следующие принципы:
• Контекстный выбор применяемых правил
• Только локальные и одношаговые изменения
• Не только рождение, но и смерть
Как ни странно, все эти особенности изначально присущи и клеточному автомату «Жизнь», хотя и были выбраны в результате долгих поисков наборов правил и операций, решающих задачу
развёртывания графа наиболее просто и полно.
Впрочем, операция удаления предлагалась в одном из упражнении курса лекций [2]
Итак, в «Живом графе» GUCA узел находится в одном из состояний. И есть правила, по которым при определённых условиях срабатывания производятся операции над графом.
Примером набора правил, которые удовлетворяют вышеописанным «метаправилам» для некоторого экземпляра «живого графа» может служить такой список:
1. «Если узел находится в состоянии А, то создать связанный узел в состоянии В»
2. «Если узел находиться в состоянии В, и количество связей меньше двух, то создать связанный узел в состоянии В»
3. «Если узел находится в состоянии В и предыдущее состояние было B, то перейти в состояние С»
4.…
Состояние – один из элементов конечного множества. Можно обозначать числом или буквой алфавита – А, B, С, D,….
Операции. Понятно, что над графами можно проводить самые разные операции – добавлять/разделять узлы, замещать узлы связанной группой, объединять узлы. Я остановился на четырёх примитивных операциях, которых, похоже, будет вполне достаточно для воспроизведения любой сколь угодно сложной структуры.
• Переход узла в состояние X (таким образом, состояние X – это операнд операции)
• Рождение нового узла, связанного с текущим. Состояние нового узла X
• Соединение узла с ближайшим не соединённым узлом, находящимся в состоянии X
• Отсоединение узла, находящегося в состоянии X
Теперь об условиях, диктующих совершение операции в правиле. Я не ограничился зависимости от текущего состояния узла и количеством связей между этим узлом и другими узлами. К этим условиям добавил зависимости от предыдущего состояния узла и зависимость от числа родителей/делений узла (ведь каждый узел, согласно списку операций, порождён одним и только одним узлом-родителем).
Условия:
• Узел находится в состоянии X
• Предыдущее состояние узла равно Y
• Количество связей узла – от С1 до С2
• Количество предков узла (от которых он родился) – от P1 до P2.
Последнее условие и счётчик количества делений узла (аналог теломеразы) введены, чтобы обеспечить остановку развития всего организма и/или отдельных его модулей.
Я также рассматривал операции «соединение узла со всеми узлами в состоянии X», «смерть узла» — но посчитал их избыточными. Подумываю также ввести операцию «сброс счётчика делений». Отмечу, что все операции локальны и «вертятся» вокруг узла (изменяют только узел или его ближайшее окружение).
Впрочем, возможно, читатель сможет найти более стройную систему правил.
Правила GUCA можно записать и в краткой форме, обозначив текущее состояние – буквой, предыдущее – буквой в скобках, количество соседей – символом «с» (от connections), количество родителей – «p» (от parents). Если предыдущее состояние игнорируется в условии, то в скобкам будем указывать прочерк. Разделим в записи правила операции от условий символом двоеточия, а возможные операции обозначим следующим образом:
• Операцию перехода в другое состояние X обозначим X
• Операцию рождения связанного узла Ч обозначим ++X
• Операцию соединения с узлом X обозначим +X
• Операцию отсоединения от узла X обозначим –X
Тогда, для некоторого экземпляра «живого графа» набор правил будет записан с помощью грамматики:
1. А(А),p=0 :++B
2. B(-), c <2 :++B
3. B(B) :C
4. A(A) :G
5. C(B), c=1 :G
6. G(G), c <5 :H
Если начальный узел графа будет в состоянии «А», то через 12 последовательных итераций применения правил, мы получим «Пальцастую гантельку»:
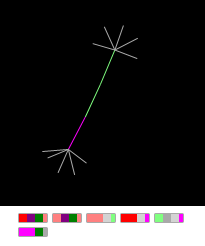
Рисунок Граф «Пальцастая гантелька» и условное отображение её карты генов.
Это самый первый граф, сконструированный мною несколько лет назад для отладки конечного автомата на графах. Он настолько прост и понятен, что упоминаю его лишь для того, чтобы отдать дань уважения первопроходцу. Правила заложенные в его «геноме» просты: из узла с начальным состоянием А рождается короткая ниточка, оканчивающаяся узлами (в состоянии G), для которых срабатывает правило: пока количество соседей меньше или равно пяти — создать нового соседа.
Здесь и далее, при отображении графа на плоскости и на условном отображении карты генов красным цветом обозначается состояние А, розовым – B, зелёным – С, малиновым — G.
Выключив ген №5 из «пальцастой гантельки» можно сотворить «уродца» — «рука обыкновенная»:
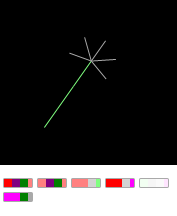
Если включить ген обратно, вторая «рука» вырастит обратно.
Таким образом, набор простых правил может определять топологию графа. Вообще говоря, топологию графа определяет не только набор правил и начальное состояние его узла(узлов), но и некоторые глобальные ограничения – например максимальное количество итерации или максимально возможное количество соединений узлов.
Одним из способов убедиться, что описанная выше система правил достаточна для построения графов любой топологии — является решение «контрольных задачек» на построение. Задумав ту или иную фигуру постараться придумать «ген», из которого она и родится. И если задуманную фигуру не удастся никаким образом сконструировать, то система правил вряд ли будет пригодна не только для выращивание графов, но и для построения сложной искусственной нейронной сети.
«Контрольные задачи» должны быть с одной стороны предельно простыми, с другой стороны «показательными» (прошу не путать со «зрелищными») для демонстрации качественных свойств и эффектов сложного живого организма — модульности, гибридизации, самовосстанавливаемости… причудливости, наконец. Такими примерами могут быть – простейшие фракталы, растущие изнутри фигуры, сетки с большим количеством ячеек и просто «дикорастущие» растения.
Некоторые из этих задач было крайне сложно (долго) и не надёжно (ответ часто не сходился) решать в уме или на бумаге, и чтобы провести эти первые эксперименты, пришлось вооружить себя «экспериментальной установкой».
Такой экспериментальной установкой стало программное приложение, позволяющее отладить «генетический код» и машину воспроизведения. Кроме этого, с её помощью можно:
• наглядно представить процесс роста графа,
• наглядно отобразить цветную «карту» хромосомы и активность генов в процессе роста графа
• посмотреть к чему приведёт выключение того или иной гена или разрезание «живого графа».
Демонстрационная Silverlight версия «экспериментальной установки» доступна по адресу http://roma.goodok.ru/guca/GUCA_DemoSL.html

Рисунок Silverlight версия «Экспериментальной установка» по выращиванию графа позволяет наблюдать процесс развития графа, активность генов на карте хромосомы, «подрезать» ножом отдельные веточки.
Чтобы запустить разворачивания графа, нужно на правой «панели управления» выбрать из выпадающего списка пример (Select sample) и нажать на кнопку запуска («Start»).
В центральной области с чёрным фоном будет отображаться граф в процессе его роста из единственного узла-зародыша. Различные состояния узлов отображаются соответствующим цветом. Можно изменить масштаб и вид отображения или замедлить рост графа, чтобы рассмотреть детали процесса.
Можно не только наблюдать развитие и жизнь графа, но и вмешиваться в этот процесс, надрезая «скальпелем» (переключатель «Knife») или выключая тот или иной ген, выводя на свет «уродцев», добиваясь «летального исхода» или «раковой опухли»
Справа внизу условно отображается «карта» хромосомы («Genome») — каждый прямоугольник на ней соответствует «гену» (пункту правила). Опять же таки, цветом кодируются состояния узлов в условии правила, само правило и состояние узла в операнде правила. В процессе роста графа зелёной подсветкой отмечаются те гены, которые были активны во время очередной итерации исполнения правил.
Наведя мышкой на прямоугольник отдельного «гена», можно увидеть расшифровку кодируемого геном правила в виде текста, а нажав кнопку мыши, выключить (или включить обратно) выбранный ген.
В этой статье я не буду останавливаться на описании устройства «лабораторной установки», хотя сама по себе её «сборка» была весьма интересным занятием – кроме теории графов и дискретной математики, пригодились знания и опыт численного решения уравнений математической физики, геометрии и пр. К тому же сам её генетический «исходный» код сам по себе является результатом эволюции и содержит в себе наследие далёких предков – ведь первая версия и проектные решения были реализованы на Delphi 7.0. Можно даже сказать, это мой первый «Hellow World!» на платформе Silverlight|WPF. Отмечу лишь, использование библиотек QuickGraph (графы и алгоритмы) и AForge (генетический алгоритм).
Итак, давайте посмотрим некоторые простейшие примеры «живых графов», демонстрирующие живые свойства. Некоторые из экземпляров (например, вышеупомянутая «пальцастая гантелька») были сконструированы только божественным для мира живых графов началом (т.е. Мной), другие — результат эволюции, а третьи являются генетически модифицированными продуктами.
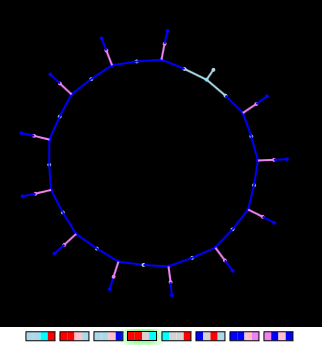
Это фигура – генетически модифицированный продукт! Сначала с помощью генетического алгоритма была получена бесконечно растущая изнутри окружность (фитнесс-функция при этом зависела только от топологических характеристик графа – обязательного наличия двух граней). Затем, был добавлен ещё один «ген» — «ген волос» (крайний справа на карте генов)
Запуская растущий изнутри «организм» можно наблюдать, как отдельные сегменты окружности появляются в результате циклического повторения операций вставки новых рёбер.
Если взять гены «пальцастой гантельки» и «волосатой окружности» и объединить их в одной хромосоме «зародыша», то из него вырастет гибрид, унаследовавший как свойства «пальцастости» гантельки, так и «округлые» свойства:
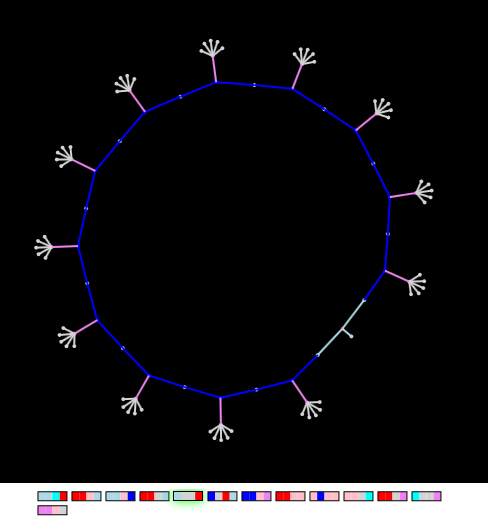
Рисунок Гибрид «пальцастой гантельки» и «волосатой окружности» имеет общие свойства
Обратите внимание, что часть генов «пальцастой гантельки» во время всего процесса развёртывания графа остаются неактивными (на карте генов активность генов отмечается зелёной подсветкой).
Простейший генетический код из двух «генов» создаёт сколь угодно большой по размерам граф». Если отрезать любую его ветку, то «куст» почти мгновенно восстановиться в прежних размерах и формах.
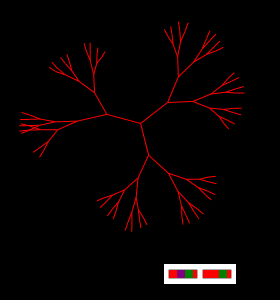
Рисунок Примитивный фрактал задаётся лишь парой генов
Эта и следующие две странные фигуры – результат моих попыток сконструировать квадратную сетку в виде квадрата.
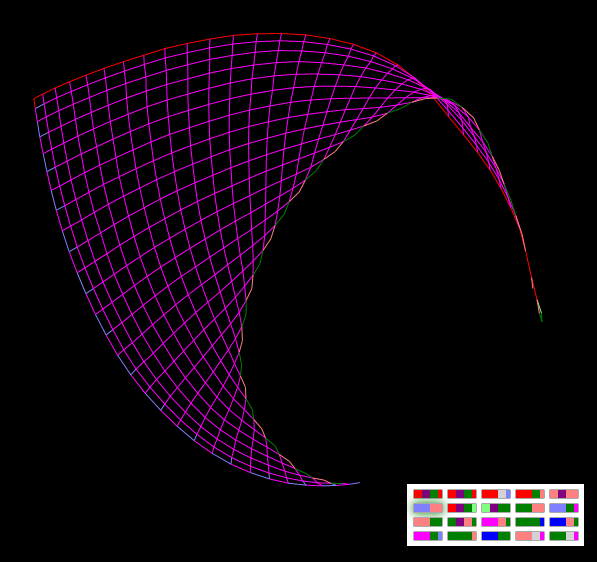
Рисунок «Кокошник» — разворачивание прямоугольной сетки
Изменяя пару генов, можно выращивать сколь угодно большую (и малую) сетку. Ножом можно делать дырки. Попробуйте выключить ген №13 «O(O):+L» и включить его после разворачивания.
«Странная фигура 1» — это моя ошибка. На самом деле целью было создание равносторонней квадратной сетки. Фигура изображена на самом первом в статье рисунке (Рисунок 1). Если же подрезать её отростки прямо на живом графе, то, выпустив взамен отрезанных новые отростки, фигура примет более размашистый вид:
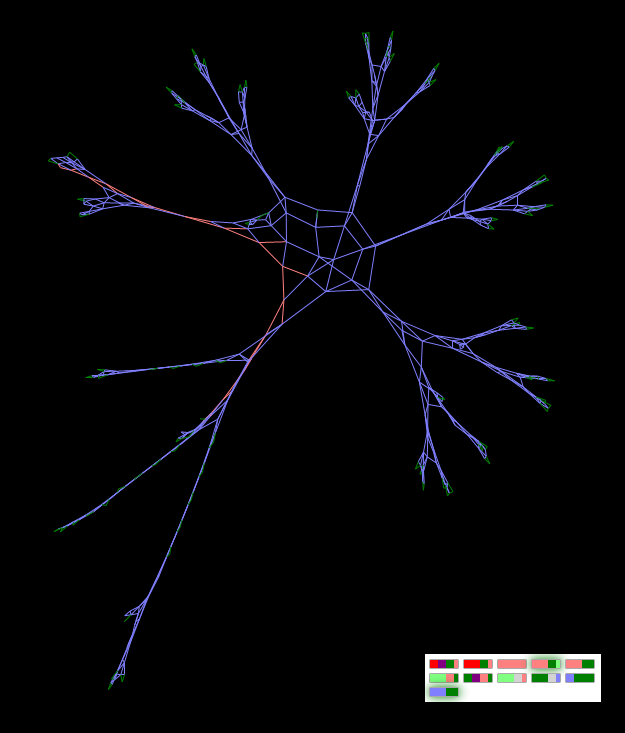
Рисунок «Странная фигура» после обрезания
Странная фигура 2. Хромосома этой фигуры отличается от хромосомы «Странной фигуры 2» всего лишь одним геном, точнее даже частью гена (близкие родственники), а вот форма результата «декодирования» мало похоже на форму предыдущего экземпляра.
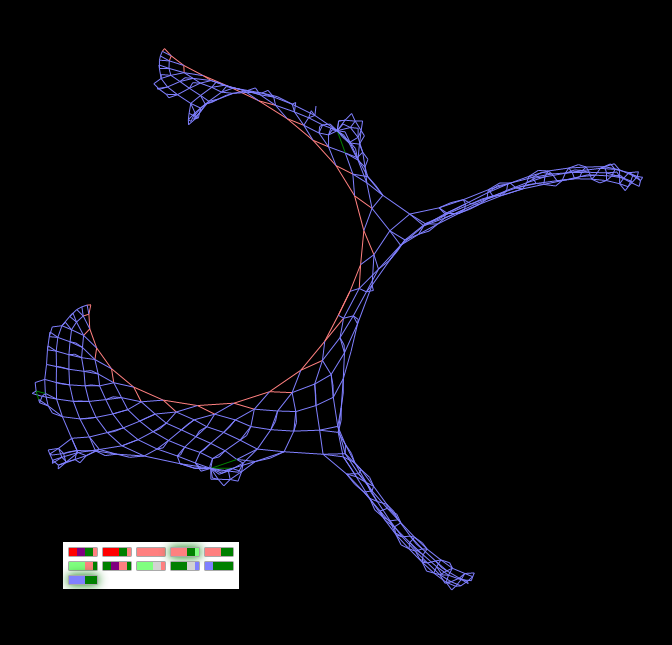
«Странная фигура 2» – близкий родственник «Странной фигуры 1» — отличается всего лишь одним геном
Чтобы получить 10 генов этой фигуры потребовались тысячи итераций генетического алгоритма. Фитнесс функция в переводе на русский звучала примерно так: «чем ближе количество граней к двум, и число узлов степени 1 к шести и число узлов степени 3 к шести и число генов к нулю – тем больше шансов выжить у графа»(степень узла – количество связей)
Эволюция этого вида пережила несколько скачков: треугольник, квадрат с отростками, шести угольник с неправильными отростками, и, наконец, правильный. Замедлив процесс разворачивания, можно увидеть, какое решение нашла эволюция для построения фигуры.
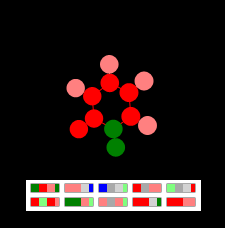
Рисунок Шестиугольник с «листьями» — Результат работы генетического алгоритма
Итак, мы увидели как с помощью таких абстрактных объектов как конечные автоматы и графы, можно создавать системы, забавным образом похожие на многоклеточные живые организмы, что демонстрирует общность принципов лежащих в основе «живых графов» и в законах образования геометрических форм живого.
Однако это не означает, что мы раскрыли тайны жизни. Это просто означает, что можно двигаться дальше: исследовать закономерности эволюций «живых графов». Напомню, что в демонстрационном приложении мы наблюдали «онтогенез» и результат эволюции, а не саму эволюцию.
Вопросами последующих исследований могут быть как определение границ модели «живых графов», так и поиск количественных и качественных закономерностей в неотягощённой излишними подробностями эволюционной модели (зависимость длин гена от сложности форм, статистики генетической информации от положения вида в дереве эволюции, скорости эволюции от набора допустимых операций и т.п.).
По результатам этих исследований, определив наиболее эффективные эволюционные алгоритмы, можно попробовать применить «живые графы» в исходной области: в искусственных нейронных сетях или в исследовании эволюции роботов, «аниматов», искусственных систем управления. Особый интерес представляет комбинация динамических нелинейных нейронных сетей с живыми графами, в которой состояние возбуждённости нейрона является одним из состояний конечного автомата «внутри» живого графа. Можно будет наблюдать что-то вроде «генетической памяти».
Также, было бы любопытно создать материальное воплощение живых графов в виде самоорганизующейся колонии примитивных роботов, в прошивку которых зашит генетический код сообщества.
Все эти направления трудно охватить исследователю-одиночке, и я надеюсь, некоторые из читателей ещё совершат свои маленькие и большие открытия в этой области исследований. Вполне возможно, модели подобные «Живым графам» станут отправной точкой для ваших собственных исследований. Правда, для этого понадобятся уже другие «экспериментальные установки».
[1] «Обзор методов эволюции нейронных сетей» http://habrahabr.ru/blogs/artificial_intelligence/84015/
[2] «Evolutionary Computation for Modeling and Optimization» Daniel Ashlock, January 12, 2004 http://orion.math.iastate.edu/danwell/ma378/
UPDATE Добавил возможность загрузить «геном» из xml. Пример файла: геном «странной фигуры 1». Теперь вы можете попробовать вырастить свои графы, проверить свои задумки… найти ошибки, наконец.
UPDATE 2 Выложил исходники (1.8Мб) с релизной сборкой.
Введение
Пожалуй, ничто так долго, на протяжении многих веков, не интересовало учёных, как вопросы о происхождении жизни и разума. Как природа догадалась сотворить человеческий мозг? Чем определяется структура нейронной сети в нашей голове и как работает автосборка многоклеточного организма из единственной клетки? Почему при развитии зародыша человека на определённой стадии можно наблюдать нечто похожее на рыбьи жабры?
Да и простого любопытствующего обывателя, не отягощённого подробностями органической химии, подобные вопросы не обходят стороной.
Вот была бы игрушка-конструктор, с помощью которой можно собрать простенькие растущие организмы. Тогда построив предельно упрощённую модель, демонстрирующую многие из явлений живого, можно было бы приблизиться к ответам на вопросы устройства жизни, или хотя бы к пониманию, где эти ответы искать.

Такой предельно упрощённой и наглядной моделью могут оказаться «Живые графы» — конечные автоматы на графе, каждый узел которого содержит некое исполняющее устройство (автомат) с конечным числом состояний и с набором примитивных правил, управляющих созданием или изменением новых связей между узлами.
«Вы только посмотрите, какую я вырастил капусту!» (с) император и дауншифтер Диоклетиан
В статье будет рассказано об одном из воплощений «Живого графа» — о клеточном автомате развёртывания графа GUCA (Graph Unfolding Cellular Automata). Демонстрацию работы GUСА можно «пощупать» прямо в браузере с подключённым Silverlight-плагином. Веб-приложение визуализирует короткую жизнь некоторых моих первых экземпляров растущих графов – как собственноручно сконструированных продуктов «генной инженерии», так и «естественно-отобранных» генетическим алгоритмом форм.
Даже если начальный граф будет состоять только из одного узла, а все порождающиеся узлы графа будут иметь одну и ту же копию набора правил с каждой новой итерации срабатывания правил можно будет наблюдать развитие самых разнообразных структур. Легко заметить, что начальный узел — аналогичен зародышу многоклеточного организма, остальные узлы графа аналогичны клеткам, наборы правил – хромосоме, а сами правила – генам.
Истоки
А всё началось с увлечения искусственными нейронными сетями (ИНС), при исследовании которых и родилась идея GUCA.
Небольшое напоминание. Искусственные нейронные сети, нашедшие широкое применения в искусственных же системах управления, можно представить как соединённые между собой «нейроны», сами по себе выполняющие достаточно простые операции, например, суммирование входящих сигналов и преобразование получившегося значения. Но будучи соединёнными по некоторым правилам в единую сеть «нейроны» образуют систему, возможности которой заметно превышают возможности cоставляющих её элементов — того же сумматора. Системе в целом уже доступны функции распознавания образов, классификации, фильтрации сигналов – всё то, что необходимо для построения сложной «интеллектуальной» системы управления.
На заре использования нейронных сетей топология сети задавалась исследователем, а параметры связей подбирались по наперёд заданному алгоритму, использующему накопленные данные о решаемой задаче. Если для достаточно простых типов нейронов задача построения топологии сети была достаточно детерминированной и решаемой (что не означает при этом решаемости самой задачи предметной области), то при использовании каскадов нейронных нелинейных динамических сетей с обратными связями, задача эта оказывалась не тривиальной и возникла идея поручить построение топологии нейронной сети компьютеру. На помощь пришли методы, подсмотренные в самой природе.
Речь идёт об нейроэволюционных методах,, в которых для построения топологий нейронных сетей используются генетические алгоритмы.
Нейро-эволюционные методы
Обзор таких методов был недавно опубликован на хабре: [1] habrahabr.ru/blogs/artificial_intelligence/84015,
Я не буду пересказывать уже известные способы реализации таких алгоритмов, напомню лишь основные положения косвенного кодирования сетей/графов, также лежащие в основе рассматриваемого метода GUCA, реализацию которого отличает лишь локальность, контекстный выбор применяемых правил и «запрограммированная смерть».
В косвенных методах кодирования нейронных сетей, в «геноме» экземпляра сети топология задаётся не явным перечислением узлов и связей, а косвенно через правила построения сети из небольшого её фрагмента. Ведь именно таким способом развивается организм животного из маленького зародыша, да и человеческий мозг.
Напомню также, что генетический алгоритм обеспечивает: случайную генерацию или модификацию кодов, оценку «результата» декодирования «генома» (т.е. оценку получившейся нейронной сети с помощью фитнесс-функции) и отбор лучших представителей.
Для нейронных систем выполняющих роль систем управления объектами (роботами, манипуляторами), фитнесс-функцией может стать работоспособность объекта управления в некой среде (лабиринте, при обращение с предметами, в полёте, в бою и т.п)
При этом косвенные способы кодирования обеспечивают следующие свойства:
1) Модульность. Рекурсивное построение фрактальных структур по простым правилам и повторение в конструкции организма неких стандартных блоков, элементов.
2) Полнота. Для любого заданной сети (графа) можно подобрать код.
3) Избыточность. Код может содержать избыточные данные никак не влияющие на результат декодирования
4) (При условии использования в правилах кодирования контекста)
a. Порождение топологии в зависимости от проходящих в нейронной сети сигналов
b. Регенерация — восстанавливаемость при локальных повреждениях
Из обзора [1] видно, что основные усилия исследователей направлены на изобретение более-менее удачных способов кодирования именно топологии сети, нежели на конструирование принципов работы нейрона/сети и кодирование её параметров, что не удивительно – ведь именно топология и определяет работу всей системы «нейронная сеть».
Выращивание топологии
Действительно, было бы полезно выделить в отдельную задачу проблему «выращивание» топологии сети с применением всё того же генетического алгоритма и косвенного кодирования (по сути – направленного графа, а ещё более абстрагируясь от НС – ненаправленного графа). Фитнесс-функцией (определяющей успешность выживания экземпляра) будет уже не способность нейронной сети справится с управляемым объектов, а, например, геометрические свойства топологии. Если же развернуть граф на плоскости или в пространстве — то оценкой приспособленности графа могут быть свойства получившегося изображения, в т.ч. растрового.
Концентрация усилий на более узкой задаче (построение топологий, абстрагируясь от нейронной сети) позволит:
• Найти более широкое применение в областях отличных от ИНС (автосборка механизмов, конфигурация распределённых вычислений в компьютерной сети или вирусов, взаимодействие боевых роботов).
• Наглядно представить результат (не только конечный, но и промежуточный) для исследователя, что может помочь при отработке алгоритмов лучше понимать причинно-следственные связи. К тому же, наглядное представление может подсказать идеи/решения/тупики.
• Объективней сравнивать различные решения по кодированию топологии или комбинировать удачные решения по кодированию топологии с различными конструкциями «нейронов». Объективно – т.е. независимо от конкретной предметной области применения.
• Проще (быстрее и дешевле) рассчитывать фитнес-функции (по сравнению с оценкой пригодности нейронной сети в качестве системы управления) – т.е. исследовать именно топологические алгоритмы, не затрачивая дополнительные ресурсы, в том числе и вычислительные, на производные задачи.
При этом, такие любопытные свойства как вышеперечисленные «модульность», «регенерация» — останутся доступными для исследования.
Можно добавить, что эволюция мозга животных также берёт начало от результата, достигнутого эволюцией формы многоклеточного организма (осе симметричность — хрящ – позвоночник — спинной мозг – несимметричность — головное уплотнение мозга).
Одним из таких методов и является клеточный автомат развёртывания графа GUCA, принципы работы которого будут изложены в следующем разделе.
Клеточный автомат развёртывания графа GUCA (Graph Unfolding Cellular Automata)
«Живой граф» GUCA – это конечный клеточный автомат, в котором каждый узел находится в одном из состояний (количество состояний конечно), и может переходить в другое состояние по определённым правилам, зависящим как от состояния самого узла, так и от его окружения. Эти правила едины для всех узлов, неизменны во времени и отрабатываются синхронно для всех узлов одновременно.
Классический представитель клеточного автомата – игра «Жизнь». Основное отличие «Живых графов» от классической игры «Жизнь» и её вариаций заключается в том что «внутриклеточные» автоматы расположены не на прямоугольной плоскости, а находятся в узлах графа с переменным количеством связанных соседей.
При этом, в отличии от большинства методов кодирования топологии сети описанных в обзоре [1], «Живой граф» GUCA исповедует следующие принципы:
• Контекстный выбор применяемых правил
• Только локальные и одношаговые изменения
• Не только рождение, но и смерть
Как ни странно, все эти особенности изначально присущи и клеточному автомату «Жизнь», хотя и были выбраны в результате долгих поисков наборов правил и операций, решающих задачу
развёртывания графа наиболее просто и полно.
Впрочем, операция удаления предлагалась в одном из упражнении курса лекций [2]
Принципы
Итак, в «Живом графе» GUCA узел находится в одном из состояний. И есть правила, по которым при определённых условиях срабатывания производятся операции над графом.
Примером набора правил, которые удовлетворяют вышеописанным «метаправилам» для некоторого экземпляра «живого графа» может служить такой список:
1. «Если узел находится в состоянии А, то создать связанный узел в состоянии В»
2. «Если узел находиться в состоянии В, и количество связей меньше двух, то создать связанный узел в состоянии В»
3. «Если узел находится в состоянии В и предыдущее состояние было B, то перейти в состояние С»
4.…
Состояние – один из элементов конечного множества. Можно обозначать числом или буквой алфавита – А, B, С, D,….
Операции. Понятно, что над графами можно проводить самые разные операции – добавлять/разделять узлы, замещать узлы связанной группой, объединять узлы. Я остановился на четырёх примитивных операциях, которых, похоже, будет вполне достаточно для воспроизведения любой сколь угодно сложной структуры.
• Переход узла в состояние X (таким образом, состояние X – это операнд операции)
• Рождение нового узла, связанного с текущим. Состояние нового узла X
• Соединение узла с ближайшим не соединённым узлом, находящимся в состоянии X
• Отсоединение узла, находящегося в состоянии X
Теперь об условиях, диктующих совершение операции в правиле. Я не ограничился зависимости от текущего состояния узла и количеством связей между этим узлом и другими узлами. К этим условиям добавил зависимости от предыдущего состояния узла и зависимость от числа родителей/делений узла (ведь каждый узел, согласно списку операций, порождён одним и только одним узлом-родителем).
Условия:
• Узел находится в состоянии X
• Предыдущее состояние узла равно Y
• Количество связей узла – от С1 до С2
• Количество предков узла (от которых он родился) – от P1 до P2.
Последнее условие и счётчик количества делений узла (аналог теломеразы) введены, чтобы обеспечить остановку развития всего организма и/или отдельных его модулей.
Я также рассматривал операции «соединение узла со всеми узлами в состоянии X», «смерть узла» — но посчитал их избыточными. Подумываю также ввести операцию «сброс счётчика делений». Отмечу, что все операции локальны и «вертятся» вокруг узла (изменяют только узел или его ближайшее окружение).
Впрочем, возможно, читатель сможет найти более стройную систему правил.
Грамматика правил
Правила GUCA можно записать и в краткой форме, обозначив текущее состояние – буквой, предыдущее – буквой в скобках, количество соседей – символом «с» (от connections), количество родителей – «p» (от parents). Если предыдущее состояние игнорируется в условии, то в скобкам будем указывать прочерк. Разделим в записи правила операции от условий символом двоеточия, а возможные операции обозначим следующим образом:
• Операцию перехода в другое состояние X обозначим X
• Операцию рождения связанного узла Ч обозначим ++X
• Операцию соединения с узлом X обозначим +X
• Операцию отсоединения от узла X обозначим –X
Тогда, для некоторого экземпляра «живого графа» набор правил будет записан с помощью грамматики:
1. А(А),p=0 :++B
2. B(-), c <2 :++B
3. B(B) :C
4. A(A) :G
5. C(B), c=1 :G
6. G(G), c <5 :H
Если начальный узел графа будет в состоянии «А», то через 12 последовательных итераций применения правил, мы получим «Пальцастую гантельку»:

Рисунок Граф «Пальцастая гантелька» и условное отображение её карты генов.
Это самый первый граф, сконструированный мною несколько лет назад для отладки конечного автомата на графах. Он настолько прост и понятен, что упоминаю его лишь для того, чтобы отдать дань уважения первопроходцу. Правила заложенные в его «геноме» просты: из узла с начальным состоянием А рождается короткая ниточка, оканчивающаяся узлами (в состоянии G), для которых срабатывает правило: пока количество соседей меньше или равно пяти — создать нового соседа.
Здесь и далее, при отображении графа на плоскости и на условном отображении карты генов красным цветом обозначается состояние А, розовым – B, зелёным – С, малиновым — G.
Выключив ген №5 из «пальцастой гантельки» можно сотворить «уродца» — «рука обыкновенная»:

Если включить ген обратно, вторая «рука» вырастит обратно.
Таким образом, набор простых правил может определять топологию графа. Вообще говоря, топологию графа определяет не только набор правил и начальное состояние его узла(узлов), но и некоторые глобальные ограничения – например максимальное количество итерации или максимально возможное количество соединений узлов.
Проверка идеи
Одним из способов убедиться, что описанная выше система правил достаточна для построения графов любой топологии — является решение «контрольных задачек» на построение. Задумав ту или иную фигуру постараться придумать «ген», из которого она и родится. И если задуманную фигуру не удастся никаким образом сконструировать, то система правил вряд ли будет пригодна не только для выращивание графов, но и для построения сложной искусственной нейронной сети.
«Контрольные задачи» должны быть с одной стороны предельно простыми, с другой стороны «показательными» (прошу не путать со «зрелищными») для демонстрации качественных свойств и эффектов сложного живого организма — модульности, гибридизации, самовосстанавливаемости… причудливости, наконец. Такими примерами могут быть – простейшие фракталы, растущие изнутри фигуры, сетки с большим количеством ячеек и просто «дикорастущие» растения.
Некоторые из этих задач было крайне сложно (долго) и не надёжно (ответ часто не сходился) решать в уме или на бумаге, и чтобы провести эти первые эксперименты, пришлось вооружить себя «экспериментальной установкой».
Экспериментальная установка (Silverlight-приложение)
Такой экспериментальной установкой стало программное приложение, позволяющее отладить «генетический код» и машину воспроизведения. Кроме этого, с её помощью можно:
• наглядно представить процесс роста графа,
• наглядно отобразить цветную «карту» хромосомы и активность генов в процессе роста графа
• посмотреть к чему приведёт выключение того или иной гена или разрезание «живого графа».
Демонстрационная Silverlight версия «экспериментальной установки» доступна по адресу http://roma.goodok.ru/guca/GUCA_DemoSL.html

Рисунок Silverlight версия «Экспериментальной установка» по выращиванию графа позволяет наблюдать процесс развития графа, активность генов на карте хромосомы, «подрезать» ножом отдельные веточки.
Чтобы запустить разворачивания графа, нужно на правой «панели управления» выбрать из выпадающего списка пример (Select sample) и нажать на кнопку запуска («Start»).
В центральной области с чёрным фоном будет отображаться граф в процессе его роста из единственного узла-зародыша. Различные состояния узлов отображаются соответствующим цветом. Можно изменить масштаб и вид отображения или замедлить рост графа, чтобы рассмотреть детали процесса.
Можно не только наблюдать развитие и жизнь графа, но и вмешиваться в этот процесс, надрезая «скальпелем» (переключатель «Knife») или выключая тот или иной ген, выводя на свет «уродцев», добиваясь «летального исхода» или «раковой опухли»
Справа внизу условно отображается «карта» хромосомы («Genome») — каждый прямоугольник на ней соответствует «гену» (пункту правила). Опять же таки, цветом кодируются состояния узлов в условии правила, само правило и состояние узла в операнде правила. В процессе роста графа зелёной подсветкой отмечаются те гены, которые были активны во время очередной итерации исполнения правил.
Наведя мышкой на прямоугольник отдельного «гена», можно увидеть расшифровку кодируемого геном правила в виде текста, а нажав кнопку мыши, выключить (или включить обратно) выбранный ген.
В этой статье я не буду останавливаться на описании устройства «лабораторной установки», хотя сама по себе её «сборка» была весьма интересным занятием – кроме теории графов и дискретной математики, пригодились знания и опыт численного решения уравнений математической физики, геометрии и пр. К тому же сам её генетический «исходный» код сам по себе является результатом эволюции и содержит в себе наследие далёких предков – ведь первая версия и проектные решения были реализованы на Delphi 7.0. Можно даже сказать, это мой первый «Hellow World!» на платформе Silverlight|WPF. Отмечу лишь, использование библиотек QuickGraph (графы и алгоритмы) и AForge (генетический алгоритм).
Простейшие примеры
Итак, давайте посмотрим некоторые простейшие примеры «живых графов», демонстрирующие живые свойства. Некоторые из экземпляров (например, вышеупомянутая «пальцастая гантелька») были сконструированы только божественным для мира живых графов началом (т.е. Мной), другие — результат эволюции, а третьи являются генетически модифицированными продуктами.
«Волосатая окружность»

Это фигура – генетически модифицированный продукт! Сначала с помощью генетического алгоритма была получена бесконечно растущая изнутри окружность (фитнесс-функция при этом зависела только от топологических характеристик графа – обязательного наличия двух граней). Затем, был добавлен ещё один «ген» — «ген волос» (крайний справа на карте генов)
Запуская растущий изнутри «организм» можно наблюдать, как отдельные сегменты окружности появляются в результате циклического повторения операций вставки новых рёбер.
«Пальцастая окружность» (гибрид)
Если взять гены «пальцастой гантельки» и «волосатой окружности» и объединить их в одной хромосоме «зародыша», то из него вырастет гибрид, унаследовавший как свойства «пальцастости» гантельки, так и «округлые» свойства:

Рисунок Гибрид «пальцастой гантельки» и «волосатой окружности» имеет общие свойства
Обратите внимание, что часть генов «пальцастой гантельки» во время всего процесса развёртывания графа остаются неактивными (на карте генов активность генов отмечается зелёной подсветкой).
«Кусты»(Фракталы)
Простейший генетический код из двух «генов» создаёт сколь угодно большой по размерам граф». Если отрезать любую его ветку, то «куст» почти мгновенно восстановиться в прежних размерах и формах.

Рисунок Примитивный фрактал задаётся лишь парой генов
«Кокошник (прямоугольная сетка)»
Эта и следующие две странные фигуры – результат моих попыток сконструировать квадратную сетку в виде квадрата.

Рисунок «Кокошник» — разворачивание прямоугольной сетки
Изменяя пару генов, можно выращивать сколь угодно большую (и малую) сетку. Ножом можно делать дырки. Попробуйте выключить ген №13 «O(O):+L» и включить его после разворачивания.
«Странная фигура 1» и «Странная фигура 2»
«Странная фигура 1» — это моя ошибка. На самом деле целью было создание равносторонней квадратной сетки. Фигура изображена на самом первом в статье рисунке (Рисунок 1). Если же подрезать её отростки прямо на живом графе, то, выпустив взамен отрезанных новые отростки, фигура примет более размашистый вид:

Рисунок «Странная фигура» после обрезания
Странная фигура 2. Хромосома этой фигуры отличается от хромосомы «Странной фигуры 2» всего лишь одним геном, точнее даже частью гена (близкие родственники), а вот форма результата «декодирования» мало похоже на форму предыдущего экземпляра.

«Странная фигура 2» – близкий родственник «Странной фигуры 1» — отличается всего лишь одним геном
«Шестиугольник с отростками» (результат эволюции)
Чтобы получить 10 генов этой фигуры потребовались тысячи итераций генетического алгоритма. Фитнесс функция в переводе на русский звучала примерно так: «чем ближе количество граней к двум, и число узлов степени 1 к шести и число узлов степени 3 к шести и число генов к нулю – тем больше шансов выжить у графа»(степень узла – количество связей)
Эволюция этого вида пережила несколько скачков: треугольник, квадрат с отростками, шести угольник с неправильными отростками, и, наконец, правильный. Замедлив процесс разворачивания, можно увидеть, какое решение нашла эволюция для построения фигуры.

Рисунок Шестиугольник с «листьями» — Результат работы генетического алгоритма
Заключение
Итак, мы увидели как с помощью таких абстрактных объектов как конечные автоматы и графы, можно создавать системы, забавным образом похожие на многоклеточные живые организмы, что демонстрирует общность принципов лежащих в основе «живых графов» и в законах образования геометрических форм живого.
Однако это не означает, что мы раскрыли тайны жизни. Это просто означает, что можно двигаться дальше: исследовать закономерности эволюций «живых графов». Напомню, что в демонстрационном приложении мы наблюдали «онтогенез» и результат эволюции, а не саму эволюцию.
Вопросами последующих исследований могут быть как определение границ модели «живых графов», так и поиск количественных и качественных закономерностей в неотягощённой излишними подробностями эволюционной модели (зависимость длин гена от сложности форм, статистики генетической информации от положения вида в дереве эволюции, скорости эволюции от набора допустимых операций и т.п.).
По результатам этих исследований, определив наиболее эффективные эволюционные алгоритмы, можно попробовать применить «живые графы» в исходной области: в искусственных нейронных сетях или в исследовании эволюции роботов, «аниматов», искусственных систем управления. Особый интерес представляет комбинация динамических нелинейных нейронных сетей с живыми графами, в которой состояние возбуждённости нейрона является одним из состояний конечного автомата «внутри» живого графа. Можно будет наблюдать что-то вроде «генетической памяти».
Также, было бы любопытно создать материальное воплощение живых графов в виде самоорганизующейся колонии примитивных роботов, в прошивку которых зашит генетический код сообщества.
Все эти направления трудно охватить исследователю-одиночке, и я надеюсь, некоторые из читателей ещё совершат свои маленькие и большие открытия в этой области исследований. Вполне возможно, модели подобные «Живым графам» станут отправной точкой для ваших собственных исследований. Правда, для этого понадобятся уже другие «экспериментальные установки».
Литература
[1] «Обзор методов эволюции нейронных сетей» http://habrahabr.ru/blogs/artificial_intelligence/84015/
[2] «Evolutionary Computation for Modeling and Optimization» Daniel Ashlock, January 12, 2004 http://orion.math.iastate.edu/danwell/ma378/
UPDATE Добавил возможность загрузить «геном» из xml. Пример файла: геном «странной фигуры 1». Теперь вы можете попробовать вырастить свои графы, проверить свои задумки… найти ошибки, наконец.
UPDATE 2 Выложил исходники (1.8Мб) с релизной сборкой.