Введение
Как-то стояла задача отсортировать уникальный массив строк с использованием GPU с минимум кода и максимально возможной скоростью…
В данном посте опишу основную идею ее решения. В качестве элементов массива сортировки в данном посте выступают числа.
Случай с уникальными элементами небольшого массива
В качестве платформы была выбрана CUDA по причинам, которые можно считать брэндовыми или индвидуальными. По факту, здесь много примеров именно на CUDA, и она на данный момент получила большее развитие в GPU-вычислениях, чем аналогичные платформы от ATI и OpenCL.
Поиск в сети по алгоритмам сортировки на CUDA дал разные результаты. Вот наиболее интересный. Там есть рисунок
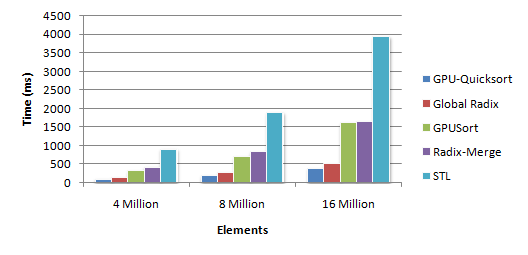
, из которого видно, что наилучший результат дал алгоритм QSORT, который дает сложность порядка от O(NlogN) до O(N^2). И хотя распараллеливание на GPU дало лучший в статье результат, закралось сомнение, что QSORT — не лучший способ использовать ресурсы видеокарты для данной задачи (особенно испугал размер приведенного кода). Далее описывается решение задачи, по сути «в одну строчку» ссложностью временной сложностью O(N) в худшем случае.
Итак, что имеем: современные видеокарты имеют более 500*32 потоков (GTX275), работающих одновременно, около 15000.
Условия задачи сортировки у меня были следующие: массив длиной до 1000 элементов (далее рассматривается и общий случай с большим значением, но у меня было так). Сортировать такой массив с O(NlogN) временем, имея 15000 потоков показалось как-то расточительно.
В результате папирусных рассуждений было установлено, что, для достижения наилучшей скорости, а это O(N) необходимо, чтобы каждый поток работая одновременно совершал не более O(N) операций. То есть один раз проходил по нашему массиву. А результатом прохода должен быть ключ, определяющий положение одного элемента в результирующем отсортированном массиве.
Зная собственный номер потока tid (как правило из 0..MaxThreads-1) была использована идея нахождения позиции tid-ого элемента в результате.
Принимая исходный массив за A[] = {1,5,2,4,7}, задаем задачу каждому потоку — найти положение элемента A[tid] в результирующем массиве B[].
Для этого заведем вспомогательный массив K[] — позиция элемента A[tid] в результате. ArraySize — количество элементов в A[].
Теперь самисходный код фрагмент реализации предлагаемого алгоритма на CUDA\C (файла .cu):
И все, результирующий массив B[] — отсортирован за O(N) при условии что имеющееся количество потоков больше или равно N.
Случай с уникальными элементами большого массива
Теперь, если увеличить размерность массива, можно использовать тот же подход, только один поток будет искать позиции
для [ArraySize/MaxThreads] — (целая часть от деления) элементов. В таком случае время работы алгоритма изменится на [ArraySize/MaxThreads]*O(N), то есть станет больше во столько раз, во сколько количество элементов массива больше имеющегося количества потоков.
Для такого случая реализация алгоритма примет вид:
Вывод 1
Обещанный итоговый алгоритм сортировки для одного потока с номером tid, записанный в одну строчку:
Было: A[i] — неотсортированный массив. Теперь K[tid] — содержит индексы позиций исходных элементов в результате. Порядок сортировки легко менять выбирая между B[K[tid]] = A[tid] и B[ArraySize-K[tid]-1] = A[tid].
Пример с данными из начала
Было: A[] = {1,5,2,4,7}. ArraySize = 5. Потоков запускаем 5.
Поток 0. tid = 0. Выставляем K[tid]=K[0] для A[tid]=A[0]=1: K[0] = 0
Поток 1. tid = 1. Выставляем K[tid]=K[1] для A[tid]=A[1]=5: K[1] = 3
Поток 2. tid = 2. A[2]=2. K[2]=1
Поток 3. tid = 3. A[3]=4. K[3]=2
Поток 4. tid = 4. A[4]=7. K[4]=4
Все. Теперь так как все потоки выполнялись одноременно то мы потратили время только на перебор массива — O(N). И получили K[] = {0,3,1,2,4}.
Особенности
Когда [ArraySize/MaxThreads]значительно больше>> ArraySize данный алгоритм принимает сложность большую, чем O(N^2).
Также не рекомендую его использовать когда заранее не известно, уникальны ли элементы исходного массива.
Выводы 2
Таким образом, исходная задача была решена за O(N) в худшем и O(N) лучшем случаях (ускорение было только за счет N потоков конечно). И то при условии, что имеющееся количество потоков не меньше количества элементов сортируемого массива.
Данный пост должен помочь начинающим исследователям алгоритмов в написании интересных идейных решений быстрых вычислений на GPGPU. Из литературы отмечу книгу алгоритмов Кормена и портал интересных задач projecteuler.net.
UPD1.(17.12.2010 13:40)
В процессе выяснилось, что если исходный массив A[] занимает 16КБ памяти, то еще хранить и результат B[] не получится в __shared__ памяти (а мы ее используем в CUDA как кэш 2-го уровня для ускорения вычислений) — т.к. __shared__ размером всего 16КБ (для GTX275).
Поэтому алгоритм дополнен «параллельным swap-ом», где результатом является исходный A[]:
Теперь исходный массив A[] стал отсортирован с использованием меньшего количества памяти.
UPD2.(17.12.2010 16:34, с учетом)
Более быстрый вариант за счет меньшего обращения к __shared__ памяти и небольшим оптимизациям.
UPD3.(20.12.2010 14:16) Предоставляю исходные коды примера: main.cpp, kernel.cu (размеры массива должны быть в пределах __shared__ памяти видеокарты).
UPD4.(23.12.2010 14:56) Насчет сложности O(N): предложенный алгоритм является разновидностью алгоритма сортировки подсчетом, имеющим линейную временную трудоёмкость Θ(n + k) © Wiki.
Как-то стояла задача отсортировать уникальный массив строк с использованием GPU с минимум кода и максимально возможной скоростью…
В данном посте опишу основную идею ее решения. В качестве элементов массива сортировки в данном посте выступают числа.
Случай с уникальными элементами небольшого массива
В качестве платформы была выбрана CUDA по причинам, которые можно считать брэндовыми или индвидуальными. По факту, здесь много примеров именно на CUDA, и она на данный момент получила большее развитие в GPU-вычислениях, чем аналогичные платформы от ATI и OpenCL.
Поиск в сети по алгоритмам сортировки на CUDA дал разные результаты. Вот наиболее интересный. Там есть рисунок

, из которого видно, что наилучший результат дал алгоритм QSORT, который дает сложность порядка от O(NlogN) до O(N^2). И хотя распараллеливание на GPU дало лучший в статье результат, закралось сомнение, что QSORT — не лучший способ использовать ресурсы видеокарты для данной задачи (особенно испугал размер приведенного кода). Далее описывается решение задачи, по сути «в одну строчку» с
Итак, что имеем: современные видеокарты имеют более 500*32 потоков (GTX275), работающих одновременно, около 15000.
Условия задачи сортировки у меня были следующие: массив длиной до 1000 элементов (далее рассматривается и общий случай с большим значением, но у меня было так). Сортировать такой массив с O(NlogN) временем, имея 15000 потоков показалось как-то расточительно.
В результате папирусных рассуждений было установлено, что, для достижения наилучшей скорости, а это O(N) необходимо, чтобы каждый поток работая одновременно совершал не более O(N) операций. То есть один раз проходил по нашему массиву. А результатом прохода должен быть ключ, определяющий положение одного элемента в результирующем отсортированном массиве.
Зная собственный номер потока tid (как правило из 0..MaxThreads-1) была использована идея нахождения позиции tid-ого элемента в результате.
Принимая исходный массив за A[] = {1,5,2,4,7}, задаем задачу каждому потоку — найти положение элемента A[tid] в результирующем массиве B[].
Для этого заведем вспомогательный массив K[] — позиция элемента A[tid] в результате. ArraySize — количество элементов в A[].
Теперь сам
1. Запускаем MainKernel (из kernel.cu) на ArraySize потоков.
MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);
2. В CUDA-ядро MainKernel (из kernel.cu) приходит A[], ArraySize, MaxThreads, выходит B[] и K[].
unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //получаем текущий номер потока
for (unsigned long i = 0;i<ArraySize;++i) //основной цикл O(N)
if (A[i]<A[tid])
++K[tid]; //определяем позицию текущего элемента в результате O(1)
3. __syncthreads(); //синхронизируем потоки до текущего момента можно и без этой строчки, т.к. результат tid-ой позиции не зависит от соседнего элемента
4. B[K[tid]] = A[tid]; //помещаем элемент в его позицию (за O(1), одно действие а не 3 и более как в qsort, swap и т.д.)
*В моем случае сортируемые значения были уникальные, потому здесь нет проверки ситуации когда K[]={0,0,2,3,4}.
Такой случай незначительно усложняет п.4 следующего примера реализации, отличающегося еще одним массивом индексного смещения (также O(1)). Оставляю его реализацию на выбор читателей. И все, результирующий массив B[] — отсортирован за O(N) при условии что имеющееся количество потоков больше или равно N.
Случай с уникальными элементами большого массива
Теперь, если увеличить размерность массива, можно использовать тот же подход, только один поток будет искать позиции
для [ArraySize/MaxThreads] — (целая часть от деления) элементов. В таком случае время работы алгоритма изменится на [ArraySize/MaxThreads]*O(N), то есть станет больше во столько раз, во сколько количество элементов массива больше имеющегося количества потоков.
Для такого случая реализация алгоритма примет вид:
1. Запускаем MainKernel (из kernel.cu) на [ArraySize/MaxThreads] потоков.
MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);
2. В CUDA-ядро MainKernel (из kernel.cu) приходит A[], ArraySize, MaxThreads, выходит B[] и K[].
unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //получаем текущий номер потока
2.5. Здесь перебираем элементы массива, которые должен проверить текущий поток.
unsigned long c = ArraySize/MaxThreads;
for (unsigned long j = 0;j<c;++j) {
unsigned int ttid = c*tid + j; //обновленный номер текущего элемента - с учетом многопроходности для одного потока
for (unsigned long i = 0;i<ArraySize;++i)
if (A[i]<A[ttid])
++K[ttid]; //позиция в результате
3. __syncthreads(); //синхронизируем потоки до текущего момента можно и без этой строчки, т.к. результат tid-ой позиции не зависит от соседнего элемента
4. B[K[ttid]] = A[ttid]; //помещаем элемент в его позицию
} //конец цикла многопроходностиВывод 1
Обещанный итоговый алгоритм сортировки для одного потока с номером tid, записанный в одну строчку:
for (unsigned long i = 0;i<ArraySize;++i) if (A[i]<A[tid]) ++K[tid];Было: A[i] — неотсортированный массив. Теперь K[tid] — содержит индексы позиций исходных элементов в результате. Порядок сортировки легко менять выбирая между B[K[tid]] = A[tid] и B[ArraySize-K[tid]-1] = A[tid].
Пример с данными из начала
Было: A[] = {1,5,2,4,7}. ArraySize = 5. Потоков запускаем 5.
Поток 0. tid = 0. Выставляем K[tid]=K[0] для A[tid]=A[0]=1: K[0] = 0
Поток 1. tid = 1. Выставляем K[tid]=K[1] для A[tid]=A[1]=5: K[1] = 3
Поток 2. tid = 2. A[2]=2. K[2]=1
Поток 3. tid = 3. A[3]=4. K[3]=2
Поток 4. tid = 4. A[4]=7. K[4]=4
Все. Теперь так как все потоки выполнялись одноременно то мы потратили время только на перебор массива — O(N). И получили K[] = {0,3,1,2,4}.
Особенности
Когда [ArraySize/MaxThreads]
Также не рекомендую его использовать когда заранее не известно, уникальны ли элементы исходного массива.
Выводы 2
Таким образом, исходная задача была решена за O(N) в худшем и O(N) лучшем случаях (ускорение было только за счет N потоков конечно). И то при условии, что имеющееся количество потоков не меньше количества элементов сортируемого массива.
Данный пост должен помочь начинающим исследователям алгоритмов в написании интересных идейных решений быстрых вычислений на GPGPU. Из литературы отмечу книгу алгоритмов Кормена и портал интересных задач projecteuler.net.
UPD1.(17.12.2010 13:40)
В процессе выяснилось, что если исходный массив A[] занимает 16КБ памяти, то еще хранить и результат B[] не получится в __shared__ памяти (а мы ее используем в CUDA как кэш 2-го уровня для ускорения вычислений) — т.к. __shared__ размером всего 16КБ (для GTX275).
Поэтому алгоритм дополнен «параллельным swap-ом», где результатом является исходный A[]:
1. for (unsigned long i = 0;i<ArraySize;i++)
if (A[i]<A[tid])
K[tid]++; //позиция в результате
2. __syncthreads(); //обязательная синхронизация!
3. unsigned long B_tid = A[tid]; //элемент, "закрепленный" за текущим потоком
4. __syncthreads(); //убеждаемся что все потоки разобрали "свои" элементы
5. A[K[tid]] = B_tid; //ставим элемент в его местоТеперь исходный массив A[] стал отсортирован с использованием меньшего количества памяти.
UPD2.(17.12.2010 16:34, с учетом)
Более быстрый вариант за счет меньшего обращения к __shared__ памяти и небольшим оптимизациям.
0. unsigned int K_tid = 0;
1. unsigned long B_tid = A[tid]; //элемент, "закрепленный" за текущим потоком
2. for (unsigned long i = 0;i<ArraySize;++i)
if (A[i]<B_tid)
++K_tid; //позиция в результате
3. __syncthreads(); //убеждаемся что все потоки разобрали "свои" элементы
4. A[K_tid] = B_tid; //ставим элемент в его местоUPD3.(20.12.2010 14:16) Предоставляю исходные коды примера: main.cpp, kernel.cu (размеры массива должны быть в пределах __shared__ памяти видеокарты).
UPD4.(23.12.2010 14:56) Насчет сложности O(N): предложенный алгоритм является разновидностью алгоритма сортировки подсчетом, имеющим линейную временную трудоёмкость Θ(n + k) © Wiki.